Ильичев В.Г. Устойчивость, адаптация и управление в экологических системах
Подождите немного. Документ загружается.

188
этом случае собственные экономические интересы каждого «рыбака» не позволят
им уклониться от кооперативных стратегий (хотя они могут и не подозревать об
этом!).
Формализация этой идеи заключается в следующем. Пусть заданы
(
)
wq
и
- функции полезности «рыбаков». Напомним, что они строго вогнутые и
непрерывно дифференцируемы:
()
vr
(
)
00
=
q
,
(
)
00
=
r и
(
)()
10'0' =
=
rq
. При заданном
начальном запасе рыбы в водоеме доход
()
x
(
)
xB от кооперативной эксплуатации
популяции за бесконечное время задается выражением
(3.2)
() (){
⎥
⎦
⎤
⎢
⎣
⎡
+
∑
∞
=0
sup
t
t
tt
vrwq
β
}
по всем допустимым
{}
и
t
w
{
}
t
v . Данная целевая функция сводится к
рассмотренной раннее (1.5), если ввести функцию полезности
(
)
(
)
(
)
[
]
vrwqup
+
=
max
(3.3)
по всем ,
0≥w 0≥
v
,
uvw
≤
+
. Нетрудно показать, что
p
строго возрастает и
строго вогнута: и
()
00 =p
(
)
10'
=
p
. В силу раздела 7.1, функция непрерывно
дифференцируема, строго возрастает и строго вогнута.
()
xB
Обозначим и
()
xww =
(
)
xvv
=
- оптимальные управления в задаче (3.1) +
(3.2). Из (3.3) следует: или
(
)
vw, одновременно равны нулю, или
(
)
vw,
одновременно положительны. Имеет место следующий аналог утверждения 2.1.
Утверждение 3.1. Для одновременно положительных управлений
выполняются соотношения
()
(
)
1''
<
= wqxB
и
(
)
(
)
1'' <
=
vrxB
(3.4)
Обратно, если имеют место соотношения (3.4) то и
w
v
- положительные
оптимальные управления в точке х.
Пусть теперь задана внутренняя цена
(
)
xB' для всех
x
. Тогда будем считать,
что каждый рыбак в интервале
(
)
1,
+
tt должен выплачивать налог
(
)
xB' за
189
каждую единицу выловленной рыбы. Значит, локальные задачи «рыбаков» имеют
вид (индексы
t
у всех переменных для краткости опущен):
1)
(
)
(
)
[
]
xwBwq 'max
−
по всем из w
[
]
x,0
;
2)
(
)
(
)
[
]
xvBvr 'max
−
по всем
v
из
[
]
x,0
.
Утверждение 3.2. Решения в локальных задачах совпадают с оптимальными
управлениями в глобальной задаче (3.1) + (3.2).
Таким образом, с помощью внутренних цен решение сложной динамической
задачи управления допускает расщепление на две простые статические
оптимизационные задачи.
Представляет интерес задача о связи деформации функций полезности и
воспроизводства с соответствующей внутренней ценой.
В работе (Рохлин, 2000) получено довольно полное решение данной
проблемы. Приведем основные результаты. Пусть - две разные функции
полезности. При фиксированной функции воспроизводства обозначим через -
соответствующие функции Беллмана. Имеет место
qp,
BA,
Утверждение 3.3. Пусть для всех , тогда
для всех .
)()(
//
uqup <
0>u
)()(
//
xBxA <
0>x
Иными словами, сильный рост спроса на рыбу вызывает рост внутренней
цены. В частности, увеличение количества рыбаков сопровождается повышением
внутренней цены эксплуатируемой популяции.
Взаимосвязь деформации функции воспроизводства и соответствующей
внутренней цены оказывается не столь однозначной.
Пусть - две разные функции воспроизводства. При фиксированной
функции полезности обозначим через - соответствующие функции Беллмана.
На основе схемы обоснования предыдущей теоремы можно установить
GF,
BA,
Утверждение 3.4. Пусть и , тогда
для всех .
)()(
//
xGxF ≤
)()( xGxF >
)()(
//
xBxA <
0>x
190
В частности, дополнительное поступление (=увеличение предложения) рыбы
в водоем вызывает уменьшение ее внутренней цены.
Разнообразные компьютерные эксперименты позволяют во многих случаях
(но не во всех!) руководствоваться следующим эвристическим «эколого-
экономическим» принципом.
Гипотеза Э. Увеличение спроса на рыбу вызывает рост ее внутренней цены.
Напротив, увеличение предложения рыбы уменьшает ее внутреннюю цену.
Представляет интерес выяснение условий, при которых справедлив
указанный принцип.
Концепция внутренней цены эффективна и в более сложных ситуациях,
когда облавливается несколько популяций из сообщества. Так, пусть первый
«рыбак» облавливает популяцию
x
, а второй – популяцию . Данные популяции
могут оказаться взаимодействующими (конкуренты, «хищник-жертва» и т.д.),
тогда их динамика с учетом вылова задается системой
y
(
)
ttttt
vywxFx
−
−
=
+
,
1
, (3.5)
(
)
ttttt
vywxGy
−
−
=
+
,
1
,
где и . Обозначим
tt
xw ≤≤0
tt
yw ≤≤0
(
)
wq
и
(
)
vr (возрастающие и вогнутые
соответственно) функции полезности рыбаков. Как и ранее, возникает конфликтная
ситуация между «рыбаками» (кому и сколько ловить). Наиболее привлекательная
социально-экономическая ситуация возникает, когда рыбаки действуют
кооперативным образом. В этом случае целевая функция имеет вид
() (){
⎥
⎦
⎤
⎢
⎣
⎡
+
∑
∞
=0
sup
t
t
tt
vrwq
β
}
(3.6)
по всем допустимым
{}
и
t
w
{
}
t
v . При естественных и достаточно общих
ограничениях на функции воспроизводства
F
и
G
можно утверждать: для задачи
(3.5) + (3.6) существует единственная непрерывная функция Беллмана
(
)
yxB ,
- это
максимально возможный доход то эксплуатации взаимодействующих популяций,
191
когда их начальные численности равны х и у. Самое главное, оказывается
монотонно возрастающей ( как по х, так и по у) функцией. В силу монотонности,
обе частные производные
(
yxB ,
)
(
)
yxB ,
существуют почти для почти всех пар
(
)
yx,
,
Используя схему вывода формулы (2.1), для оптимального управления
устанавливаем следующее:
1) пусть , тогда почти для всех
()
0, ≥= yxww
(
)
yx,
(
)
(
)
wqxyxB '/,
=
∂
∂
(3.7)
И обратно, если удовлетворяет (3.7), то - оптимальный вылов;
w w
2) пусть
()
0, >
=
yxvv
, тогда почти при всех
(
)
yx,
()
(
)
vryyxB '/,
=
∂
∂
(3.8)
И обратно, если
v
удовлетворяет (3.8), то
v
- оптимальный вылов.
Здесь будем называть
xBc
x
∂
∂
=
/ ,
yBc
y
∂
∂
=
/
внутренними ценами
популяций х и у соответственно. Пусть задано состояние
(
)
yx,
, тогда для каждого
из рыбаков возникает своя локальная задача – максимизация ежегодной
индивидуальной прибыли:
1)
(
)
[
]
x
wcwq
−
max по всем из w
[
]
x,0
;
2)
(
)
[
]
y
vcvr
−
max
по всем
v
из
[
]
y,0
.
Из формул (3.7) и (3.8) следует: почти для всех пар
(
)
yx,
управления в локальных
задачах совпадают с оптимальными управлениями в глобальной задаче (3.5) + (3.6).
Теоретически существует функция Беллмана и для всей эксплуатируемой
экосистемы. Разумеется, практически построить такую функцию весьма
затруднительно.
7.4. Изменение внутренней цены при адаптации
эксплуатируемой популяции
192
Естественный отбор осуществляется при конкурентном взаимодействии
близких популяций. «Близость» означает, что популяции оказывают одинаковое
конкурентное давление на скорость роста. В главе 4 было показано, что динамика
двух близких популяций описывается системой
()
tttt
yxfxx
+
=
+1
и
()
tttt
yxgyy +
=
+1
, (4.1)
где и - убывающие функции роста. Будем считать, что и
)(zf )(zg
()
zzf
(
)
zzg
-
монотонно возрастающие и вогнутые функции воспроизводства. Очевидно: если
для всех
() ()
zgzf >
z
, то
x
- «сильная» популяция и вытесняет «слабую»
популяцию . Представляет интерес проблема о влиянии оптимальной
эксплуатации (одного рыбака) на исход конкуренции двух близких популяций
y
()
(
)
tttttt
uyxfwxx −+−=
+1
и
(
)
(
)
tttttt
uyxgvyy −
+
−
=
+1
, (4.2)
где , ,
tt
xw ≤≤0
tt
yv ≤≤0
ttt
vwu
+
=
. Рассмотрим два варианта оптимизации
вылова в предположении, что функции полезности рыб-конкурентов
q
p
=
.
Излагаемые ниже результаты (предположения 4.1 и 4.2) получены с помощью
компьютерного анализа и нуждаются в строгом обосновании.
1. Пусть поставка вылова производится на разные рынки (
w - на один
рынок, а
v
- на другой). Иными словами, «полезности» от и w
v
не влияют друг на
друга. Поэтому целевая функция задается выражением
() (){}
sup
0
→+
∑
∞
=
t
t
tt
vpwp
β
(4.3)
Предположение 4.1. В модели оптимальной эксплуатации (4.2) + (4.3)
«сильная» и «слабая» популяции сосуществуют.
Следовательно, такого сорта эксплуатация может затормозить ход
эволюционного процесса. Поскольку на сегодняшний день лишь отчасти известны
закономерности эволюционного процесса, то сильная деформация вектора
эволюции нежелательна. Одним из возможных вариантов допустимой деформации
является условие, чтобы соответствующие векторы эволюции составляли острый
угол (= эволюционно-устойчивое развитие эколого-экономических систем).
193
2. Обсудим другой вариант построения внутренних цен на рыбу, когда
поставка (
w и
v
) реализуется на одном и том же рынке. В этом случае и w
v
«конкурируют друг с другом». Учет этого обстоятельства произведем на основе
представления
(
)(
zzzp
)
ϕ
=
, где
(
)
z
ϕ
- рыночная цена единицы рыбной продукции
(см. разд. 6.1). Действительно, при поставке на рынок одновременно
(
)
vw
+
кг
рыбы рыночная цена единицы рыбы будет равна
(
)
vw
+
ϕ
, а доход от продажи
будет равен
()()
(
)
vwpvwvw
+
=++
ϕ
. Поэтому здесь целевая функция имеет вид
. (4.4)
()
sup
0
→+
∑
∞
=
t
t
tt
vwp
β
Предположение 4.2. В модели оптимальной эксплуатации (4.2)+(4.4)
«сильная» популяция вытесняет «слабую».
Теперь сохраняется естественный ход эволюционного процесса.
Рассмотрим в качестве примера следующую модельную схему динамики
отдельной популяции
(
)
tt
xrx +=
+
1ln
1
. (4.5)
Заметим, что в данном случае конкуренция двух близких популяций (с
разными и ) описывается моделью (4.1), в которой
1
r
2
r
()
(
)
zzrzf /1ln
1
+
=
и
(
)
(
)
zzrzg /1ln
2
+
=
.
Легко показать, что здесь популяции с большим параметром
r
имеют
конкурентное преимущество. Значит, в процессе эволюции будет происходить
увеличение параметра
r
.
Обозначим через функцию Беллмана для эксплуатируемой
популяции в рамках данной модельной схемы
(
rxB ,
)
(
)
ttt
uxrx −+=
+
1ln
1
. (4.6)
с целевой функцией (1.3). Любопытно выяснить, как изменяется внутренняя цена
с ростом
()
rxB
x
,'
r
. Заметим, что с экономической точки зрения рост данного
параметра
r
вызывает увеличение “предложения”. Согласно гипотезе Э
194
внутренняя цена должна уменьшиться. Однако численные расчеты показали, что
результат зависит от вида функции полезности.
При с ростом
)1ln()( uup +=
r
внутренняя цена неожиданно
возрастает для всех
),(
/
rxB
x
x
. Было бы заманчиво предположить, что в процессе эволюции
происходит рост внутренней цены, вызывающий снижение вылова.
Однако при
)1/()( uuup
+
=
рост
r
сопровождается увеличением внутренней
цены при малых
x
, а при больших
x
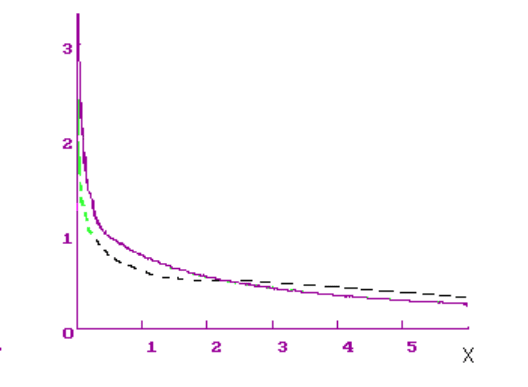
внутренняя цена убывает (см. рис. 7. 2).
Рис. 7. 2. Внутренняя цена при
)1/()( uuup
+
=
и разных
r
в функции
воспроизводства (4.6). Пунктир соответствует
5.1
=
r
, а сплошная - .
3=r
7.5. Сезонная внутренняя цена и эксплуатация водных ресурсов
Внутригодовая динамика популяции может зависеть от сезонных факторов
(температуры и т.д.), которые периодически повторяются. В этом случае модель
развития преобразуется к виду
),(
1
tuxFx
ttt
−
=
+
.
Аналогично, и функция полезности может зависеть от времени .
Тогда целевая функция имеет вид
)t,u(p
.
∑
∞
=
→
0
max),(
t
t
t
tup
β
Пусть в начальный момент времени
t
биомасса популяции равна x. Теперь
195
функция Беллмана B(x, t) зависит от двух аргументов. Если
t
- номер сезона, то B -
периодическая по целочисленному аргументу t с периодом 4.
Пусть при каждом t функции и
F
p
удовлетворяют прежним
ограничениям. Тогда функция B(x,t) является непрерывной, возрастающей и
вогнутой (по переменной x). Поэтому для почти всех x существует -
производная B (x, t) по первому аргументу. Если в некоторой точке x существует
, то для положительного оптимального управления выполняется ключевое
соотношение:
)t,x(B
/
x
)t,x(B
/
x
= .
),(
/
txB
x
),(
/
tup
u
Представляется естественным назвать - ценой единицы рыбной
популяции в t-й сезон при биомассе популяции равной x.
),(
/
txBc
xt
=
Отметим следующий любопытный аспект. Пусть в какой-то (“мертвый”)
сезон популяция не используется (=функция полезности равна нулю). Что можно
сказать про ее внутреннюю цену в “мертвый” сезон? В результате компьютерных
экспериментов установлено, что внутренняя цена в “мертвые” сезоны все-таки
положительна, но существенно меньше внутренней цены в “живые” сезоны.
Применим данный подход к оценки цены воды Цимлянского
водохранилища, объем которого равен 24 км
3
. Считаем, что элементы водного
баланса (приток, осадки, испарение) ежегодно повторяются и совпадают со
среднемноголетними данными (Знаменский, 1977). Согласно данным наибольший
приток приходится на весну, а наименьший – на лето.
В Цимлянском водохранилище основными потребителями являются: 1)
гидроэнергетика (требуется поддерживать достаточно большой сток из водоема в
течение всего года); 2) рыбное хозяйство (требуются весенние попуски из
водохранилища); 3) сельское хозяйство (требуются водозаборы весной и летом); 4)
речной транспорт Нижнего Дона (требуются летние попуски из водохранилища).
Построение фактической функции полезности для каждого из четырех
водопотребителей представляет собой серьезную и актуальную экономико -
статистическую проблему. В качестве иллюстрации возьмем одну и ту же
нелинейную зависимость, но с учетом сезонного водопотребления. Например, для
196
пользователя “рыбное хозяйство” полагаем )u1/(u)t,u(p
2
+
=
, если
t
- весна и
для остальных
0)t,u(p
2
=
t
.
Рассмотрим простейшую балансовую модель (Матишов, Ильичев, 2006):
,
)24,uuuuvxmin(x
4
t
3
t
2
t
1
ttt1t
−−−−+=
+
где - объем водоема, - результирующее действие элементов водного баланса,
- потребление воды - тым пользователем.
t
x
t
v
k
t
u
k
В качестве ограничения потребуем, чтобы при водопотреблении объем
водоема каждого месяца не опускался ниже величины 12 км
3
(=половина объема).
При малых данное ограничение не выполняется, в этом случае потребление
воды полагаем равным нулю.
t
x
На основе компьютерных расчетов построена (периодическая по
целочисленной переменной
t
) функция - максимально возможный доход
при кооперативном взаимодействии всех потребителей с учетом внутригодового
режима элементов водного баланса. В результате вычисления определена
внутренняя цена на воду Цимлянского водохранилища в зависимости от сезона
(при фиксированном объеме водоема). Установлен следующий порядок цен (от
самой дешевой до самой дорогой):
)t,x(B
)t,x(B
/
x
зима <осень < весна < лето.
Такое соотношение цен представляется вполне разумным.
Обсуждение. 1. Предложенный “нетрадиционный” подход к решению
динамической проблемы управления оказывается, на самом деле, продолжением
стандартных методов решения статических оптимизационных задач. Так,
напомним классическую постановку:
max)( →zF
при ресурсном ограничении .
bzG ≤)(
Пусть
)(b
ϕ
- соответствующее значение целевой функции. Тогда производная
считается ценой ресурса, когда его запасы равны . В проблеме вылова такой
функцией
)(
/
b
b
ϕ
b
ϕ
является функция Беллмана, а ограничением является численность
популяции.
197
2. Разрешимость уравнения Беллмана доказана с помощью принципа
сжимающих отображений, в котором дисконт
β
является коэффициентом сжатия.
Отметим, что теоремы существования встречаются на каждом шагу, надо только
быть внимательным. Вот одно из таких наблюдений (Ильичев, 1988б),
представленное в задаче М1100 журнала ”Квант”.
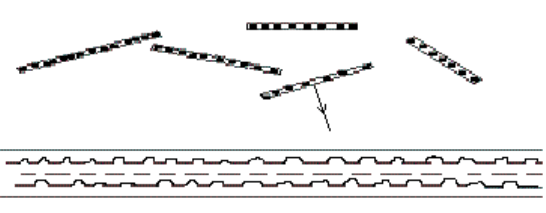
Теорема. Пусть на берегу реки лежит конечное число бревен. Каждое
бревно составляет с прямой линией берега угол меньше 45
0
(см. рис. 7.3). Тогда
найдется “хорошее” бревно, которое можно закатить в реку, не задевая
остальных.
Рис. 7. 3. “Хорошее” бревно (со стрелкой) среди “плохих”.
3. На основе развитого подхода возможны и другие постановки проблем
иерархического управления в системе ”рыбак - государство”. Так, весьма
любопытна задача: какая последовательность цен
{
}
t
c позволяет государству
получить максимальный многолетний доход от мягкого налогообложения.
Представляет интерес развить теорию жесткого налогообложения (2.4). В
частности, можно ли в рамках жесткой схемы налогообложения заставить рыбаков
– конкурентов действовать кооперативным образом?
Наряду с ценой представляется целесообразным использовать и другие
финансово - экономические инструменты: акции, опционы, фьючерсы и их
разновидности. Здесь следует иметь в виду, что теоретически корректные механизмы
могут совсем не годиться для практического использования. Так, приведем пример
практически бесполезного механизма. А именно, экологическую систему можно
