Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


EXAMPLE 3
Graph the equation without using a calculator.
153x
2
192xy 97y
2
1710x 1470y 5625 0.
SOLUTION The angle u and the rotation equations for eliminating the xy term
were found in the preceding example. Substitute the rotation equations in the
given equation.
153x
2
192xy 97y
2
1710x 1470y 5625 0
153
4
5
u
3
5
v
2
192
4
5
u
3
5
v
3
5
u
4
5
v
97
3
5
u
4
5
v
2
1710
4
5
u
3
5
v
1470
3
5
u
4
5
v
5625 0
153
1
2
6
5
u
2
2
2
4
5
uv
2
9
5
v
2
192
1
2
2
5
u
2
2
7
5
uv
1
2
2
5
v
2
97
2
9
5
u
2
2
2
4
5
uv
1
2
6
5
v
2
2250u 150v 5625 0
225u
2
25v
2
2250u 150v 5625 0
9u
2
v
2
90u 6v 225 0
9(u
2
10u) (v
2
6v) 225.
Finally, complete the square in u and v (adding the appropriate amounts to the
right side so as not to change the equation).
9(u
2
10u 25) (v
2
6v 9) 225 9
25 9
9(u 5)
2
(v 3)
2
9
(u
1
5)
2
(v
9
3)
2
1.
Therefore the graph is an ellipse centered at (5, 3) in the uv coordinate system, as
shown in Figure 10–57. ■
Figure 10–57
1
1
y
x
3
5
u
v
36.87°
726 CHAPTER 10 Analytic Geometry

SECTION 10.5 Plane Curves and Parametric Equations 727
EXERCISES 10.4.A
In Exercises 1–4, find the new coordinates of the point when
the coordinate axes are rotated through the given angle.
1. (3, 2); u 45° 2. (2, 4); u 60°
3. (1, 0); u 30° 4. (3, 3); sin u 5/13
In Exercises 5–8, rotate the axes through the given angle to
form the uv coordinate system. Express the given equation in
terms of the uv coordinate system.
5. u 45°; xy 1
6. u 45°; 13x
2
10xy 13y
2
72
7. u 30°; 7x
2
63
xy 13y
2
16 0
8. sin u 1/5
; x
2
4xy 4y
2
55
y 1 0
In Exercises 9–12, find the angle of rotation that will eliminate
the xy term of the equation and list the rotation equations in
this case.
9. 41x
2
24xy 34y
2
25 0
10. x
2
23
xy 3y
2
83
x 8y 32 0
11. 17x
2
48xy 31y
2
49 0
12. 52x
2
72xy 73y
2
200
THINKERS
13. (a) Given an equation
Ax
2
Bxy Cy
2
Dx Ey F 0, with B 0. and
an angle u, use the rotation equations in the box on
page 723 to rewrite the equation in the form
Au
2
Buv C v
2
Du Ev F0,
where A, . . . , F are expressions involving sin u, cos u,
and the constants A, . . . , F.
(b) Verify that B2(C A) sin u cos u B(cos
2
u sin
2
u).
(c) Use the double-angle identities to show that
B(C A) sin 2u B cos 2u.
(d) If u is chosen so that cot 2u (A C )/B, show that
B 0. This proves the statement in the box on
page 725.
14. Assume that the graph of Au
2
Cv
2
Du Ev F0
(with at least one of A, C nonzero) in the uv coordinate
system is a nondegenerate conic. Show that its graph is an
ellipse if AC0 (A and C have the same sign), a hyper-
bola if AC0 (A and C have opposite signs), or a
parabola if AC0.
15. Assume the graph of Ax
2
Bxy Cy
2
Dx Ey F 0
is a nondegenerate conic section. Prove the statement in the
box on page 720 as follows.
(a) In Exercise 13(a), show that (B)
2
4ACB
2
4AC.
(b) Assume that u has been chosen so that B0. Use
Exercise 14 to show that the graph of the original
equation is an ellipse if B
2
4AC 0, a parabola if
B
2
4AC 0, and a hyperbola if B
2
4AC 0.
10.5 Plane Curves and Parametric Equations*
■ Graph a curve given by parametric equations.
■ Express a parametric curve as part of the graph of an equation
in x and y.
■ Find a parametric representation for the graph of an equation in
x and y.
There are many curves in the plane that cannot be represented as the graph of a
function y f (x). Parametric graphing enables us to represent such curves in
terms of functions and also provides a formal definition of a curve in the plane.
Consider, for example, an object moving in the plane during a particular time
interval. To describe both the path of the object and its location at any particular
Section Objectives
*Parametric graphing was introduced in Special Topics 3.3.A, which is not a prerequisite for this section.
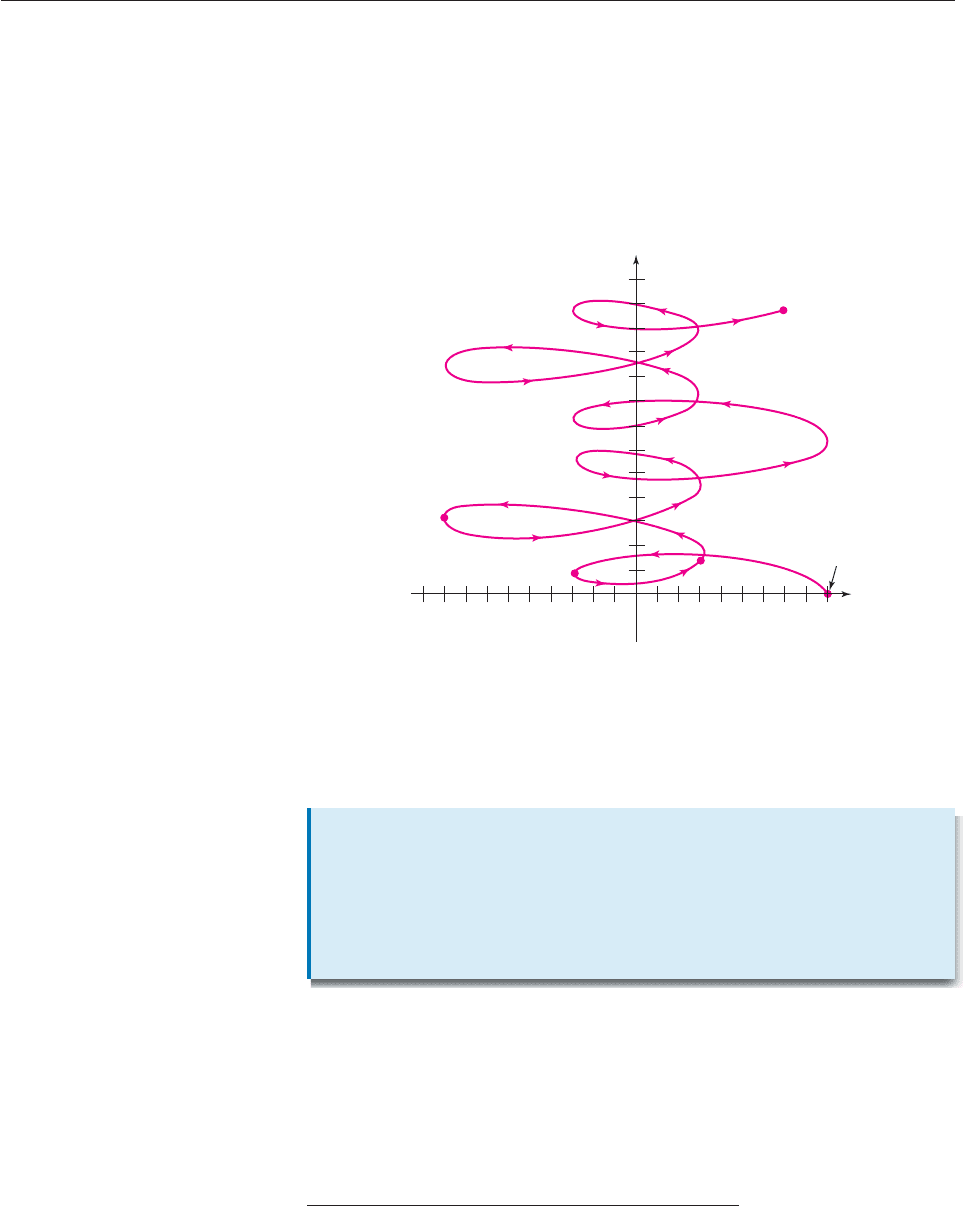
time, three variables are needed: the time t and the coordinates (x, y) of the object
at time t. For instance, the coordinates x and y might be given by
x 4 cos t 5 cos(3t) and y sin(3t) t.
From t 0 to t 12.5, the object traces out the curve shown in Figure 10–58. The
points marked on the graph show the location of the object at various times.
Note that the object may be at the same location at different times (the points
where the graph crosses itself).
Figure 10–58
In the preceding example, both x and y were determined by continuous func-
tions of t, with t taking values in the interval [0, 12.5].* The example suggests the
following definition.
In this general definition of “curve,” the variable t need not represent time. As the
following examples illustrate, different pairs of parametric equations may pro-
duce the same curve. Each such pair of parametric equations is called a parame-
terization of the curve.
A curve given by parametric equations can be graphed by hand, as in the next
example.
t = 1
t = 3
t = 2
t = 0
t = 12.5
–3 1–9 9
x
y
728 CHAPTER 10 Analytic Geometry
*Intuitively, “continuous” means that the graph of the function that determines x, namely,
f (t) 4 cos t 5 cos 3t, is a connected curve with no gaps or holes and similarly for the function that
determines y. Continuous functions are defined more precisely in Chapter 13.
Definition of
Plane Curve
Let f and g be continuous functions of t on an interval I. The set of all points
(x, y) where
x f (t) and y g(t)
is called a plane curve. The variable t is called a parameter, and the equa-
tions defining x and y are parametric equations.

EXAMPLE 1
Sketch the graph of the curve whose parametric equations are
x t
3
1 and y 2t (2 t 2).
SOLUTION We choose values of t between 2 and 2, and compute the corre-
sponding values of x and y.
Next we plot the points (x, y) given by the table: (7, 4), (2.375, 3), (0, 2),
etc. (Figure 10–59). The plotted points suggest the graph in Figure 10–60. ■
Figure 10–59 Figure 10–60
Graphing more complicated curves is difficult to do by hand, but quite easy
when technology is used. For example, to graph the curve shown in Figure 10–58,
which is given by the parametric equations
x 4 cos t 5 cos(3t) and y sin(3t) t,
put your calculator or computer in parametric graphing mode. Then enter the
equations (Figure 10–61) and the viewing window, as partially shown in Fig-
ure 10–62 (scroll down to see the rest).
Figure 10–61 Figure 10–62
2
2
4
4
2
6
6
46 108468 2
x
y
2
2
4
4
2
6
6
46 108468 2
x
y
SECTION 10.5 Plane Curves and Parametric Equations 729
tx t
3
1 y 2t
2 7 4
1.5 2.375 3
102
01 0
12 2
1.5 4.375 3
29 4
TECHNOLOGY TIP
To change to parametric graphing
mode, select PAR(AMETRIC) in the fol-
lowing menu/submenu:
TI: MODE
Casio: GRAPH/TYPE
HP-39gs: APLET
In parametric graphing, failure to make appropriate choices for the range of
t-values and the t-step may result in an inaccurate graph, as the next example
illustrates.
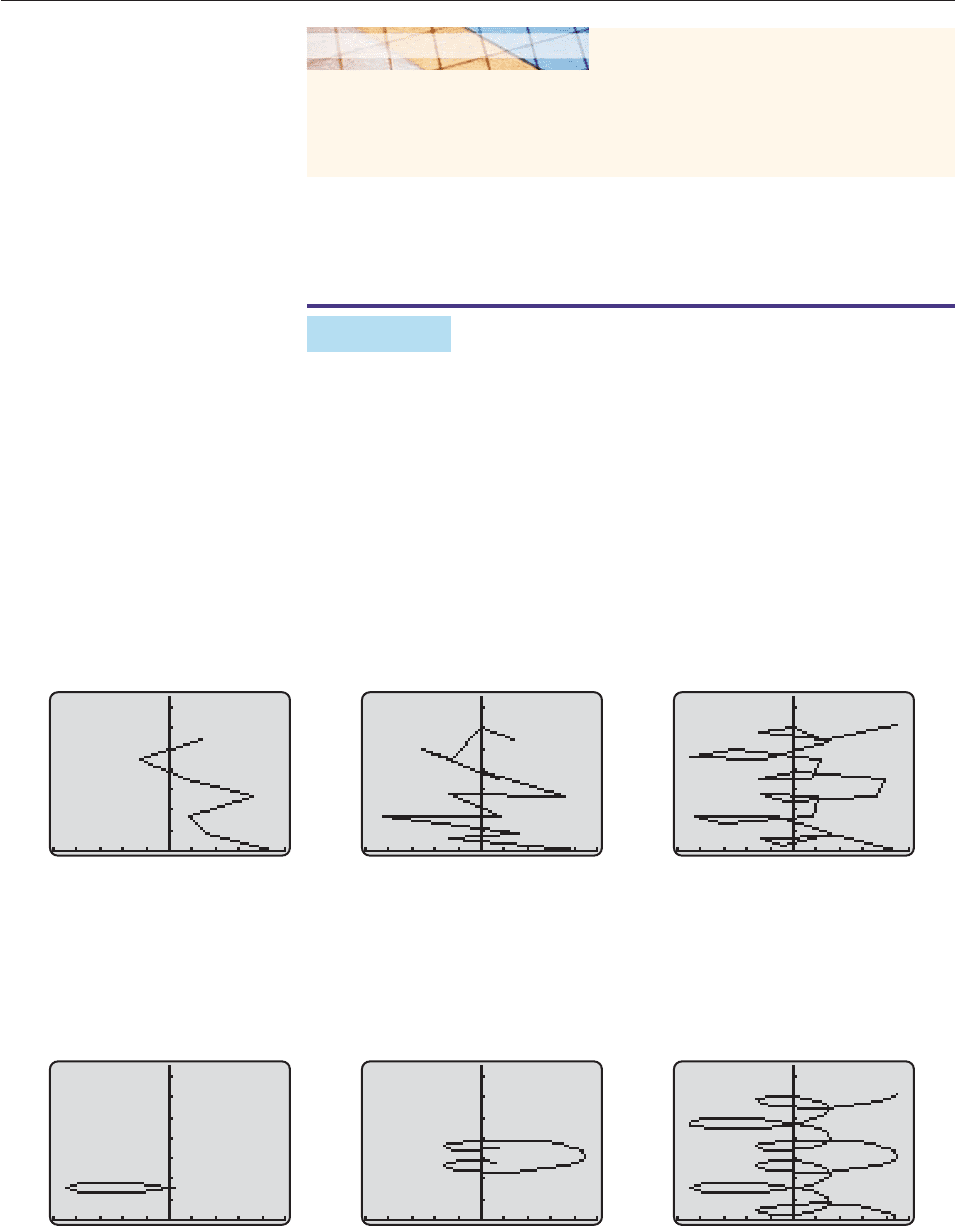
EXAMPLE 2
In the window with 10 x 10 and 0 y 15, graph the curve given by
x 4 cos t 5 cos(3t) and y sin(3t) t
(a) with 0 t 12.5 and each of these t-steps: 2, 1, and .5;
(b) with t-step .1 and each of these ranges: 2.4 t 3.9, 4.6 t 8, and
0 t 12.5.
How do these graphs compare with Figure 10–58?
SOLUTION
(a) The graphs are shown in Figure 10–63. Only the last one looks even remotely
like Figure 10–58.
Figure 10–63
(b) The graphs are shown in Figure 10–64. The first two show only a small portion
of Figure 10–58, but the last one is a complete graph that closely resembles Fig-
ure 10–58, as you verified in the preceding Graphing Exploration. ■
Figure 10–64
0
2.4 ≤ t ≤ 3.9
15
−10 10
0
4.6 ≤ t ≤ 8
15
−10 10
0
0 ≤ t ≤ 12.5
15
−10 10
0
t-step = 2
15
−10 10
0
t-step = 1
15
−10 10
0
t-step = .5
15
−10 10
730 CHAPTER 10 Analytic Geometry
Enter the equations in Figure 10–61 in your calculator and set the viewing window
to match Figure 10–62 (with 0 y 15). Then graph the curve. How does your
graph compare with Figure 10–58? Use the trace feature to see which points corre-
spond to t 0, 1, 2, 3, and 12.5.
GRAPHING EXPLORATION
Example 2 suggests that
A t-step between .05 and 1.5 usually produces a reasonably smooth graph.
Larger t-steps may produce jagged or totally inaccurate graphs. Smaller t-steps
may involve long graphing times and usually don’t improve smoothness very
much.
EXAMPLE 3
Graph the curve given by
x t 5 cos t and y 1 3 sin t
in the viewing window with
24 x 24, 16 y 16, 20 t 20.
SOLUTION See Figure 10–65. Reproduce this graph yourself to see how the
curve spirals along the x-axis. ■
ELIMINATING THE PARAMETER
In some cases a curve given by parametric equations can also be described by a
rectangular equation in x and y. The process of finding such a rectangular equa-
tion is called eliminating the parameter. Here is one method for eliminating the
parameter:
Solve one of the parametric equations for t and substitute this solution
in the other parametric equation. The result is an equation in x and y
whose graph includes the parametric curve.
EXAMPLE 4
Consider the curve given by
x 2t and y 4t
2
4(1 t 2).
(a) Graph the curve.
(b) Eliminate the parameter and find an equation in x and y whose graph includes
the graph in part (a).
SOLUTION
(a) The graph is shown in Figure 10–66.
SECTION 10.5 Plane Curves and Parametric Equations 731
Graph this curve on your calculator, using the same viewing window and range of t
values as in Figure 10–66. In what direction is the curve traced out (that is, what is
the first point graphed (corresponding to t 1) and what is the last point graphed
(corresponding to t 2))?
GRAPHING EXPLORATION
−24 24
−16
16
Figure 10–65
−6
−10 10
14
Figure 10–66
(b) We first solve one of the parametric equations for t. We’ll solve the x-
equation since it is simpler.
x 2t
Divide both sides by 2: t
2
x
Now substitute this result in the y-equation.
y 4t
2
4
Let t
2
x
: y 4
2
x
2
4
y 4
x
4
2
4
y x
2
4.
Therefore, the coordinates of every point on the parametric curve satisfy the
equation y x
2
4. So every point on the curve lies on the graph of
y x
2
4.
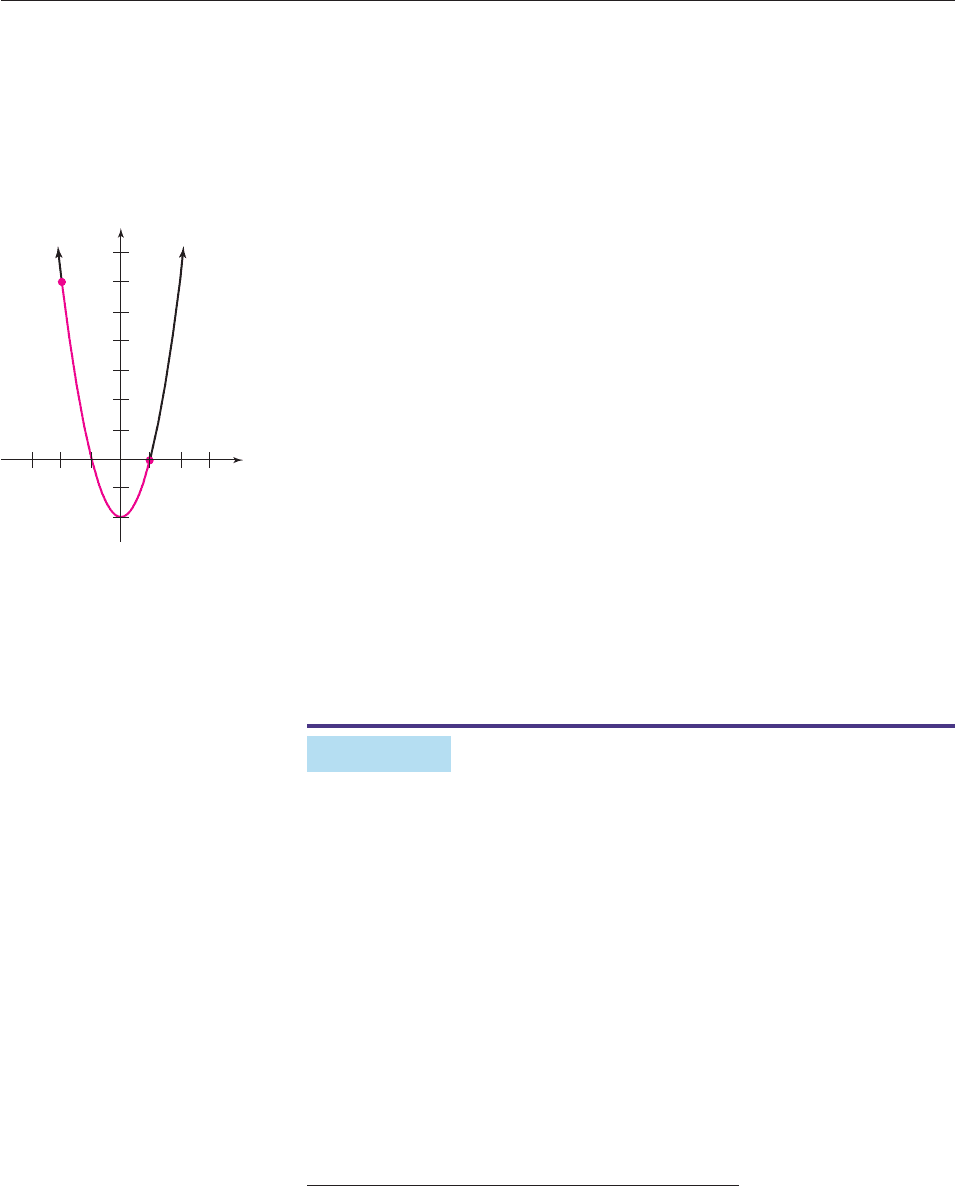
From Section 3.4 and 4.1 we know that the graph of y x
2
4 is the
parabola in Figure 10–67. However, the curve given by the parametric equa-
tions is not the entire parabola, but only the part of it shown in red—the part
from (2, 0) to (4, 12), which corresponds to the minimum and maximum
values of t, namely, t 1 and t 2. ■
When neither parametric equation can be solved for t, other methods are
needed to eliminate the parameter. Appropriate trigonometric identities some-
times do the trick.
EXAMPLE 5
Find a rectangular equation for the witch of Agnesi, which is the curve given by
x cot t and y sin
2
t (0 t p).*
SOLUTION We have
y sin
2
t
y
cs
1
c
2
t
[Reciprocal identity]
y
cot
2
1
t 1
[Pythagorean identity]
y
x
2
1
1
[x cot t]
In this case the parametric curve is the entire rectangular graph because, as t goes
from 0 to p, cot t (which is x here) takes all real values (see Figure 6–85). ■
732 CHAPTER 10 Analytic Geometry
–2
12
2
2
x
y
Figure 10–67
*This curve is a special case of one discussed in a textbook by Maria Agnesi in 1748. Because of its
shape, the curve was called “la versiera” in Italian (meaning “rope that turns into a sail”). When
Agnesi’s book was translated into English, however, the translator mistook “la versiera” for
“l’ aversiera”, which means “the witch”. See Exercises 51–52.
FINDING PARAMETRIC EQUATIONS FOR CURVES
Having seen how to find a rectangular equation that describes a curve given para-
metrically, we now consider the reverse problem: finding a parametric respresen-
tation of an equation in x and y. In two cases, this is easy:
1. If the equation defines y as a function of x, such as
y x
3
5x
2
3x 4,
a parametric description can be found by changing the variable:
x t and y t
3
5t
2
3t 4.
2. If the equation defines x as a function of y, such as
x y
2
3,
a parametric description is given by
x t
2
3 and y t.
EXAMPLE 6
Find a parameterization for the graph of y
3
4y x 5 0 and use it to sketch
the graph.
SOLUTION We rewrite the equation as
x y
3
4y 5,
and see that x is a function of y (each value of y leads to a unique value of x). So
we use the parameterization
x t
3
4t 5 and y t.
The graph is shown in Figure 10–68. ■
EXAMPLE 7
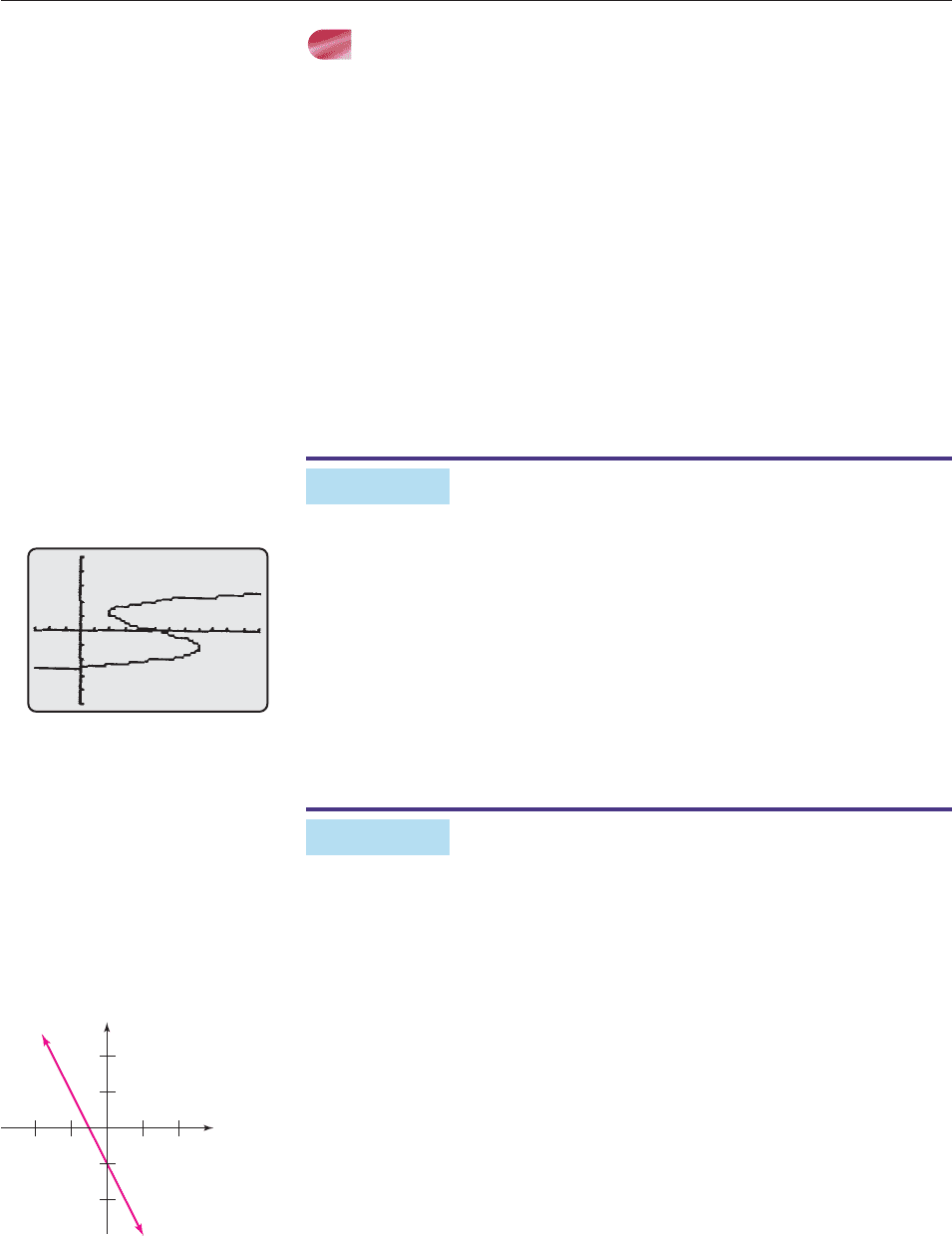
Find three parameterizations of the straight line through (1, 3) with slope 2.
SOLUTION The point-slope form of the equation of this line is
y (3) 2(x 1) or, equivalently, y 2x 1.
Its graph is shown in Figure 10–69. Since this equation defines y as a function of
x, one parameterization is
x t and y 2t 1(t any real number).
A second parameterization is given by letting x t 1; then
y 2x 1 2(t 1) 1 2t 3(t any real number).
A third parameterization can be obtained by letting
x tan t and y 2x 1 2 tan t 1(p/2 t p/2).
When t runs from p/2 to p/2, then x tan t
takes all possible real number val-
ues, and hence so does y. ■
SECTION 10.5 Plane Curves and Parametric Equations 733
5
3
5
12
Figure 10–68
–1
–1
–2
21
x
y
Figure 10–69

Parameterizations of conic sections, such as
(x 3)
2
(y 7)
2
16,
2
x
5
2
y
4
2
1, and
(x
4
3)
2
(y
9
5)
2
1,
are discussed in Special Topics 10.3.A and are summarized in the endpapers at the
beginning of this book. As with lines, there are many ways to parameterize conic
sections.
EXAMPLE 8
In Special Topics 10.3.A we saw that a parameterization of the circle
(x 4)
2
(y 1)
2
9
is given by
(
*
) x 3 cos t 4 and y 3 sin t 1(0 t 2p).
With this parameterization, the circle is traced out in a counterclockwise direction
from the point (7, 1), as shown in Figure 10–70. Another parameterization is given by
x 3 cos 2t 4 and y 3 sin 2t 1(0 t p).
APPLICATIONS
In the following applications, we ignore air resistance and assume some facts
about gravity that are proved in physics.
EXAMPLE 9
Bob Lahr hits a golf ball with an initial velocity of 140 feet per second so that its
path as it leaves the ground makes an angle of 31° with the horizontal.
(a) When does the ball hit the ground?
(b) How far from its starting point does it land?
(c) What is the maximum height of the ball during its flight?
734 CHAPTER 10 Analytic Geometry
CAUTION
Some substitutions in an equation y f (x) do not lead to a parameterization of the entire graph.
For instance, in Example 7, letting x t
2
and substituting in the equation y 2x 1 lead to
x t
2
and y 2t
2
1 (any real number t ).
Thus, x is always nonnegative, and y is always negative. So the parameterization produces only
the half of the line y 2x 1 to the right of the y-axis in Figure 10–69.
Verify that this parameterization traces out the circle in a clockwise direction, twice
as fast as the parameterization given by (
*
), since t runs from 0 to p rather than 2p.
GRAPHING EXPLORATION
■
−3
−210
5
Figure 10–70
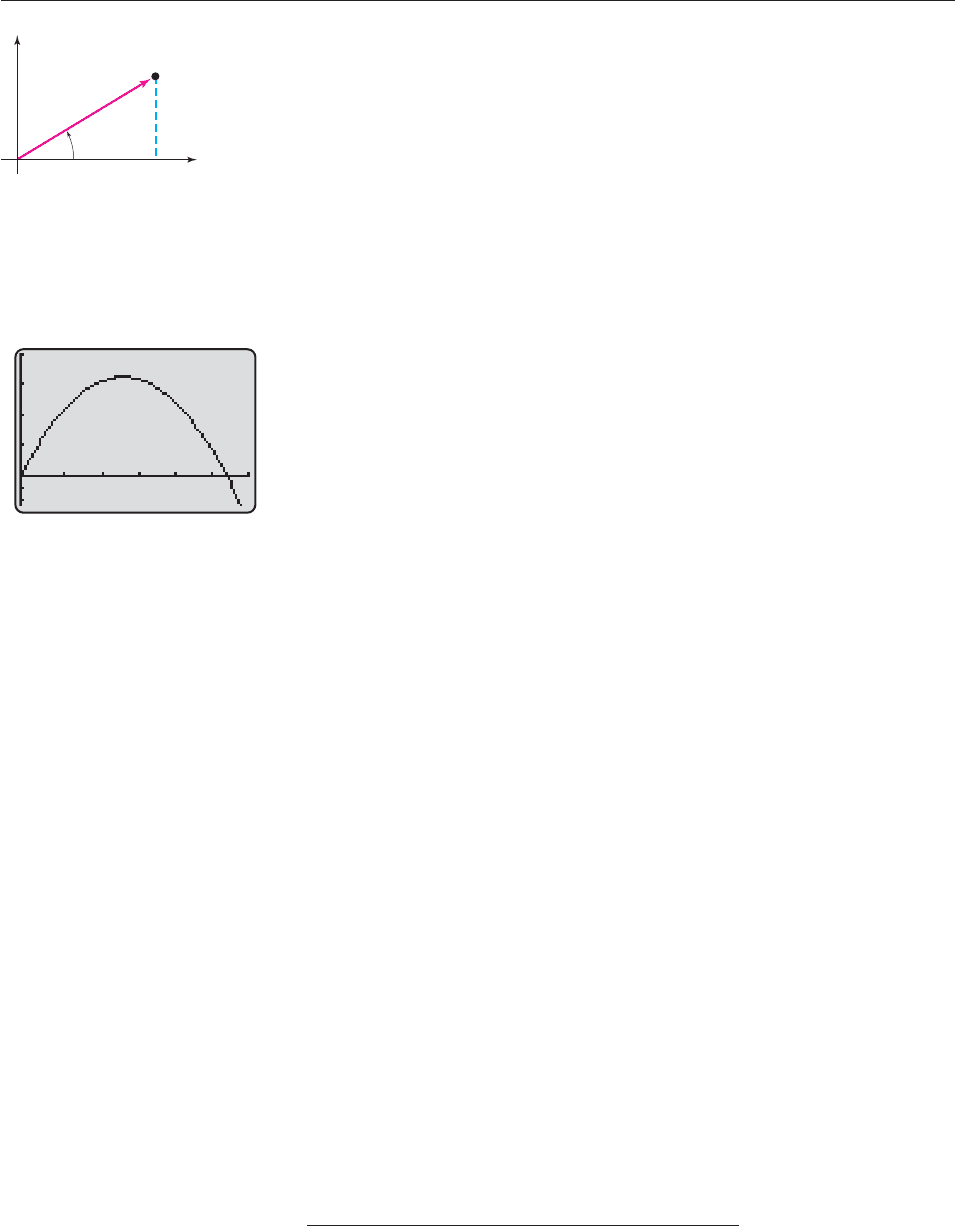
SOLUTION Imagine that the golf ball starts at the origin and travels in the di-
rection of the positive x-axis. If there were no gravity, the distance traveled by the
ball in t seconds would be 140t feet. As shown in Figure 10–71, the coordinates
(x, y) of the ball would satisfy
14
x
0t
cos 31°
14
y
0t
sin 31°,
x (140 cos 31°)ty (140 sin 31°)t.
However, there is gravity, and at time t, it exerts a force of 16t
2
downward (that is,
in the negative direction on the y-coordinate). Consequently, the coordinates of
the golf ball at time t are
x (140 cos 31°)t and y (140 sin 31°)t 16t
2
.
The path given by these parametric equations is graphed in Figure 10–72.*
(a) The ball is on the ground when y 0, that is, at the x-intercepts of the graph.
They can be found geometrically by using trace and zoom-in (the graphical
root finder does not operate in parametric mode), but this is very time-
consuming. To find the intercepts algebraically we need only set y 0 and
solve for t.
(140 sin 31°)t 16t
2
0
t(140 sin 31° 16t) 0
t 0 or 140 sin 31° 16t 0
t
140 s
1
i
6
n 31°
4.5066.
Thus, the ball hits the ground after approximately 4.5066 seconds.
(b) The horizontal distance traveled by the ball is given by the x-coordinate of the
intercept. The x-coordinate when t 4.5066 is
x (140 cos 31°)(4.5066) 540.81 feet.
(c) The graph in Figure 10–72 looks like a parabola, and it is, as you can verify
by eliminating the parameter t (Exercise 56). The y-coordinate of the vertex
is the maximum height of the ball. It can be found geometrically by using
trace and zoom-in (the maximum finder doesn’t work in parametric mode)
or algebraically as follows. The vertex occurs halfway between its two x-
intercepts (x 0 and x 540.81), that is, when x 270.405. Hence,
(140 cos 31°)t x 270.405,
so
t
14
2
0
70
co
.4
s
0
3
5
1°
2.2533.
Therefore, the y-coordinate of the vertex (the maximum height of the ball) is
y (140 sin 31°)(2.2533) 16(2.2533)
2
81.237 feet. ■
SECTION 10.5 Plane Curves and Parametric Equations 735
31°
140 t
x
x
y
y
(x, y)
Figure 10–71
−25
0 600
100
Figure 10–72
*Only the part of the graph on or above the x-axis represents the ball’s path, since the ball does not go
underground after it lands.
