Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

SOLUTION This equation has the form of the second equation in the preced-
ing box, with h 0, k 0, a 3, and b 4. So the parametric equations are
x 4 tan t and y
co
3
s t
(0 t 2p). ■
EXAMPLE 5
Find parametric equations for the hyperbola whose equation is
(x
4
3)
2
(y
9
5)
2
1.
SOLUTION We begin by rewriting the equation as
(x
2
2
3)
2
(y
3
(
2
5))
2
1.
Now the equation has the form of the first equation in the box above, with h 3,
k 5, a 2, and b 3. So the parametric equations are
x
co
2
s t
3 and y 3 tan t 5(0 t 2p).
PARABOLAS
If a parabola has an equation in which there is an x
2
term, but no y
2
term, such as
y 4x
2
3x 1orx
2
2y or (x h)
2
4p(y k),
then it can be easily graphed: Solve the equation for y and graph in the ordinary
way. Parametric equations aren’t needed because, in each of these cases, y is a
function of x.*
When a parabola has an equation in which there is a y
2
term, but no x
2
term
such as
x y
2
8y 13 or 2y
2
8x,
then solving for y leads to two equations to be graphed on the same screen. In such
cases parametric equations provide an easier way to graph the parabola, as illus-
trated in the next example.
716 CHAPTER 10 Analytic Geometry
*However, if you insist graphing y 4x
2
3x 1 parametrically, you can do so by letting x t and
y 4t
2
3t 1 (which amounts to changing the name of the variable x to t)—and similarly in the
other cases shown above.
Graph this hyperbola in the window with 9 x 9 and 6 y 6. Note that
tan t is not defined when t p/2. The calculator graphs values of t that are slightly
smaller and slightly larger than p/2 and connects them, which produces an erro-
neous straight line in the figure. The same thing happens at t 3p/2.
GRAPHING EXPLORATION
Use these parametric equations to graph the hyperbola in the viewing window with
6 x 12 and 11 y 1.
■
GRAPHING EXPLORATION

EXAMPLE 6
Use parametric equations to graph y
2
13 8y x.
SOLUTION We first solve the equation for x:
x y
2
8y 13.
This is the equation of a parabola. Furthermore, the equation shows that x is a
function of y (each value of y produces a unique value of x). Consequently, we can
graph this equation by using the parametric equations
x t
2
8t 13
y t (t any real number),
as explained in Special Topics 3.3.A on page 178. The graph is shown in
Figure 10–50. ■
The parametric graphing technique used in Example 6 can be applied to the
parabola with equation (y k)
2
4p(x h) by solving the equation for x and
letting y t.
SPECIAL TOPICS 10.3.A Parametric Equations for Conic Sections 717
Parametric Equations
for Parabolas
The parabola with vertex (h, k) and equation
(y k)
2
4p(x h)
is given by the parametric equations
x
(t
4p
k)
2
h and y t (t any real number).
EXERCISES 10.3.A
In Exercises 1–28, find parametric equations for the conic
section whose rectangular equation is given, and use them to
find a complete graph of the conic.
1. x
2
y
2
25 2. x
2
y
2
40
3. (x 4)
2
(y 2)
2
9 4. (x 1)
2
1 (y 1)
2
5. (x 1)
2
5 y
2
6. x
2
4x 4 9 y
2
6y 9
7.
1
x
0
2
1
3
y
6
2
8.
4
y
9
2
8
x
1
2
1
9. 4x
2
4y
2
1 10. x
2
4y
2
1
11.
(x
4
1)
2
(y
9
5)
2
1
12.
(x
16
2)
2
(y
12
3)
2
1
13.
(x
16
1)
2
(y
8
4)
2
1
14.
(x
4
5)
2
(y
12
2)
2
1
15.
1
x
0
2
3
y
6
2
1 16.
y
9
2
1
x
6
2
1
17. x
2
4y
2
1 18. 2x
2
y
2
4
15
5
5
25
Figure 10–50
NOTE
The rectangular and parametric equations for conic sections are summarized in the endpapers at
the beginning of the book.

718 CHAPTER 10 Analytic Geometry
19.
(y
25
3)
2
(x
16
1)
2
1 20.
(y
9
1)
2
(x
25
1)
2
1
21.
(x
1
3)
2
(y
4
2)
2
1 22.
(y
9
5)
2
(x
1
2)
2
1
23. 8x 2y
2
24. 4y x
2
25. y 4(x 1)
2
2 26. y 3(x 2)
2
3
27. x 2(y 2)
2
28. x 3(y 1)
2
2
In Exercises 29–38, identify the conic section whose paramet-
ric equations are given without graphing. For circles, list the
center and radius. For ellipses and hyperbolas, list the center.
For parabolas, list the vertex.
29. x 3 cos t and y 3 sin t 5(0 t 2p)
30. x 7 cos t 4 and y 7 sin t 3(0 t 2p)
31. x 3 cos t 4 and y 5 sin t (0 t 2p)
32. x 6 cos t 4 and y 3 sin t 4(0 t 2p)
33. x
co
2
s t
2 and y 4 tan t 4(0 t 2p)
34. x tan t 3 and y
co
7
s t
5(0 t 2)
35. x 4 tan t and y
co
3
s t
3(0 t 2p)
36. x
co
1
s t
1 and y 3 tan t 2(0 t 2p)
37. x
(t
4
4)
2
3 and y t (t any real number)
38. x
(t
2
2)
2
2 and y t (t any real number)
THINKERS
39. (a) Verify that the curve with parametric equations
x cos (.5t) and y sin (.5t)(0 t 2p)
lies on the circle x
2
y
2
1. [Hint: Use the argument
in Example 1.]
(b) Verify that the curve with parametric equations
x cos (.5t) and y sin (.5t)(0 t 2p)
lies on the circle x
2
y
2
1.
(c) Explain why neither of the curves in parts (a) and (b) is
a complete circle. [Hint: What are the periods of
cos(.5t) and sin(.5t)?]
In Exercises 40–41, use parametric equations (and trial and
error) to draw a face on your calculator screen that closely
resembles the one shown. [Hint: Use a square viewing window.
Let the head be a circle with center at the origin and radius 3.
Let the eyes be smaller circles with appropriate centers and
radii. Let the mouth be a half circle (see Exercise 39). Finally,
turn off the axes on your calculator screen.*
]
40. 41.
In Exercises 42–43, use parametric equations (and trial and
error) to draw a face on your calculator screen that closely
resembles the one shown. [Hint: Adapt the hint for Exercises
40–41, using ellipses in place of circles.]
42. 43.
*In the FORMAT menu of TI-84+; in the GRAPH SET-UP menu of
Casio 9850; on the second page of the PLOT SET-UP menu of HP-39gs.
10.4 Rotations and Second-Degree Equations
■ Use the discriminant to identify the graph of a second-degree
equation.
A second-degree equation in x and y is one that can be written in the form
Ax
2
Bxy Cy
2
Dx Ey F 0
for some constants A, B, C, D, E, F, with at least one of A, B, C nonzero.
Section Objective

EXAMPLE 1
Show that each of the following conic sections is the graph of a second-degree
equation.
(a) Ellipse:
x
6
2
y
5
2
1 (b) Hyperbola:
(x
4
1)
2
(y
6
3)
2
1
SOLUTION We need only show that each of these equations is in fact a second-
degree equation. In each case, eliminate denominators, multiply out all terms, and
gather them on one side of the equal sign.
(a)
x
6
2
y
5
2
1
Multiply both sides by 30: 5x
2
6y
2
30
Rearrange terms: 5x
2
6y
2
30 0.
This equation is a second-degree equation because it has the form
Ax
2
Bxy Cy
2
Dx Ey F 0
with A 5, B 0, C 6, D 0, E 0, and F 30.
(b)
(x
4
1)
2
(y
6
3)
2
1
Multiply both sides by 12: 3(x 1)
2
2(y 3)
2
12
Multiply out left side: 3(x
2
2x 1) 2(y
2
6y 9) 12
3x
2
6x 3 2y
2
12y 18 12
Rearrange terms: 3x
2
2y
2
6x 12y 27 0.
This is a second-degree equation with A 3, B 0, C 2, D 6,
E 12, and F 27. ■
Calculations like those in Example 1 can be used on the equation of any conic
section to show that it is the graph of a second-degree equation. Conversely, it can
be shown that
The graph of every second-degree equation is a conic section
(possibly degenerate). When the second-degree equation has no xy-term (that is,
B 0), as was the case in Example 1, the graph is a conic section in standard
position (axis or axes parallel to the coordinate axes). When B 0, however, the
conic is rotated from standard position, so its axis or axes are not parallel to the
coordinate axes.
EXAMPLE 2
Graph the equation
3x
2
6xy y
2
x 2y 7 0.
SECTION 10.4 Rotations and Second-Degree Equations 719
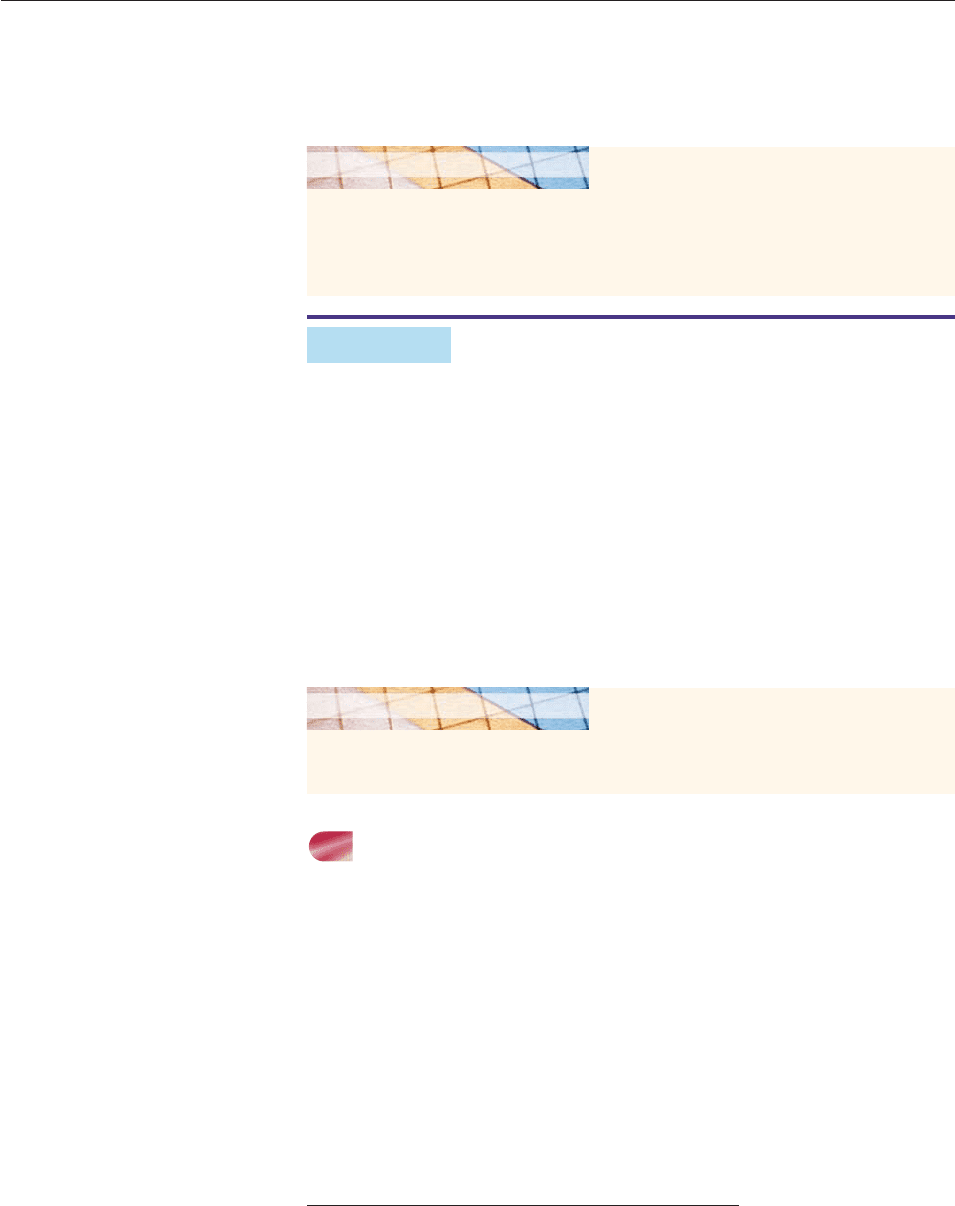
SOLUTION We first rewrite it as
y
2
6xy 2y 3x
2
x 7 0
y
2
(6x 2)y (3x
2
x 7) 0.
This equation has the form ay
2
by c 0, with a 1, b 6x 2, and
c 3x
2
x 7. It can be solved by using the quadratic formula
y
b
2a
b
2
4
ac
.
The top half of the graph is obtained by graphing
y ,
and the bottom half is obtained by graphing
y .
The graph is a hyperbola whose focal axis tilts upward to the left, as shown in
Figure 10–51. ■
THE DISCRIMINANT
The following fact, whose proof is outlined in Exercise 15 of Special Topics
10.4.A, makes it easy to identify the graphs of second-degree equations without
graphing them.
The expression B
2
4AC is called the discriminant of the equation.
EXAMPLE 3
Identify the graph of
2x
2
4xy 3y
2
5x 6y 8 0
and sketch the graph.
SOLUTION We compute the discriminant with A 2, B 4, and C 3.
B
2
4AC (4)
2
4
2
3 16 24 8.
6x 2
(6x
2)
2
4(3x
2
x 7
)
2
6x 2
(6x
2)
2
4(3x
2
x
7)
2
(6x 2)
(6x
2)
2
4
1
(3x
2
x 7
)
2
1
720 CHAPTER 10 Analytic Geometry
−10
−88
8
Figure 10–51
Graphs of
Second-Degree
Equations
If the equation
Ax
2
Bxy Cy
2
Dx Ey F 0(A, B, C not all 0)
has a graph, then that graph is
A circle or an ellipse (or a point), if B
2
4AC 0;
A parabola (or a line or two parallel lines), if B
2
4AC 0;
A hyperbola (or two intersecting lines), if B
2
4AC 0.
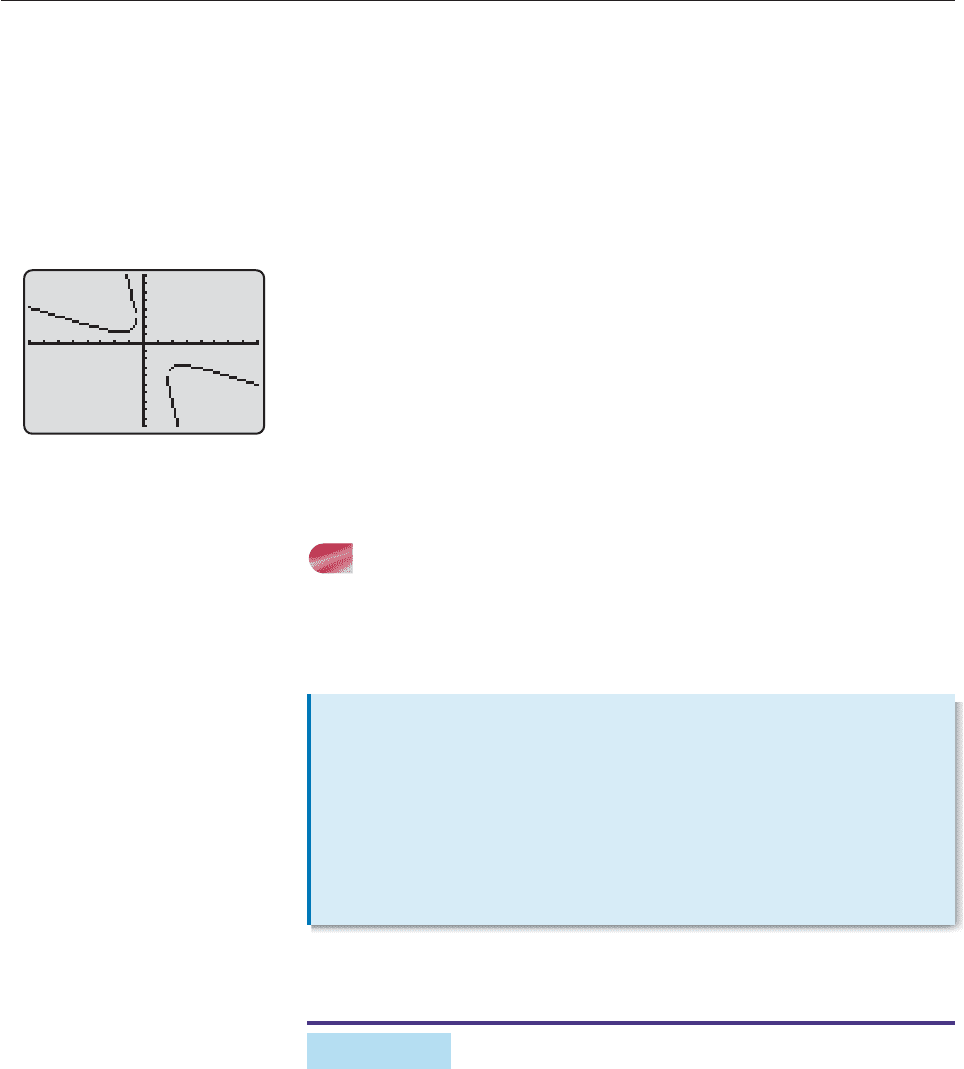
Hence, the graph is an ellipse (possibly a circle or a single point). To find the
graph, we rewrite the equation as
3y
2
4xy 6y 2x
2
5x 8 0
3y
2
(4x 6)y (2x
2
5x 8) 0.
The equation has the form ay
2
by c 0 and can be solved by the quadratic
formula.
y
b
2a
b
2
4
ac
.
The graph can now be found by graphing the last two equations on the same screen.
EXAMPLE 4
Does Figure 10–52 show a complete graph of
3x
2
5xy 2y
2
8y 1 0?
SOLUTION Although the graph in the figure looks like a parabola, appear-
ances are deceiving. The discriminant of the equation is
B
2
4AC 5
2
4
3
2 1,
which means that the graph is a hyperbola. So Figure 10–52 cannot possibly be a
complete graph of the equation.*
■
(4x 6)
(4x
6)
2
4
3
(2x
2
5x
8)
2
3
SECTION 10.4 Rotations and Second-Degree Equations 721
*When one of the authors asked students to graph this equation on an examination, many of them did
not bother to compute the discriminant and produced something similar to Figure 10–52. They didn’t
get much credit for this answer. Moral: Use the discriminant to identify the conic so that you know the
shape of the graph you are looking for.
Find a viewing window that shows a complete graph of the equation. In what direc-
tion does the major axis run?
GRAPHING EXPLORATION
■
−4
4
−4.7 4.7
Figure 10–52
Solve the equation for y, as in Example 3. Then find a viewing window that clearly
shows both branches of the hyperbola.
GRAPHING EXPLORATION
EXAMPLE 5
Sketch the graph of
3x
2
6xy 3y
2
13x 9y 53 0.
SOLUTION The discriminant is B
2
4AC 6
2
4
3
3 0. Hence, the
graph is a parabola (or a line or parallel lines in the degenerate case). ■
GRAPHING EXPLORATION
Find a viewing window that
shows a complete graph of the
equation.
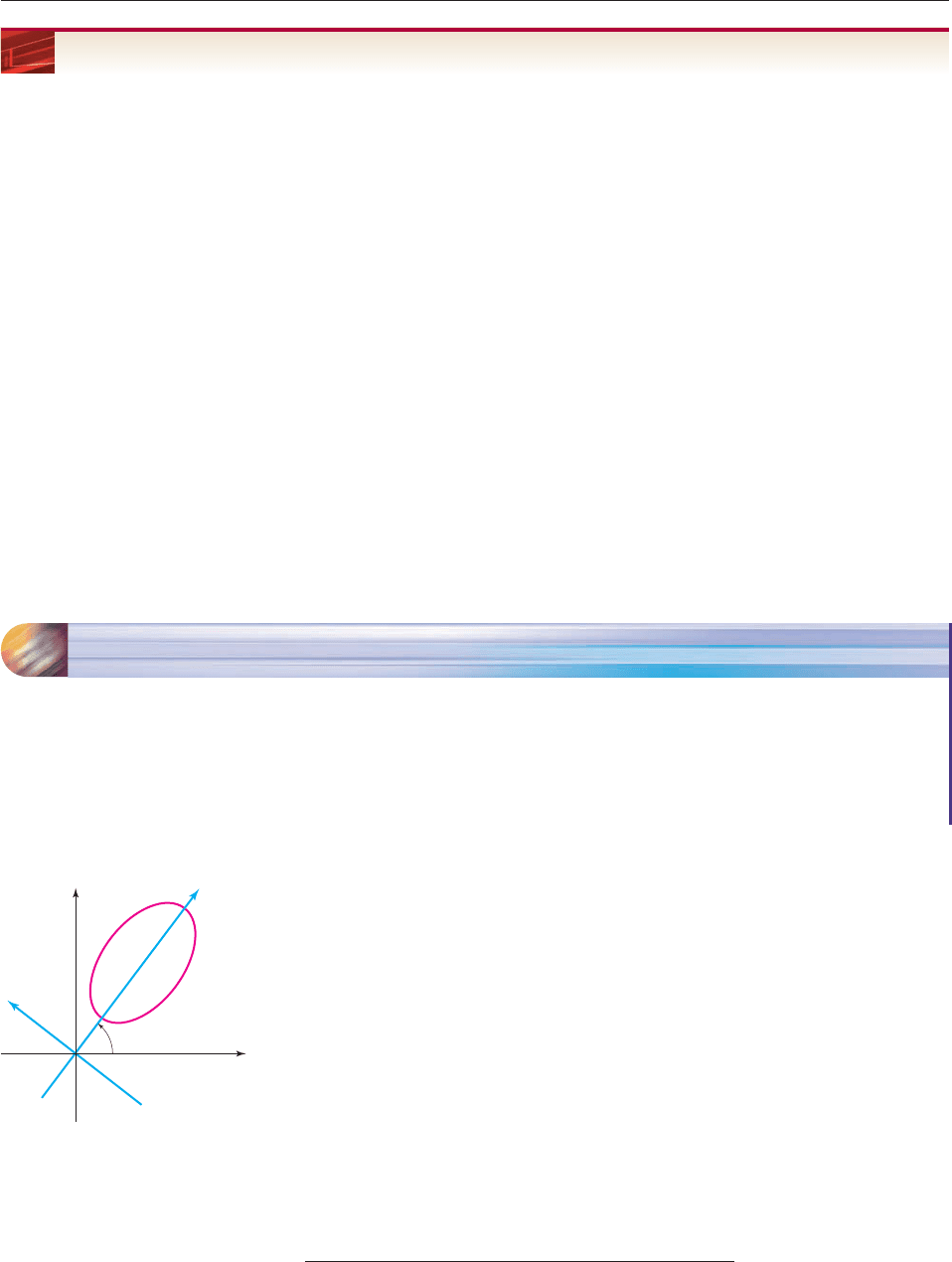
722 CHAPTER 10 Analytic Geometry
EXERCISES 10.4
In Exercises 1–6, assume that the graph of the equation is a
nondegenerate conic section. Without graphing, determine
whether the graph an ellipse, hyperbola, or parabola.
1. x
2
2xy 3y
2
1 0
2. xy 1 0
3. x
2
2xy y
2
22
x 22
y 0
4. 2x
2
4xy 5y
2
6 0
5. 17x
2
48xy 31y
2
50 0
6. 2x
2
4xy 2y
2
3x 5y 10 0
In Exercises 7–24, use the discriminant to identify the conic
section whose equation is given, and find a viewing window
that shows a complete graph.
7. 9x
2
4y
2
54x 8y 49 0
8. 4x
2
5y
2
8x 30y 29 0
9. 4y
2
x
2
6x 24y 11 0
10. x
2
16y
2
0
11. 3y
2
x 2y 1 0
12. x
2
6x y 5 0
13. 41x
2
24xy 34y
2
25 0
14. x
2
23
xy 3y
2
83
x 8y 32 0
15. 17x
2
48xy 31y
2
49 0
16. 52x
2
72xy 73y
2
200
17. 9x
2
24xy 16y
2
90x 130y 0
18. x
2
10xy y
2
1 0
19. 23x
2
263
xy 3y
2
16x 163
y 128 0
20. x
2
2xy y
2
122
x 122
y 0
21. 17x
2
12xy 8y
2
80 0
22. 11x
2
24xy 4y
2
30x 40y 45 0
23. 3x
2
23
xy y
2
4x 43
y 16 0
24. 3x
2
22
xy 2y
2
12 0
■ Use the rotation equations to express a second-degree equation
in x and y as an equation in u and v.
■ Determine the angle of rotation needed to write a second-degree
equation in x and y as an equation in u and v that has no uv
term.
We have seen that the graph of the second-degree equation
Ax
2
Bxy Cy
2
Dx Ey F 0(B 0)
is a conic section whose axes are not parallel to the coordinate axes, as in Fig-
ure 10–53. Although we can graph the equation on a calculator (as in Section 10.4),
we cannot read off useful information about the center, vertices, etc. from the
equation, as we can from an equation in standard form.
The key is to replace the xy coordinate system by a new coordinate system, as
indicated by the blue u- and v-axes in Figure 10–53. The conic is not rotated in the
new coordinate system, so it has an equation (in u and v) in standard form that will
provide the desired information.
To use this approach, we must first determine the relationship between the xy
coordinates of a point and its coordinates in the uv system. Suppose the uv coordinate
system is obtained by rotating the xy axes about the origin, counterclockwise
through an angle u.* If a point P has coordinates (x, y) in the xy system, we can find
its coordinates (u, v) in the rotated coordinate system by using Figure 10–54.
10.4.A SPECIAL TOPICS Rotation of Axes
y
v
u
x
q
Figure 10–53
*All rotations in this section are counterclockwise about the origin, with 0° u 90°.
Section Objectives
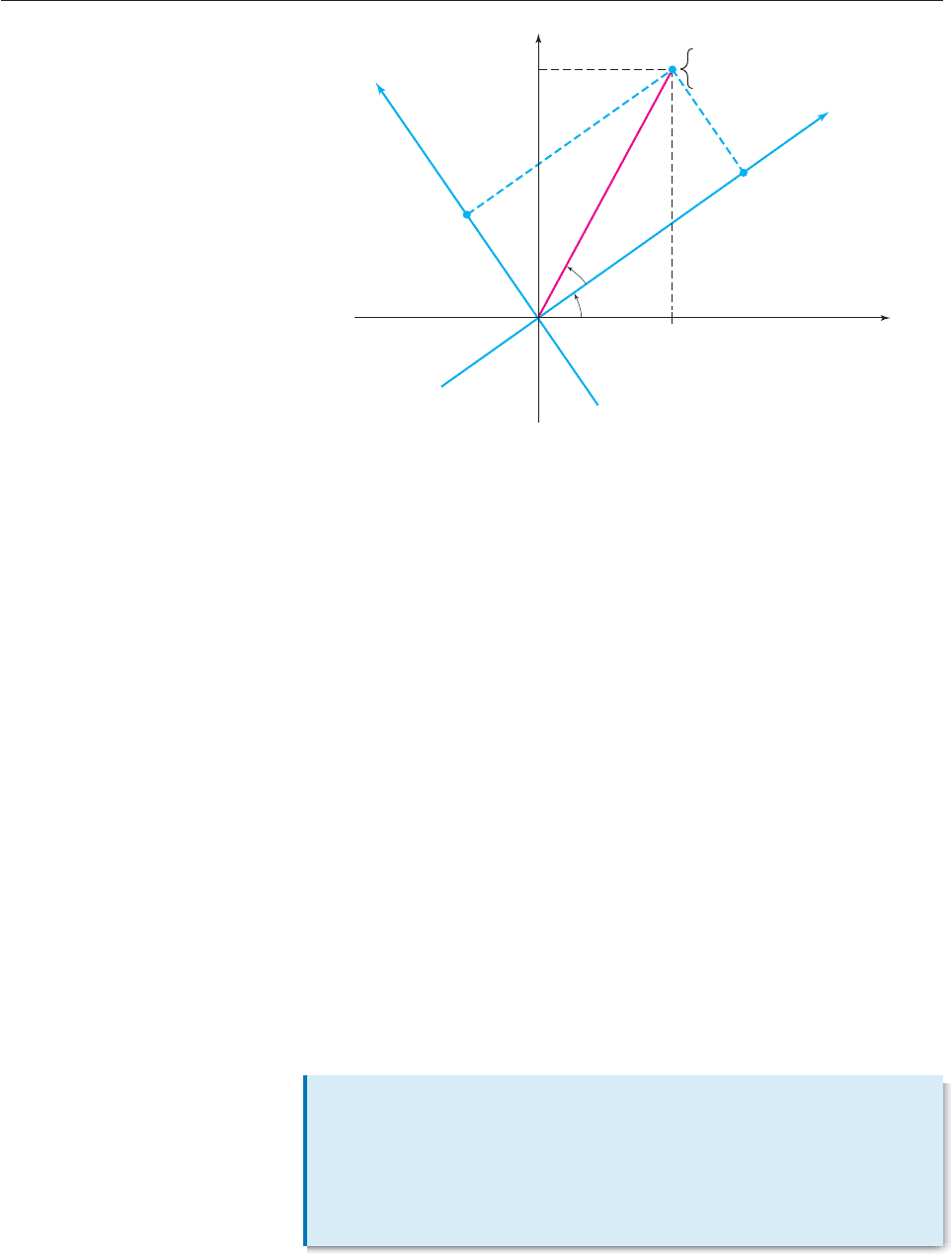
Figure 10–54
Triangle OPQ shows that
cos b
O
O
Q
P
u
r
and sin b
P
O
Q
P
v
r
.
Therefore,
u r cos b and v r sin b.
Similarly, triangle OPR shows that
cos(u b)
O
O
R
P
x
r
and sin(u b)
O
PR
P
y
r
,
so
x r cos(u b) and y r sin(u b).
Applying the addition identity for cosine (page 524) shows that
x r cos(u b)
r(cos u cos b sin u sin b)
(r cos b) cos u (r sin b) sin u
u cos u v sin u.
A similar argument with y r sin(u b) and the addition identity for sine leads
to this result.
y
x
(x, y)
(u, v)
u
u
r
v
R
x
y
v
O
Q
P
θ
β
SPECIAL TOPICS 10.4.A Rotation of Axes 723
The Rotation
Equations
If the xy coordinate axes are rotated through an angle u to produce the uv
coordinate axes, then the coordinates (x, y) and (u, v) of a point are related
by these equations:
x u cos u v sin u,
y u sin u v cos u.
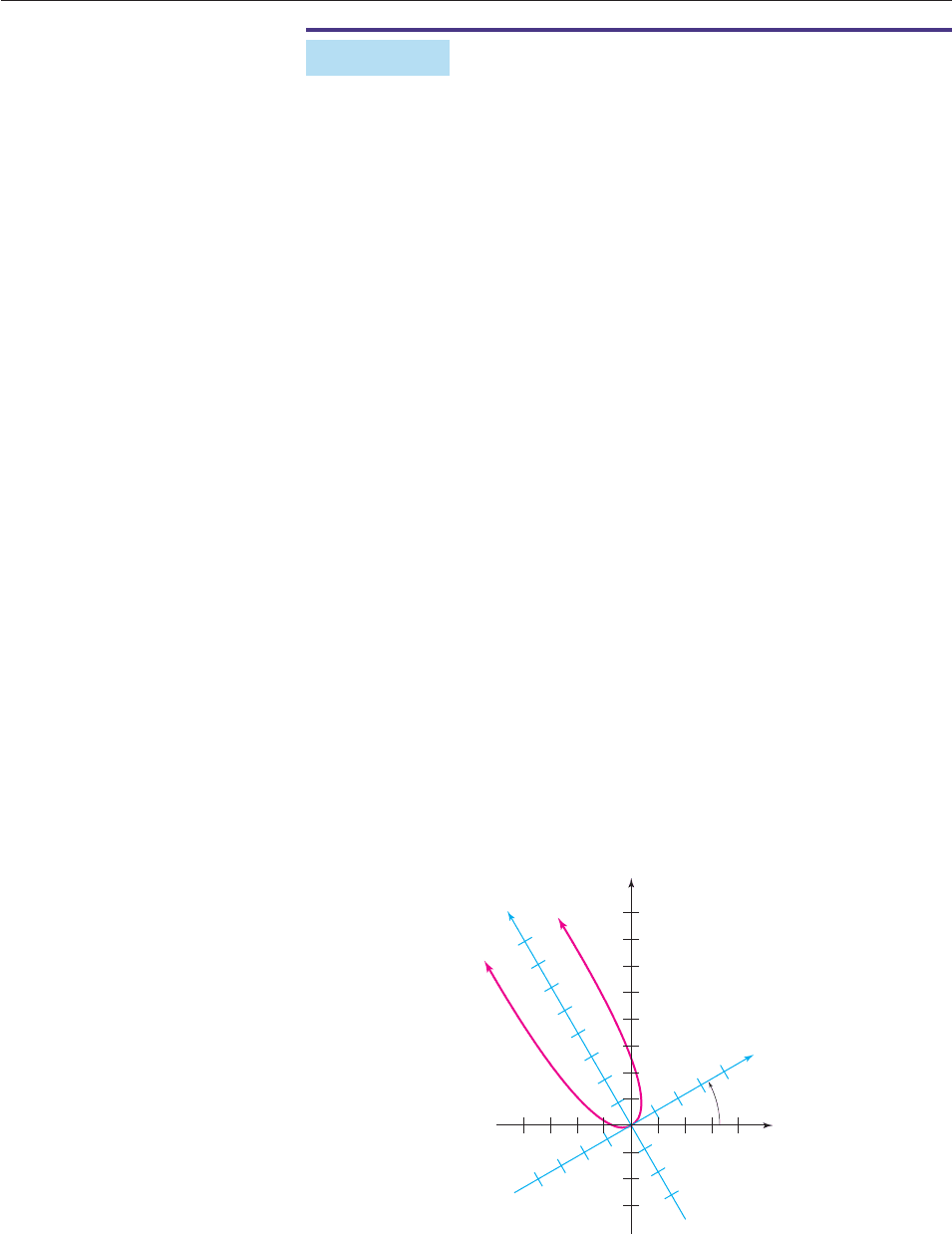
EXAMPLE 1
If the xy axes are rotated 30°, find the equation relative to the uv axes of the
graph of
3x
2
23
xy y
2
x 3
y 0,
and graph the equation.
SOLUTION Since sin 30° 1/2 and cos 30° 3
/2, the rotation equations
are
x u cos 30° v sin 30°
2
3
u
1
2
v,
y u sin 30° v cos 30°
1
2
u
2
3
v.
Substitute these expressions in the original equation.
3x
2
23
xy y
2
x 3
y 0
3
2
3
u
1
2
v
2
23
2
3
u
1
2
v
1
2
u
2
3
v
1
2
u
2
3
v
2
2
3
u
1
2
v
3
1
2
u
2
3
v
0
3
3
4
u
2
2
3
uv
1
4
v
2
23
4
3
u
2
1
2
uv
4
3
v
2
1
4
u
2
2
3
uv
3
4
v
2
2
3
u
1
2
v
3
1
2
u
2
3
v
0.
Verify that the last equation simplifies as
4u
2
2v 0 or, equivalently, v 2u
2
.
In the uv system, v 2u
2
is the equation of an upward-opening parabola with ver-
tex at (0, 0) as shown in Figure 10–55. ■
Figure 10–55
30°
1
y
x
1
u
v
724 CHAPTER 10 Analytic Geometry
Rotating the axes in the preceding example changed the original equation,
which included an xy term, to an equation that had no uv term. That enabled us
to identify the graph of the new equation as a conic section. This can be done for
any second-degree equation by choosing an angle of rotation that will eliminate
the xy term. The choice of the angle is determined by this fact, which is proved in
Exercise 13.
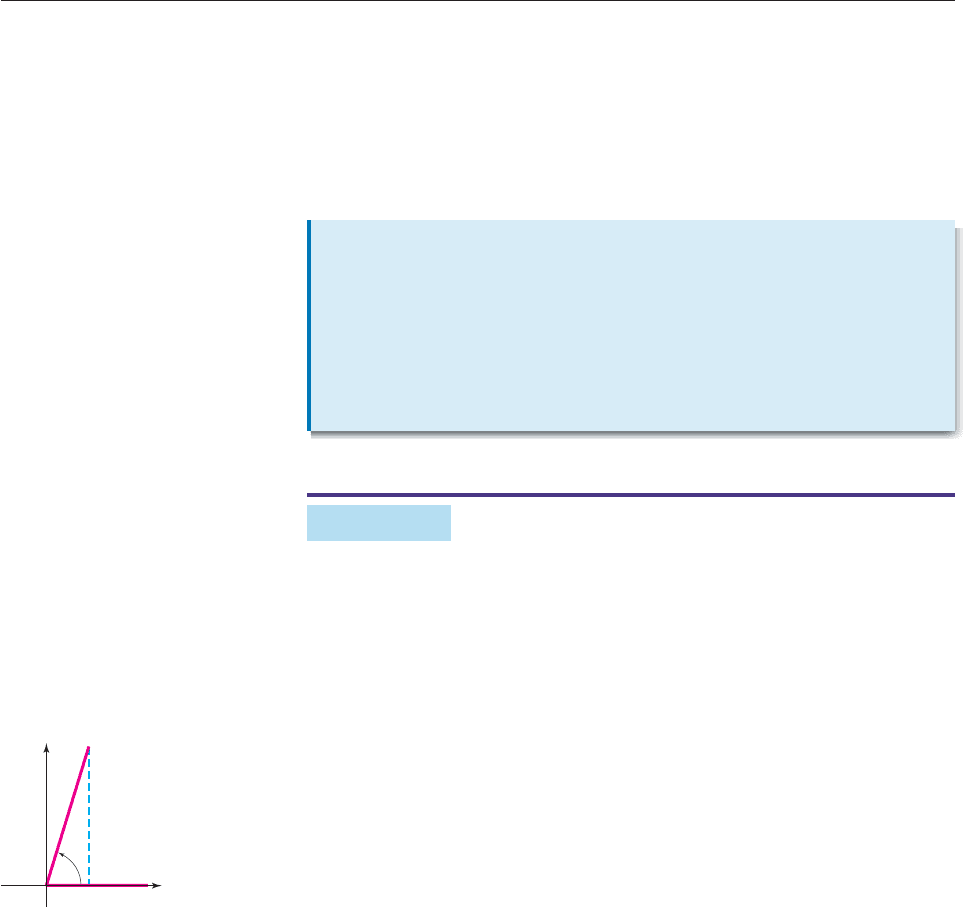
EXAMPLE 2
What angle of rotation will eliminate the xy term in the equation
153x
2
192xy 97y
2
1710x 1470y 5625 0,
and what are the rotation equations in this case?
SOLUTION According to the fact in the box with A 153, B 192, and
C 97, we should rotate through an angle of u, where
cot 2u
153
19
2
97
1
5
9
6
2
2
7
4
.
Since 0° 2u 180° and cot 2u is positive, the terminal side of the angle 2u lies
in the first quadrant, as shown in Figure 10–56. The hypotenuse of this triangle
has length
7
2
2
4
2
625
25. Hence, cos 2u 7/25. The half-angle
identities with x 2u (page 538) show that
sin u
1 c
2
o
s2u
1
2
7/
25
2
9
5
3
5
,
cos u
1 c
2
o
s2u
1
2
7/
25
1
2
6
5
4
5
.
Using sin u 3/5 and the SIN
1
key on a calculator, we find that the angle u of
rotation is approximately 36.87°. The rotation equations are
x u cos u v sin u
4
5
u
3
5
v,
y u sin u v cos u
3
5
u
4
5
v. ■
SPECIAL TOPICS 10.4.A Rotation of Axes 725
Rotation
Angle
The equation Ax
2
Bxy Cy
2
Dx Ey F 0 (B 0) can be rewrit-
ten as Au
2
Cv
2
Du Ev F0 by rotating the xy axes through
an angle u such that
cot 2u
A
B
C
(0° u 90°)
and using the rotation equations.
2
θ
24
7
Figure 10–56
