Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

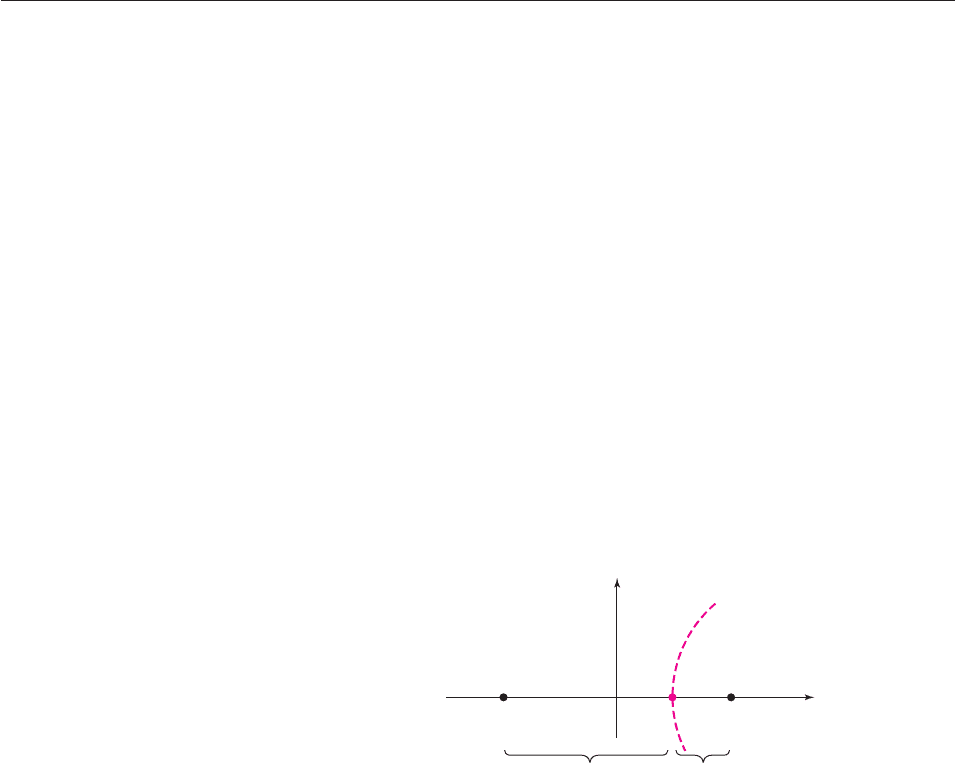
Since 1 mile is 5280 feet, this means that
d
1
d
2
517,440/5,280 miles 98 miles.
In other words,
(Distance from P to S) (Distance from Q to S ) d
1
d
2
98.
This is precisely the situation described in the definition of “hyperbola” on
pages 686–687: S is on the hyperbola with foci P (100, 0), Q (100, 0), and
distance difference r 98. This hyperbola has an equation of the form
x
a
2
2
y
b
2
2
1,
where (a, 0) are the vertices, (c, 0) (100, 0) are the foci, and c
2
a
2
b
2
.
Figure 10–29 and the fact that the vertex (a, 0) is on the hyperbola show that
[Distance from P to (a, 0)] [Distance from Q to (a, 0)] r 98
(100 a) (100 a) 98
2a 98
a 49.
Figure 10–29
Consequently, a
2
49
2
2401, and hence, b
2
c
2
a
2
100
2
49
2
7599.
Thus, the ship lies on the hyperbola
(
*
)
24
x
0
2
1
75
y
9
2
9
1.
A similar argument using P and R as foci shows that the ship also lies on the
hyperbola with foci P (100, 0) and R (300, 0) and center (200, 0), whose dis-
tance difference r is
d
1
d
3
980
305 298,900 feet 56.61 miles.
As before, you can verify that a 56.61/2 28.305, and hence, a
2
28.305
2
801.17. This hyperbola has center (200, 0), and its foci are (200 c, k) (100, 0)
and (200 c, k) (300, 0), which implies that c 100. Hence, b
2
c
2
a
2
100
2
801.17 9198.83, and the ship also lies on the hyperbola
(
**
)
(x
8
01
2
.1
0
7
0)
2
919
y
8
2
.83
1.
y
P
Q
a
−100 100
100 − a100 + a
(a, 0)
x
696 CHAPTER 10 Analytic Geometry
Since the ship lies on both hyperbolas, its coordinates are solutions of both the equa-
tions (
*
) and (
**
). They can be found algebraically by solving each of the equations
for y
2
, setting the results equal, and solving for x. They can be found geometrically
by graphing both hyperbolas and finding the intersection point. As shown in Fig-
ure 10–30, there are actually four points of intersection. However, the two below the
x-axis represent points on land in our situation. Furthermore, since the signal from
P was received first, the ship is closest to P. So it is located at the point S in Fig-
ure 10–30. A graphical intersection finder shows that this point is approximately
(130.48, 215.14), where the coordinates are in miles from the origin. ■
SECTION 10.2 Hyperbolas 697
S
Q
P
R
−900
−500 500
900
Figure 10–30
EXERCISES 10.2
In Exercises 1–6, determine which of the following equations
could possibly have the given graph.
3x
2
3y
2
12, 6y
2
x
2
6,
x
2
4y
2
1, 4x
2
4(y 2)
2
12,
4(x 4)
2
4y
2
12, 6x
2
2y
2
18
2x
2
y
2
8, 3x
2
y 6
1.
2.
3.
y
x
x
y
y
x
4.
5.
6.
In Exercises 7–14, identify the conic section whose equation
is given and find its graph. List its vertices, foci, and
asymptotes.
7.
x
4
2
y
2
1 8.
x
6
2
1
y
6
2
1
9. 3y
2
5x
2
15 10. 4x
2
y
2
16
11.
y
9
2
1
x
6
2
1 12.
1
x
0
2
3
y
6
2
1
13. x
2
4y
2
1 14. 2x
2
y
2
4
y
x
y
x
y
x
698 CHAPTER 10 Analytic Geometry
In Exercises 15–20, find the equation of the hyperbola.
15.
16.
17.
18.
2
2
4
4
2
6
8
6
8
468468 2
x
y
2
2
4
4
2
6
8
6
8
468468 2
x
y
2
2
4
4
2
6
8
6
8
468468 2
x
y
2
2
4
4
2
6
8
6
8
468468 2
x
y
19.
20.
In Exercises 21–24, find the equation of the hyperbola that
satisfies the given conditions.
21. Center (0, 0); x-intercepts 3; asymptote y 2x.
22. Center (0, 0); y-intercepts 12; asymptote y 3x/2.
23. Center (0, 0); vertex (2, 0); passing through (4, 3
).
24. Center (0, 0); vertex (0, 12); passing through (2 3
, 6).
In Exercises 25–32, identify the conic whose equation is given
and find its graph. If it is an ellipse, list its center, vertices,
and foci. If it is a hyperbola, list its center, vertices, foci, and
asymptotes.
25.
(y
25
3)
2
(x
16
1)
2
1
26.
(y
9
1)
2
(x
25
1)
2
1
27.
(x
1
3)
2
(y
4
2)
2
1
28.
(y
9
5)
2
(x
1
2)
2
1
29. (y 4)
2
8(x 1)
2
8
30. (x 3)
2
12(y 2)
2
24
31. 4y
2
x
2
6x 24y 11 0
32. x
2
16y
2
0
2
2
4
4
2
6
8
6
8
44681012 2
x
y
2
2
4
4
2
6
8
6
8
4646810 2
x
y

SECTION 10.2 Hyperbolas 699
In Exercises 33–38, identify the conic section whose equation
is given and use technology to graph it.
33. 2x
2
2y
2
12x 16y 26 0
34. 3x
2
3y
2
12x 6y 0
35. 2x
2
3y
2
12x 24y 54 0
36. x
2
2y
2
4x 4y 8
37. x
2
3y
2
4x 12y 20
38. 2x
2
16x y
2
6y 55
In Exercises 39–42, find the equation of the hyperbola that
satisfies the given conditions.
39. Center (2, 3); vertex (2, 1); passing through
(2 3 10, 11).
40. Center (5, 1); vertex (3, 1); passing through
(1, 1 4 3
).
41. Center (4, 2); vertex (7, 2); asymptote 3y 4x 10.
42. Center (3, 5); vertex (3, 0); asymptote 6y 5x 15.
In Exercises 43–48, determine which of the following equations
could possibly have the given graph.
(y
4
2)
2
(x
9
3)
2
1,
(x
3
3)
2
(y
4
3)
2
1,
4x
2
2y
2
8, 9(y 2)
2
36 4(x 3)
2
,
3(y 3)
2
4(x 3)
2
12, y
2
2x
2
6.
43.
44.
45.
46.
47.
48.
49. Sketch the graph of
y
4
2
x
b
2
2
1 for b 2, b 4, b 8,
b 12, and b 20. What happens to the hyperbola as b
takes larger and larger values? Could the graph ever degen-
erate into a pair of horizontal lines?
50. Find a number k such that (2, 1) is on the graph of
3x
2
ky
2
4. Then graph the equation.
51. Show that the asymptotes of the hyperbola
x
a
2
2
y
a
2
2
1 are
perpendicular to each other.
52. Find the approximate coordinates of the points where these
hyperbolas intersect:
(x
4
1)
2
(y
8
1)
2
1 and 4y
2
x
2
1.
53. Two listening stations that are 1 mile apart record an explo-
sion. One microphone receives the sound 2 seconds after
the other does. Use the line through the microphones as the
x-axis, with the origin midway between the microphones,
and the fact that sound travels at 1100 feet per second to
find the equation of a hyperbola on which the explosion
is located. Can you determine the exact location of the
explosion?
54. Two transmission stations P and Q are located 200 miles
apart on a straight shoreline. A ship 50 miles from shore is
moving parallel to the shoreline. A signal from Q reaches
the ship 400 microseconds after a signal from P
. If the sig-
nals travel at 980 feet per microsecond, find the location of
the ship (in terms of miles) in the coordinate system with
x-axis through P and Q and origin midway between them.
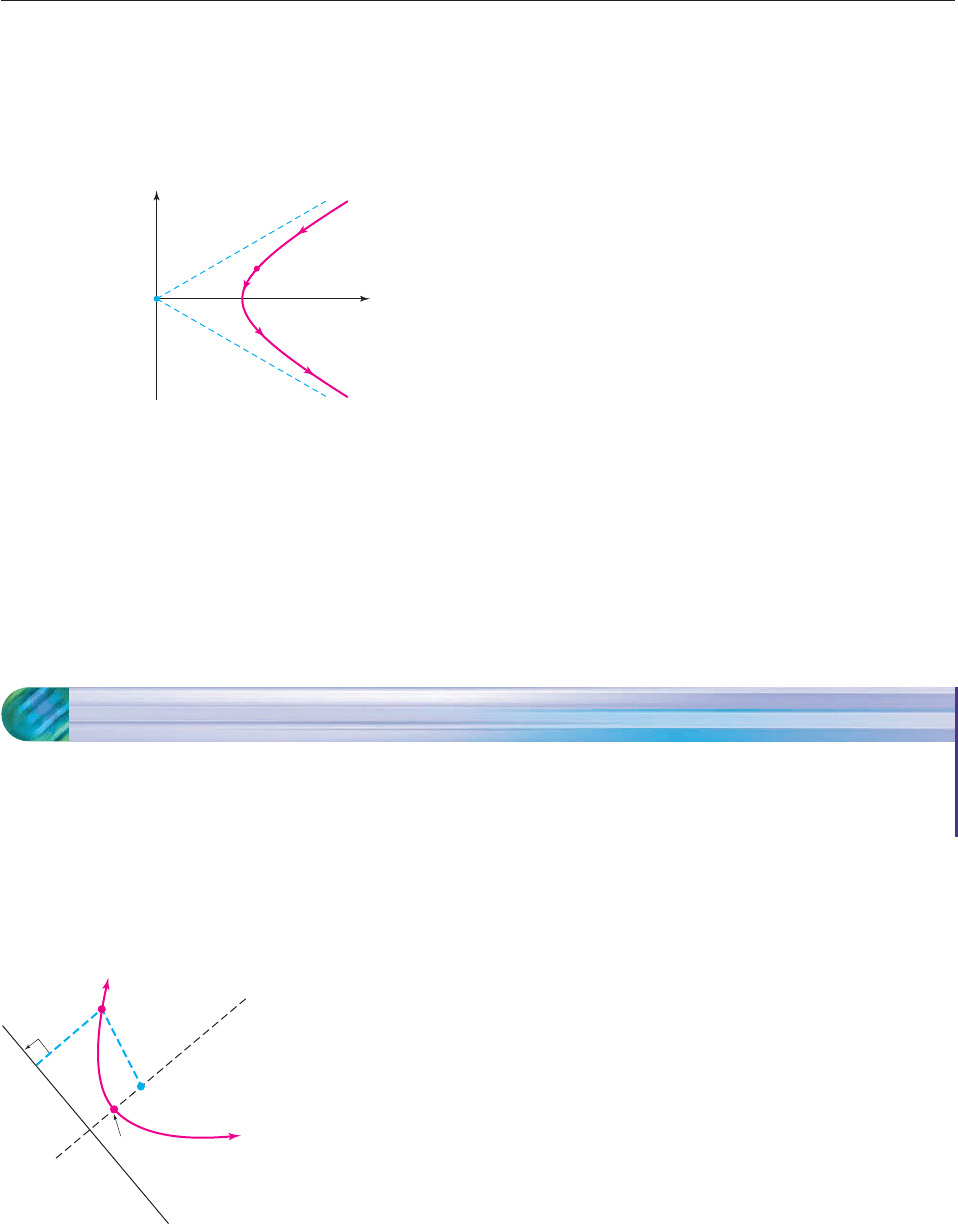
Exercises 55 and 56 deal with an experiment conducted by the
physicist Ernest Rutherford in 1911. Rutherford discovered that
when alpha particles are directed toward the nucleus of a gold
atom, the particles follow a hyperbolic path, as shown in the
figure, in which the nucleus is at the origin and the dashed
lines are the asymptotes of the particles path.
55. If the asymptotes of the hyperbolic path of the particle are
given by y
3
4
x and the closest the particle comes to the
nucleus is 5 units, find the equation of the particle’s path.
56. Do Exercise 55 when the asymptotes are y
2
3
x and the
minimum distance from the particle to the nucleus is 2 units.
Nucleus
Alpha particle
x
y
700 CHAPTER 10 Analytic Geometry
If a 0 and b 0, then the eccentricity of the hyperbola
(x
a
2
h)
2
(y
b
2
k)
2
1or
( y
a
2
k)
2
(x
b
2
h)
2
1
is the number
a
2
a
b
2
. In Exercises 57–61, find the eccen-
tricity of the hyperbola whose equation is given.
57.
(x
10
6)
2
4
y
0
2
1
58.
1
y
8
2
2
x
5
2
1
59. 6(y 2)
2
18 3(x 2)
2
60. 16x
2
9y
2
32x 36y 124 0
61. 4x
2
5y
2
16x 50y 71 0
62. (a) Graph these hyperbolas (on the same screen if
possible).
y
4
2
x
1
2
1
y
4
2
1
x
2
2
1
y
4
2
9
x
6
2
1
(b) Compute the eccentricity of each hyperbola in part (a).
(c) On the basis of parts (a) and (b), how is the shape of a
hyperbola related to its eccentricity?
10.3 Parabolas
■ Identify the focus, directrix, and standard equation of a parabola
and sketch its graph.
■ Set up and solve applied problems involving parabolas.
Definition. Parabolas appeared in Section 4.1 as the graphs of quadratic func-
tions. Parabolas of this kind are a special case of the following more general def-
inition. Let L be a line in the plane, and let P be a point not on L. If X is any point
not on L, the distance from X to L is defined to be the length of the perpendicular
line segment from X to L. The parabola with focus P and directrix L is the set of
all points X such that
Distance from X to P Distance from X to L
as shown in Figure 10–31.
The line through P perpendicular to L is called the axis. The intersection of
the axis with the parabola (the midpoint of the segment of the axis from P to L) is
the vertex of the parabola, as illustrated in Figure 10–31. The parabola is sym-
metric with respect to its axis.
Equation. Suppose that the focus is on the y-axis at the point (0, p), where p
is a nonzero constant, and that the directrix is the horizontal line y p. If (x, y)
is any point on the parabola, then the distance from (x, y) to the horizontal line
Section Objectives
Axis
Focus
Vertex
Directrix
X
P
L
Figure 10–31
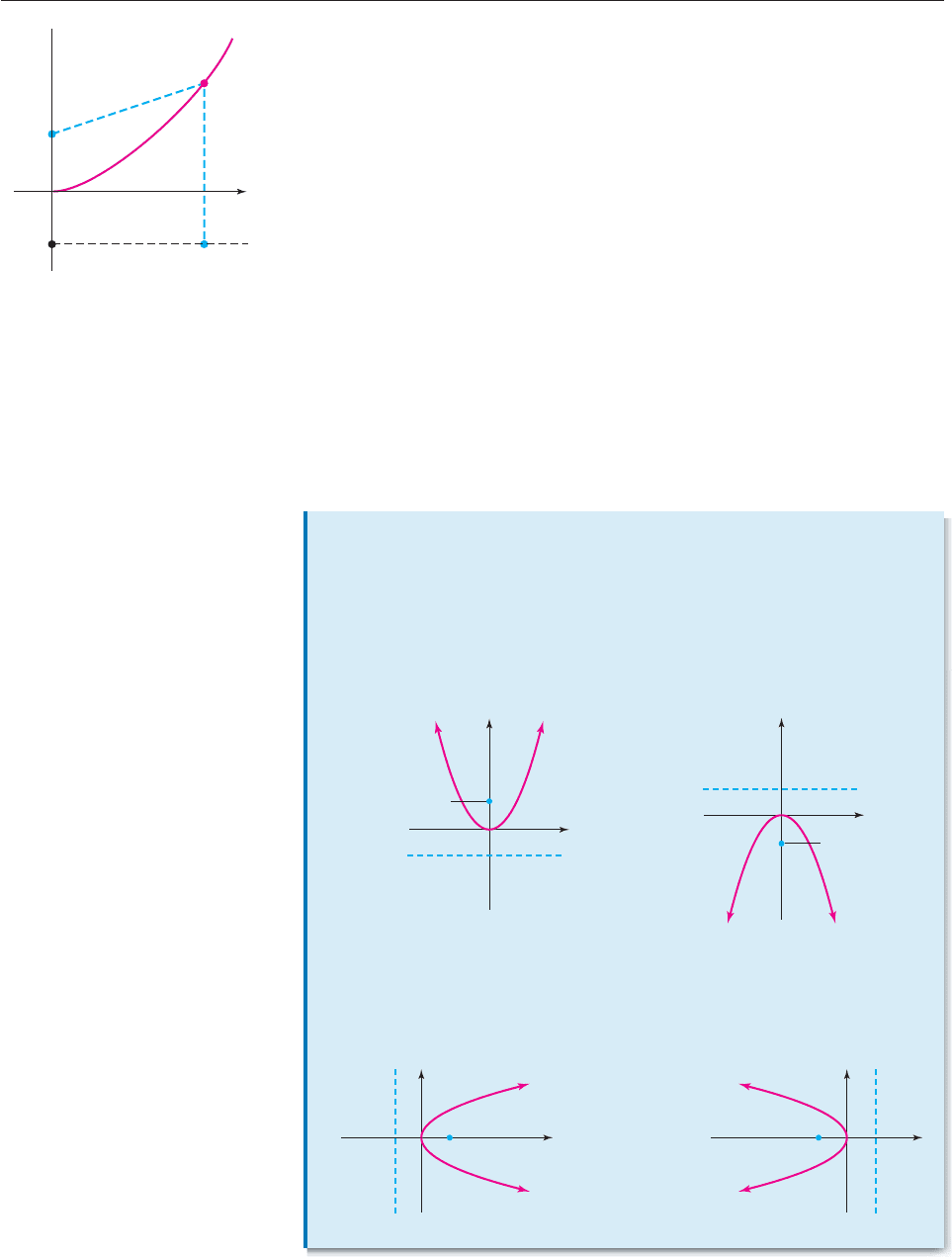
y p is the length of the vertical segment from (x, y) to (x, p) as shown in
Figure 10–32.
By the definition of the parabola,
Distance from (x, y) to (0, p) Distance from (x, y) to line y p
Distance from (x, y) to (0, p) Distance from (x, y) to (x, p)
(x 0
)
2
(
y p)
2
(x x
)
2
[
y (
p)]
2
.
Squaring both sides and simplifying, we have
(x 0)
2
(y p)
2
(x x)
2
(y p)
2
x
2
y
2
2py p
2
0
2
y
2
2py p
2
x
2
4py.
Conversely, it can be shown that every point whose coordinates satisfy this equa-
tion is on the parabola.
A similar argument works for the parabola with focus ( p, 0) on the x-axis and
directrix the vertical line x p. Furthermore, these arguments work for both
positive and negative p, and leads to this conclusion.
SECTION 10.3 Parabolas 701
(x, y)
(0, p)
(0, −p)
(x, −p)
x
Figure 10–32
Standard Equations
of Parabolas with
Vertex at the Origin
Let p be a nonzero real number. Then the graph of each of the following
equations is a parabola with vertex at the origin.
x
2
4py
focus: (0, p) directrix: y p axis: y-axis
p 0 p 0
opens upward opens downward
y
2
4px
focus: (p, 0) directrix: x p axis: x-axis
p 0 p 0
opens right opens left
Directrix
Focus
x
y
Directrix
Focus
x
y
Directrix
Focus
x
y
Directrix
Focus
x
y
EXAMPLE 1
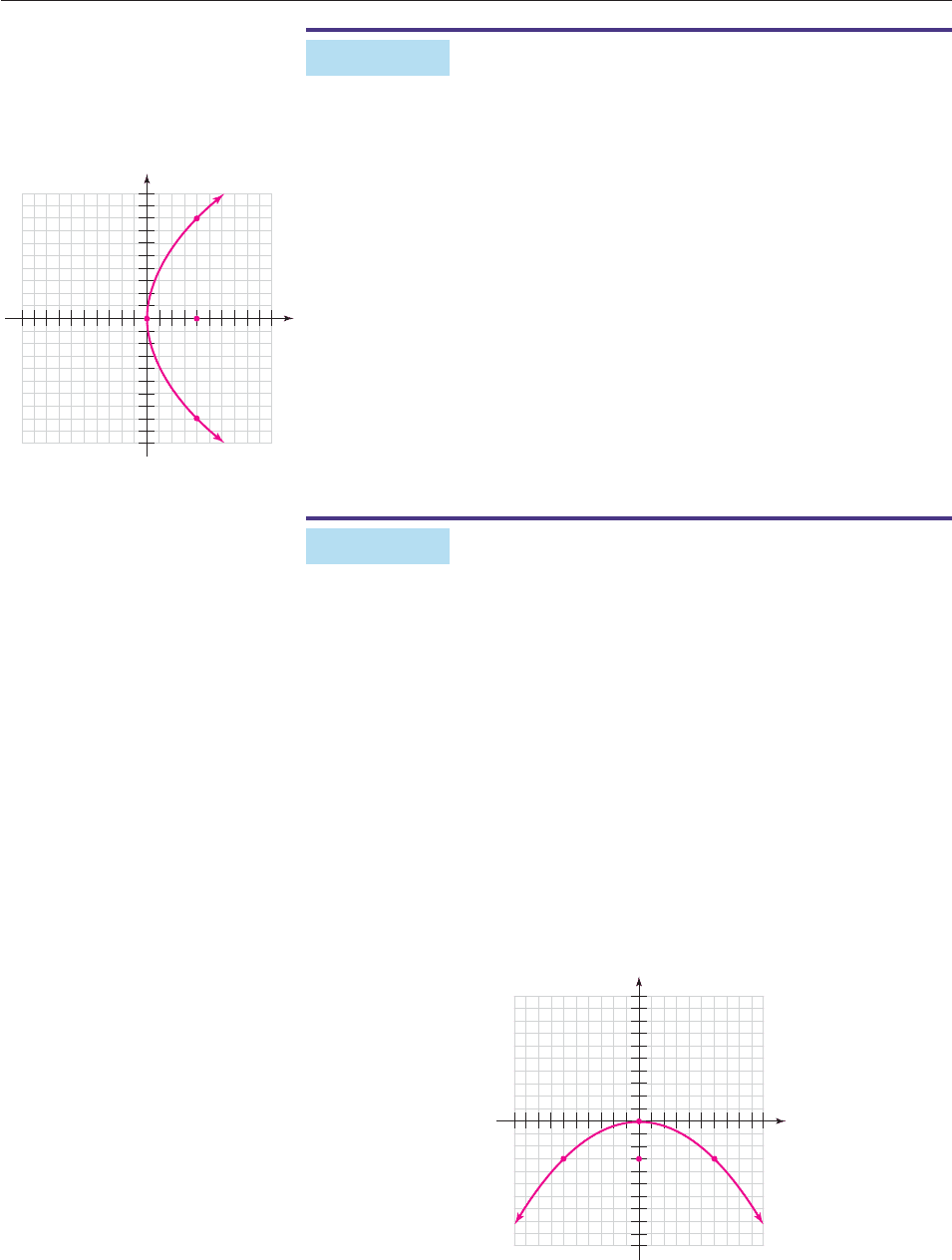
Find the equation of the parabola with vertex (0, 0) and focus (4, 0), and sketch its
graph.
SOLUTION Since the focus is (p, 0) (4, 0), we see that p 4 and that the
equation is
y
2
4px
4
4x 16x
Because p 4 0, the parabola opens to the right, as in the lower left-hand figure
in the preceding box. To get a reasonably accurate graph by hand we find the points
directly above and below the focus—that is, the points on the parabola with x 4.
y
2
16x
Let x 4: y
2
16
4 64
Take square roots: y 8
So we plot the points (4, 8) and (4, 8), and sketch the graph in Figure 10–33. ■
EXAMPLE 2
Find the equation of the parabola with vertex (0, 0) and focus (0, 3), and sketch
its graph.
SOLUTION The focus is (0, p) (0, 3), so p 3 and the equation is
x
2
4py 4(3)y 12y.
Since p 3 0, the parabola opens downward, as in the upper right-hand
figure in the preceding box. To sketch its graph we find the points to the left and
right of the focus (the points with y 3).
x
2
12y
Let y 3: x
2
12(3) 36
Take square roots: x 6
We plot the points (6, 3) and (6, 3), and sketch the graph in Figure 10–34.
■
702 CHAPTER 10 Analytic Geometry
2
2
4
4
2
6
10
8
6
10
8
46 10846108 2
x
y
Figure 10–33
2
2
4
4
2
6
10
8
6
10
8
46 10846108 2
x
y
Figure 10–34
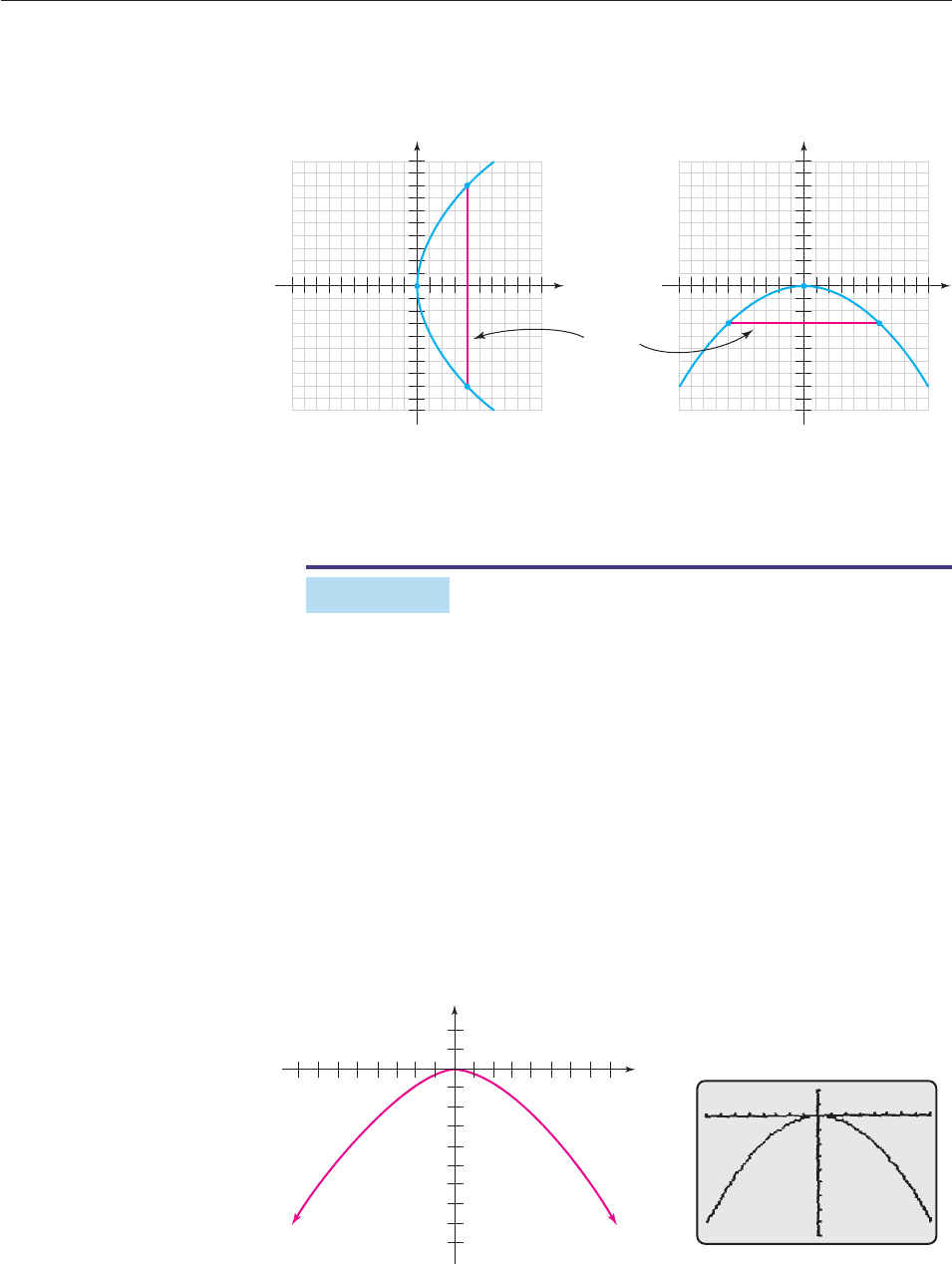
The line segment through the focus and perpendicular to the axis of a
parabola, with endpoints on the parabola, is called the latus rectum. In both
Example 1 and Example 2, the points we plotted to graph the parabola were the
endpoints of the latus rectum, as shown in Figure 10–35.
Figure 10–35
When graphing, the latus rectum can be thought of as indicating the “width” of a
parabola. Exercise 74 shows that the latus rectum is 4p units long when the equa-
tion of the parabola is x
2
4py or y
2
4px.
EXAMPLE 3
Show that the graph of x
2
8y 0 is a parabola. Find its focus, vertex, and
directrix, and sketch its graph.
SOLUTION We first rewrite the equation in standard form.
x
2
8y 0
Subtract 8y from both sides: x
2
8y
The last equation is in the standard form x
2
4py, with
4p 8
Divide both sides by 4: p 2
Hence, the graph is a downward-opening parabola with focus (0, 2) and vertex
(0, 0). The directrix is the horizontal line y p (2) 2. The graph can
be sketched by hand (Figure 10–36) or by rewriting the equation and using a cal-
culator (Figure 10–37). ■
Figure 10–36 Figure 10–37
2
8
9
8
–2
–1
1
–8 8
–4
–6
–8
x
y
x
2
=−8y
2
2
4
4
2
6
10
8
6
10
8
46 10
Latus
rectum
846108 2
x
y
2
2
4
4
2
6
10
8
6
10
8
46 10846108 2
x
y
SECTION 10.3 Parabolas 703
x
2
8y
y
x
8
2

EXAMPLE 4
Identify the graph of 3y
2
x and use technology to graph the equation.
SOLUTION We begin by rewriting the equation in standard form.
3y
2
x
Divide both sides by 3: y
2
3
x
y
2
1
3
x
This equation is in the standard form y
2
4px with
4p
1
3
Multiply both sides by
1
4
: p
1
1
2
So the graph is a parabola with focus (1/12, 0) and directrix x 1/12 that
opens to the right.
To sketch its graph, you can either use a conic section grapher*, or you can
solve the equation y
2
x/3 for y and graph the two resulting equations
y
3
x
and y
3
x
on the same screen. Both methods produce Figure 10–38. ■
EXAMPLE 5
Find the focus, directrix, and equation of the parabola that passes through the
point (8, 2), has vertex (0, 0) and focus on the x-axis.
SOLUTION Since the vertex is (0, 0) and the focus is on the x-axis, the equa-
tion is of the form y
2
4px. Since (8, 2) is on the graph, we have
y
2
4px
Let x 8 and y 2: 2
2
4p
8
4 32p
Divide both sides by 32: p
3
4
2
1
8
.
Therefore, the equation of the parabola is
y
2
4px
y
2
4
1
8
x
y
2
1
2
x.
Its graph is sketched in Figure 10–39. ■
704 CHAPTER 10 Analytic Geometry
−66
−4
4
Figure 10–38
–2
–1
1
2
468
x = 2y
2
x
y
2
Figure 10–39
*See the Technology Tip on page 681.

VERTICAL AND HORIZONTAL SHIFTS
We have seen that replacing x with x h and y with y k in the equation of an
ellipse or hyperbola shifts the graph vertically and horizontally. The same thing is
true for parabolas.
SECTION 10.3 Parabolas 705
Vertical and
Horizontal Shifts
Consider a parabola with equation
x
2
4py or y
2
4px.
Let h and k be constants. Replacing x with x h and replacing y with
y k in one of these equations produces the equation
(x h)
2
4p(y k)or(y k)
2
4p(x h),
whose graph is the original parabola shifted vertically and horizontally so
that its vertex is (h, k).
EXAMPLE 6
Identify and sketch the graph of (x 3)
2
8(y 4).
SOLUTION This equation can be obtained from the equation x
2
8y by re-
placing x with x 3 and replacing y with y 4. This is the situation described in
the preceding box, with h 3 and k 4. So the graph of (x 3)
2
8(y 4)
is a parabola with vertex (3, 4) that can be obtained from the parabola x
2
8y
(shown in Figure 10–36) by shifting it 3 units to the right and 4 units upward, as
shown in Figure 10–40. Its focus lies on the vertical line x 3. ■
Figure 10–40
EXAMPLE 7
Identify and sketch the graph of (y 3)
2
x
3
4
.
SOLUTION To use the information in the preceding box, we must rewrite the
equation in the form given there (x h, not x h, and similarly for the y term),
namely,
[y (3)]
2
1
3
[x (4)].
2
2
4
4
2
6
6
10
8
46 108468 2
x
y
