Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

height of the window at the center. [Hint: Use a coordinate
system, with the bottom of the window as the x-axis and the
vertical line through the center of the window as the y-axis.]
If a b 0, then the eccentricity of the ellipse
(x
a
2
h)
2
(y
b
2
k)
2
1or
(x
b
2
h)
2
(y
a
2
k)
2
1
is the number
a
2
a
b
2
. In Exercises 67–70, find the
eccentricity of the ellipse whose equation is given.
67.
1
x
0
2
0
9
y
9
2
1 68.
1
x
8
2
2
y
5
2
1
69.
(x
10
3)
2
(y
40
9)
2
1
70.
(x
12
5)
2
(y
8
4)
2
1
71. On the basis of your answers to Exercises 67–70, how is the
eccentricity of an ellipse related to its graph? [Hint: What is
the shape of the graph when the eccentricity is close to 0?
When it is close to 1?]
72. Assuming that these viewing windows are square, which of
these ellipses has the larger eccentricity?
(b)(a)
3 3
686 CHAPTER 10 Analytic Geometry
73. A satellite is to be placed in an elliptical orbit, with the cen-
ter of the earth as one focus. The satellite’s maximum dis-
tance from the surface of the earth is to be 22,380 km, and
its minimum distance is to be 6540 km. Assume that the
radius of the earth is 6400 km, and find the eccentricity of
the satellite’s orbit.
74. The first step in landing Apollo 11 on the moon was to place
the spacecraft in an elliptical orbit such that the minimum
distance from the surface of the moon to the spacecraft was
110 km and the maximum distance was 314 km. If the ra-
dius of the moon is 1740 km, find the eccentricity of the
Apollo 11 orbit.
75. Consider the ellipse whose equation is
x
a
2
2
y
b
2
2
1. Show
that if a b, then the graph is actually a circle.
76. Complete the derivation of the equation of the ellipse on
page 673 as follows.
(a) By squaring both sides, show that the equation
(x c
)
2
y
2
2a
(x c
)
2
y
2
may be simplified as
a
(x c
)
2
y
2
a
2
cx.
(b) Show that the last equation in part (a) may be further
simplified as
(a
2
c
2
)x
2
a
2
y
2
a
2
(a
2
c
2
).
THINKER
77. The punch bowl and a table holding the punch cups are
placed 50 feet apart at a garden party. A portable fence
is then set up so that any guest inside the fence can walk
straight to the table, then to the punch bowl, and then
return to his or her starting point without traveling more
than 150 feet. Describe the longest possible such fence
that encloses the largest possible area.
10.2 Hyperbolas
■ Find the vertices, foci and asymptotes of a hyperbola and sketch
its graph.
■ Set up and solve applied problems involving hyperbolas.
Definition. Let P and Q be points in the plane, and let r be a positive number.
The set of all points X such that
(Distance from P to X) (Distance from Q to X ) r
Section Objectives
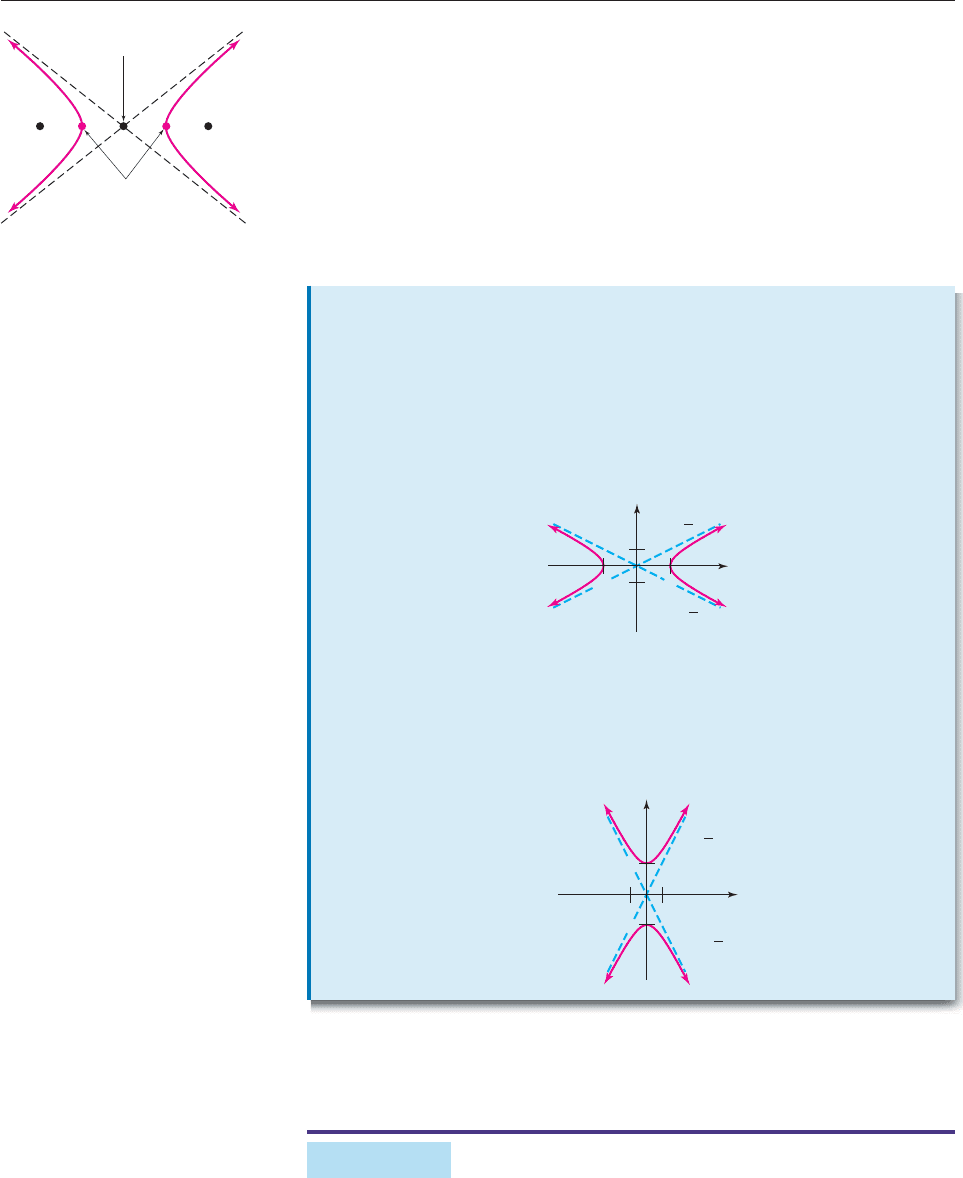
is the hyperbola with foci P and Q; r will be called the distance difference.
Every hyperbola has the general shape shown by the red curve in Figure 10–19.
The dotted straight lines are the asymptotes of the hyperbola; it gets closer and
closer to the asymptotes, but never touches them. The asymptotes intersect at
the midpoint of the line segment from P to Q; this point is called the center of the
hyperbola. The vertices of the hyperbola are the points where it intersects the line
segment from P to Q. The line through P and Q is called the focal axis.
Equation. A complicated exercise in the use of the distance formula, which
will be omitted here, leads to the following algebraic description.
SECTION 10.2 Hyperbolas 687
Vertices
Center
P
Q
Figure 10–19
Standard Equations
of Hyperbolas
Centered at
the Origin
Let a and b be positive real numbers. Then the graph of each of the follow-
ing equations is a hyperbola centered at the origin:
x-intercepts: ay-intercepts: none
focal axis on the x-axis, with vertices (a, 0) and (a, 0)
a
x
2
2
b
y
2
2
1
foci: (c, 0) and (c, 0), where c
a
2
b
2
.
asymptotes: y
b
a
x and y
b
a
x
x-intercepts: none y-intercepts: a
focal axis on the y-axis, with vertices (0, a) and (0, a)
y
a
2
2
x
b
2
2
1
foci: (0, c) and (0, c), where c
a
2
b
2
.
asymptotes: y
a
b
x and y
a
b
x
y
y = x
b
a
−b
b
a−a
x
y =− x
b
a
−b
b
x
a
−a
y
y =− x
a
b
y = x
a
b
Once again, don’t worry about all the letters in the box. The standard form of the
equation gives all the necessary information, as explained in the following example.
EXAMPLE 1
List the vertices, foci, and asymptotes of these hyperbolas.
(a)
2
x
5
2
1
y
6
2
1 (b)
y
4
2
1
x
6
2
1

SOLUTION
(a) We first rewrite the equation in standard form.
5
x
2
2
4
y
2
2
1
Now we can read off the required information. Because the hyperbola equa-
tion is of the form “x-term y-term,” the hyperbola opens from side to side
and its vertices (x-intercepts) are determined by the denominator of the x-term
of the equation: (5, 0) and (5, 0). To find the foci, we first compute c, which
is the square root of the sum of the denominators in the hyperbola’s equation:
c
a
2
b
2
5
2
4
2
25 1
6
41.
Hence, the foci are (41, 0) and (41, 0). Finally, to remember the cor-
rect asymptote coefficients, think of them as
4
5
.
So the asymptotes are
y
4
5
x and y
4
5
x.
(b) In standard form the equation is
2
y
2
2
4
x
2
2
1.
Because the hyperbola equation is of the form “y-term x-term,” the hyper-
bola opens up and down and its vertices (y-intercepts) are determined by the
denominator of the y-term of the equation: (0, 2) and (0, 2). The foci are
(0, c) and (0, c), where
c 2
2
4
2
4 16
20 25
.
Once again, the asymptote coefficients are
2
4
1
2
,
so the asymptotes are
y
1
2
x and y
1
2
x. ■
EXAMPLE 2
Identify and sketch the graph of the equation 9x
2
4y
2
36.
SOLUTION We first put the equation in standard form:
9x
2
4y
2
36
Divide both sides by 36:
9
3
x
6
2
4
3
y
6
2
3
3
6
6
Simplify:
x
4
2
y
9
2
1
x
2
2
2
y
3
2
2
1.
square root of the hyperbola’s y-term denominator
square root of the hyperbola’s x-term denominator
square root of the hyperbola’s y-term denominator
square root of the hyperbola’s x-term denominator
688 CHAPTER 10 Analytic Geometry
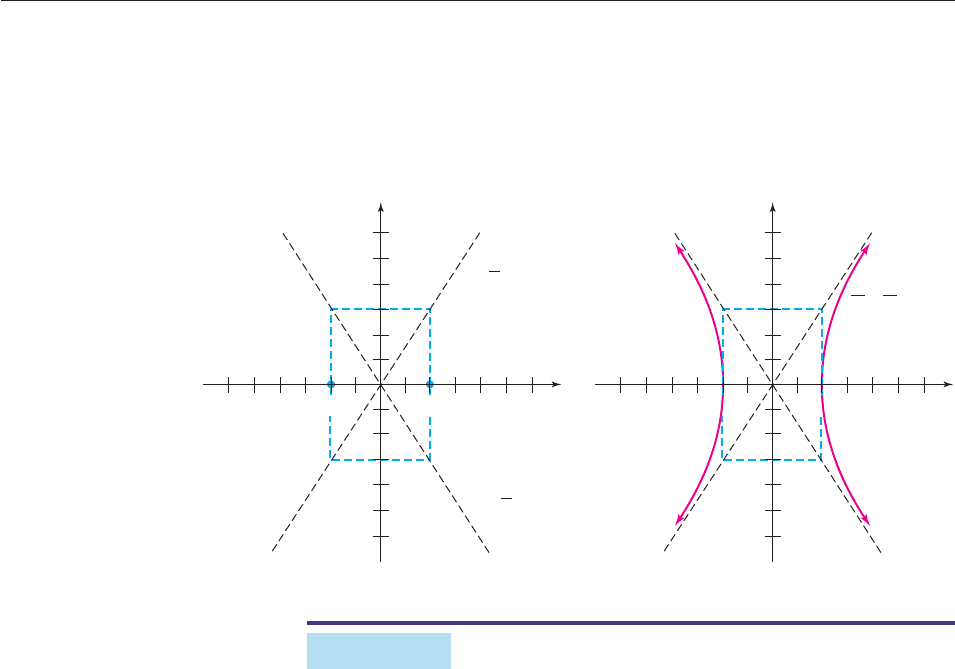
Applying the techniques of Example 1 or the facts in the preceding box (with
a 2 and b 3) shows that the graph is a hyperbola with vertices (2, 0) and
(2, 0) and asymptotes y
3
2
x and y
3
2
x. We first plot the vertices and sketch
the rectangle determined by the vertical lines x 2 and the horizontal lines
y 3. The asymptotes go through the origin and the corners of this rectangle,
as shown on the left in Figure 10–20. It is then easy to sketch the hyperbola. ■
Figure 10–20
EXAMPLE 3
Find the equation of the hyperbola with vertices (0, 1) and (0, 1) that passes
through the point (3, 2
). Then sketch its graph.
SOLUTION The vertices are on the y-axis, and the equation is of the form
a
y
2
2
x
b
2
2
1
with a 1. Since (3, 2
) is on the graph, we have
(
1
2
2
)
2
3
b
2
2
1
Simplify: 2
b
9
2
1
Subtract 2 from both sides:
b
9
2
1
Multiply both sides by b
2
: 9 b
2
.
Therefore, b 3, and the equation is
y
1
2
2
x
3
2
2
1 or, equivalently, y
2
x
9
2
1.
The asymptotes of the hyperbola are the lines y
1
3
x.
There are several ways to graph
y
1
2
3
x
2
2
1. You can graph by hand using
the technique of Example 2: Sketch the rectangle determined by the horizontal
lines y 1 and the vertical lines x 3. The asymptotes run through the origin
y =−
y = x
(2, 0)(–2, 0)
x
y
−= 1
x
2
4
3
2
x
3
2
(2, 0)(–2, 0)
x
y
y
2
9
SECTION 10.2 Hyperbolas 689

and the corners of this rectangle. Once you have these, it’s easy to plot a few
points and obtain the graph in Figure 10–21.
You can also use a calculator to graph the equation. A conic section grapher,
if your calculator has one, is the easiest way (Figure 10–22).* Otherwise, solve
the hyperbola equation for y:
y
2
x
9
2
1
Add
x
9
2
to both sides: y
2
1
x
9
2
Take square roots on both sides: y
1
x
9
2
or y
1
x
9
2
.
Graphing these last two equations on the same screen, also produces Figure 10–22.
■
Figure 10–21 Figure 10–22
VERTICAL AND HORIZONTAL SHIFTS
In Section 10.1 we saw that replacing x with x h and y with y k in the equa-
tion of an ellipse, shifts the ellipse vertically and horizontally. The same thing is
true for hyperbolas.
−6
9
6
−9
2468
2
2
4
6
6
4
4
6
8
x
y
690 CHAPTER 10 Analytic Geometry
*See the Technology Tip on page 681.
Vertical and
Horizontal Shifts
Consider a hyperbola centered at the origin with equation
a
x
2
2
b
y
2
2
1.
Let h and k be constants. Replacing x with x h and replacing y with
y k in this equation produces the equation
(x
a
2
h)
2
(y
b
2
k)
2
1,
whose graph is the original hyperbola shifted horizontally and vertically so
that its center is (h, k).
Analogous facts are true for the hyperbola with equation
a
y
2
2
b
x
2
2
1.
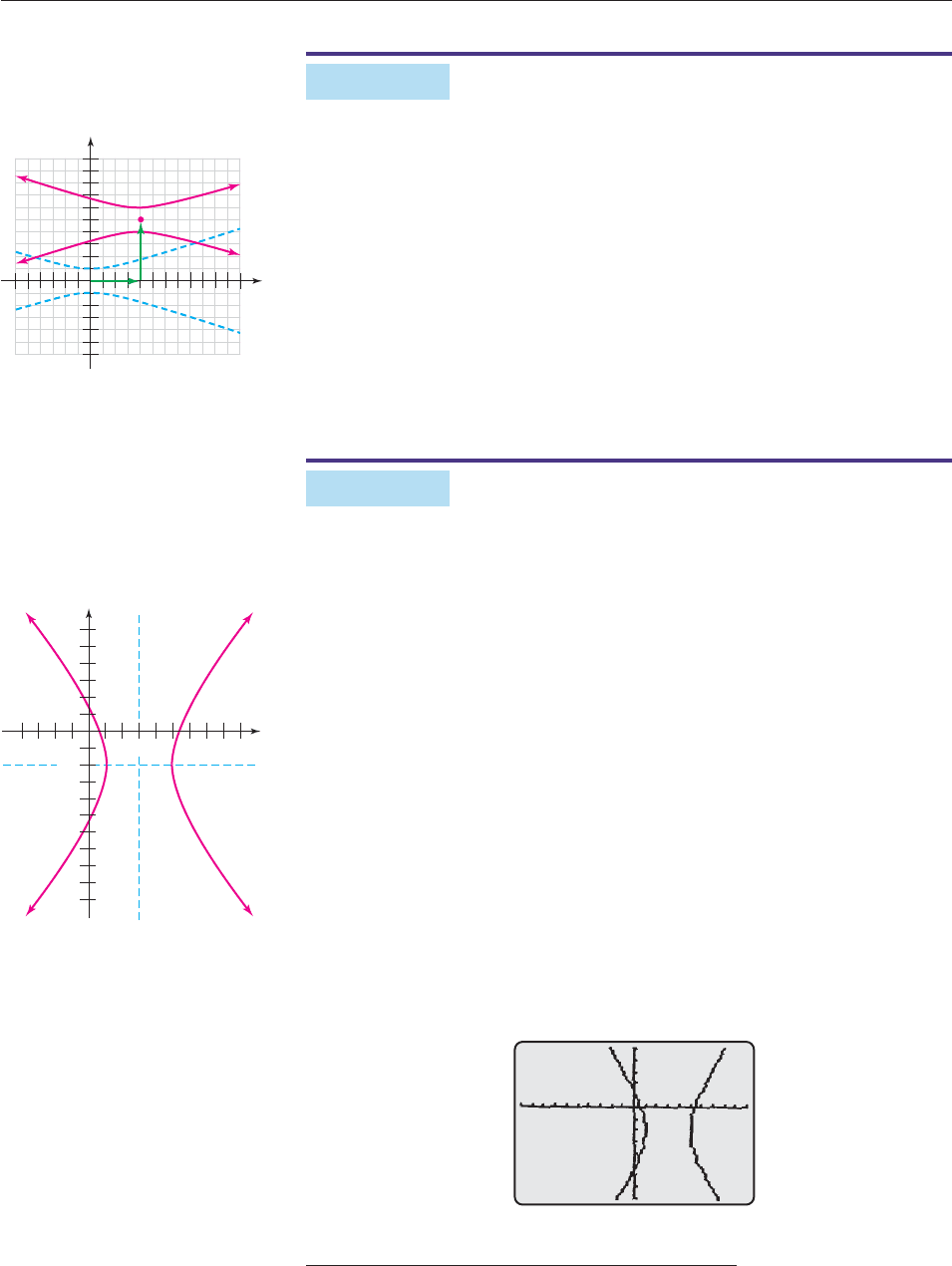
EXAMPLE 4
Identify and sketch the graph of
(y
1
5)
2
(x
9
4)
2
1.
SOLUTION This equation can be obtained from
y
1
2
x
9
2
1 by replacing x
with x 4 and replacing y with y 5. This is the situation described in the pre-
ceding box with h 4 and k 5. So the graph of
(y
1
5)
2
(x
9
4)
2
1 is a
hyperbola with center (4, 5). That can be obtained from the hyperbola
y
1
2
x
9
2
1
(shown in Figure 10–21) by shifting it 5 units upward and 4 units to the right, as
shown in Figure 10–23. Its vertices, foci and focal axis lie on the vertical line
x 4. ■
EXAMPLE 5
Identify and sketch the graph of
(x
4
3)
2
(y
9
2)
2
1.
SOLUTION If we rewrite the equation as
(x
2
2
3)
2
(y
3
(
2
2))
2
1,
then it has the form in the preceding box with h 3 and k 2. Its graph is a
hyperbola with center (3, 2). There are several ways to obtain the graph.
Method 1. The equation of this hyperbola can be obtained from
x
4
2
y
9
2
1
by replacing x with x 3 and y with y 2 y (2). So its graph is the hyperbola
x
4
2
y
9
2
1 (see Figure 10–20) shifted 3 units to the right and 2 units downward,
as shown in Figure 10–24. The vertices, foci, and focal axis lie on the horizontal
line y 2.
Method 2. If your calculator has a conic section grapher, you can insert the ap-
propriate values (a 2, b 3, h 3, and k 2) and obtain Figure 10–25.*
Figure 10–25
5
10
8
10
SECTION 10.2 Hyperbolas 691
5
4
x
y
Figure 10–23
3
−2
x
y
Figure 10–24
*See the Technology Tip on page 681.

Method 3. Solve the original equation for y:
(x
4
3)
2
(y
9
2)
2
1
Multiply both sides by 36: 9(x 3)
2
4(y 2)
2
36
Rearrange terms: 4(y 2)
2
9(x 3)
2
36
Divide both sides by 4: (y 2)
2
9(x 3
4
)
2
36
Take square roots of both sides: y 2
9(x
3
4
)
2
36
y 2
9(x
3
4
)
2
36
or y 2
9(x
3
4
)
2
36
.
EXAMPLE 6
Find the center, vertices, foci, and asymptotes of the hyperbola
(x
25
2)
2
(y
16
3)
2
1.
SOLUTION By writing x 2 as x (2), we see that the center of the hyper-
bola is (2, 3). Its graph is obtained from the hyperbola
2
x
5
2
1
y
6
2
1 by shifting
it 2 units to the left and 3 units upward. As shown in the box on page 687, the
vertices of
2
x
5
2
1
y
6
2
1 are (5, 0) and (5, 0). So the vertices of
(x
2
(
5
2))
2
(y
16
3)
2
1 are obtained as follows:
Shift 2 units left and
3 units upward
(5, 0)---------------------->(5 2, 0 3) (7, 3)
(5, 0)------------------------> (5 2, 0 3) (3, 3).
Similarly, the box on page 687 shows that the foci of
2
x
5
2
1
y
6
2
1 are
(c, 0) and (c, 0), where c 25 1
6
41. So the foci of
(x
2
(
5
2))
2
(y
16
3)
2
1 are given by:
Shift 2 units left and
3 units upward
(41, 0)---------------------->(41 2, 0 3) (41 2, 3)
(41, 0)------------------------->(41 2, 0 3) (41 2, 3).
692 CHAPTER 10 Analytic Geometry
Graph these last two equations in viewing window of Figure 10–24. How does your
graph compare with Figure 10–24? What is the explanation for the gaps?
GRAPHING EXPLORATION
■

The asymptotes of
2
x
5
2
1
y
6
2
1 are y
4
5
x. So the asymptotes of
(x
2
(
5
2))
2
(y
16
3)
2
1 are
y 3
4
5
(x (2)) and y 3
4
5
(x (2))
y
4
5
(x (2)) 3 y
4
5
(x (2)) 3
y
4
5
(x 2) 3 y
4
5
(x 2) 3. ■
Examples 4–6 illustrate the following facts.
SECTION 10.2 Hyperbolas 693
Standard Equations
of Hyperbolas
with Center at (h, k)
If a and b are positive real numbers, then the graph of each of the follow-
ing equations is a hyperbola with center (h, k).
focal axis on the horizontal line y k
foci: (c h, k) and (c h, k), where
(x
a
2
h)
2
( y
b
2
k)
2
1
c
a
2
b
2
vertices: (a h, k) and (a h, k)
asymptotes: y
b
a
(x h) k
focal axis on the vertical line x h
foci: (h, c k) and (h, c k), where
(y
a
2
k)
2
(x
b
2
h)
2
1
c
a
2
b
2
vertices: (h, a k) and (h, a k)
asymptotes: y
a
b
(x h) k
GRAPHING TECHNIQUES
When the equation of a hyperbola is in standard form, it can be graphed relatively
easily, either by hand or with technology, as illustrated in Examples 4 and 5. How-
ever, an equation can be graphed directly on a calculator or computer without first
putting it in standard form.
EXAMPLE 7
Sketch the graph of 6y
2
8x
2
24y 48x 96 0.
SOLUTION We first solve the equation for y. Begin by rewriting it as
6y
2
24y (8x
2
48x 96) 0.
This is a quadratic equation of the form ay
2
by c 0, with
a 6, b 24, c 8x
2
48x 96.
We use the quadratic formula to solve it.
y
b
2a
b
2
4
ac
y
y .
Now we graph both
y and
y
on the same screen to obtain the hyperbola in Figure 10–26. ■
Although the graph in Figure 10–26 shows you what the hyperbola looks
like, it does not provide all the pertinent information about the hyperbola. To get
that information, you do need to put the equation in standard form.
EXAMPLE 8
Find the center of the hyperbola in Example 7.
SOLUTION Begin by rearranging the equation.
6y
2
8x
2
24y 48x 96 0
Add 96 to both sides: 6y
2
24y 8x
2
48x 96
Group x- and y-terms: (6y
2
24y) (8x
2
48x) 96
Factor out coefficients of y
2
and x
2
: 6(y
2
4y) 8(x
2
6x) 96.
Complete the square in the expression y
2
4y by adding 4 (the square of half the
coefficient of y), and complete the square in x
2
6x by adding 9 (the square of
half the coefficient of x).
6(y
2
4y 4) 8(x
2
6x 9) 96 ? ?
On the left side, we have actually added 6
4 24 and 8
9 72, so we must
add these numbers on the right to keep the equation unchanged.
6(y
2
4y 4) 8(x
2
6x 9) 96 24 72
Factor and simplify: 6(y 2)
2
8(x 3)
2
48
Divide both sides by 48:
(y
8
2)
2
(x
6
3)
2
1
(y
8
2)
2
(x (
6
3))
2
1.
In this form, we can see that the graph is a hyperbola with center at (3, 2). ■
24
576
24(8
x
2
4
8x 9
6)
12
24
576
24(8
x
2
4
8x 9
6)
12
24
576
24(8
x
2
4
8x 9
6)
12
(24)
(24)
2
4
6(8x
2
48
x 96
)
2
6
694 CHAPTER 10 Analytic Geometry
−6
12
10
−12
Figure 10–26
NOTE
Parametric equations for hyperbolas
are discussed in Special Topics 10.3.A
and summarized in the endpapers at
the beginning of the book.
CAUTION
Completing the square only works
when the coefficient of y
2
is 1. In an
expression such as 6y
2
24y, you
must first factor out the 6,
6(y
2
4y),
and then complete the square on the
expression in parentheses.
APPLICATIONS
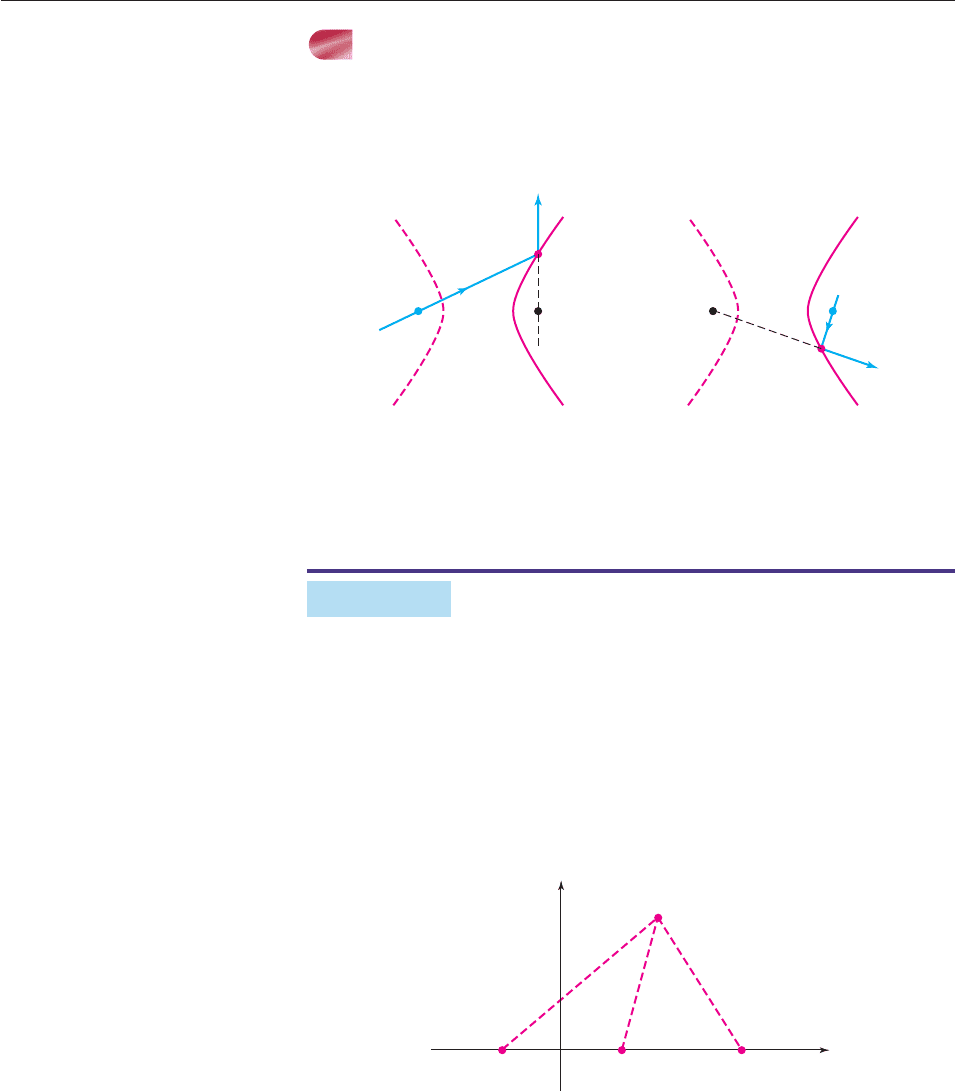
The reflective properties of hyperbolas are used in the design of camera and tele-
scope lenses. If a light ray passes through one focus of a hyperbola and reflects off
the hyperbola at a point P, then the reflected ray moves along the straight line
determined by P and the other focus, as shown in Figure 10–27.
Figure 10–27
Hyperbolas are also the basis of the long-range navigation system (LORAN),
which enables a ship to determine its exact location by radio, as illustrated in the
next example.
EXAMPLE 9
Three LORAN transmitters Q, P, and R are located 200 miles apart along a
straight shoreline and simultaneously transmit signals at regular intervals. These
signals travel at a speed of 980 feet per microsecond. A ship S receives a signal
from P and 305 microseconds later a signal from R. It also receives a signal from Q
528 microseconds after the one from P. Determine the ship’s location.
SOLUTION Take the line through the LORAN stations as the x-axis, with the
origin located midway between Q and P, so that the situation looks like Fig-
ure 10–28.
Figure 10–28
If the signal takes t microseconds to go from P to S, then
d
1
980t and d
2
980(t 528),
so
d
1
d
2
980t 980(t 528) 980
528 517,440 feet.
x
y
Q
PR
−100 100 300
S
d
2
d
3
d
1
Focus
Focus
P
Focus
Focus
P
SECTION 10.2 Hyperbolas 695
