Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

SOLUTION Apply the formula in the box above with u 3, 1 and
v 5, 2.
cos u
.
Using the COS
1
key, we see that
u 2.4393 radians ( 139.76°). ■
The Angle Theorem has several useful consequences. For instance, by taking
absolute values on both sides of u
v uv cos u and using the fact that
uv uv (because uv 0), we see that
u
v uv cos u uv cos u uvcos u.
But for any angle u, cos u 1, so
u
v uvcos u uv.
This proves the Schwarz inequality.
Vectors u and v are said to be orthogonal (or perpendicular) if the angle be-
tween them is p/2 radians (90°), or if at least one of them is 0. Here is the key fact
about orthogonal vectors.
Proof If u or v is 0, then u
v 0, and if u and v are nonzero orthogonal vec-
tors, then by the Angle Theorem,
u
v uv cos u uv cos(p/2) uv (0) 0.
Conversely, if u and v are vectors such that u
v 0, then Exercise 42 shows that
u and v are orthogonal. ■
EXAMPLE 4
(a) The vectors u 2, 6 and v 9, 3 are orthogonal because
u
v 2, 6
9, 3 2
9 (6)3 18 18 0.
(b) The vectors
1
2
i 5j and 10i j are orthogonal, since
1
2
i 5j
(10i j)
1
2
(10) 5(1) 5 5 0. ■
13
290
13
1029
(3)5 1
2
(3)
2
1
2
5
2
2
2
u
v
uv
656 CHAPTER 9 Applications of Trigonometry
Schwarz
Inequality
For any vectors u and v,
u
v uv.
Orthogonal
Vectors
Let u and v be vectors. Then
u and v are orthogonal exactly when u
v 0.
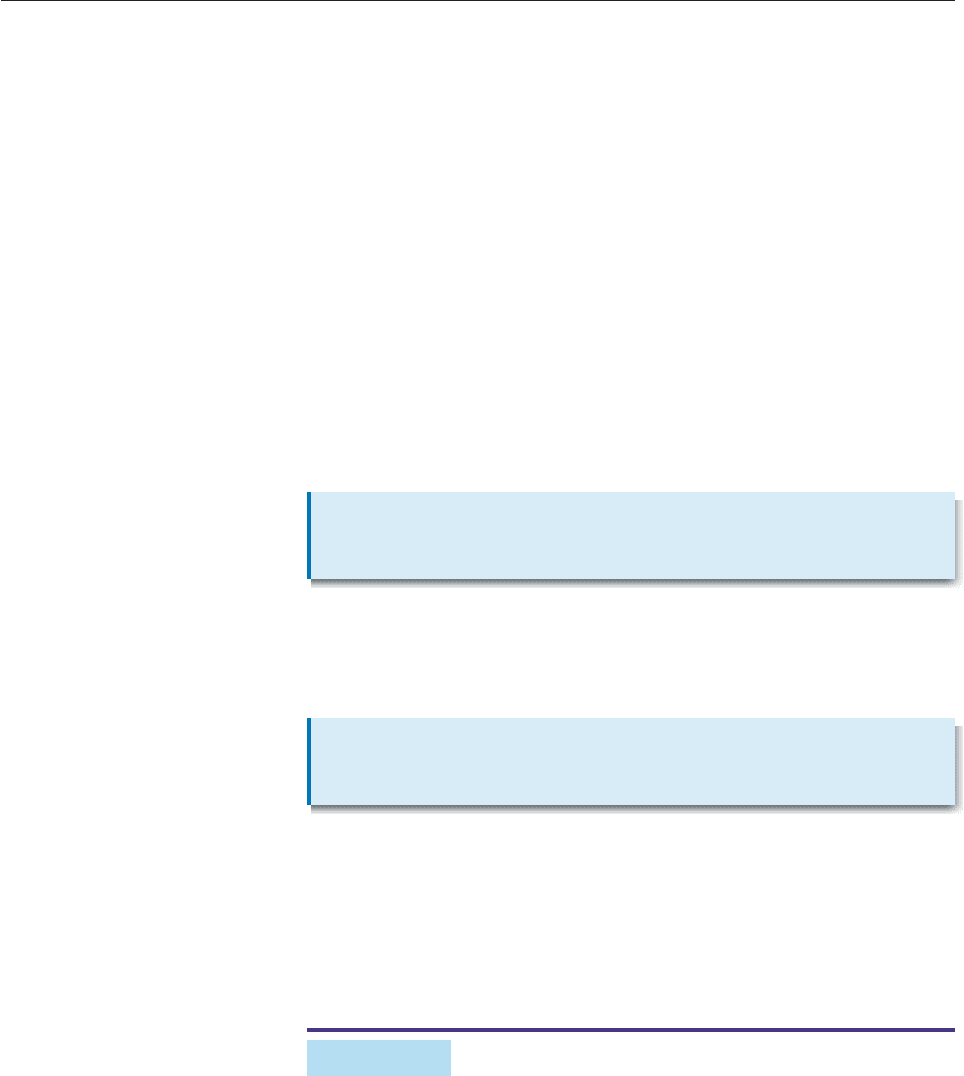
PROJECTIONS AND COMPONENTS
If u and v are nonzero vectors and u is the angle between them, construct the per-
pendicular line segment from the terminal point P of u to the straight line on
which v lies. This perpendicular segment intersects the line at a point Q, as shown
in Figure 9–25.
Figure 9–25
The vector OQ
is called the projection of u on v and is denoted proj
v
u. Here is a
useful description of proj
v
u.
Proof Since proj
v
u and v lie on the same straight line, they are parallel, and
hence, proj
v
u kv for some real number k. Let w be the vector with initial point
at the origin and the same length and direction as QP
, as in the two cases shown
in Figure 9–26.
Figure 9–26
Note that w is parallel to QP
and hence is orthogonal to v. As is shown in Fig-
ure 9–26, u proj
v
u w kv w. Consequently, by the properties of the dot
product,
u
v (kv w)
v (kv)
v w
v
k(v
v) w
v kv
2
w
v.
But w
v 0 because w and v are orthogonal. Hence,
u
v kv
2
or, equivalently, k .
u
v
v
2
v
w
u
O
Q
Q
proj
v
u
P
v
w
u
O
proj
v
u
P
v
u
Q
P
O
v
u
Q
P
O
v
u
Q
P
O
SECTION 9.4 The Dot Product 657
Projection of
u on v
If u and v are nonzero vectors, then the projection of u on v is the vector
proj
v
u
v.
u
v
v
2

Therefore,
proj
v
u kv
v,
and the proof is complete. ■
EXAMPLE 5
If u 8i 3j and v 4i 2j, find proj
v
u and proj
u
v.
SOLUTION
u
v 8
4 3(2) 26, and v
2
v
v 4
2
(2)
2
20.
Therefore,
proj
v
u
v
2
2
6
0
(4i 2j)
2
5
6
i
1
5
3
j,
as is shown in Figure 9–27. We can find the projection of v on u by noting that
u
2
u
u 8
2
3
2
73, and hence,
proj
u
v
u
2
7
6
3
(8i 3j)
2
7
0
3
8
i
7
7
8
3
j. ■
Figure 9–27
Recall that
1
v
v is a unit vector in the direction of v (see page 646). We can
express proj
v
u as a scalar multiple of this unit vector as follows.
proj
v
u
v
1
v
v
.
The scalar is called the component of u along v and is denoted comp
v
u.
Thus,
proj
v
u
v
comp
v
u
1
v
v
.
Since
1
v
v is a unit vector, the length of proj
v
u is
proj
v
u
comp
v
u
1
v
v
comp
v
u
1
v
v
comp
v
u.
1
v
u
v
v
u
v
v
u
v
v
u
v
v
2
u
v
x
y
proj
u
v
proj
v
u
v
u
u
2
u
v
v
2
u
v
v
2
658 CHAPTER 9 Applications of Trigonometry
Furthermore, since u
v uv cos u, where u is the angle between u and v, we
have
comp
v
u
uv
v
cos u
.
Cancelling v on the right side produces this result.
EXAMPLE 6
If u 2i 3j and v 5i 2j, find comp
v
u and comp
u
v.
SOLUTION
comp
v
u .
comp
u
v
1
4
3
. ■
APPLICATIONS
Vectors and the dot product can be used to solve a variety of physical problems.
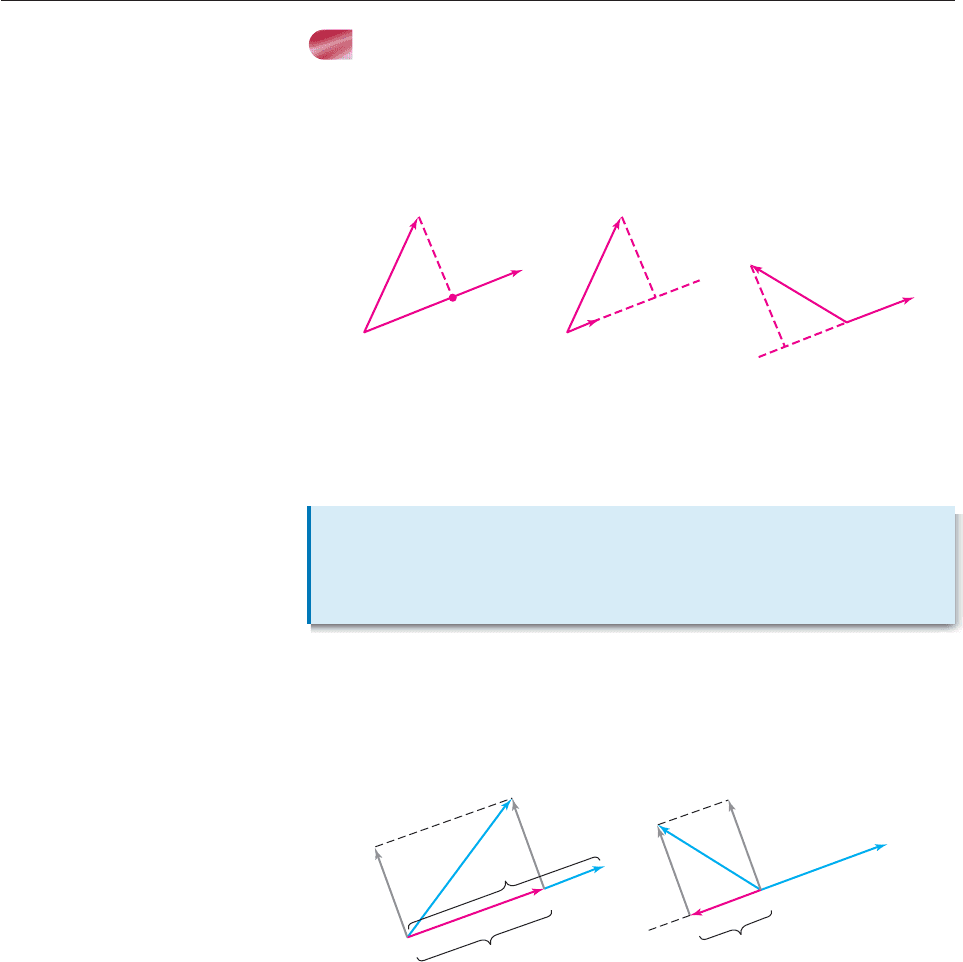
EXAMPLE 7
A 4000-pound automobile is on an inclined ramp that makes a 15° angle with the
horizontal. Find the force required to keep it from rolling down the ramp, assum-
ing that the only force that must be overcome is that due to gravity.
SOLUTION The situation is shown in Figure 9–28, where the coordinate sys-
tem is chosen so that the car is at the origin, the vector F representing the down-
ward force of gravity is on the y-axis, and v is a unit vector from the origin down
the ramp. Since the car weighs 4000 pounds, F 4000j. Figure 9–28 shows
that the angle between v and F is 75°. The vector proj
v
F is the force pulling the
car down the ramp, so a force of the same magnitude in the opposite direction is
needed to keep the car motionless. As we saw in the preceding box,
proj
v
F comp
v
F F cos 75°
4000(.25882) 1035.3.
Therefore, a force of 1035.3 pounds is required to hold the car in place. ■
4
2
2
3
2
v
u
u
4
29
2(5) 3
2
(5)
2
2
2
u
v
v
u
v
v
SECTION 9.4 The Dot Product 659
Projections
and Components
If u and v are nonzero vectors and u is the angle between them, then
comp
v
u u cos u
and
proj
v
u comp
v
u.
u
v
v
x
y
15°
15°
75°
Ramp
proj
v
F
F
v
Figure 9–28
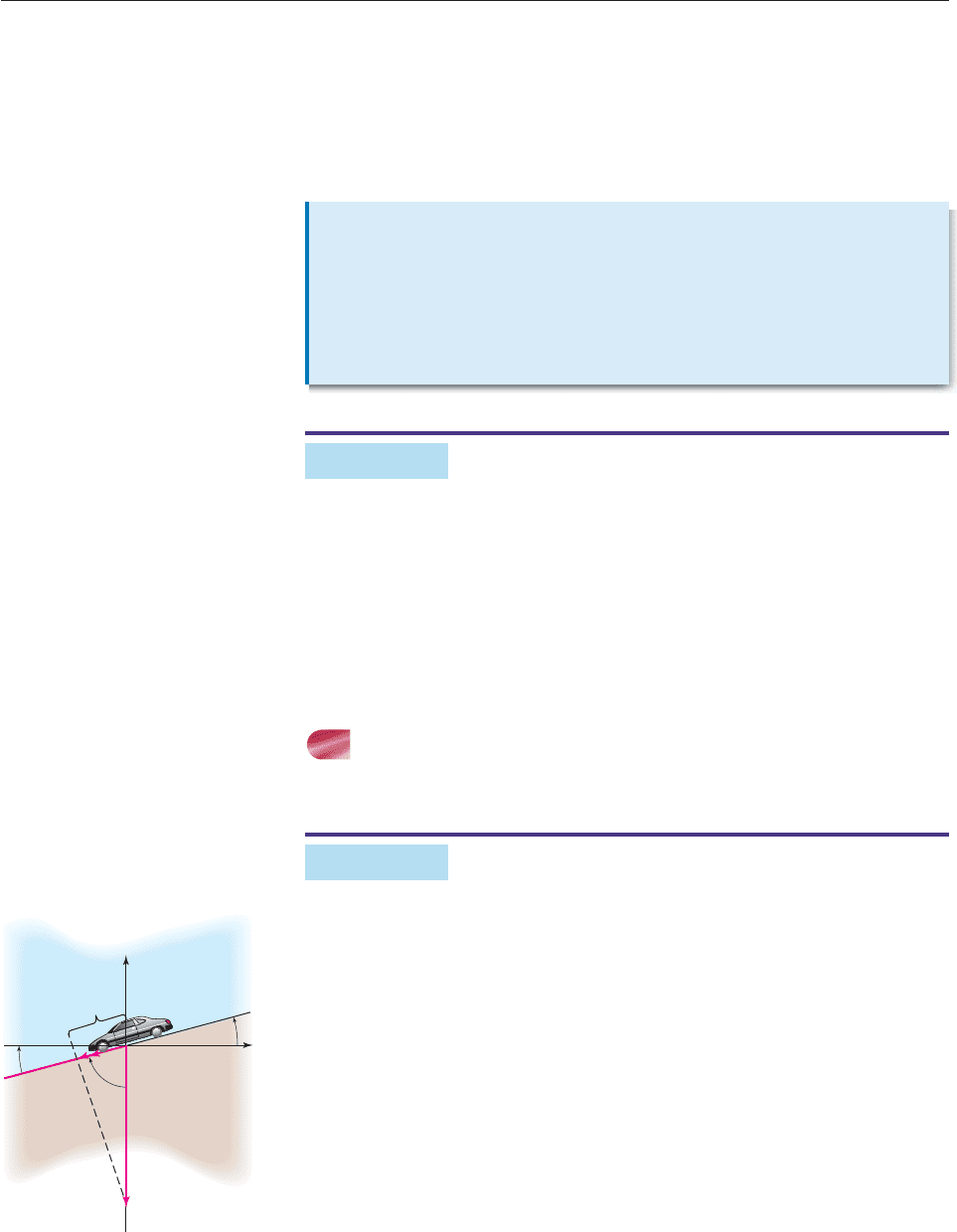
If a constant force F is applied to an object, pushing or pulling it a distance d
in the direction of the force as shown in Figure 9–29, the amount of work done by
the force is defined to be the product
W (magnitude of force)(distance) F
d.
If the magnitude of F is measured in pounds and d in feet, then the units for
W are foot-pounds. For example, if you push a car for 35 feet along a level drive-
way by exerting a constant force of 110 pounds, the amount of work done is
110
35 3850 foot-pounds.
When a force F moves an object in the direction of a vector d rather than in the
direction of F, as shown in Figure 9–30, then the motion of the object can be con-
sidered as the result of the vector proj
d
F, which is a force in the same direction as d.
Therefore, the amount of work done by F is the same as the amount of work
done by proj
d
F, namely,
W (magnitude of proj
d
F)(length of d) proj
d
F
d.
The box on page 659 and the Angle Theorem (page 655) show that
W proj
d
F
d comp
d
F
d
F(cos u)d
F
d.*
Consequently, we have these descriptions of work.
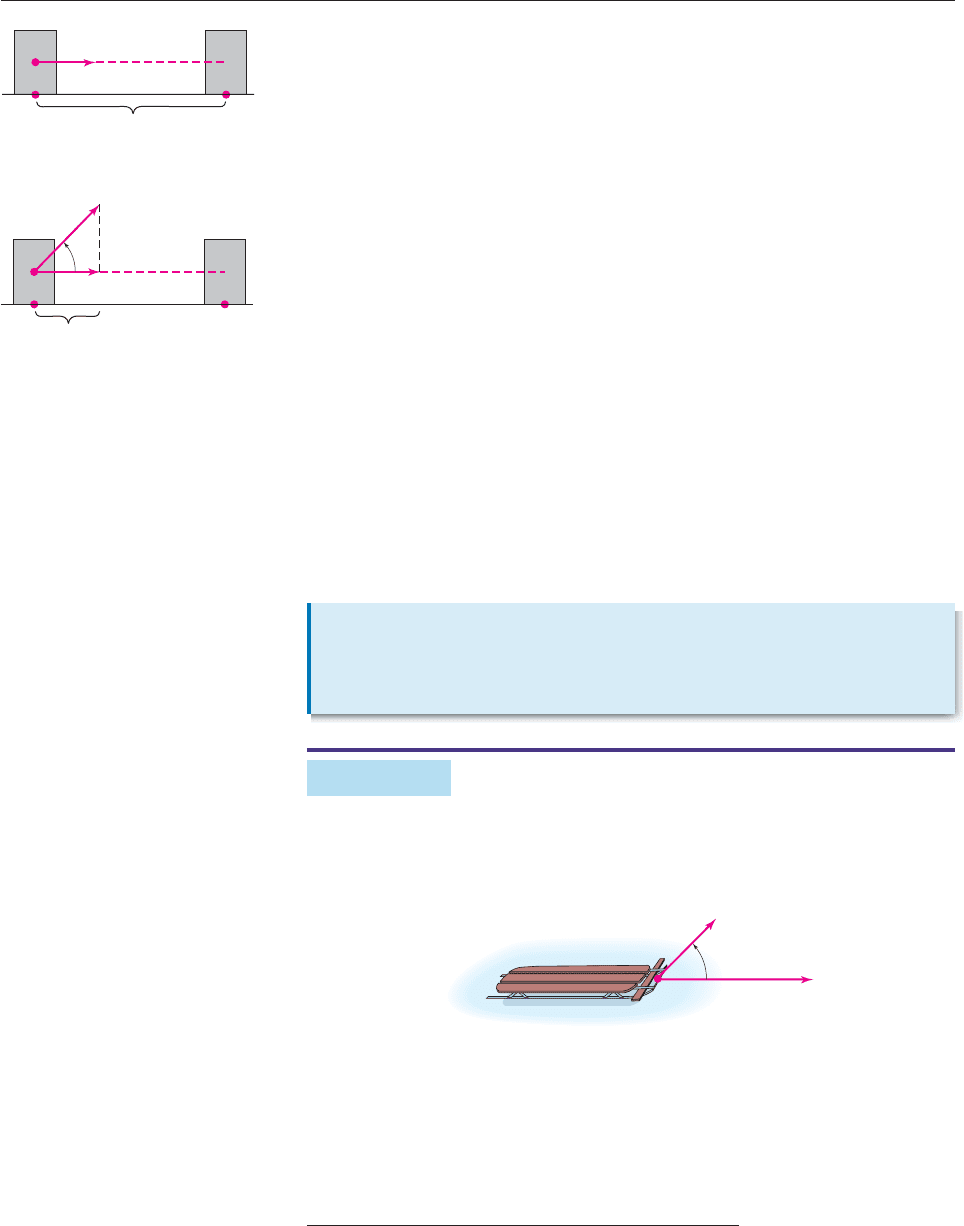
EXAMPLE 8
How much work is done by a child who pulls a sled 100 feet over level ground by
exerting a constant 20-pound force on a rope that makes a 45° angle with the
ground?
Figure 9–31
SOLUTION The situation is shown in Figure 9–31, where the force F on the rope
has magnitude 20 and the sled moves along vector d of length 100. The work done is
W F
d Fd
cos u 20
100
2
2
1000 2
1414.2 foot-pounds. ■
F
d
45°
660 CHAPTER 9 Applications of Trigonometry
F
d
Figure 9–29
F
d
θ
proj
d
F
Figure 9–30
Work
The work W done by a constant force F as its point of application moves
along the vector d is
W comp
u
F
d or, equivalently, W F
d.
*This formula reduces to the previous one when F and d have the same direction because in that case,
cos u cos 0 1, so W F
d (magnitude of force)(distance moved).

SECTION 9.4 The Dot Product 661
EXERCISES 9.4
In Exercises 1–6, find u
v, u
u, and v
v.
1. u 3, 4, v 5, 2
2. u 1, 6, v 4, 1/3
3. u 2i j, v 3i
4. u i j, v 5j
5. u 3i 2j, v 2i 3j
6. u 4i j, v i 2j
In Exercises 7–12, find the dot product when u 4, 3,
v 5, 2, and w 4, 1.
7. u
(v w)
8. u
(v w)
9. (u v)
(v w)
10. (u v)
(u v)
11. (3u v)
(2w)
12. (u 4v)
(2u w)
In Exercises 13–18, find the angle between the two vectors.
13. 4, 3, 1, 2
14. 2, 4, 0, 5
15. 2i 3j, i
16. 2j, 4i j
17. 2
i 2
j, i j
18. 3i 5j, 2i 3j
In Exercises 19–24, determine whether the given vectors are
parallel, orthogonal, or neither.
19. 2, 6, 3, 1
20. 5, 3, 2, 6
21. 9, 6, 6, 4
22. i 2j, 2i 4j
23. 2i 2j, 5i 8j
24. 6i 4j, 2i 3j
In Exercises 25–28, find a real number k such that the two vec-
tors are orthogonal.
25. 2i 3j, 3i kj
26. 3i j, 2ki 4j
27. i j, ki 2
j
28. 4i 5j, 2i 2kj
In Exercises 29–32, find proj
u
v and proj
v
u.
29. u 3i 5j, v 6i 2j
30. u 2i 3j, v i 2j
31. u i j, v i j
32. u 5i j, v 2i 3j
In Exercises 33–36, find comp
v
u.
33. u 10i 4j, v 3i 2j
34. u i 2j, v 3i j
35. u 3i 2j, v i 3j
36. u i j, v 3i 2j
In Exercises 37–39, let u a, b, v c, d, and w r, s.
Verify that the given property of dot products is valid by calcu-
lating the quantities on each side of the equal sign.
37. u
(v w) u
v u
w
38. ku
v k(u
v) u
kv
39. 0
u 0
40. Suppose u a, b and v c, d are nonzero parallel
vectors.
(a) If c 0, show that u and v lie on the same nonvertical
straight line through the origin.
(b) If c 0, show that v u (that is, v is a scalar mul-
tiple of u). [Hint: The equation of the line on which u
and v lie is y mx for some constant m (why?), which
implies that b ma and d mc.]
(c) If c 0, show that v is a scalar multiple of u. [Hint: If
c 0, then a 0 (why?), and hence, b 0 (otherwise,
u 0).]
41. Prove the Angle Theorem in the case when u is 0 or p.
42. If u and v are nonzero vectors such that u
v 0, show that
u and v are orthogonal. [Hint: If u is the angle between u
and v, what is cos u and what does this say about u?]
43. Show that (1, 2), (3, 4), (5, 2) are the vertices of a right tri-
angle by considering the sides of the triangle as vectors.
44. Find a number x such that the angle between the vectors
1, 1 and x, 1 is p/4 radians.
45. Find nonzero vectors u, v, and w such that u
v u
w and
v w and neither v nor w is orthogonal to u.
46. If u and v are nonzero vectors, show that the vectors
uv vu and uv vu are orthogonal.
47. A 600-pound trailer is on an inclined ramp that makes a 30°
angle with the horizontal. Find the force required to keep it
from rolling down the ramp, assuming that the only force
that must be overcome is that due to gravity.
48. In Example 7, find the vector that represents the force nec-
essary to keep the car motionless.
a
c

662 CHAPTER 9 Applications of Trigonometry
In Exercises 49–52, find the work done by a constant force F
as the point of application of F moves along the vector PQ
.
49. F 2i 5j, P (0, 0), Q (4, 1)
50. F i 2j, P (0, 0), Q (5, 2)
51. F 2i 3j, P (2, 3), Q (5, 9) [Hint: Find the compo-
nent form of PQ
.]
52. F 5i j, P (1, 2), Q (4, 3)
53. A lawn mower handle makes an angle of 60° with the
ground. A woman pushes on the handle with a force of
30 pounds. How much work is done in moving the lawn
mower a distance of 75 feet on level ground?
54. A child pulls a wagon along a level sidewalk by exerting a
force of 18 pounds on the wagon handle, which makes an
angle of 25° with the horizontal. How much work is done in
pulling the wagon 200 feet?
55. A 40-pound cart is pushed 100 feet up a ramp that makes a
20° angle with the horizontal (see the figure). How much
work is done against gravity? [Hint: The amount of work
done against gravity is the negative of the amount of work
done by gravity. Coordinatize the situation so that the
cart is at the origin. Then the cart moves along vector
d (100 cos 20°)i (100 sin 20°)j, and the downward
force of gravity is F 0i 40j.]
56. Suppose the child in Exercise 54 is pulling the wagon up a
hill that makes an angle of 20° with the horizontal and all
other facts remain the same. How much work is done in
pulling the wagon 150 feet?
20°
Chapter 9 Review
IMPORTANT CONCEPTS
Section 9.1
Complex plane 626
Real axis 626
Imaginary axis 626
Absolute value 627
Modulus 627
Argument 627
Polar form 627
Multiplication and division in polar
form 629
Section 9.2
DeMoivre’s Theorem 632
Formula for nth roots 635
Roots of unity 636
Section 9.3
Vector 640
Magnitude 640–641
Components 641
Scalar multiplication 642
Vector addition and subtraction
643–645
Unit vector 645–646
Linear combination of i and j 646
Direction angle of a vector
647
Section 9.4
Dot product 653
Angle between vectors 654
Parallel vectors 655
Angle Theorem 655
Schwarz inequality 656
Orthogonal vectors 656
Projection of u on v 657
Component of u along v 658–659
Work 660
IMPORTANT FACTS & FORMULAS
■
a bi
a
2
b
2
■
a bi r(cos u i sin u), where
r
a
2
b
2
, a r cos u, b r sin u.

CHAPTER 9 Review 663
■
r
1
(cos u
1
i sin u
1
)
r
2
(cos u
2
i sin u
2
) r
1
r
2
[cos(u
1
u
2
) i sin(u
1
u
2
)]
■
r
r
1
2
[cos(u
1
u
2
) i sin(u
1
u
2
)]
■
DeMoivre’s Theorem:
[r(cos u i sin u)]
n
r
n
[cos(nu) i sin(nu)]
■
The distinct nth roots of r(cos u i sin u) are
n
r
cos
u
n
2kp
i sin
u
n
2kp
(k 0, 1, 2, . . . , n 1).
■
The distinct nth roots of unity are
cos
2k
n
p
i sin
2k
n
p
(k 0, 1, 2, . . . , n 1).
■
If P (x
1
, y
1
) and Q (x
2
, y
2
), then PQ
x
2
x
1
, y
2
y
1
.
■
a, b
a
2
b
2
■
If u a, b and k is a scalar, then ku ka, kb.
■
If u a, b and v c, d , then
u v a c, b d and u v a c, b d .
■
Properties of Vector Addition and Scalar Multiplication: For any vectors u, v, and w and any scalars
r and s,
1. u (v w) (u v) w
2. u v v u
3. v 0 v 0 v
4. v (v) 0
5. r(u v) ru rv
6. (r s)v rv sv
7. (rs)v r(sv) s(rv)
8. 1v v
9. 0
v 0 r0
■
If v a, b ai bj, then
a v cos u and b v sin u,
where u is the direction angle of v.
■
If u a, b ai bj and v c, d ci dj, then
u
v ac bd.
■
If u is the angle between nonzero vectors u and v, then
u
v uv cos u.
■
Schwarz Inequality: u
v uv.
■
Vectors u and v are orthogonal exactly when u
v 0.
■
proj
v
u
v
■
comp
v
u u cos u, where u is the angle between u and v.
u
v
v
u
v
v
2
r
1
(cos u
1
i sin u
1
)
r
2
(cos u
2
i sin u
2
)

664 CHAPTER 9 Applications of Trigonometry
1. Simplify: i(4 2i) 3 i.
2. Simplify: 3 2i 1 2i.
3. Graph the equation z 2 in the complex plane.
4. Graph the equation z 3 1 in the complex plane.
5. Express in polar form: 1 3
i.
6. Express in polar form: 4 5i.
In Questions 7–11, multiply or divide, and express the answer
in the form a bi.
7. 2
cos
1
p
2
i sin
1
p
2
4
cos
p
6
i sin
p
6
8. 3
cos
p
8
i sin
p
8
2
cos
3
8
p
i sin
3
8
p
9.
10.
cos
1
p
2
i sin
1
p
2
18
11.
3
3
cos
5
3
p
6
i sin
5
3
p
6
12
In Questions 12–16, solve the given equation in the complex
number system, and express your answers in polar form.
12. x
3
i
13. x
6
1
14. x
8
3
3i
15. x
4
i
16. x
3
1 i
In Questions 17–20, let u 2, 5 and v 6, 1. Find
17. u v
18. 3v
19. 2v 4u
20. 3u
1
2
v
In Questions 21–24, let u 3i j and v 2i 5j. Find
21. 4u v
22. u 2v
23. u v
24. u v
12
cos
7
1
p
2
i sin
7
1
p
2
3
cos
5
1
p
2
i sin
5
1
p
2
25. Find the components of the vector v such that v 5 and
the direction angle of v is 45°.
26. Find the magnitude and direction angle of 3i 4j.
27. Find a unit vector whose direction is opposite the direction
of 3i 6j.
28. An object at the origin is acted upon by a 10-pound force
with direction angle 90° and a 20-pound force with direc-
tion angle 30°. Find the magnitude and direction of the
resultant force.
29. A plane flies in the direction 120° with an air speed of 300
mph. The wind is blowing from north to south at 40 mph.
Find the course and ground speed of the plane.
30. An object weighing 40 pounds lies on an inclined plane
that makes a 30° angle with the horizontal. Find the com-
ponents of the weight parallel and perpendicular to the
plane.
In Questions 31–34, u 4, 3, v 1, 6, and w 5, 0.
Find
31. u
v
32. u
u v
v
33. (u v)
w
34. (u w)
(w 3v)
35. What is the angle between the vectors 5i 2j and
3i j?
36. Is 3i 2j orthogonal to 4i 6j?
In Questions 37 and 38, u 4i 3j and v 2i j. Find
37. proj
v
u
38. comp
u
v
39. If u and v have the same magnitude, show that u v and
u v are orthogonal.
40. If u and v are nonzero vectors, show that the vector u kv
is orthogonal to v, where k .
41. A 3500-pound automobile is on an inclined ramp that
makes a 30° angle with the horizontal. Find the force re-
quired to keep it from rolling down the ramp, assuming
that the only force that must be overcome is that due to
gravity.
42. A sled is pulled along level ground by a rope that makes a
50° angle with the horizontal. If a force of 40 pounds is used
to pull the sled, how much work is done in pulling it 100
feet?
u
v
v
2
REVIEW QUESTIONS

CHAPTER 9 Test 665
Chapter
9
Test
Sections 9.1 and 9.2
Note: If the directions say “show your work,” it is not accept-
able to respond “I used my calculator”.
1. Plot the number
3
2
i
(6 2i) in the complex plane.
2. Calculate the product (3 3i)
6
and express your answer in
the form a bi. Show your work.
3. Find the exact value of 3 2i. Show your work.
4. Find the cube roots (in polar form) of 64
cos
1
p
6
i sin
1
p
6
.
No decimal approximations allowed.
5. Let z 5 3i. Find each of the following and show your
work.
(a) z
2
(b) zz
, where z
is the complex conjugate of z.
6. Find the cube roots (in polar form) of 1 3
i.
7. Sketch the graph of the equation z 3 5 in the complex
plane.
8. Solve: x
4
i. Express your answers in polar form.
9. Compute 3
cos
3
8
p
i sin
3
8
p
13
cos
p
8
i sin
p
8
and
express your answer in the form a bi. Show your work.
10. Solve: x
4
648 648 3
i. Express your answers in
the form a bi.
11. Convert to polar form and divide:
3
1
0i
i
. Express the exact
answer in polar form.
12. Solve: x
3
x
2
x 1 0. [Hint: First, multiply both
sides by x 1.]
Sections 9.3 and 9.4
13. Find a vector with initial point at the origin that is equiva-
lent to PQ
, where P (1, 4) and Q (8, 9).
14. If u 3, 5, v 2, 1 and w 3, 1, find
(u 2v)
(3u w).
15. If u 5
j and v 11
i, find
(a) u v (b) u v (c) 6u 5v
16. Find the angle (in radians) between the vectors 9, 3 and
0, 2. Round your answer to four decimal places.
17. Find the component form of the vector v whose magnitude
is 3 and whose direction angle is 210.
18. Find a real number k such that 3ki 6j is orthogonal to
7i j.
19. Find a unit vector that has the same direction as 7i 6j.
20. Find comp
v
u, where u i 2j and v 3i j.
21. If vectors u
1
, u
2
, u
3
, . . . , u
k
act on an object at the origin,
the resultant force is defined to be u
1
u
2
u
3
. . .
u
k
.
(a) Find the resultant force when u
1
1, 6, u
2
7, 3,
u
3
2, 0, and u
4
9, 8.
(b) Find a vector v such that the resultant force of u
1
, u
2
, u
3
,
u
4
, v is 0.
22. Find the work done by a constant force F 8i j as the
point of application of F moves along the vector PQ
, where
P 1, 3 and Q 5, 3.
23. A river flows from west to east. A swimmer on the north
bank swims at 3.9 mph along a straight course that makes a
75 angle with the north bank of the river. He reaches the
south bank at a point directly south of his starting point.
How fast is the current in the river? Round your answer to
two decimal places.
24. A child pulls a wagon along a level sidewalk by exerting a
force of 17 pounds on the wagon handle, which makes an
angle of 20 with the horizontal. How much work is done in
pulling the wagon 200 feet? Round your answer to two dec-
imal places.
