Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


ROOTS OF UNITY
The n distinct nth roots of 1 (the solutions of z
n
1) are called the nth roots
of unity. Since cos 0 1 and sin 0 0, the polar form of the number 1 is
cos 0 i sin 0. Applying the root formula with r 1 and u 0 shows that
EXAMPLE 5
Find the cube roots of unity.
SOLUTION Apply the formula with n 3 and k 0, 1, 2:
k 0: cos 0 i sin 0 1,
k 1: cos
2
3
p
i sin
2
3
p
1
2
2
3
i,
k 2: cos
4
3
p
i sin
4
3
p
1
2
2
3
i. ■
Denote by v the first complex cube root of unity obtained in Example 5:
v cos
2
3
p
i sin
2
3
p
.
If we use DeMoivre’s Theorem to find v
2
and v
3
, we see that these numbers are
the other two cube roots of unity found in Example 5:
v
2
cos
2
3
p
i sin
2
3
p
2
cos
4
3
p
i sin
4
3
p
,
v
3
cos
2
3
p
i sin
2
3
p
3
cos
6
3
p
i sin
6
3
p
cos 2p i sin 2p
1 0
i 1.
In other words, all the cube roots of unity are powers of v. The same thing is true
in the general case.
636 CHAPTER 9 Applications of Trigonometry
Roots
of Unity
For each positive integer n, there are n distinct nth roots of unity:
cos
2k
n
p
i sin
2k
n
p
(k 0, 1, 2, . . . , n 1).
Roots
of Unity
Let n be a positive integer with n 1. Then the number
z cos
2
n
p
i sin
2
n
p
is an nth root of unity and all the nth roots of unity are
z, z
2
, z
3
, z
4
, . . . z
n1
, z
n
1.
The nth roots of unity have an interesting geometric interpretation. Every nth
root of unity has absolute value 1 by the Pythagorean identity:
cos
2k
n
p
i sin
2k
n
p
cos
2k
n
p
2
sin
2k
n
p
2
cos
2
2k
n
p
sin
2
2k
n
p
1.
Therefore, in the complex plane, every nth root of unity is exactly 1 unit from the
origin. In other words, the nth roots of unity all lie on the unit circle.
EXAMPLE 6
Find the fifth roots of unity.
SOLUTION They are
cos
2k
5
p
i sin
2k
5
p
(k 0, 1, 2, 3, 4),
that is,
cos 0 i sin 0 1, cos
2
5
p
i sin
2
5
p
, cos
4
5
p
i sin
4
5
p
,
cos
6
5
p
i sin
6
5
p
, cos
8
5
p
i sin
8
5
p
.
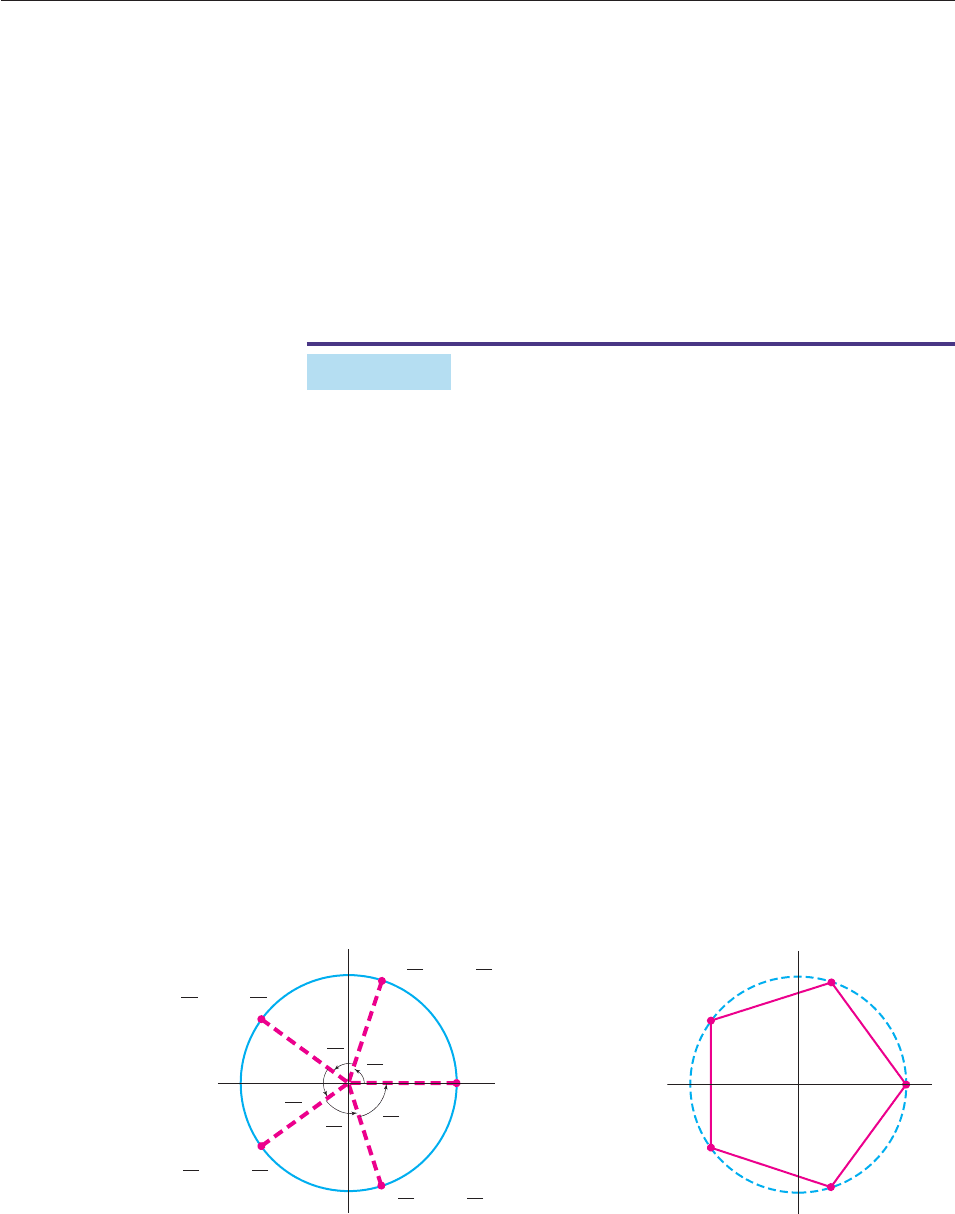
These five roots can be plotted in the complex plane by starting at 1 1 0i and
moving counterclockwise around the unit circle, moving through an angle of
2p/5 at each step, as shown in Figure 9–6. If you connect these five roots, they
form the vertices of a regular pentagon (Figure 9–7). ■
Figure 9–6 Figure 9–7
+ i sincos
2π
5
2π
5
4π
5
4π
5
+ i sin
cos 0 + i sin 0
cos
2π
5
1
1
2π
5
+ i sincos
8π
5
8π
5
+ i sincos
6π
5
6π
5
2π
5
2π
5
2π
5
SECTION 9.2 DeMoivre’s Theorem and nth Roots of Complex Numbers 637
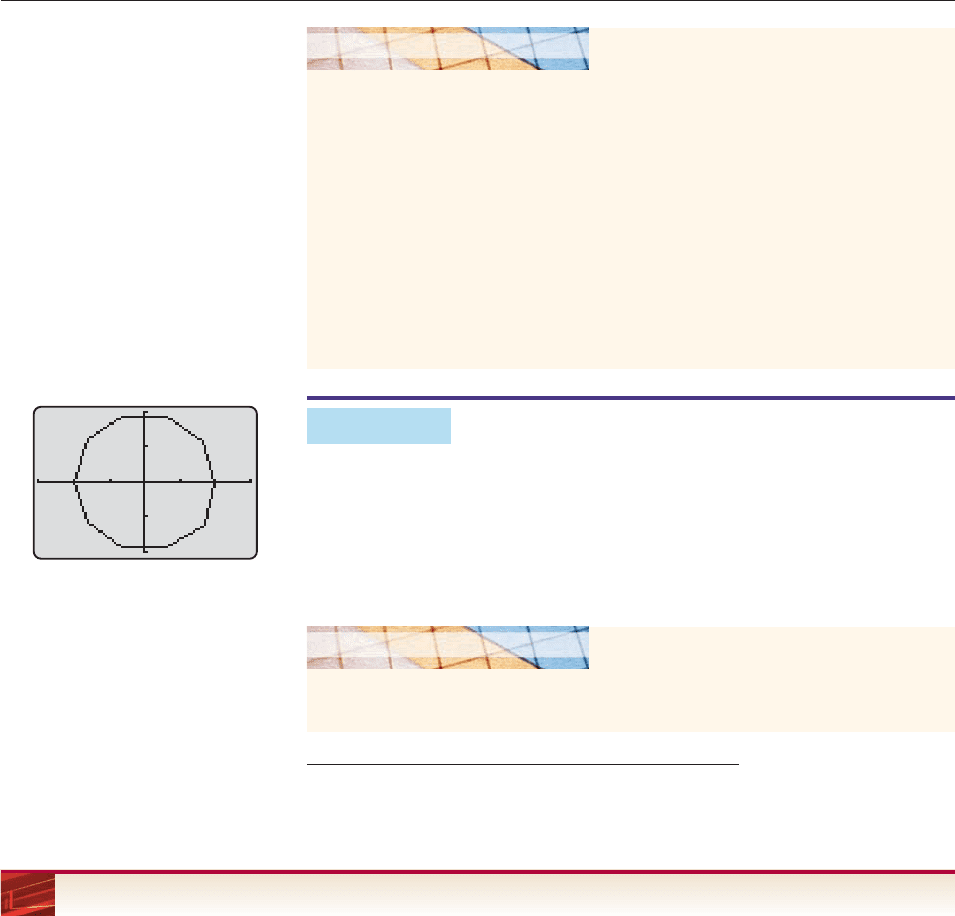
EXAMPLE 7
Find the tenth roots of unity graphically.
SOLUTION Graph the unit circle as in the preceding exploration, but use
2p/10 as the t-step. The result (Figure 9–8) is a regular decagon whose vertices
are the tenth roots of unity. By using the trace feature, you can approximate each
of them.
638 CHAPTER 9 Applications of Trigonometry
With your calculator in parametric graphing mode, set these range values:
0 t 2p, t-step .067,
1.5 x 1.5, 1 y 1
and graph the unit circle, whose parametric equations are
x cos t and y sin t.*
Reset the t-step to be 2p/5 and graph again. Your screen now looks exactly like the
red lines in Figure 9–7 because the calculator plotted only the five points correspon-
ding to t 0, 2p/5, 4p/5, 6p/5, 8p/5
†
and connected them with the shortest pos-
sible segments. Use the trace feature to move along the graph. The cursor will jump
from vertex to vertex, that is, it will move from one fifth root of unity to the next.
GRAPHING EXPLORATION
*On wide-screen calculators, use 2 x 2 or 1.7 x 1.7 so that the unit circle looks like a circle.
†
The point corresponding to t 10p/5 2p is the same as the one corresponding to t 0.
−1
−1.5 1.5
1
Figure 9–8
Verify that the two tenth roots of unity in the first quadrant are (approximately)
.8090 .5878i and .3090 .9511i.
GRAPHING EXPLORATION
EXERCISES 9.2
In Exercises 1–6, calculate the given product and express your
answer in the form a bi.
1.
cos
1
p
2
i sin
1
p
2
6
2.
cos
p
5
i sin
p
5
20
3.
2
cos
2
p
4
i sin
2
p
4
8
4.
2
cos
6
p
0
i sin
6
p
0
10
5.
3
cos
7
3
p
0
i sin
7
3
p
0
5
6.
3
4
cos
7
3
p
6
i sin
7
3
p
6
12
In Exercises 7–14, calculate the product by expressing the
number in polar form and using DeMoivre’s Theorem.
Express your answer in the form a bi.
7.
1
2
2
3
i
3
8.
2
2
2
2
i
4
9. (1 i)
12
10. (2 2i)
8
11.
2
3
1
2
i
10
12.
1
2
2
3
i
20
13.
1
2
i
2
14
14. (1 3
i)
8
In Exercises 15 and 16, find the indicated roots of unity and
express your answers in the form a bi.
15. Fourth roots of unity 16. Sixth roots of unity
In Exercises 17–30, find the nth roots in polar form.
17. 36
cos
p
3
i sin
p
3
; n 2
18. 64
cos
p
4
i sin
p
4
; n 2
■

19. 64
cos
p
5
i sin
p
5
; n 3
20. 8
cos
1
p
0
i sin
1
p
0
; n 3
21. 81
cos
1
p
2
i sin
1
p
2
; n 4
22. 16
cos
p
7
i sin
p
7
; n 5
23. 1; n 5 24. 1; n 7
25. i; n 5 26. i; n 6
27. 1 i; n 2 28. 1 3
i; n 3
29. 83
8i; n 4
30. 162
162
i; n 5
In Exercises 31–40, solve the given equation in the complex
number system.
31. x
6
1 32. x
6
64 0
33. x
3
i 34. x
4
i
35. x
3
27i 0 36. x
6
729 0
37. x
5
243i 0 38. x
7
1 i
39. x
4
1 3
i 40. x
4
8 83
i
In Exercises 41–46, represent the roots of unity graphically.
Then use the trace feature to obtain approximations of the form
a bi for each root (round to four places).
41. Seventh roots of unity 42. Fifth roots of unity
43. Eighth roots of unity 44. Twelfth roots of unity
45. Ninth roots of unity 46. Tenth roots of unity
SECTION 9.3 Vectors in the Plane 639
47. Solve the equation x
3
x
2
x 1 0. [Hint: First find the
quotient when x
4
1 is divided by x 1 and then consider
solutions of x
4
1 0.]
48. Solve the equation x
4
x
3
x
2
x 1 0. [Hint: Con-
sider x
5
1 and x 1 and see Exercise 47.]
49. Solve x
5
x
4
x
3
x
2
x 1 0. [Hint: Consider
x
6
1 and x 1 and see Exercise 47.]
50. What do you think are the solutions of
x
n1
x
n2
x
3
x
2
x 1 0? (See Exer-
cises 47–49.)
THINKERS
51. In the complex plane, identify each point with its complex
number label. The unit circle consists of all points (num-
bers) z such that z 1. Suppose v and w are two points
(numbers) that move around the unit circle in such a way
that v w
12
at all times. When w has made one complete
trip around the circle, how many trips has v made? [Hint:
Think polar and DeMoivre.]
52. Suppose u is an nth root of unity. Show that 1/u is also an
nth root of unity. [Hint: Use the definition, not polar form.]
53. Let u
1
, u
2
, . . . , u
n
be the distinct nth roots of unity and sup-
pose v is a nonzero solution of the equation
z
n
r(cos u i sin u).
Show that vu
1
, vu
2
, . . . , vu
n
are n distinct solutions of the
equation. [Remember: Each u
i
is a solution of x
n
1.]
54. Use the formula for nth roots and the identities
cos(x p) cos x sin(x p) sin x
to show that the nonzero complex number r(cos u i sin u)
has two square roots and that these square roots are nega-
tives of each other.
9.3 Vectors in the Plane
■ Find the components and magnitude of a vector.
■ Use scalar multiplication, vector addition, and vector
subtraction.
■ Find a unit vector with the same direction as a given
vector, v.
■ Find the direction angle of a vector.
■ Use vectors to solve applied problems.
Once a unit of measure has been agreed upon, quantities such as area, length,
time, and temperature can be described by a single number. Other quantities, such
as an east wind of 10 mph, require two numbers to describe them because they
Section Objectives

involve both magnitude and direction. Such quantities are called vectors and are
represented geometrically by a directed line segment or arrow, as in Figure 9–9.
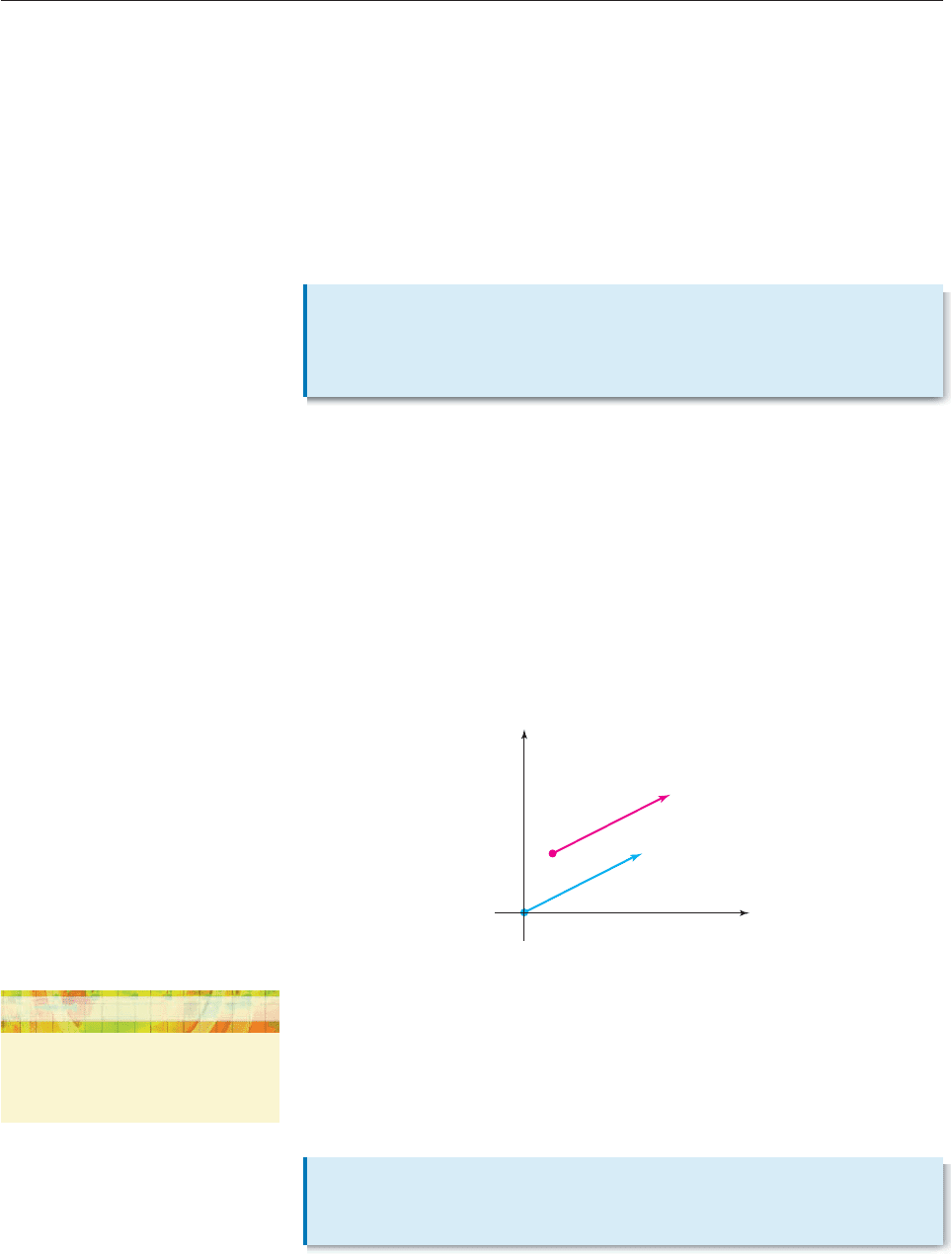
Figure 9–9
When a vector extends from a point P to a point Q, as in Figure 9–9(a), P is
called the initial point of the vector and Q is called the terminal point, and the
vector is written PQ
. Its length is denoted by PQ
. When the endpoints are not
specified, as in Figure 9–9(b), vectors are denoted by boldface letters such as u,
v, and w. The length of a vector u is denoted by u and is called the magnitude
of u.
If u and v are vectors with the same magnitude and direction, we say that u
and v are equivalent and write u v. Some examples are shown in Figure 9–10.
Figure 9–10
EXAMPLE 1
Let P (1, 2), Q (5, 4), O (0, 0), and R (4, 2), as in Figure 9–11. Show
that PQ
OR
.
SOLUTION The distance formula shows that PQ
and OR
have the same length:
PQ
(5 1
)
2
(4
2)
2
4
2
2
2
20.
OR
(4 0
)
2
(2
0)
2
4
2
2
2
20.
v
v
v
u
u
u
u
v
u = v
u ≠ vu ≠ vu ≠ v
same magnitude,
but different
directions
same direction,
but different
magnitudes
different directions,
and different
magnitudes
Q
v
w
u
P
(a) (b)
640 CHAPTER 9 Applications of Trigonometry
3
2
1
5
4
(1, 2)
(5, 4)
12345
O
P
Q
(4, 2)
R
x
y
Figure 9–11
Furthermore, the lines through PQ and OR have the same slope:
slope PQ
4
5
2
1
2
4
1
2
, slope OR
2
4
0
0
2
4
1
2
.
Since PQ
and OR
both point to the upper right on lines of the same slope, PQ
and
OR
have the same direction. Therefore, PQ
OR
. ■
According to the definition of equivalence, a vector may be moved from one
location to another, provided that its magnitude and direction are not changed.
Consequently, we have the following.
SECTION 9.3 Vectors in the Plane 641
Equivalent
Vectors
Every vector PQ
is equivalent to a vector OR
with initial point at the origin:
If P (x
1
, y
1
) and Q (x
2
, y
2
), then
PQ
OR
, where R (x
2
x
1
, y
2
y
1
).
Proof The proof is similar to the one used in Example 1. It follows from the
fact that PQ
and OR
have the same length,
OR
[(x
2
x
1
)
0]
2
[(y
2
y
1
)
0]
2
(x
2
x
1
)
2
(y
2
y
1
)
2
PQ
,
and that either the line segments PQ and OR are both vertical or they have the
same slope,
slope OR
(
(x
y
2
2
x
y
1
1
)
)
0
0
y
x
2
2
y
x
1
1
slope PQ,
as shown in Figure 9–12. ■
Figure 9–12
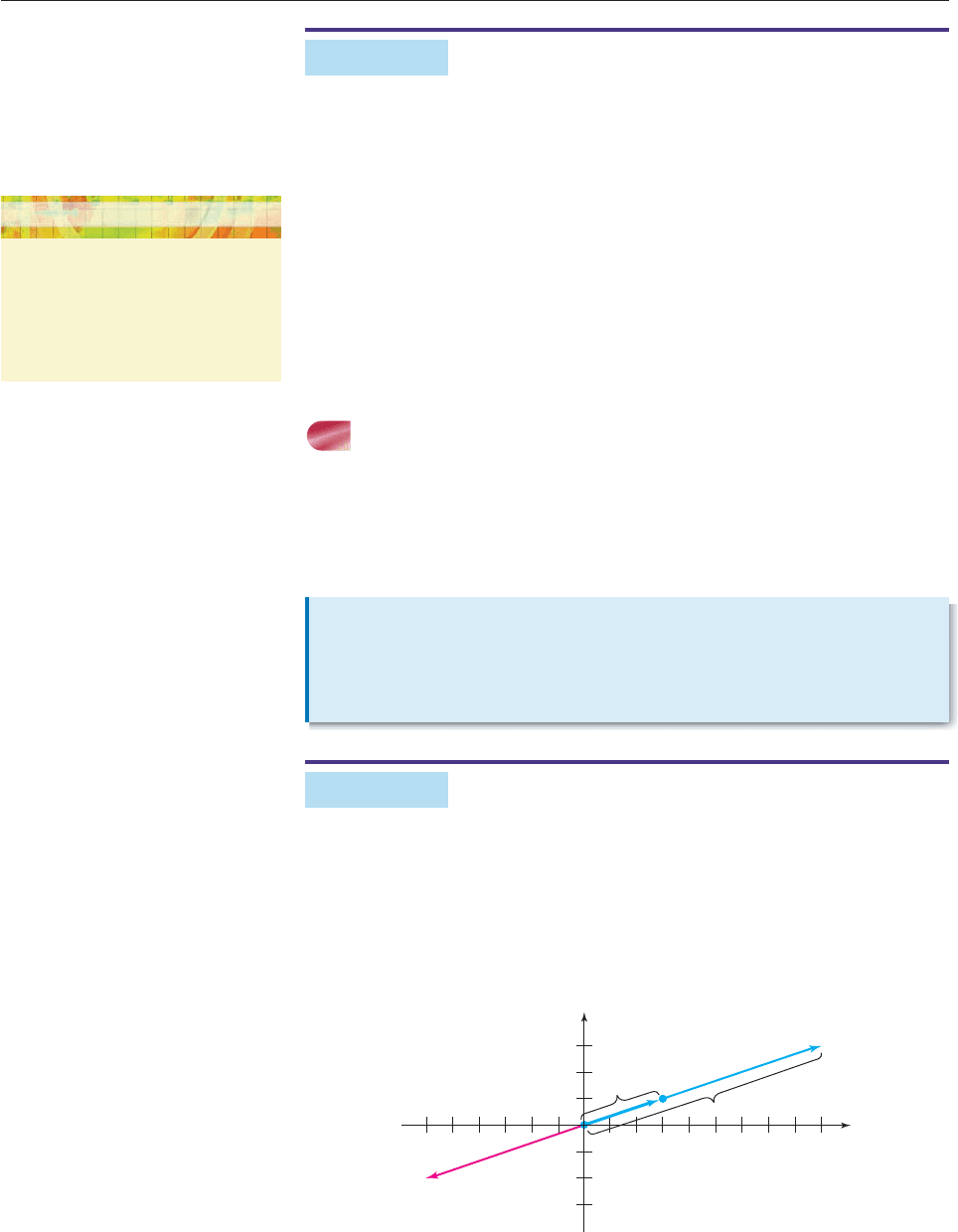
The magnitude and direction of a vector with the origin as initial point are
completely determined by the coordinates of its terminal point. Consequently,
we denote the vector with initial point (0, 0) and terminal point (a, b) by a, b.
The numbers a and b are called the components of the vector a, b.
Since the length of the vector a, b is the distance from (0, 0) to (a, b), the
distance formula shows that
(x
1
, y
1
)
(x
2
, y
2
)
(x
2
– x
1
, y
2
– y
1
)
O
P
Q
R
x
y
Magnitude
The magnitude (or norm) of the vector v a, b is
v
a
2
b
2
.
TECHNOLOGY TIP
Vectors in component form can be
entered on TI-86/89 and HP-39gs by
using [a, b] in place of a, b.
EXAMPLE 2
Find the components and the magnitude of the vector with initial point P (2, 6)
and terminal point Q (4, 3).
SOLUTION According to the fact in the first box on page 641 (with x
1
2,
y
1
6, x
2
4, y
2
3):
PQ
OR
, where R (4 (2), 3 6) (6, 9)
that is,
PQ
OR
6, 9.
Therefore,
PQ
OR
6
2
(
9)
2
36 8
1
117
. ■
VECTOR ARITHMETIC
When dealing with vectors, it is customary to refer to ordinary real numbers
as scalars. Scalar multiplication is an operation in which a scalar k is “multi-
plied” by a vector v to produce another vector denoted by kv. Here is the formal
definition.
642 CHAPTER 9 Applications of Trigonometry
EXAMPLE 3
If v 3, 1, then
3v 33, 1 3
3, 3
1 9, 3,
2v 23, 1 2
3, 2
1 6, 2,
as shown in Figure 9–13:
Figure 9–13
〈3, 1〉
〈−6, −2〉
−2v
3v
v
〈9, 3〉
x
y
TECHNOLOGY TIP
To find the magnitude of a vector, use
NORM in this menu/submenu:
TI-86: VECTOR/MATH
TI-89: MATH/MATRIX/NORMS
Scalar
Multiplication
If k is a real number and v a, b is a vector, then
kv is the vector ka, kb.
The vector kv is called a scalar multiple of v.
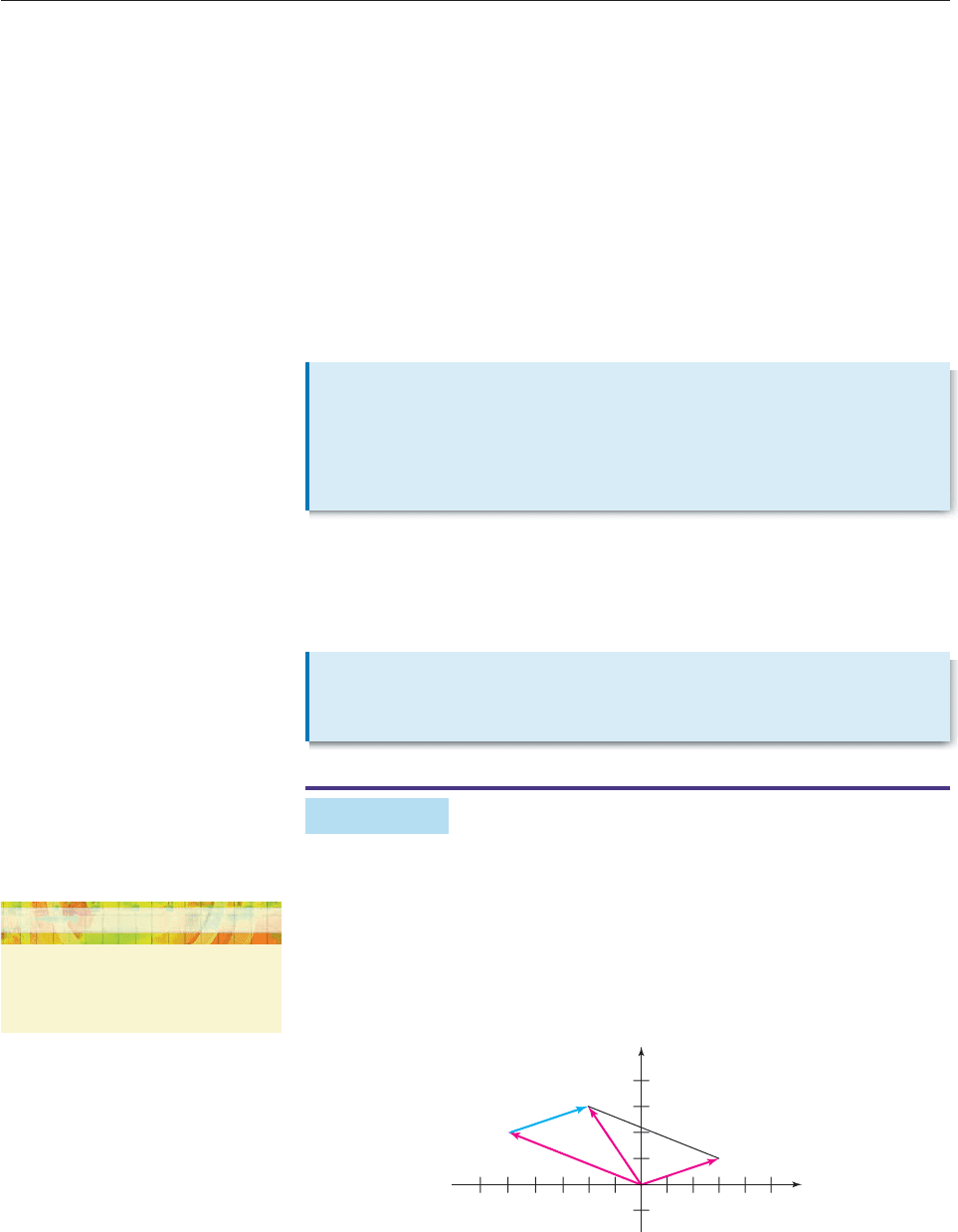
Figure 9–13 shows that 3v has the same direction as v, while 2v has the oppo-
site direction. Also note that
v 3, 1
3
2
1
2
10
2v 6, 2
(6)
2
(2
)
2
40 210.
Therefore,
2v 210 2v 2
v.
Similarly, you can verify that 3v 3
v 3v. ■
Example 3 is an illustration of the following facts.
See Exercise 77 for a proof of this statement.
Vector addition is an operation in which two vectors u and v are added to
produce a new vector denoted u v. Formally, we have the following.
EXAMPLE 4
If u 5, 2 and v 3, 1, find u v.
SOLUTION
u v 5, 2 3, 1 5 3, 2 1 2, 3
as shown in Figure 9–14. ■
Figure 9–14
2
1
3
4
–1–2–5 1 3
x
y
〈3, 1〉
〈−2, 3〉
〈−5, 2〉
u + v
v
v
u
SECTION 9.3 Vectors in the Plane 643
Geometric Interpretation
of Scalar Multiplication
The magnitude of the vector kv is k times the length of v, that is,
kv k
v.
The direction of kv is the same as that of v when k is positive and opposite
that of v when k is negative.
Vector
Addition
If u a, b and v c, d , then
u v a c, b d.
TECHNOLOGY TIP
Vector arithmetic and other vector
operations can be done on TI-86/89
and HP-39gs.

Example 4 is an illustration of these facts.
See Exercise 78 for a proof of these statements.
The negative of a vector v c, d is defined to be the vector (1)v
(1)c, d c, d and is denoted v. Vector subtraction is then defined
as follows.
A geometric interpretation of vector subtraction is given in Exercise 79.
EXAMPLE 5
If u 2, 5 and v 6, 1, find u v.
SOLUTION
u v 2, 5 6, 1 2 6, 5 1 4, 4,
as shown in Figure 9–15. ■
Figure 9–15
The vector 0, 0 is called the zero vector and is denoted 0.
u
u
1
−11
v
x
y
〈2, 5〉
〈6, 1〉
〈−4, 4〉
u − v
−v
644 CHAPTER 9 Applications of Trigonometry
Geometric Interpretations
of Vector Addition
1. If u and v are vectors with the same initial point P, then u v is the
vector PQ
, where PQ
is the diagonal of the parallelogram with adjacent
sides u and v.
2. If the vector v is moved (without changing its magnitude or direction)
so that its initial point lies on the endpoint of the vector u, then u v is
the vector with the same initial point P as u and the same terminal point
Q as v.
Vector
Subtraction
If u a, b and v c, d, then u v is the vector
u (v) a, b c, d
a c, b d.

EXAMPLE 6
If u 1, 6, v 2/3, 4, and w 2, 5/2, find 2u 3v and 4w 2u.
SOLUTION
2u 3v 21, 6 3
2
3
, 4
2, 12 2, 12
0, 0 0,
and
4w 2u 4
2,
5
2
21, 6
8, 10 2, 12
8 (2), 10 12 10, 2. ■
Operations on vectors share many of the same properties as arithmetical
operations on numbers.
Proof If u a, b and v c, d, then because addition of real numbers is
commutative, we have
u v a, b c, d a c, b d
c a, d b c, d a, b v u.
The other properties are proved similarly; see Exercises 53–58. ■
UNIT VECTORS
A vector with length 1 is called a unit vector. For instance, 3/5, 4/5 is a unit
vector, since
3
5
,
4
5
3
5
2
4
5
2
2
9
5
1
2
6
5
2
2
5
5
1.
SECTION 9.3 Vectors in the Plane 645
Properties of Vector
Addition and Scalar
Multiplication
For any vectors u, v, and w and any scalars r and s,
1. u (v w) (u v) w
2. u v v u
3. v 0 v 0 v
4. v (v) 0
5. r(u v) ru rv
6. (r s)v rv sv
7. (rs)v r(sv) s(r v)
8. 1v v
9. 0v 0 and r 0 0
