Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


Arthur S. Aubry/Getty Images
666
DISCOVERY PROJECT 9 Surveying
You might ask, how far apart are two points A and B? Under ordinary circum-
stances, the easiest thing to do would be to measure the distance. However, some-
times it is impractical to make such a direct measurement because of intervening
obstacles. Two historical methods for measuring the distance between the two
mutually invisible points A and B are given below.
1. Find the distance from A to B, using the classic surveyor’s method shown
in the figure below. A transit is used to measure the angle between two
distant objects*, and a reasonably short baseline is measured. Angles are
reported in degrees. Triangles are drawn, and the law of sines (page 606)
is used to calculate the length of unknown edges. To find the distance
from A to B, draw an additional triangle that has AB as one of the sides.
Caution: The picture is not drawn to scale.
(a)
53°
23°
65°
36°
70°
40°
31°
34°
61°
104°
132 ft 5 in
B
A
*A transit is a small telescope on a tripod that can be used to measure angles precisely. (See the
photograph at the left.)
667
2. Find the distance from A to B, using a modern laser range finder. Laser
technology removes the necessity of drawing triangles; the tool provides
a vector (angle and distance) from point to point, so the distance from A
to B can be found by using vector arithmetic in place of repeated applica-
tion of the law of sines. Angles are taken from the internal compass and
are reported in degrees measured clockwise from North (0°), so you have
to convert compass direction angles to angles in standard position. For
example, the angle from point A (straight South) is reported as 180°, but
in standard position, you would list the angle as 270°.
(b)
B
A
132 ft 5 in
298 ft 5 in
127°
173 ft 8 in
85°
180°
288 ft 7 in
42°
This page intentionally left blank

ANALYTIC GEOMETRY
Calling all ships!
T
he planets travel in elliptical orbits around the sun,
and satellites travel in elliptical orbits around the
earth. Parabolic reflectors are used in spotlights, radar
antennas, and satellite dishes. The long-range
navigation system (LORAN) uses hyperbolas to enable
a ship to determine its exact location. See Exercise 54
on page 699.
669
Chapter
© Digital Vision/Getty Images
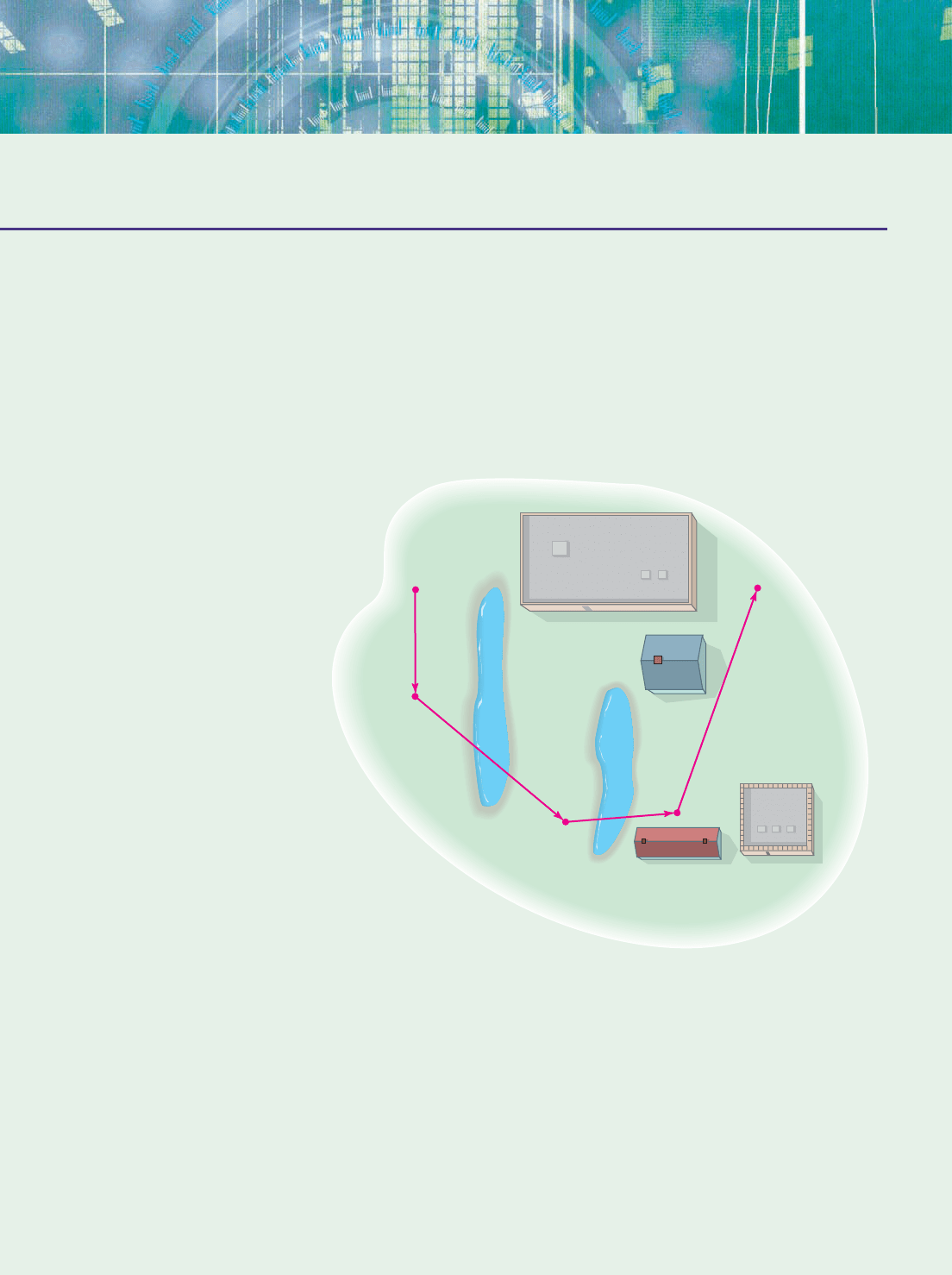
S
Q
P
R
−900
−500 500
900
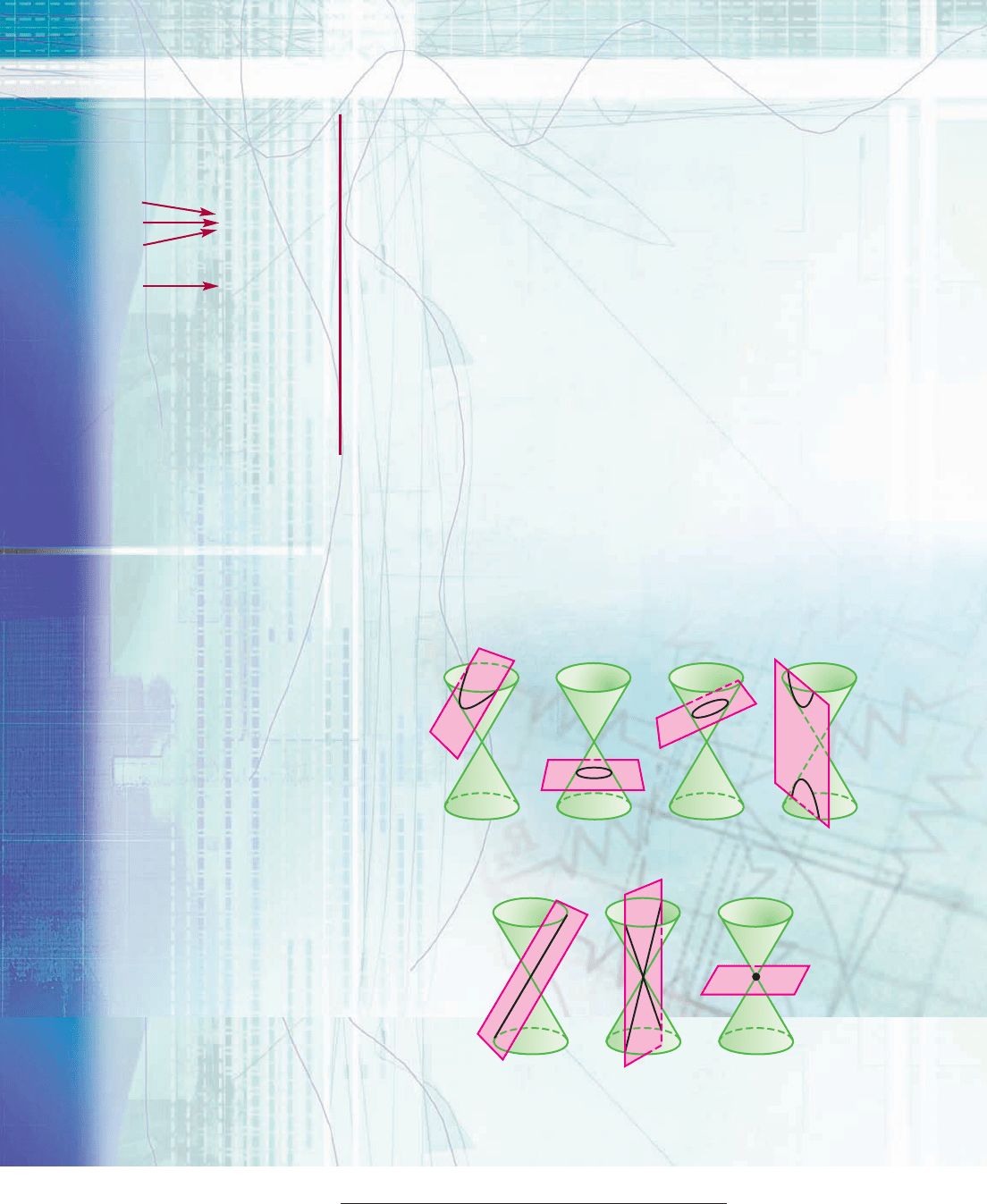
670
670
Chapter Outline
Interdependence of
Sections
10.1 Circles and Ellipses
10.2 Hyperbolas
10.3 Parabolas
10.3.A Special Topics: Parametric Equations for Conic Sections
10.4 Rotations and Second-Degree Equations
10.4.A Special Topics: Rotation of Axes
10.5 Plane Curves and Parametric Equations
10.6 Polar Coordinates
10.7 Polar Equations of Conics
When a right circular cone is cut by a plane, the intersection is a curve
called a conic section, as shown in Figure 10–1. Conic sections were
first studied by the ancient Greeks and over the centuries have ap-
peared time and again in astronomy, warfare, medicine, economics,
and other branches of science. For instance, planets travel in elliptical
orbits, thrown objects trace out parabolas, and certain atomic particles
follow hyperbolic paths.
10.1
10.2 10.4
10.3
10.5
10.6 10.7
*A point, a line, or two intersecting lines are sometimes called degenerate conic sections.
Parabola Circle Ellipse Hyperbola
Line* Two intersecting lines* Point*
P
Figure 10–1
The five sections on the left above
are independent of one another
and may be read in any order. (A
few exercises in Sections 10.2
and 10.3 depend on preceding
sections.)
The only prerequisites for Sections
10.1–10.4 are Sections 1.3 and 2.1.
Basic trigonometry is an additional
prerequisite for Special Topics
10.3.A and 10.4.A, and Sections
10.5–10.7.

SECTION 10.1 Circles and Ellipses 671
10.1 Circles and Ellipses
■ Find the center and radius of a circle from its equation.
■ Use the standard equation of an ellipse to sketch its graph.
■ Set up and solve applied problems involving ellipses.
Let P be a point in the plane, and let r be a positive number. Then the circle with
center P and radius r consists of all points X in the plane such that
Distance from X to P r,
as shown in Figure 10–2. In Section 1.3, we proved the following result.
Section Objectives
Although the Greeks studied conic sections from a purely geometric
point of view, the modern approach is to describe them in terms of the
coordinate plane and distance or as the graphs of certain types of equa-
tions. This was done for circles in Section 1.3 and will be done in Sections
10.1–10.3 for ellipses, hyperbolas, and parabolas.
Sections 10.5–10.7 present a more thorough treatment of parametric
graphing and an alternate method of coordinatizing the plane and graphing.
r
X
P
Figure 10–2
Equation of
a Circle
The circle with center (0, 0) and radius r is the graph of the equation
x
2
y
2
r
2
.
The circle with center (h, k) and radius r is the graph of
(x h)
2
( y k)
2
r
2
.
EXAMPLE 1
Find the center and radius of the circle whose equation is given.
(a) (x 2)
2
(y 7)
2
25
(b) (x 4)
2
(y 3)
2
36
(c) 2x
2
2y
2
4x 12y 12 0
SOLUTION
(a) The right side of the equation is 5
2
. So the center is at (2, 7), and the radius
is 5.

(b) First, we rewrite the equation to match the form in the box above:
(x 4)
2
(y 3)
2
36
(x 4)
2
[y (3)]
2
6
2
.
Hence, the circle has center (4, 3) and radius 6.
(c) We begin by rewriting the equation.
2x
2
2y
2
4x 12y 12 0
Divide both sides by 2: x
2
y
2
2x 6y 6 0
Rearrange terms: (x
2
2x) (y
2
6y) 6
Now we complete the square in both expressions in parentheses by adding 1
to the x-expression and 9 to the y-expression, and adding the same amounts
to the right side of the equation.
(x
2
2x 1) (y
2
6y 9) 6 1 9
Factor: (x 1)
2
(y 3)
2
4
(x 1)
2
(y 3)
2
2
2
The circle has center (1, 3) and radius 2. ■
The preceding discussion of circles provides the model for our discussion of the
other conic sections. In each case, the conic is defined in terms of points and dis-
tances, and its Cartesian equation is determined. The standard form of the equation
of a conic includes the key information necessary for a rough sketch of its graph,
just as the standard form of the equation of a circle tells you its center and radius.
ELLIPSES
Definition. Let P and Q be points in the plane, and let r be a number greater
than the distance from P to Q. The ellipse with foci* P and Q is the set of all
points X such that
(Distance from X to P) (Distance from X to Q) r.
To draw this ellipse, take a piece of string of length r and pin its ends on P and Q.
Put your pencil point against the string and move it, keeping the string taut. You
will trace out the ellipse, as shown in Figure 10–3.
672 CHAPTER 10 Analytic Geometry
*“Foci” is the plural of “focus.”
P Q
Figure 10–3

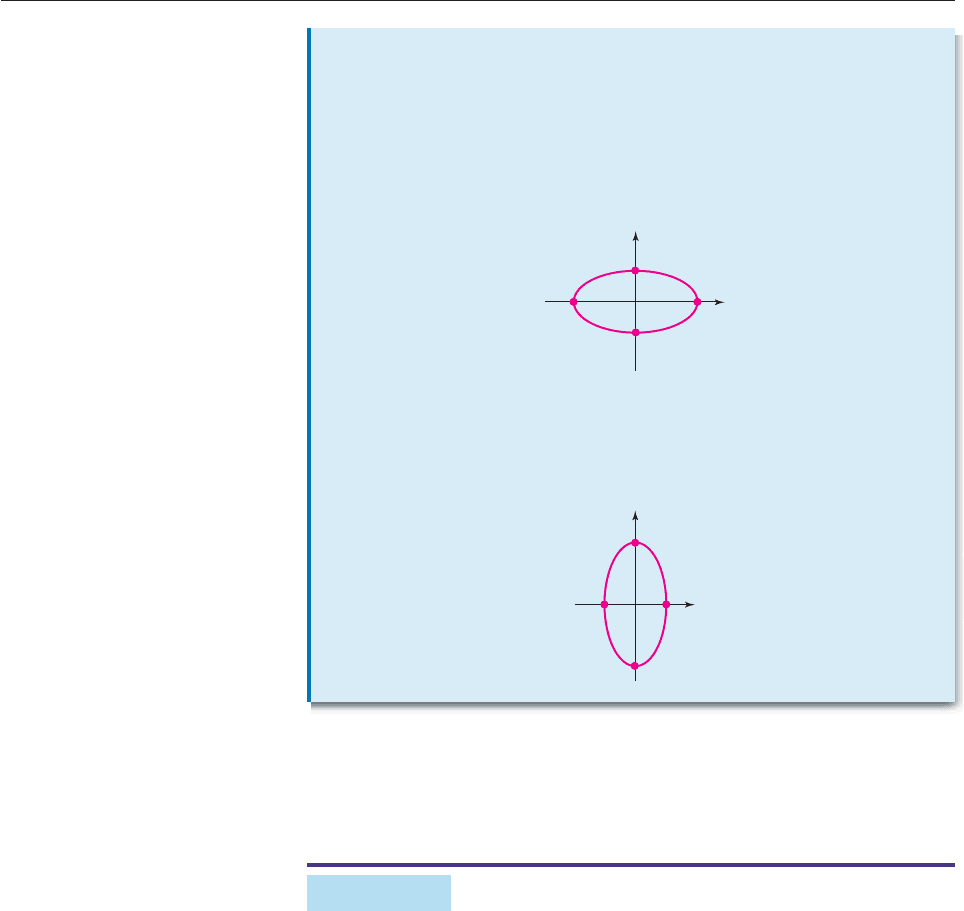
The midpoint of the line segment from P to Q is the center of the ellipse. The
points where the straight line through the foci intersects the ellipse are its vertices.
The major axis of the ellipse is the line segment joining the vertices; its minor
axis is the line segment through the center, perpendicular to the major axis, as
shown in Figure 10–4.
Equation. Suppose that the foci P and Q are on the x-axis, with coordinates
P (c, 0) and Q (c, 0) for some c 0.
Let a r/2, so that 2a r. Then the point (x, y) is on the ellipse exactly when
[Distance from (x, y) to P] [Distance from (x, y) to Q] r
(x c
)
2
(
y 0)
2
(x c
)
2
(
y 0)
2
2a
(x c
)
2
y
2
2a
(x c
)
2
y
2
.
Squaring both sides and simplifying (Exercise 76), we obtain
a
(x c
)
2
y
2
a
2
cx.
Again squaring both sides and simplifying, we have
(a
2
c
2
)x
2
a
2
y
2
a
2
(a
2
c
2
).
To simplify the form of this equation, let b
a
2
c
2
*
so that b
2
a
2
c
2
and
the equation becomes
b
2
x
2
a
2
y
2
a
2
b
2
.
Dividing both sides by a
2
b
2
shows that the coordinates of every point on the
ellipse satisfy the equation
x
a
2
2
y
b
2
2
1.
Conversely, it can be shown that every point whose coordinates satisfy this equa-
tion is on the ellipse. When the equation is in this form the x- and y-intercepts of the
graph are easily found. For instance, to find the x-intercepts, we set y 0 and solve
x
a
2
2
0
b
2
2
1
x
2
a
2
x a.
Similarly, we find the y-intercepts by setting x 0 and solving for y:
0
a
2
2
b
y
2
2
1
y
2
b
2
y b.
An analogous argument applies when the foci are on the y-axis and leads to
this conclusion.
SECTION 10.1 Circles and Ellipses 673
P
Vertex
Vertex
Center
Foci
Minor
axis
Major
axis
Q
Figure 10–4
*The distance between the foci is 2c. Since r 2a and r 2c by definition, we have 2a 2c, and
hence, a c. Therefore, a
2
c
2
is a positive number and has a real square root.
In the preceding box a b, but don’t let all the letters confuse you: When
the equation is in standard form, the denominator of the x term tells you the
x-intercepts, the denominator of the y term tells you the y-intercepts, and the
major axis is the longer one, as illustrated in the following examples.
EXAMPLE 2
Identify the intercepts, axes, vertices and foci of the ellipse
x
9
2
2
y
5
2
1
and sketch its graph.
SOLUTION The equation can be written as
3
x
2
2
5
y
2
2
1.
Its x-intercepts are 3 and its y-intercepts are 5. Since the larger denominator
5
2
is in the y-term of the equation, the major axis lies on the y-axis. So the vertices
are determined by the y-intercepts: (0, 5) and (0, 5). The foci have coordinates
(0, c) and (0, c), where c is the square root of the difference of the larger and
smaller denominators:
c
5
2
3
2
16 4.
674 CHAPTER 10 Analytic Geometry
Standard Equations
of Ellipses Centered
at the Origin
y
−a
−b
a
b
x
y
−b
−a
b
a
x
Let a and b be real numbers with a b 0. Then the graph of each of the
following equations is an ellipse centered at the origin:
x-intercepts: ay-intercepts: b
x
a
2
2
y
b
2
2
1
major axis on the x-axis, with vertices (a, 0) and (a, 0)
foci: (c, 0) and (c, 0), where c
a
2
b
2
x-intercepts: by-intercepts: a
x
b
2
2
y
a
2
2
1
major axis on the y-axis, with vertices (0, a) and (0, a)
foci: (0, c) and (0, c), where c
a
2
b
2
Thus, the foci are (0, 4) and (0, 4). The minor axis (the shorter one, correspon-
ding to the smaller denominator in the equation) lies on the x-axis.
By plotting the four intercepts and a few more points, we obtain the graph of
the ellipse in Figure 10–5. ■
EXAMPLE 3
Identify and sketch the graph of the equation 4x
2
9y
2
36.
SOLUTION To identify the graph, we put the equation in standard form.
4x
2
9y
2
36
Divide both sides by 36:
4
3
x
6
2
9
3
y
6
2
3
3
6
6
Simplify:
x
9
2
y
4
2
1
x
3
2
2
y
2
2
2
1.
This form of the equation shows that the graph is an ellipse with
x-intercepts: 3 and y-intercepts: 2.
The major axis is the x-axis (because the larger denominator 3
2
is in the x-term).
The foci are on the major axis, so they have the form (c, 0) and (c, 0), where
c 3
2
2
2
5
.
A hand-sketched graph is shown in Figure 10–6. To graph this ellipse on a calcu-
lator, we first solve its equation for y:
4x
2
9y
2
36
Subtract 4x
2
from both sides: 9y
2
36 4x
2
Divide both sides by 9: y
2
36
9
4x
2
.
Taking square roots on both sides, we see that
y
36
9
4
x
2
or y
36
9
4
x
2
.
Graphing both of these equations on the same screen, we obtain Figure 10–7. ■
Figure 10–6 Figure 10–7
−3.1
4.7
3.1
−4.7
–1–2–3
–1
1
+= 1
x
2
9
2
–2
213
x
y
y
2
4
SECTION 10.1 Circles and Ellipses 675
2
2
2
4
4
6
6
424
x
y
Figure 10–5
TECHNOLOGY TIP
On most calculators, you can graph
both equations in Example 3 simulta-
neously by keying in
y {1, 1}
36
9
4
x
2
.
