Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


626
626
Chapter Outline
Interdependence of
Sections
9.1 The Complex Plane and Polar Form for Complex Numbers
9.2 DeMoivre’s Theorem and nth Roots of Complex Numbers
9.3 Vectors in the Plane
9.4 The Dot Product
Trigonometry has a variety of useful applications in geometry, algebra,
and the physical sciences, several of which are discussed in this chapter.
9.1 The Complex Plane and Polar Form for Complex Numbers*
■ Explore the complex plane.
■ Convert a complex number from rectangular to polar form.
■ Multiply and divide complex numbers in polar form.
The complex number system can be represented geometrically by the coordinate
plane:
The complex number a bi corresponds to the point (a, b) in the plane.
For example, the point (2, 3) in Figure 9–1 is labeled by 2 3i, and similarly for
the other points shown:
Figure 9–1
When the coordinate plane is labeled by complex numbers in this way, it is called
the complex plane. Each real number a a 0i corresponds to the point (a, 0)
on the horizontal axis; so this axis is called the real axis. The vertical axis is called
the imaginary axis because every imaginary number bi 0 bi corresponds to
the point (0, b) on the vertical axis.
The absolute value of a real number c is the distance from c to 0 on the
number line (see page 12). So we define the absolute value (or modulus) of the
2 + 3i
4 − 3i
2i = 0 + 2i
5.5 = 5.5 + 0i
−6 + 2.3i
−5 − 3i
Section Objectives
9.1 9.2
9.3 9.4
*Section 4.7 is a prerequisite for this section.
TECHNOLOGY TIP
To do complex arithmetic on TI-86 and
HP-39gs, enter a bi as (a, b). On
other calculators, use the special i key
whose location is:
TI-84/89: keyboard
Casio 9850: OPTN/CPLX
Sections 9.1 and 9.3 are independent
of each other and may be read in
either order.
complex number a bi to be the distance from a bi to the origin in the com-
plex plane:
a bi distance from (a, b) to (0, 0)
(a 0
)
2
(b
0)
2
.
Therefore, we have the following.
EXAMPLE 1
Find the modulus of each of the following complex numbers:
(a) 3 2i (b) 4 5i (c) 3i
SOLUTION
(a) 3 2i
3
2
2
2
13.
(b) 4 5i
4
2
(
5)
2
41.
(c) 3i 0 3i, so
3i 0 3i 0
2
(
3)
2
9
3. ■
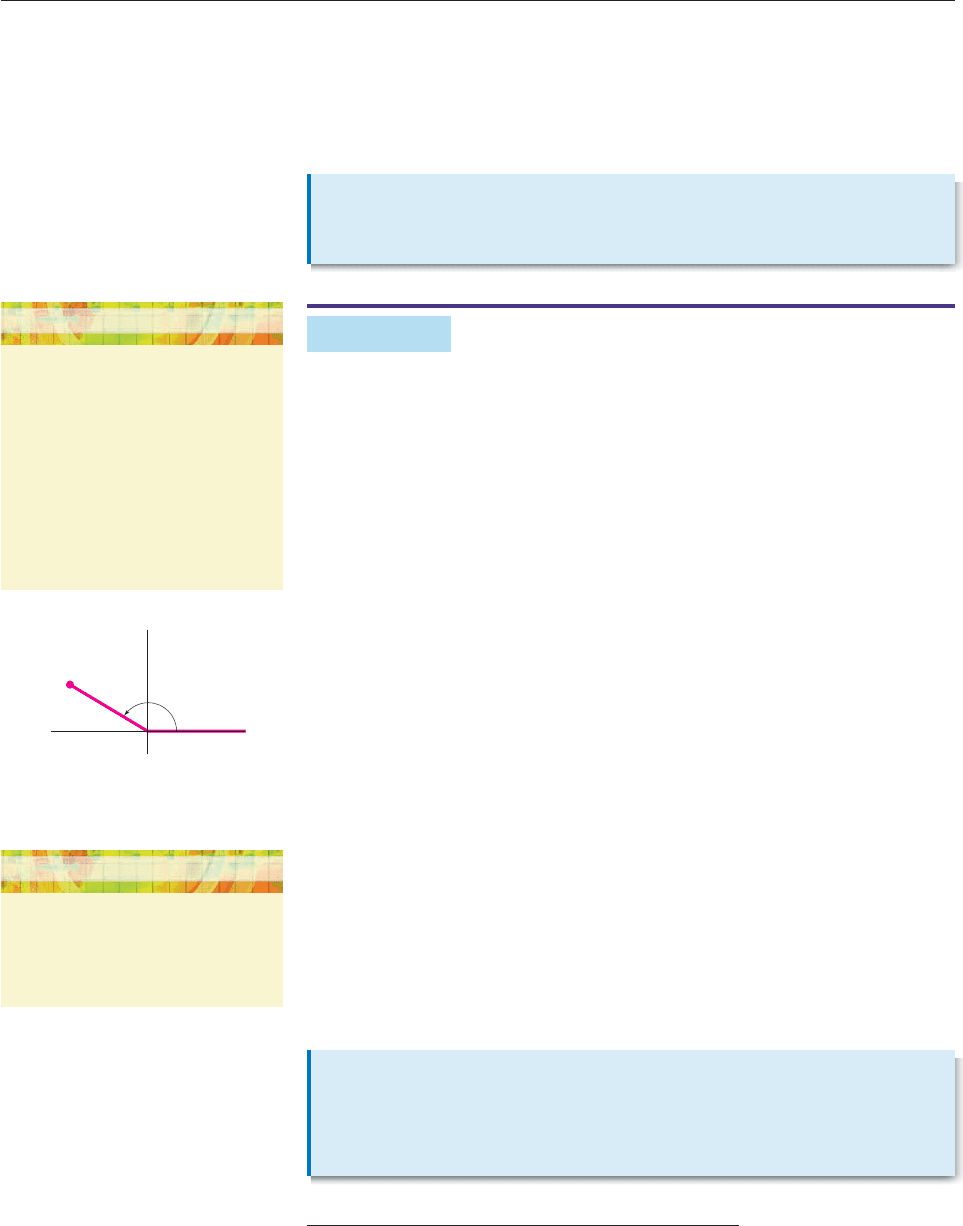
Let a bi be a nonzero complex number, and denote a bi by r. Then r is
the length of the line segment joining (a, b) and (0, 0) in the plane. Let u be the
angle in standard position with this line segment as its terminal side (Figure 9–2).
According to the point-in-the-plane description of sine and cosine,
cos u
a
r
and sin u
b
r
,
so
a r cos u and b r sin u.
Consequently,
a bi r cos u (r sin u)i r (cos u i sin u).*
When a complex number a bi is written in this way, it is said to be in polar
form or trigonometric form. The angle u is called the argument and is usually
expressed in radian measure. The number 0 can also be written in polar notation
by letting r 0 and u be any angle. Thus, we have the following.
SECTION 9.1 The Complex Plane and Polar Form for Complex Numbers 627
Absolute
Value
The absolute value (or modulus) of the complex number a bi is
a bi
a
2
b
2
.
*It is customary to place i in front of sin u rather than after it. Some books abbreviate r(cos u i sin u)
as r cis u.
TECHNOLOGY TIP
To find the absolute value of a complex
number, use the ABS key, which is in
this menu/submenu:
TI-84: MATH/CPX
TI-86: CPLX
TI-89: MATH/COMPLEX
Casio: OPTN/CPLX
HP-39gs: Keyboard
TECHNOLOGY TIP
To find the argument u, use the ANGLE
or ARG key in the same menu/submenu
as the ABS key [except on HP-39gs,
where it is in MATH/COMPLEX].
r
(a, b)
θ
Figure 9–2
Polar
Form
Every complex number a bi can be written in polar form:
r(cos u i sin u),
where r a bi
a
2
b
2
, a r cos u, and b r sin u.
When a complex number is written in polar form, the argument u is not uniquely
determined, since u, u 2p, u 4p, etc., all satisfy the conditions in the box.
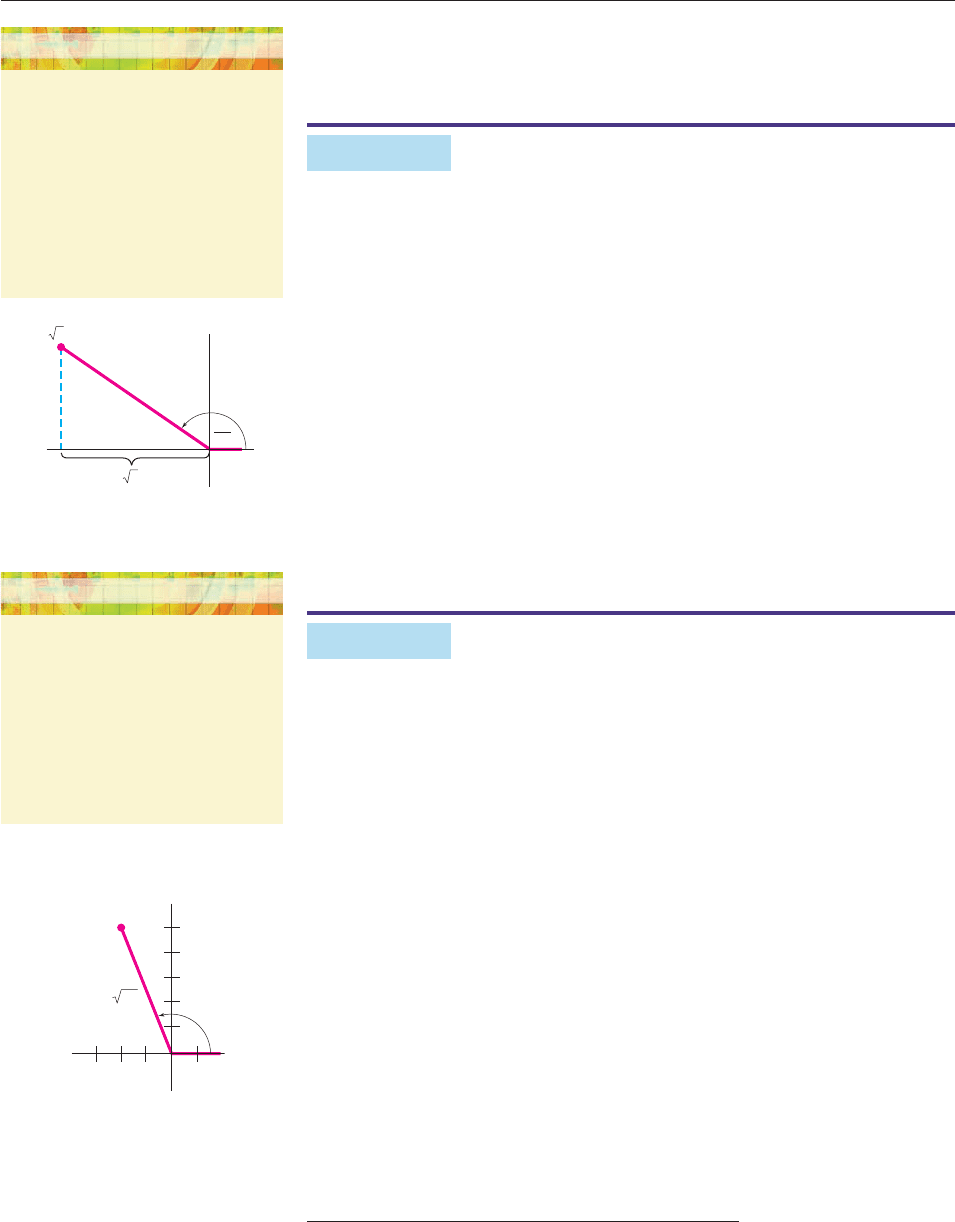
EXAMPLE 2
Express 3
i in polar form.
SOLUTION Here a 3
and b 1, so
r
a
2
b
2
(3
)
2
1
2
3 1
2.
The angle u must satisfy
cos u
a
r
2
3
and sin u
b
r
1
2
.
Since 3
i lies in the second quadrant (Figure 9–3), u must be a second-
quadrant angle. Our knowledge of special angles and Figure 9–3 show that
u 5p/6 satisfies these conditions. Hence,
3
i 2
cos
5
6
p
i sin
5
6
p
. ■
EXAMPLE 3*
Express 2 5i in polar form.
SOLUTION Since a 2 and b 5, r
(2)
2
5
2
29. The angle u
must satisfy
cos u
a
r
2
2
9
and sin u
b
r
5
29
,
so
tan u
c
s
o
in
s
u
u
5
2
/
/
2
2
9
9
5
2
2.5.
Since 2 5i lies in the second quadrant (Figure 9–4), u lies between p/2 and
p. As we saw in Section 7.5, the only solution of the equation tan u 2.5 that
lies between p/2 and p is u 1.1903 p 1.9513. Therefore,
2 5i 29(cos 1.9513 i sin 1.9513). ■
Multiplication and division of complex numbers in polar form are done by
the following rules, which are proved at the end of the section.
628 CHAPTER 9 Applications of Trigonometry
TECHNOLOGY TIP
The complex number
r (cos u i sin u)
is entered in a calculator as follows:
TI-84+: re
iu
[Use the special i key.]
TI-86/89: (r ⬔ u)
[⬔ is on the keyboard]
–
3 + i
1
2
3
5π
6
Figure 9–3
TECHNOLOGY TIP
To convert from rectangular to polar
form, or vice versa, use
POL or
RECT in this menu/submenu:
TI-84+: MATH/CPX
TI-86: CPLX
TI-89: MATH/MATRIX/
VECTOR OPS
*Omit this example if you haven’t read Section 7.5.
θ
−2 + 5i
29
Figure 9–4

SECTION 9.1 The Complex Plane and Polar Form for Complex Numbers 629
In other words, to multiply two numbers in polar form, just multiply the moduli
and add the arguments. To divide, just divide the moduli and subtract the argu-
ments. Before proving the statements in the box, we will illustrate them with some
examples.
EXAMPLE 4
Find z
1
z
2
, when
z
1
2[cos(5p/6) i sin(5p/6)] and z
2
3[cos(7p/4) i sin(7p/4)].
SOLUTION Here r
1
is the number 2, and u
1
5p/6; similarly, r
2
3, and
u
2
7p/4, and we have
z
1
z
2
r
1
r
2
[cos(u
1
u
2
) i sin(u
1
u
2
)]
2
3
cos
5
6
p
7
4
p
i sin
5
6
p
7
4
p
6
cos
1
1
0
2
p
2
1
1
2
p
i sin
1
1
0
2
p
2
1
1
2
p
6
cos
3
1
1
2
p
i sin
3
1
1
2
p
. ■
EXAMPLE 5
Find z
1
/z
2
, where
z
1
10[cos(p/3) i sin(p/3)] and z
2
2[cos(p/4) i sin(p/4)].
SOLUTION
z
z
1
2
1
2
0
cos
p
3
p
4
i sin
p
3
p
4
5
cos
1
p
2
i sin
1
p
2
. ■
10
cos
p
3
i sin
p
3
2
cos
p
4
i sin
p
4
Polar Multiplication and
Division Rules
If z
1
r
1
(cos u
1
i sin u
1
) and z
2
r
2
(cos u
2
i sin u
2
) are any two com-
plex numbers, then
z
1
z
2
r
1
r
2
[cos(u
1
u
2
) i sin(u
1
u
2
)]
and
z
z
1
2
r
r
1
2
[cos(u
1
u
2
) i sin(u
1
u
2
)] (z
2
0).
TECHNOLOGY TIP
Complex arithmetic can be done with
numbers in polar form on TI calcula-
tors. Some answers may be expressed
in rectangular form.

PROOF OF THE POLAR MULTIPLICATION RULE
If z
1
r
1
(cos u
1
i sin u
1
) and z
2
r
2
(cos u
2
i sin u
2
), then
z
1
z
2
r
1
(cos u
1
i sin u
1
)r
2
(cos u
2
i sin u
2
)
r
1
r
2
(cos u
1
i sin u
1
)(cos u
2
i sin u
2
)
r
1
r
2
(cos u
1
cos u
2
i sin u
1
cos u
2
i cos u
1
sin u
2
i
2
sin u
1
sin u
2
)
r
1
r
2
[(cos u
1
cos u
2
sin u
1
sin u
2
) i(sin u
1
cos u
2
cos u
1
sin u
2
)].
But the addition identities for sine and cosine (page 524) show that
cos u
1
cos u
2
sin u
1
sin u
2
cos(u
1
u
2
)
sin u
1
cos u
2
cos u
1
sin u
2
sin(u
1
u
2
).
Therefore,
z
1
z
2
r
1
r
2
[(cos u
1
cos u
2
sin u
1
sin u
2
) i(sin u
1
cos u
2
cos u
1
sin u
2
)]
r
1
r
2
[cos(u
1
u
2
) i sin(u
1
u
2
)].
This completes the proof of the multiplication rule. The division rule is proved
similarly (Exercise 77).
630 CHAPTER 9 Applications of Trigonometry
EXERCISES 9.1
In Exercises 1–8, plot the point in the complex plane corre-
sponding to the number.
1. 3 2i 2. 7 6i
3.
8
3
5
3
i 4. 2
7i
5. (1 i)(1 i ) 6. (2 i)(1 2i)
7. 2i
3
5
2
i
8.
4
3
i
(6 3i)
In Exercises 9–14, find the absolute value.
9. 5 12i 10. 2i 11. 1 2
i
12. 2 3i 13. 12i 14. i
7
15. Give an example of complex numbers z and w such that
z w z w.
16. If z 3 4i, find z
2
and zz
, where z
is the conjugate of z
(see page 323).
In Exercises 17–24, sketch the graph of the equation in the com-
plex plane (z denotes a complex number of the form a bi).
17. z 4 [Hint: The graph consists of all points that lie 4 units
from the origin.]
18. z 1
19. z 1 10 [Hint: 1 corresponds to (1, 0) in the complex
plane. What does the equation say about the distance from z
to 1?]
20. z 3 1 21. z 2i 4
22. z 3i 2 9 [Hint: Rewrite it as z (2 3i) 9.]
23. Re(z) 2 [The real part of the complex number
z a bi is defined to be the number a and is denoted
Re(z).]
24. Im(z) 5/2 [The imaginary part of z a bi is de-
fined to be the number b (not bi) and is denoted Im(z).]
In Exercises 25–36, express the number in the form a bi.
25. 2
cos
p
4
i sin
p
4
26. 3
cos
p
3
i sin
p
3
27. cos
p
2
i sin
p
2
28. 4
cos
3
4
p
i sin
3
4
p
29. 5
cos
2
3
p
i sin
2
3
p
30. 2
cos
7
6
p
i sin
7
6
p
31. 1.5
cos
p
6
i sin
p
6
32. 5(cos 3 i sin 3)
33. 2(cos 4 i sin 4) 34. 3(cos 5 i sin 5)
35. 4(cos 2 i sin 2) 36. 2(cos 1.5 i sin 1.5)
In Exercises 37–52, express the number in polar form.
37. 3 3i 38. 5 5i 39. 2 23
i
40. 53
5i 41. 33
3i 42. 4 43
i

SECTION 9.1 The Complex Plane and Polar Form for Complex Numbers 631
43. 3
3
i 44. 25
25
i
45. 3 4i 46. 4 3i 47. 5 12i
48. 7
3i 49. 1 2i 50. 3 5i
51.
5
2
7
2
i 52. 5
11i
In Exercises 53–64, perform the indicated multiplication
or division. Express your answer in both polar form
r(cos u i sin u) and rectangular form a bi.
53.
cos
p
2
i sin
p
2
(cos p i sin p)
54. 2
cos
p
6
i sin
p
6
5
cos
p
3
i sin
p
3
55. 4
cos
p
4
i sin
p
4
3
cos
1
p
2
i sin
1
p
2
56.
cos
1
p
2
i sin
1
p
2
2
cos
7
1
p
2
i sin
7
1
p
2
57. 3
cos
p
8
i sin
p
8
12
cos
3
8
p
i sin
3
8
p
58. 12
cos
1
1
1
2
p
i sin
1
1
1
2
p
7
2
cos
p
4
i sin
p
4
59.
60.
61.
62.
63.
64.
In Exercises 65–72, convert to polar form and then multiply or
divide. Express your answer in polar form.
65. (1 i)(1 3
i) 66. (1 i)(3 3i)
54
cos
9
4
p
i sin
9
4
p
6
cos
7
1
p
2
i sin
7
1
p
2
6
cos
7
2
p
0
i sin
7
2
p
0
4
cos
1
p
0
i sin
1
p
0
8
cos
5
1
p
8
i sin
5
1
p
8
4
cos
p
9
i sin
p
9
8
cos
4
3
p
i sin
4
3
p
4
cos
7
6
p
i sin
7
6
p
cos
3
4
p
i sin
3
4
p
cos
p
4
i sin
p
4
cos p i sin p
cos
2
3
p
i sin
2
3
p
67.
1
1
i
i
68.
2
1
2i
i
69. 3i(2 3
2i) 70.
3
4
i
i
71. i(i 1)(3
i)
72. (1 i)(2 3
2i)(4 4 3
i)
73. Explain what is meant by saying that multiplying a complex
number z r (cos u i sin u) by i amounts to rotating z 90°
counterclockwise around the origin. [Hint: Express i and iz
in polar form. What are their relative positions in the com-
plex plane?]
74. Describe what happens geometrically when you multiply a
complex number by 2.
THINKERS
75. The sum of two distinct complex numbers, a bi and
c di, can be found geometrically by means of the so-
called parallelogram rule: Plot the points a bi and
c di in the complex plane, and form the parallelogram,
three of whose vertices are 0, a bi, and c di, as in the
figure. Then the fourth vertex of the parallelogram is the
point whose coordinate is the sum
(a bi) (c di) (a c) (b d)i.
Complete the following proof of the parallelogram rule
when a 0 and c 0.
(a) Find the slope of the line K from 0 to a bi. [Hint: K
contains the points (0, 0) and (a, b).]
(b) Find the slope of the line N from 0 to c di.
(c) Find the equation of the line L through a bi and par-
allel to line N of part (b). [Hint: The point (a, b) is on L;
find the slope of L by using part (b) and facts about the
slope of parallel lines.]
(d) Find the equation of the line M through c di and par-
allel to line K of part (a).
(e) Label the lines K, L, M, and N in the figure.
(f ) Show by using substitution that the point (a c, b d)
satisfies both the equation of line L and the equation of
line M. Therefore, (a c, b d ) lies on both L and M.
Since the only point on both L and M is the fourth vertex
of the parallelogram (see the figure), this vertex must be
(a c, b d). Hence, this vertex has coordinate
(a c) (b d)i (a bi) (c di).
76. Let z a bi be a complex number and denote its conju-
gate a bi by z
. Prove that z
2
zz
.
0
a + bi
a + bic + di
0
c + di

632 CHAPTER 9 Applications of Trigonometry
77. Proof of the polar division rule. Let z
1
r
1
(cos u
1
i sin u
1
)
and z
2
r
2
(cos u
2
i sin u
2
). Then
z
z
1
2
.
(a) Multiply out the denominator on the right side and use the
Pythagorean identity to show that it is just the number r
2
.
(b) Multiply out the numerator on the right side; use the
subtraction identities for sine and cosine (page 524) to
show that it is
r
1
[cos(u
1
u
2
) i sin(u
1
u
2
)].
Therefore,
z
z
1
2
r
r
1
2
[cos(u
1
u
2
) i sin(u
1
u
2
)].
cos u
2
i sin u
2
cos u
2
i sin u
2
r
1
(cos u
1
i sin u
1
)
r
2
(cos u
2
i sin u
2
)
r
1
(cos u
1
i sin u
1
)
r
2
(cos u
2
i sin u
2
)
78. (a) If s(cos b i sin b) r(cos u i sin u), (with
r 0, s 0), explain why we must have s r. [Hint:
Think distance.]
(b) If r(cos b i sin b) r(cos u i sin u), explain why
cos b cos u and sin b sin u. [Hint: See property 5
of the complex numbers on page 322.]
(c) If cos b cos u and sin b sin u, show that angles b
and u in standard position have the same terminal side.
[Hint: (cos b, sin b) and (cos u, sin u) are points on the
unit circle.]
(d) Use parts (a)–(c) to prove this equality rule for polar
form:
s(cos b i sin b)
r(cos u i sin u)
exactly when s r and b u 2kp for some integer
k. [Hint: Angles with the same terminal side must differ
by an integer multiple of 2p.]
9.2 DeMoivre’s Theorem and nth Roots of Complex Numbers
■ Use DeMoivre’s Theorem to compute powers of complex numbers.
■ Find the nth roots of a complex number.
■ Find the nth roots of unity algebraically and geometrically.
Polar form provides a convenient way to calculate both powers and roots of com-
plex numbers. If z r(cos u i sin u), then the multiplication formula on page
629 shows that
z
2
z
z r
r[cos(u u) i sin(u u)]
r
2
(cos 2u i sin 2u).
Similarly,
z
3
z
2
z r
2
r[cos(2u u) i sin(2u u)]
r
3
(cos 3u i sin 3u).
Repeated application of the multiplication formula proves the following theorem.
EXAMPLE 1
Compute (3
i)
5
.
SOLUTION We first express 3
i in polar form (as in Example 2 on
page 628):
3
i 2
cos
5
6
p
i sin
5
6
p
.
Section Objectives
DeMoivre’s
Theorem
For any complex number z r (cos u i sin u) and any positive integer n,
z
n
r
n
(cos nu i sin nu).
By DeMoivre’s Theorem,
(3
i)
5
2
5
cos
5
5
6
p
i sin
5
5
6
p
32
cos
25
6
p
i sin
25
6
p
.
Since 25p/6 (p/6) (24p/6) (p/6) 4p, we have
(3
i)
5
32
cos
25
6
p
i sin
25
6
p
32
cos
p
6
i sin
p
6
32
2
3
1
2
i
16 3
16i. ■
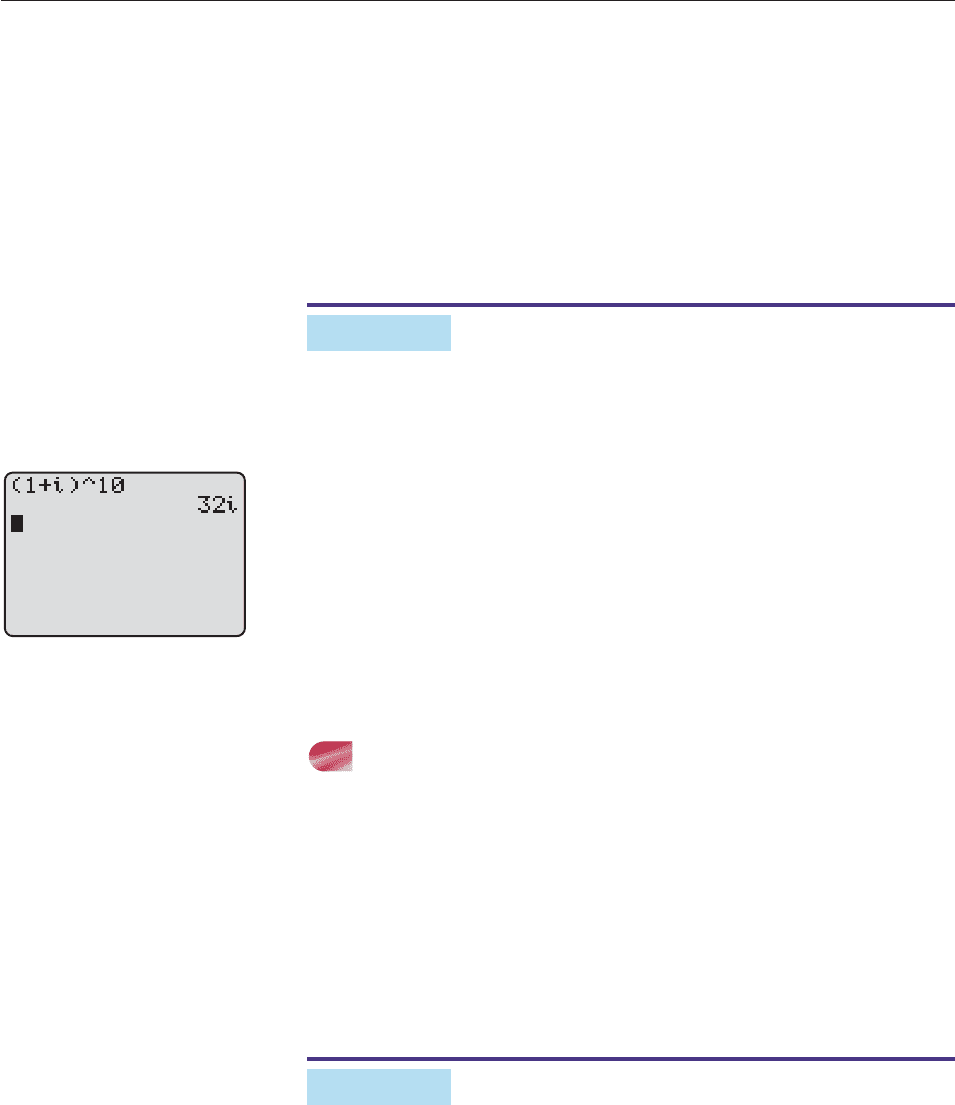
EXAMPLE 2
Find (1 i)
10
.
SOLUTION First verify that the polar form of 1 i is
1 i 2
cos
p
4
i sin
p
4
.
Therefore, by DeMoivre’s Theorem,
(1 i)
10
(2
)
10
cos
10
4
p
i sin
10
4
p
(2
1/2
)
10
cos
5
2
p
i sin
5
2
p
2
5
(0 i
1) 32i.
A calculator that can do complex arithmetic confirms this result (Figure 9–5). ■
nTH ROOTS
Recall that for a real number c, we called a solution of the equation x
n
c an nth
root of c. Similarly, if a bi is a complex number, then any solution of the equation
z
n
a bi
is called an nth root of a bi. In this context, the radical symbol will be used
only for nonnegative real numbers and will have the same meaning as before: If r
is a nonnegative real number, then
n
r
denotes the unique nonnegative real num-
ber whose nth power is r.
All nth roots of a complex number a bi can easily be found if a bi is writ-
ten in polar form, as illustrated in the next example.
EXAMPLE 3
Find the fourth roots of 8 8 3
i.
SOLUTION To solve z
4
8 8 3
i, first verify that the polar form of
8 8 3
i is 16
cos
2
3
p
i sin
2
3
p
. We must find numbers s and b such that
[s(cos b i sin b)]
4
16
cos
2
3
p
i sin
2
3
p
.
SECTION 9.2 DeMoivre’s Theorem and nth Roots of Complex Numbers 633
Figure 9–5

By DeMoivre’s Theorem, we must have
s
4
(cos 4b i sin 4b) 16
cos
2
3
p
i sin
2
3
p
.
The equality rules for complex numbers in polar form (Exercise 78 in Section 9.1)
show that this can happen only when
s
4
16 and 4b
2
3
p
2kp (k an integer)
s
4
16 2 b
2p/3
4
2kp
.
Substituting these values in s(cos b i sin b) shows that the solutions of
z
4
16
cos
2
3
p
i sin
2
3
p
are
z 2
cos
2p/3
4
2kp
i sin
2p/3
4
2kp
(k 0, 1, 2, 3, . . .).
which can be simplified as
z 2
cos
p
6
k
2
p
i sin
p
6
k
2
p
(k 0, 1, 2, 3, . . .).
Letting k 0, 1, 2, 3, produces four distinct solutions:
k 0: z 2
cos
p
6
i sin
p
6
3
i.
k 1: z 2
cos
p
6
p
2
i sin
p
6
p
2
2
cos
2
3
p
i sin
2
3
p
1 3
i.
k 2: z 2
cos
p
6
p
i sin
p
6
p
2
cos
7
6
p
i sin
7
6
p
3
i.
k 3: z 2
cos
p
6
3
2
p
i sin
p
6
3
2
p
2
cos
5
3
p
i sin
5
3
p
.
1 3
i.
Any other value of k produces an angle b with the same terminal side as one of the
four angles used above, and hence leads to the same solution. For instance,
when k 4, then b
p
6
4
2
p
p
6
2p and b has the same terminal side as
p/6. Therefore, we have found all the solutions—the four fourth roots of
8 8 3
i.* ■
The general equation z
n
r(cos u i sin u) can be solved by exactly the
same method used in the preceding example—just substitute n for 4, r for 16, and
u for 2p/3, as follows. A solution is a number s(cos b i sin b) such that
[s(cos b i sin b)]
n
r(cos u i sin u)
s
n
(cos nb i sin nb) r(cos u i sin u).
634 CHAPTER 9 Applications of Trigonometry
*Alternatively, page 330 shows that a fourth-degree equation, such as z
4
8 8 3
i, has at most
four distinct solutions.

Therefore,
s
n
r and nb u 2kp (k any integer)
s
n
r
b
u
n
2kp
Taking k 0, 1, 2, . . . , n 1 produces n distinct angles b. Any other value of k
leads to an angle b with the same terminal side as one of these. Hence,
SECTION 9.2 DeMoivre’s Theorem and nth Roots of Complex Numbers 635
Formula for
nth Roots
For each positive integer n, nonzero complex number
r(cos u i sin u)
has exactly n distinct nth roots. They are given by
n
r
cos
u
n
2kp
i sin
u
n
2kp
,
where k 0, 1, 2, 3, . . . n 1.
EXAMPLE 4
Find the fifth roots of 4 4i.
SOLUTION First write 4 4i in polar form as 42
cos
p
4
i sin
p
4
. Now
apply the root formula with n 5, r 42
, u p/4, and k 0, 1, 2, 3, 4.
Note that
5
r
5
4 2
(4 2
)
1/5
(2
2
2
1/2
)
1/5
(2
5/2
)
1/5
2
5/10
2
1/2
2
.
Therefore, the fifth roots are
2
cos
p/4
5
2kp
i sin
p/4
5
2kp
k 0, 1, 2, 3, 4,
that is,
k 0: 2
cos
p/4
5
0
i sin
p/4
5
0
2
cos
2
p
0
i sin
2
p
0
,
k 1: 2
cos
p/4
5
2p
i sin
p/4
5
2p
2
cos
9
2
p
0
i sin
9
2
p
0
,
k 2: 2
cos
p/4
5
4p
i sin
p/4
5
4p
2
cos
1
2
7
0
p
i sin
1
2
7
0
p
,
k 3: 2
cos
p/4
5
6p
i sin
p/4
5
6p
2
cos
2
2
5
0
p
i sin
2
2
5
0
p
,
k 4: 2
cos
p/4
5
8p
i sin
p/4
5
8p
2
cos
3
2
3
0
p
i sin
3
2
3
0
p
.
■
TECHNOLOGY TIP
The polynomial solvers on TI-86 and
HP-39gs can solve
z
5
4 4i
and similar equations.
On TI-89, use cSOLVE in the
COMPLEX submenu of the ALGEBRA
menu.
