Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


*See the Technology Tip on page 681.
This is the situation in the box, with h 4 and k 3. So the graph is a
parabola with vertex (4, 3). Its focus is on the horizontal line y 3. There
are several ways to graph this parabola.
Method 1. The equation of this parabola can be obtained from the equation
y
2
1
3
x by replacing x with x 4 x (4) and y with y 3 y (3). So
its graph is the parabola y
2
1
3
x (Figure 10–38) shifted 4 units to the left and
3 units downward, as shown in Figure 10–41.
Figure 10–41
Method 2. To use technology for the graph, we first solve the equation for y:
(y 3)
2
x
3
4
Take square roots on both sides: y 3
x
3
4
Subtract 3 from both sides: y
x
3
4
3.
Graphing
y
x
3
4
3 and y
x
3
4
3
on the same screen produces the graph in Figure 10–42.
Method 3. To use a conic section grapher*, you must have the equation in the
form given in the preceding box and find the value of p:
(y k)
2
4p(x h)
[y (3)]
2
1
3
[x (4)].
Therefore,
4p
1
3
Multiply both sides by
1
4
: p
1
1
2
.
Now insert the appropriate values (h 4, k 3, and p 1/12) in the conic
section grapher to obtain Figure 10–42. ■
2
2
4
2
4
6
4646 2
x
y
706 CHAPTER 10 Analytic Geometry
3
6
5
6
Figure 10–42

EXAMPLE 8
Find the focus and directrix of the parabola (y 3)
2
x
3
4
whose graph was
found in Example 7.
SOLUTION As we saw in Example 7, the parabola (y 3)
2
x
3
4
has vertex
(4, 3) and can be obtained by shifting the parabola y
2
1
3
x 4 units to the left
and 3 units downward. In Example 5 we found that the parabola y
2
1
3
x has
focus (p, 0) (1/12, 0) and directrix the vertical line x p 1/12.
Therefore, the focus of (y 3)
2
x
3
4
is obtained as follows:
Shift 4 units left and
3 units downward
1
1
2
, 0
----------------------------->
1
1
2
4, 0 3
4
1
7
2
, 3
The directrix is obtained similarly by shifting the vertical line x
1
1
2
four units
to the left, which gives the line x
1
1
2
4
4
1
9
2
. ■
Examples 6–8 illustrate the following facts.
SECTION 10.3 Parabolas 707
Standard Equations
of Parabolas with
Vertex at (h, k)
If p is a nonzero real number, then the graph of each of the following equa-
tions is a parabola with vertex (h, k).
focus: (h, p k)
directrix: the horizontal line y p k
(x h)
2
4p(y k)
axis: the vertical line x h
opens upward if p 0, downward if p 0
focus: (p h, k)
directrix: the vertical line x p h
(y k)
2
4p(x h)
axis: the horizontal line y k
opens to right if p 0, to left if p 0
GRAPHING TECHNIQUES
When the equation of a parabola is not in standard form, it can be graphed directly
on a calculator or computer without finding the standard form.
EXAMPLE 9
Graph the equation x 5y
2
30y 41 without putting it in standard form.
SOLUTION We rewrite the equation as
5y
2
30y 41 x 0.
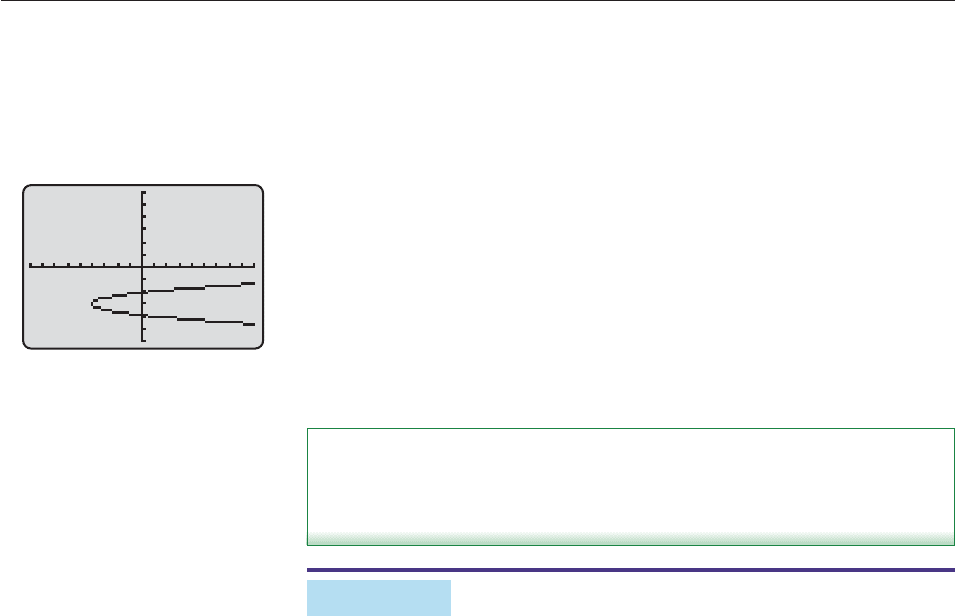
This is a quadratic equation of the form ay
2
by c 0, with a 5, b 30,
and c 41 x. It can be solved by using the quadratic formula.
y
b
2a
b
2
4
ac
.
Now graph both
y and y
on the same screen to obtain the parabola in Figure 10–43 (see the second Tech-
nology Tip on page 681). ■
EXAMPLE 10
Find the vertex, focus, and directrix of the parabola
x 5y
2
30y 41
that was graphed in Example 9.
SOLUTION We first rewrite the equation.
5y
2
30y 41 x
Subtract 41 from both sides: 5y
2
30y x 41
Factor out 5 on left side: 5( y
2
6y) x 41.
Complete the square on the expression y
2
6y by adding 9 (the square of half the
coefficient of y):
5(y
2
6y 9) x 41 ?.
On the left side, we have actually added 5
9 45, so we must add the same
amount to the right side.
5(y
2
6y 9) x 41 45
Factor left side: 5(y 3)
2
x 4
Divide both sides by 5: (y 3)
2
1
5
(x 4)
[y (3)]
2
1
5
[x (4)].
Thus, the graph is a parabola with vertex (4, 3). In this case, 4p 1/5, so
p 1/20 .05. Hence, the focus is (.05 4, 3) (3.95, 3), and the
directrix is x 4 .05 4.05. ■
30 900
20(41
x)
10
30 900
20(41
x)
10
30 900
20(41
x)
10
30
30
2
4
5(4
1 x)
2
5
708 CHAPTER 10 Analytic Geometry
NOTE
Parametric equations for parabolas are discussed in Special Topics 10.3.A and summarized in the
endpapers at the beginning of the book.
−6
9
6
−9
Figure 10–43
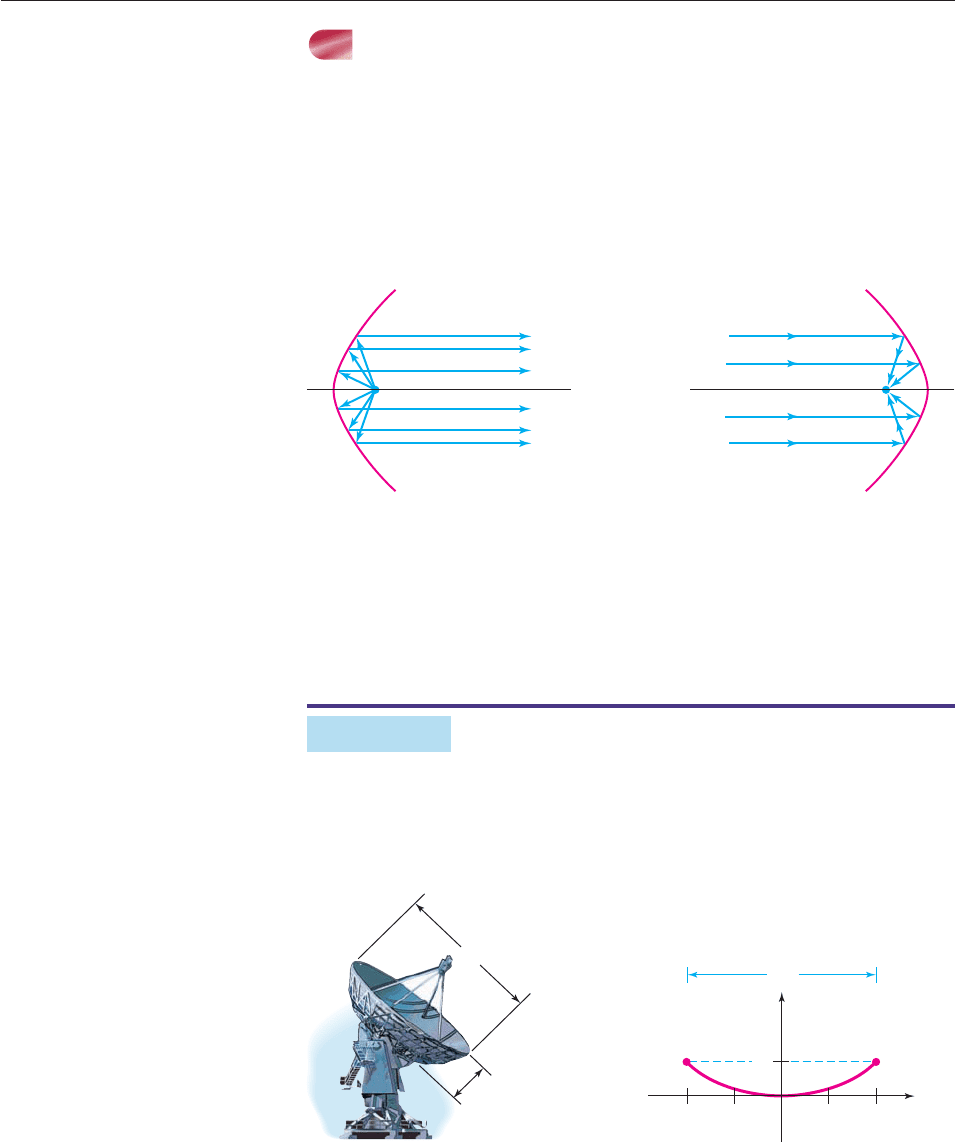
APPLICATIONS
Certain laws of physics show that sound waves or light rays from a source at the
focus of a parabola will reflect off the parabola in rays parallel to the axis of the
parabola, as shown in Figure 10– 44. This is the reason that parabolic reflectors
are used in automobile headlights and searchlights.
Conversely, a light ray coming toward a parabola will be reflected into the
focus, as shown in Figure 10–45. This fact is used in the design of radar antennas,
satellite dishes, and field microphones used at outdoor sporting events to pick up
conversation on the field.
Figure 10–44 Figure 10–45
Projectiles follow a parabolic curve, a fact that is used in the design of water
slides in which the rider slides down a sharp incline, then up and over a hill,
before plunging downward into a pool. At the peak of the hill, the rider shoots up
along a parabolic arc several inches above the slide, experiencing a sensation of
weightlessness.
EXAMPLE 11
The radio telescope in Figure 10–46 has the shape of a parabolic dish (a cross sec-
tion through the center of the dish is a parabola). It is 30 feet deep at the center and
has a diameter of 200 feet. How far from the vertex of the parabolic dish should
the receiver be placed to catch all the rays that hit the dish?
Figure 10–46 Figure 10–47
SOLUTION Rays hitting the dish are reflected into the focus, as explained
above. So the radio receiver must be located at the focus. To find the focus, draw
a cross section of the dish, with vertex at the origin, as in Figure 10–47. The
100
(−100, 30) (100, 30)
200
50
30
−50−100
x
y
200
30
Axis
Focus
Axis
Focus
SECTION 10.3 Parabolas 709
equation of this parabola is of the form x
2
4py. Since the point (100, 30) is on
the parabola, we have
x
2
4py
Substitute: 100
2
4p(30)
Simplify: 120p 100
2
Divide both sides by 120: p
1
1
0
2
0
0
2
Simplify: p
25
3
0
.
As we saw in the box on page 701, the focus is the point (0, p), which is p units
from the vertex (0, 0). Therefore, the receiver should be placed 250/3 83.33
feet from the vertex. ■
710 CHAPTER 10 Analytic Geometry
EXERCISES 10.3
In Exercises 1–6, determine which of the following equations
could possibly have the given graph.
y x
2
/4, x
2
8y,6x y
2
, y
2
4x,
2x
2
y
2
12, x
2
6y
2
18,
6y
2
x
2
6, 2x
2
y
2
8
1. 2.
3.
y
x
y
x
y
x
4.
5. 6.
In Exercises 7–10, find the equation of the parabola.
7. focus (4, 0); directrix x 4
8. focus (5, 0); directrix x 5
9. focus (0, 8); directrix y 8
10. focus (0, 7); directrix y 7
x
y
x
y
y
x
SECTION 10.3 Parabolas 711
In Exercises 11–16, find the focus and directrix of the
parabola.
11. y 3x
2
12. x .5y
2
13. y .25x
2
14. x 6y
2
15. y
2
8x 0 16. x
2
3y 0
In Exercises 17–28, determine the vertex, focus, and directrix
of the parabola without graphing and state whether it opens
upward, downward, left, or right.
17. x y
2
2 18. y 3 x
2
19. x (y 1)
2
2 20. y (x 2)
2
3
21. 3x 2 (y 3)
2
22. 2x 1 6(y 1)
2
23. x y
2
9y 24. x y
2
y 1
25. y 3x
2
x 4 26. y 3x
2
4x 1
27. y 3x
2
4x 5 28. y 2x
2
x 1
In Exercises 29–34, find the latus rectum of the parabola
whose equation is given. [Hint: Examples 3 and 4 may be help-
ful in Exercises 29–30.]
29. x
2
8y 30. y
2
x/3
31. y
2
20x 32. y 2x
2
33. x
2
4y 0 34. y
2
12x 0
In Exercises 35–42, sketch the graph of the equation and label
the vertex.
35. y 4(x 1)
2
2 36. y 3(x 2)
2
3
37. x 2(y 2)
2
38. x 3(y 1)
2
2
39. y x
2
4x 1 40. y x
2
8x 6
41. y x
2
2x 42. x y
2
3y
In Exercises 43–54, find the equation of the parabola satisfying
the given conditions.
43. Vertex (0, 0); axis x 0; (2, 12) on graph.
44. Vertex (0, 1); axis x 0; (2, 7) on graph.
45. Vertex (1, 0); axis x 1; (2, 13) on graph.
46. Vertex (3, 0); axis y 0; (1, 1) on graph.
47. Vertex (2, 1); axis y 1; (5, 0) on graph.
48. Vertex (1, 3); axis y 3; (1, 4) on graph.
49. Vertex (3, 2); focus (47/16, 2).
50. Vertex (5, 5); focus (5, 99/20).
51. Vertex (1, 1); focus (1, 9/8).
52. Vertex (4, 3); (6, 2) and (6, 4) on graph.
53. Vertex (1, 3); (8, 0) and (0, 4) on graph.
54. Vertex (1, 3); (0, 1) and (1, 5) on graph.
In Exercises 55–62, identify the conic section whose equation
is given, list its vertex or vertices, if any, and find its graph.
55. x
2
6x y 5 56. y
2
x 2y 2
57. 3y
2
x 1 2y 58. 2y
2
x 4y 5
59. 3x
2
3y
2
6x 12y 6 0
60. 2x
2
3y
2
12x 6y 9 0
61. 2x
2
y
2
16x 4y 24 0
62. 4x
2
40x 2y 105 0
In Exercises 63–68, determine which of the following equations
could possibly have the given graph.
y (x 5)
2
3, x (y 3)
2
2,
y (x 4)
2
2, x (y 3)
2
2.
y
2
4y x 1, y x
2
8x 18
63.
64.
65.
66.
712 CHAPTER 10 Analytic Geometry
67.
68.
69. Find the number b such that the vertex of the parabola
y x
2
bx c lies on the y-axis.
70. Find the number d such that the parabola (y 1)
2
dx 4
passes through (6, 3).
71. Find the points of intersection of the parabola
4y
2
4y 5x 12 and the line x 9.
72. Find the points of intersection of the parabola
4x
2
8x 2y 5 and the line y 15.
73. Let p be a real number.
(a) Show that the endpoints of the latus rectum of the
parabola with equation y
2
4px are (p, 2p) and
(p,2p).
(b) Show that the endpoints of the latus rectum of the
parabola with equation x
2
4py are (2p, p) and
(2p, p).
74. Show that the length of the latus rectum of the parabola with
equation y
2
4px or x
2
4py is 4p. [Hint: Exercise 73.]
75. A parabolic satellite dish is 4 feet in diameter and 1.5 feet
deep. How far from the vertex should the receiver be placed
to catch all the signals that hit the dish?
76. A flashlight has a parabolic reflector that is 3 inches in
diameter and 1.5 inches deep. For the light from the bulb to
reflect in beams that are parallel to the center axis of the
4
1.5
flashlight, how far from the vertex of the reflector should
the bulb be located? [Hint: See Figure 10–44 and the pre-
ceding discussion.]
77. A radio telescope has a parabolic dish with a diameter of
300 feet. Its receiver (focus) is located 130 feet from the
vertex. How deep is the dish at its center? [Hint: Position
the dish as in Figure 10–47, and find the equation of the
parabola.]
78. The 6.5-meter MMT telescope on top of Mount Hopkins in
Arizona has a parabolic mirror. The focus of the parabola is
8.125 meters from the vertex of the parabola. Find the depth
of the mirror.
79. The Hale telescope at Mount Palomar in California also has a
parabolic mirror, whose depth is .096 meter (see the figure for
Exercise 78). The focus of the parabola is 16.75 meters from
the vertex. Find the diameter of the mirror.
80. A large spotlight has a parabolic reflector that is 3 feet deep
at its center. The light source is located 1
1
3
feet from the vertex.
What is the diameter of the reflector?
81. The cables of a suspension bridge are shaped like parabolas.
The cables are attached to the towers 100 feet from the bridge
surface, and the towers are 420 feet apart. The cables touch
the bridge surface at the center (midway between the towers).
At a point on the bridge 100 feet from one of the towers, how
far is the cable from the bridge surface?
82. At a point 120 feet from the center of a suspension bridge, the
cables are 24 feet above the bridge surface. Assume that
the cables are shaped like parabolas and touch the bridge sur-
face at the center (which is midway between the towers). If
the towers are 600 feet apart, how far above the surface of the
bridge are the cables attached to the towers?
6.5 m
Depth
Focus
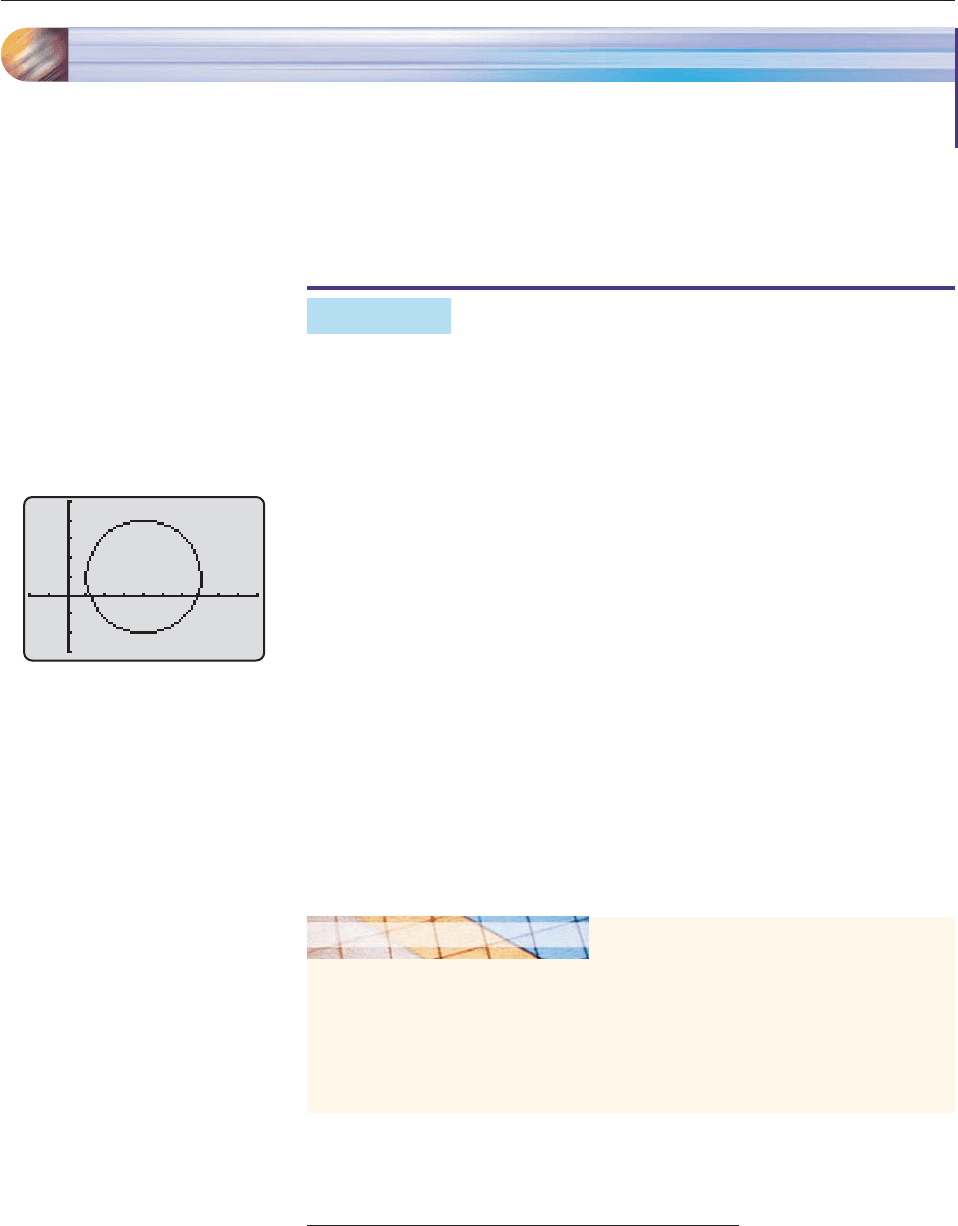
SPECIAL TOPICS 10.3.A Parametric Equations for Conic Sections 713
■ Use parametric equations to represent and graph circles,
ellipses, hyperbolas, and parabolas.
Graphing conic sections parametrically is often easier than using the graphing
methods discussed in Section 10.1–10.3. Furthermore, parametric graphs have
fewer erroneous gaps on a calculator screen.
EXAMPLE 1
Graph the curve given by the parametric equations
(
*
) x 3 cos t 4 and y 3 sin t 1(0 t 2p).
Show that the graph is the circle with center at (4, 1) and radius 3.
SOLUTION Figure 10–48 shows the curve given by the parametric equations.
The circle with center (4, 1) and radius 3 is the graph of the rectangular equation
(x 4)
2
( y 1)
2
9.
For every point (x, y) with x 3 cos t 4 and y 3 sin t 1, we have
(x 4)
2
(y 1)
2
(3 cos t 4 4)
2
(3 sin t 1 1)
2
(3 cos t)
2
(3 sin t)
2
9 cos
2
t 9 sin
2
t
9(cos
2
t sin
2
t)
9(1) 9. [Pythagorean Identity]
So the coordinates of every point on the graph in Figure 10–48 satisfy the equa-
tion of the circle. Conversely, it can be shown that the coordinates of every point
on the circle satisfy the parametric equations. So the curve in Figure 10–48 is the
circle with center (4, 1) and radius 3. ■
If you replace 4, 1, and 3 in Example 1 with h, k, and r respectively, then the
same computation leads to the following result.
10.3.A SPECIAL TOPICS Parametric Equations for Conic Sections*
Section Objective
Solve the equation (x 4)
2
(y 1)
2
9 of the circle in Example 1 for y and
verify that
y
9 (x
4)
2
1ory 9 (x
4)
2
1.
Graph these two equations on the same screen in the same viewing window as
Figure 10–48. How does your graph compare with Figure 10–48?
GRAPHING EXPLORATION
*The prerequisites for this section are: Sections 10.1–10.3, parametric graphing (Special Topics 3.3.A),
and basic trigonometry (Sections 6.2, 6.3 and 6.6).
−3
−210
5
Figure 10–48

ELLIPSES
Parametric equations for an ellipse can be obtained in the same way that the ones
for the circle were.
EXAMPLE 2
Show that the curve given by the parametric equations
x 2 cos t 3 and y 5
sin t 6(0 t 2p)
is the ellipse with rectangular equation
(x
4
3)
2
(y
5
6)
2
1.
SOLUTION We use the Pythagorean identity to show that the coordinates
given by the parametric equations satisfy the rectangular equation
(x
4
3)
2
(y
5
6)
2
[2 co
4
s t]
2
[5
5
sin t]
2
4c
4
os
2
t
5s
5
in
2
t
cos
2
t sin
2
t 1.
Conversely, it can be shown that the coordinates of every point (x, y) on the graph
of the rectangular equation also satisfy the parametric equations. ■
If you use, h, k, a, and b in place of 3, 6, 2, and 5
, respectively, in Example 2,
then the same computation leads to this result.
EXAMPLE 3
Use parametric equations to graph 4x
2
25y
2
100.
[(5
sin t 6) 6]
2
5
[(2 cos t 3) 3]
2
4
714 CHAPTER 10 Analytic Geometry
Parametric Equations
of a Circle
The circle with center (h, k) and radius r is given by the parametric equations
x r cos t h and y r sin t k (0 t 2p).
Parametric
Equations
for Ellipses
The ellipse with equation
(x
a
2
h)
2
(y
b
2
k)
2
1
is given by the parametric equations
x a cos t h and y b sin t k (0 t 2p).
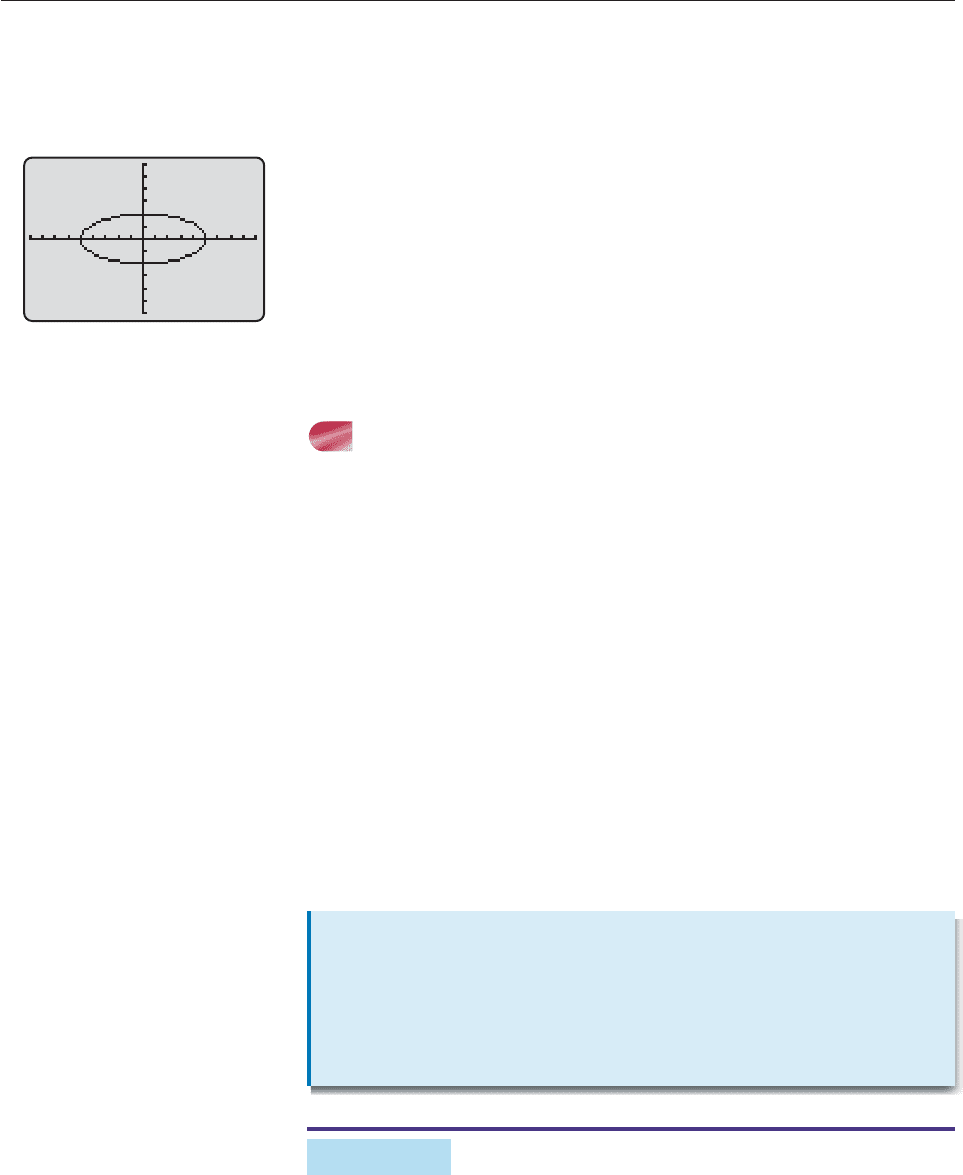
SOLUTION First, put the equation in standard form by dividing both sides
by 100.
1
4
0
x
0
2
2
1
5
0
y
0
2
1
1
0
0
0
0
2
x
5
2
y
4
2
1
x
5
2
2
y
2
2
2
1.
As the preceding box shows, this is the equation of an ellipse, with a 5 and
b 2. So its parametric equations are
x 5 cos t and y 2 sin t (0 t 2p).
Its graph is in Figure 10–49. ■
HYPERBOLAS
Consider the hyperbola with equation
(x
a
2
h)
2
(y
b
2
k)
2
1.
Its graph can be obtained from these parametric equations:
x a sec t h and y b tan t k (0 t 2p)
because, by the Pythagorean identity for secant and tangent,
(x
a
2
h)
2
(y
b
2
k)
2
[a se
a
c t]
2
[b t
b
an
2
t]
2
a
2
s
a
e
2
c
2
t
b
2
t
b
a
2
n
2
t
sec
2
t tan
2
t 1.
This proves the first of the following statements; the second is proved similarly.
EXAMPLE 4
Find parametric equations for the hyperbola with equation
y
9
2
1
x
6
2
1.
[(b tan t k) k]
2
b
2
[(a sec t h) h]
2
a
2
SPECIAL TOPICS 10.3.A Parametric Equations for Conic Sections 715
−99
−6
6
Figure 10–49
Parametric Equations
for Hyperbolas
Hyperbola Parametric Equations
(x
a
2
h)
2
(y
b
2
k)
2
1 x a sec t h
co
a
s t
h and y b tan t k
(0 t 2p)
(y
a
2
k)
2
(x
b
2
h)
2
1 x b tan t h and y a sec t k
co
a
s t
k
(0 t 2p)
