Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


(b) In this case,
r
(2)
2
4
2
20 25
and tan u
4
2
2.
Using the TAN
1
key, we find that u 1.1071 is an angle between p/2
and 0 with tangent 2. However, we want an angle between p/2 and p
because (2, 4) is in the second quadrant. Since tangent has period p,
tan(1.1071 p) tan(1.1071) 2.
Thus, 1.1071 p 2.0344 is an angle between p/2 and p whose tangent
is 2. Therefore, one pair of polar coordinates is (25
, 2.0344). ■
The technique used in Example 3 may be summarized as follows.
EQUATION CONVERSION
When an equation in rectangular coordinates is given, it can be converted to polar
coordinates by making the substitutions x r cos u and y r cos u. Converting
a polar equation to rectangular coordinates, however, is a bit trickier.
EXAMPLE 4
Find an equivalent rectangular equation for the given polar equation, and use it to
identify the shape of the graph.
(a) r 4 cos u (b) r
1
1
sin u
SOLUTION
(a) Rewrite the equation r 4 cos u as follows.
Multiply both sides by r: r
2
4r cos u
Substitute r
2
x
2
y
2
and r cos u x: x
2
y
2
4x
x
2
4x y
2
0
Add 4 to both sides: (x
2
4x 4) y
2
4
Factor: (x 2)
2
y
2
2
2
As we saw in Section 1.1, the graph of this equation is the circle with center
(2, 0) and radius 2.
746 CHAPTER 10 Analytic Geometry
Rectangular to
Polar Conversion
If the rectangular coordinates of a point are (x, y), let r x
2
y
2
. If
(x, y) lies in the first or fourth quadrant, then its polar coordinates are
r, tan
1
y
x
.
If (x, y) lies in the second or third quadrant, then its polar coordinates are
r, tan
1
y
x
p
.
(b) Begin by eliminating fractions.
r
1
1
sin u
r(1 sin u) 1
r r sin u 1
Substitute r
x
2
y
2
and y r sin u:
x
2
y
2
y 1
Rearrange terms:
x
2
y
2
y 1
Square both sides: x
2
y
2
(y 1)
2
Simplify: x
2
y
2
y
2
2y 1
x
2
2y 1
y
1
2
(x
2
1)
As we saw in Section 4.1, the graph is an upward-opening parabola. ■
POLAR GRAPHS
The graphs of a few polar coordinate equations can be easily determined from the
appropriate definitions.
EXAMPLE 5
Graph the equations
(a) r 3* (b) u p/6.*
SOLUTION
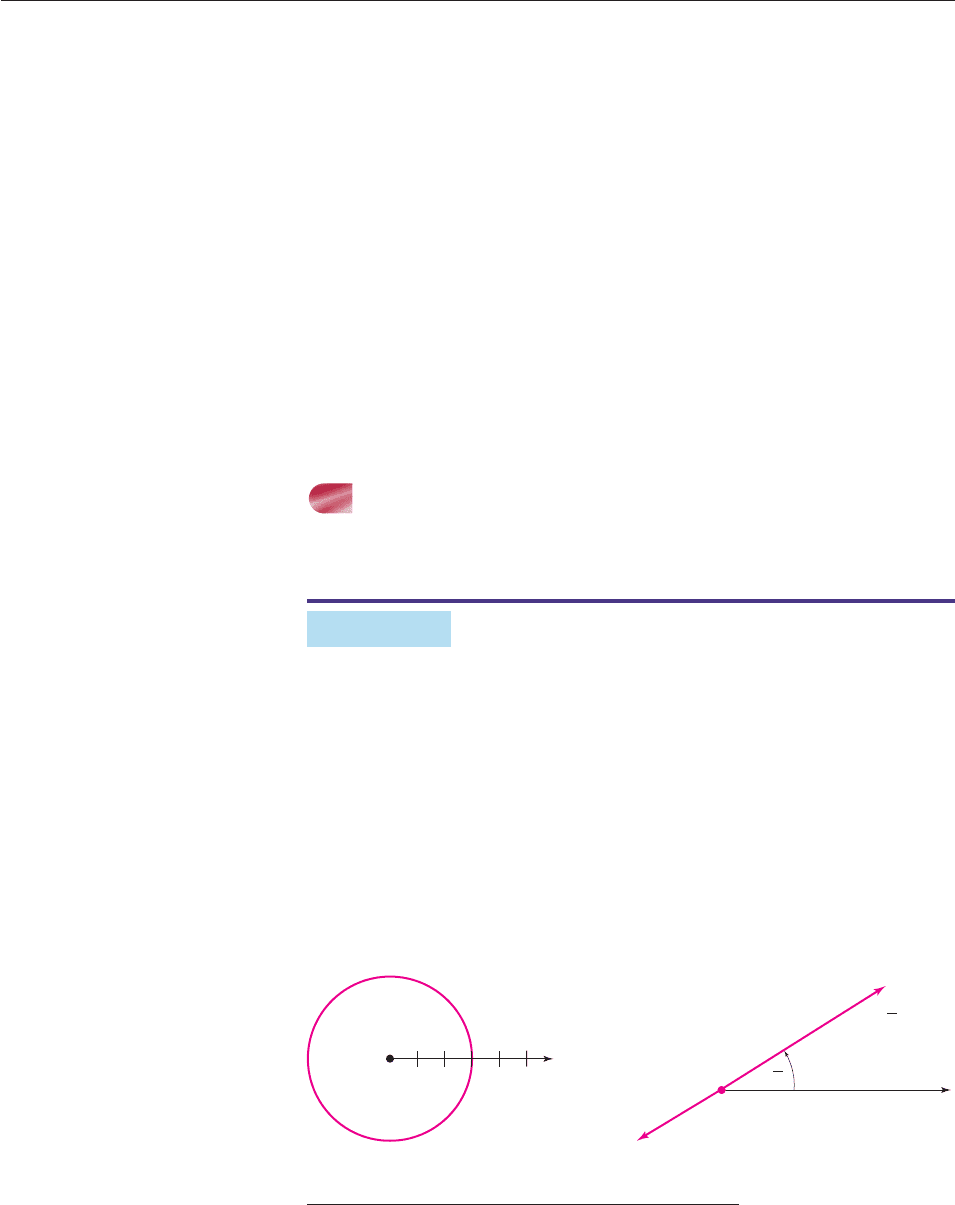
(a) The graph consists of all points (r, u) with first coordinate 3, that is, all points
whose distance from the origin is 3. So the graph is a circle with center O and
radius 3, as shown in Figure 10–85.
(b) The graph consists of all points (r, p/6). If r 0, then (r, p/6) lies on the
terminal side of an angle of p/6 radians, whose initial side is the polar axis.
If r 0, then (r, p/6) lies on the extension of this terminal side across the
origin. So the graph is the straight line in Figure 10–86. ■
Figure 10–85 Figure 10–86
Polar axis
=
θ
π
6
π
6
O
Polar axis
O
r = 3
5
4321
SECTION 10.6 Polar Coordinates 747
*Every equation is understood to involve two variables, but one may have coefficient 0, as is the case
here: r 3 0
u and u 0
r p/6. This is analogous to equations such as y 5 and
x 2 in rectangular coordinates.
Some polar graphs can be sketched by hand by using basic facts about trig-
onometric functions.
EXAMPLE 6
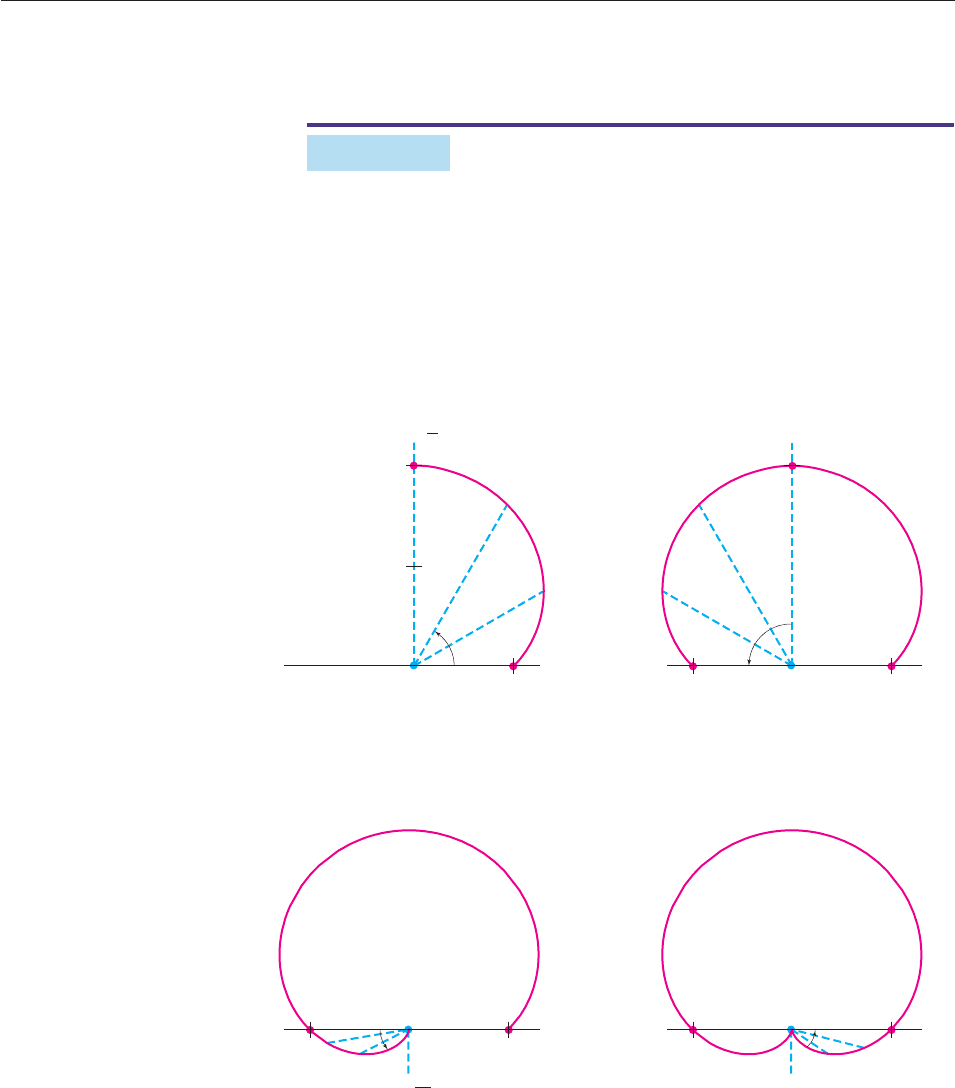
Graph r 1 sin u.
SOLUTION Remember the behavior of sin u between 0 and 2p:
Figure 10–87
As u takes values larger than 2p, sin u repeats the same pattern, and hence, so
does r 1 sin u. The same is true for negative values of u. The full graph
(called a cardioid) is at the lower right in Figure 10–87. ■
θ
θθ
θ
=
θ
=π
θ
= 2π
π
2
1
O
1
As increases from 0 to π/2, sin
increases from 0 to 1. So
r = 1 + sin increases from 1 to 2.
θθ
θ
As increases from π/2 to π, sin
decreases from 1 to 0. So
r = 1 + sin decreases from 2 to 1.
θθ
θ
As increases from π to 3π/2, sin
decreases from 0 to −1. So
r = 1 + sin decreases from 1 to 0.
θ
θ
θ
As increases from 3π/2 to 2π, sin
increases from −1 to 0. So
r = 1 + sin increases from 0 to 1.
O
1
2
1
θ
=
3π
2
2
O
11
O
11
748 CHAPTER 10 Analytic Geometry
The easiest way to graph polar equation r f (u) is to use a calculator in polar
graphing mode. A second way is to use parametric graphing mode, with the coor-
dinate converison formulas as a parameterization.
x r cos u f (u) cos u,
y r sin u f (u) sin u.
EXAMPLE 7
Graph r 2 4 cos u.
SOLUTION Polar Method: Put your calculator in polar graphing mode
and enter r 2 4 cos u in the function memory. Set the viewing window by en-
tering minimum and maximum values for x, y, and u. Since cosine has period 2p,
a complete graph can be obtained by taking 0 u 2p. You must also set the
u step (or u pitch), which determines how many values of u the calculator uses
to plot the graph. With an appropriate u step, the graph should look like
Figure 10–88.
Parametric Method: Put your calculator in parametric graphing mode. The
parametric equations for r 2 4 cos u are as follows (using t as the variable
instead of u with 0 t 2p):
x r cos t (2 4 cos t) cos t 2 cos t 4 cos
2
t
y r sin t (2 4 cos t) sin t 2 sin t 4 sin t cos t.
They also produce the graph in Figure 10–88. ■
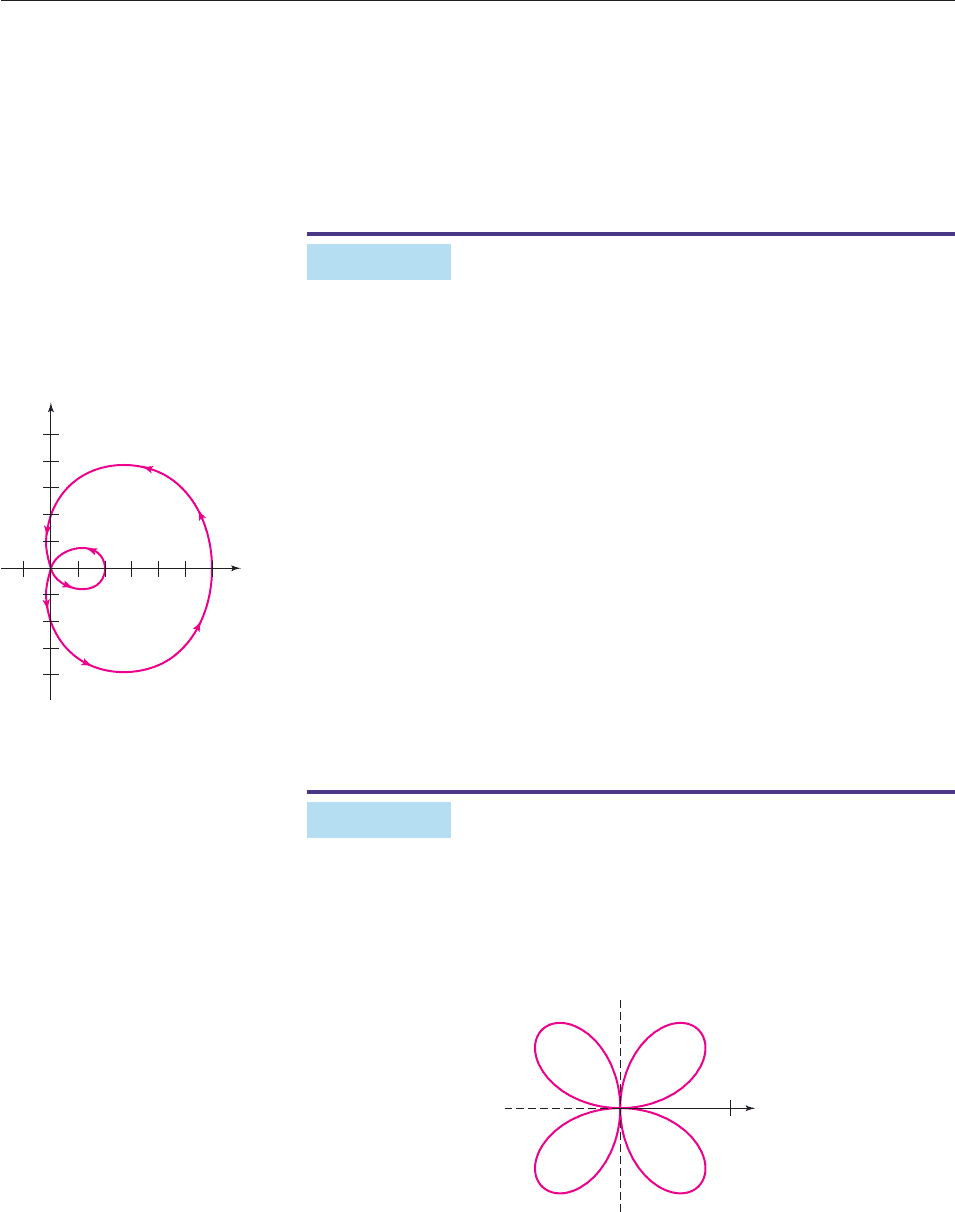
EXAMPLE 8
The graph of r sin 2u in Figure 10–89 can be obtained either by graphing
directly in polar mode or by using parametric mode and the equations
x r cos t sin 2t cos t and y r sin t sin 2t sin t (0 t 2p). ■
Figure 10–89
O
r = sin 2
θ
1
SECTION 10.6 Polar Coordinates 749
2
2
2
−2
6
y
x
Figure 10–88
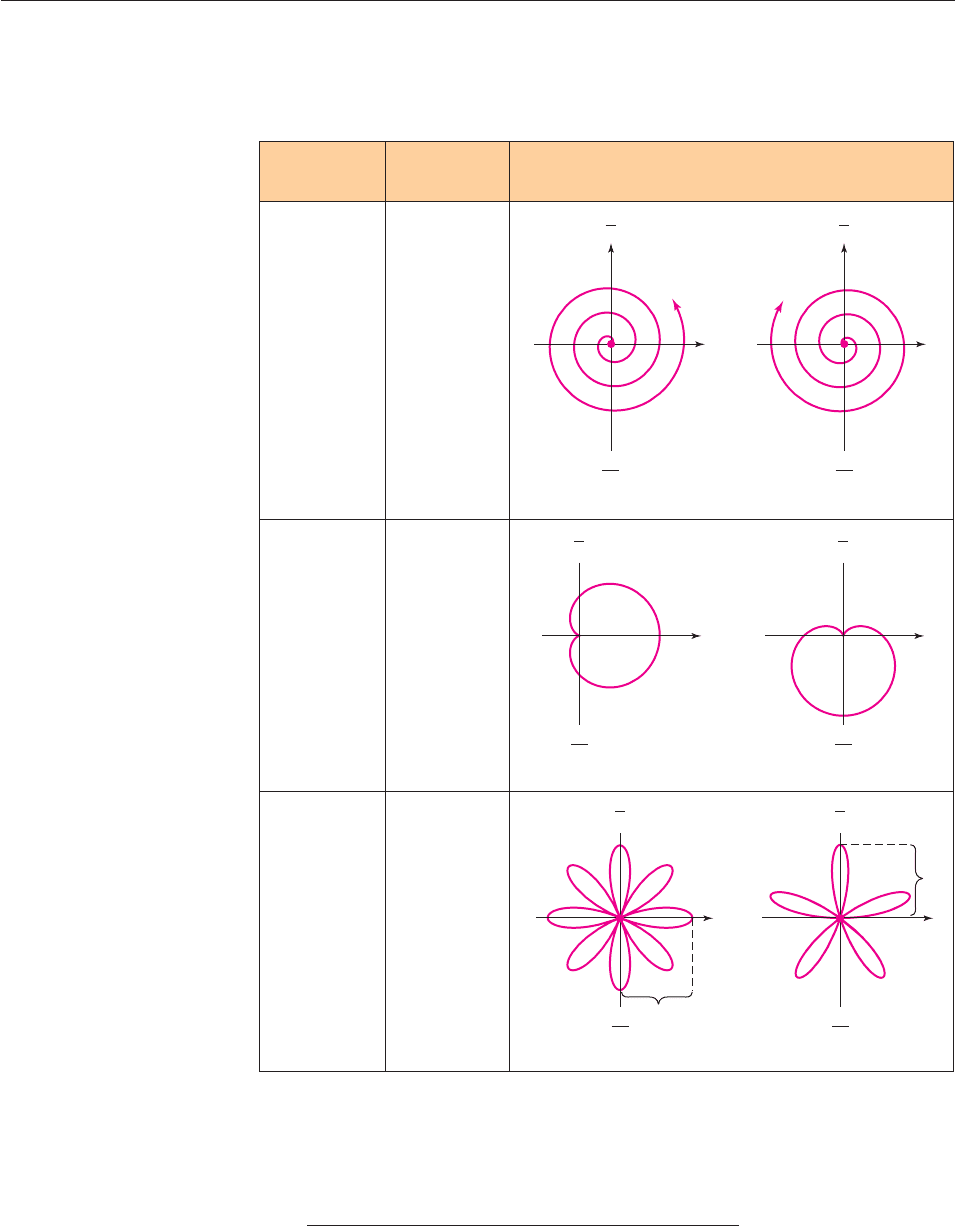
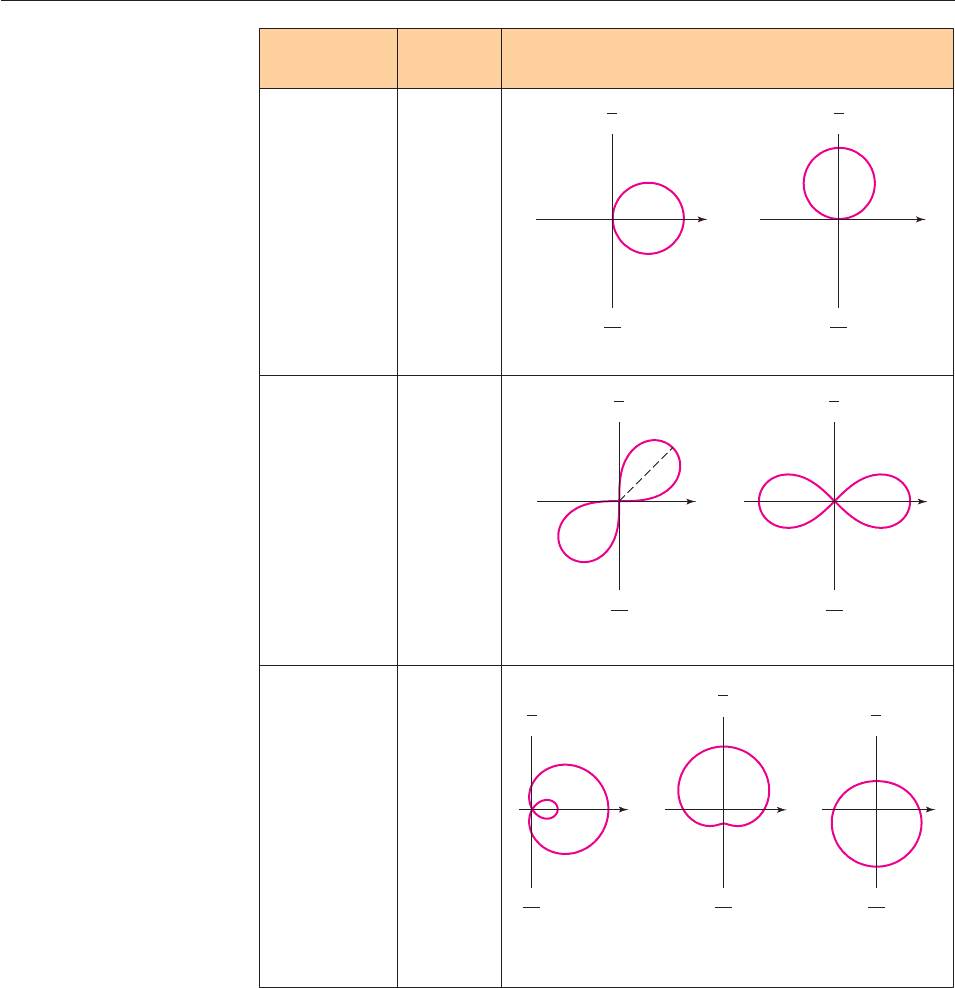
Here is a summary of commonly encountered polar graphs (in each case, a
and b are constants).
750 CHAPTER 10 Analytic Geometry
*Depending on the plus or minus sign and whether sine or cosine is involved, the basic shape of a
specific graph may differ from those shown by a rotation, reversal, or horizontal or vertical shift.
0
π
2
r = a
Equation Shape of Graph
*
Name of
Graph
≥(0)
θ
θ
θ
r = a
Archimedean
spiral
cardioid
≥(0)
θθ
r = a ≤(0)
θθ
r = a ≤(0)
θθ
π
π
3π
2
0
π
2
r = a(1 + cos )
θ
r = a(1 ± sin )
θ
r = a(1 ± cos
(There are n
petals when n
is odd and 2n
petals when n
is even.)
rose
θ
r = a sin n
θ
r = a cos n
(n ≥ 2)
)
θ
θ
r = a(1 − sin )
3π
2
π
0
π
2
3π
2
π
0
π
2
n = 4
a
3π
2
π
0
π
2
r = a sin n
θ
r = a cos n
n = 5
a
3π
2
0
π
2
π
3π
2
SECTION 10.6 Polar Coordinates 751
π
0
π
2
3π
2
π
0
π
2
a
a
3π
2
π
0
π
2
r
2
= a
2
sin 2
3π
2
π
0
π
2
r
2
= a
2
cos 2
a
a
3π
2
π
0
π
2
b < a < 2b
r = a + b sin
3π
2
π
0
π
2
a ≥ 2b
r = a − b sin
3π
2
π
0
π
2
a < b
r = a + b cos
r = a ± b sin
r = a ± b cos
(a, b > 0; a ≠ b)
3π
2
θ
r = a sin
θ
θ
r
2
=± a
2
sin 2
θ
θ
θ
θ
θ
θ
θ
r
2
=± a
2
cos 2
θ
r = a cos
θ
r = a sin
θ
r = a cos
Equation Shape of Graph
Name of
Graph
circle
lemniscate
limaçon
752 CHAPTER 10 Analytic Geometry
EXERCISES 10.6
1. What are the polar coordinates of the points P, Q, R, S, T, U,
V in the figure?
In Exercises 2–6, plot the point whose polar coordinates are
given.
2. (1, p/4) 3. (2, 3p/4) 4. (2, 2p/3)
5. (3, 5p/3) 6. (3, p/6)
In Exercises 7–12, list four other pairs of polar coordinates for
the given point, each with a different combination of signs (that
is, r 0, u 0; r 0, u 0; r 0, u 0; r 0, u 0).
7. (3, p/3) 8. (5, p) 9. (2, 2p/3)
10. (1, p/6) 11. (3
, 3p/4) 12. (3, 7p/6)
In Exercises 13–20, convert the polar coordinates to rectangu-
lar coordinates.
13. (3, p/3) 14. (2, p/4) 15. (1, 5p/6)
16. (2, 0) 17. (1.5, 5) 18. (2.2, 2.2)
19. (4, p/7) 20. (1, 1)
In Exercises 21–34, convert the rectangular coordinates to
polar coordinates.
21. (33
, 3) 22. (23
, 2) 23. (1, 1)
24. (2
, 2
) 25. (3, 33
) 26. (2
, 6
)
27. (2, 4) 28. (3, 2) 29. (5, 2.5)
30. (6.2, 3) 31. (0, 2) 32. (.5, 3.5)
33. (2, 4) 34. (5
, 10)
In Exercises 35–40, find a polar equation that is equivalent to
the given rectangular equation.
35. x
2
y
2
25 36. 4xy 1 37. x 12
38. y 4 39. y 2x 1 40. y x 2
P
Q
R
π
7π
6
S
T
U
V
1357
Polar axis
π
3
−
π
4
π
2
2π
3
In Exercises 41–52, find a rectangular equation that is equiva-
lent to the given polar equation.
41. r 3[Hint: Square both sides, then substitute.]
42. r 5
43. u p/6 {Hint: Take the tangent of both sides, then substi-
tute.]
44. u p/4
45. r sec u [Hint: Express the right side in terms of cosine.]
46. r csc u 47. r
2
tan u 48. r
2
sin u
49. r 2 sin u 50. r 3 cos u
51. r
1
4
sin u
52. r
1
6
cos u
In Exercises 53–58, sketch the graph of the equation without
using a calculator.
53. r 4 54. r 1 55. u p/3
56. u 5p/6 57. u 1 58. u 4
In Exercises 59–82, sketch the graph of the equation.
59. r u (u 0) 60. r 3u (u 0)
61. r 1 sin u 62. r 3 3 cos u
63. r 2 cos u 64. r 6 sin u
65. r cos 2u 66. r cos 3u
67. r sin 3u 68. r sin 4u
69. r
2
4 cos 2u 70. r
2
sin 2u
71. r 2 4 cos u 72. r 1 2 cos u
73. r sin u cos u 74. r 4 cos u 4 sin u
75. r sin (u/2) 76. r 4 tan u
77. r sin u tan u (cissoid)
78. r 4 2 sec u (conchoid)
79. r e
u
(logarithmic spiral)
80. r
2
1/u 81. r 1/u (u 0) 82. r
2
u
83. (a) Find a complete graph of r 1 2 sin 3u.
(b) Predict what the graph of r 1 2 sin 4u will look
like. Then check your prediction with a calculator.
(c) Predict what the graph of r 1 2 sin 5u will look
like. Then check your prediction with a calculator.
84. (a) Find a complete graph of r 1 3 sin 2u.
(b) Predict what the graph of r 1 3 sin 3u will look
like. Then check your prediction with a calculator.
(c) Predict what the graph of r 1 3 sin 4u will look
like. Then check your prediction with a calculator.
85. If a, b are nonzero constants, show that the graph of r
a sin u b cos u is a circle. [Hint: Multiply both sides by r
and convert to rectangular coordinates.]
86. Prove that the coordinate conversion formulas are valid when
r 0. [Hint: If P has coordinates (x, y) and (r, u), with r 0,
verify that the point Q with rectangular coordinates (x, y)
has polar coordinates (r, u). Since r 0, r is positive and
the conversion formulas proved in the text apply to Q. For
instance, x r cos u, which implies that x r cos u.]
87. Distance Formula for Polar Coordinates: Prove that the
distance from (r, u) to (s, b) is
r
2
s
2
2r
s cos(u
b)
[Hint: If r 0, s 0, and u b, then the triangle with ver-
tices (r, u), (s, b), (0, 0) has an angle of u b, whose sides
have lengths r and s. Use the Law of Cosines.]
SECTION 10.7 Polar Equations of Conics 753
88. Explain why the following symmetry tests for the graphs of
polar equations are valid.
(a) If replacing u by u produces an equivalent equation,
then the graph is symmetric with respect to the line
u 0 (the x-axis).
(b) If replacing u by p u produces an equivalent equa-
tion, then the graph is symmetric with respect to the line
u p/2 (the y-axis).
(c) If replacing r by r produces an equivalent equation,
then the graph is symmetric with respect to the
origin.
10.7 Polar Equations of Conics
■ Find the eccentricity of a conic section.
■ Learn the polar form for equations of conic sections.
■ Find the polar equation of a conic section.
In a rectangular coordinate system, each type of conic section has a different def-
inition. By using polar coordinates, it is possible to give a unified treatment of
conics and their equations. Before doing this, we must first introduce a concept
that will play a key role in the development.
Recall that both ellipses and hyperbolas are defined in terms of two foci and both
have two vertices that lie on the line through the foci (see pages 672–673 and
686–687). The eccentricity of an ellipse or a hyperbola is denoted e and is defined to
be the ratio
e .
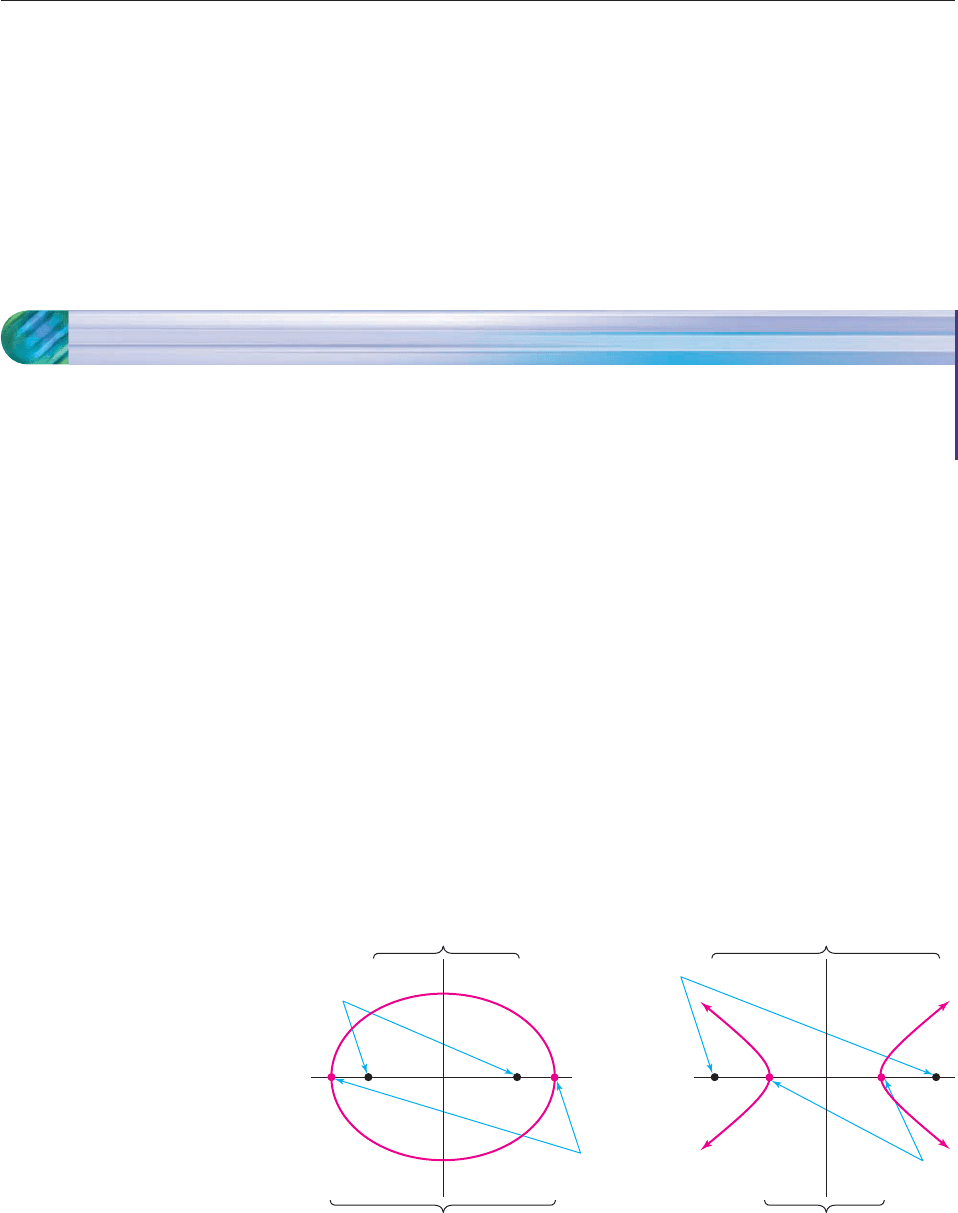
For conics centered at the origin, with foci on the x-axis, the situation is as follows.
Ellipse Hyperbola
x
a
2
2
y
b
2
2
1(a b)
x
a
2
2
y
b
2
2
1
foci: (c, 0) vertices: (a, 0) foci: (c, 0) vertices: (a, 0)
c
a
2
b
2
c
a
2
b
2
e
2
2
a
c
a
c
a
2
a
b
2
e
2
2
a
c
a
c
a
2
a
b
2
−a
−c
−aac
−c
ca
2c
2a
2c
2a
Vertices
Vertices
Foci
Foci
distance between the foci
distance between the vertices
Section Objectives

A similar analysis shows that the formulas for e are also valid for conics whose
equations are of the form
x
b
2
2
y
a
2
2
1(a b)or
y
a
2
2
x
b
2
2
1.
These formulas can be used to compute the eccentricity of any ellipse or hyper-
bola whose equation can be put in standard form.
EXAMPLE 1
Find the eccentricity of the conic with equation
(a)
y
4
2
2
x
1
2
1; (b) 4x
2
9y
2
32x 90y 253 0.
SOLUTION
(a) In this case, a
2
4 (so a 2) and b
2
21. Hence, the eccentricity is
e
a
2
a
b
2
4
2
21
2
25
5
2
2.5.
(b) In Example 8 of Section 10.1, we saw that the equation can be put into this
standard form:
(x
9
4)
2
(y
4
5)
2
1.
Hence, its graph is just the ellipse
x
9
2
y
4
2
1
shifted vertically and horizontally. Since the shifting does not change the dis-
tances between foci or vertices, both ellipses have the same eccentricity,
which can be computed by using a
2
9 and b
2
4.
e
a
2
a
b
2
9
3
4
3
5
.745. ■
Example 1 and the preceding pictures illustrate the following fact. For
ellipses, the distance between the foci (numerator of e) is less than the distance
between the vertices (denominator), so e 1. For hyperbolas, however, e 1
because the distance between the foci is greater than that between the vertices.
The eccentricity of an ellipse measures its “roundness.” An ellipse whose
eccentricity is close to 0 is almost circular (Exercise 19). The eccentricity of a
hyperbola measures how “flat” its branches are. The branches of a hyperbola with
large eccentricity look almost like parallel lines (Exercise 20).
CONICS AND POLAR EQUATIONS
The polar analogues of the standard equations of ellipses, parabolas, and hyper-
bolas are given in the following chart. The proof of these statements is given at the
end of the section. In the chart, e and d are constants, with e 0. Remember that
in a rectangular coordinate system whose positive x-axis coincides with the polar
axis, a point with polar coordinates (r, u) is on the x-axis when u 0 or p and on
the y-axis when u p/2 or 3p/2.
754 CHAPTER 10 Analytic Geometry

EXAMPLE 2
Find a complete graph of
r
1
3
e
e
cos u
when
(a) e .7 (b) e 1 (c) e 2.
SOLUTION From the first equation in the preceding chart (with d 3), we
know that the graphs are an ellipse, a parabola, and a hyperbola, respectively, as
shown in Figure 10–90. ■
Figure 10–90
−10
10
−10 10
−10
10
−10 10
e = .7
r =
2.1
1 + .7 cos
θ
−10
10
−10 10
e = 1
r =
3
1 + cos
θ
e = 2
r =
6
1 + 2 cos
(a) (b) (c)
θ
SECTION 10.7 Polar Equations of Conics 755
Polar Equations
for Conic Sections
Equation Graph
0 e 1 Ellipse with eccentricity e
One of the foci: (0, 0)
Vertices at u 0 and u p
e 1 Parabola with focus (0, 0)
Vertex at u 0 or u p; (r is not
defined for the other value of u)
e 1 Hyperbola with eccentricity e
One of the foci: (0, 0)
Vertices at u 0 and u p
0 e 1 Ellipse with eccentricity e
One of the foci: (0, 0)
Vertices at u p/2 and u 3p/2
e 1 Parabola with focus (0, 0)
Vertex at u p/2 or u 3p/2; (r is
not defined for the other value of u)
e 1 Hyperbola with eccentricity e
One of the foci: (0, 0)
Vertices at u p/2 and u 3p/2
r
1
e
e
d
cos u
or
r
1
e
e
d
cos u
r
1
e
e
d
sin u
or
r
1
e
e
d
sin u
