Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


EXAMPLE 3
Identify the conic section that is the graph of
r
4 1
2
0
0
sin u
,
and find its vertices and eccentricity.
SOLUTION First, rewrite the equation in one of the forms listed in the preced-
ing box.
r
4 1
2
0
0
sin u
1 2.
5
5 sin u
.
This is one such form, with e 2.5 and ed 5 (so d 2). Consequently, the
graph is a hyperbola with eccentricity e 2.5 whose vertices are at
u
p
2
, r
4
2
1
0
0
1
2
6
0
1
3
0
and
u
3
2
p
, r
4 1
2
0
0
(1)
2
1
0
4
1
7
0
.
EXAMPLE 4
Find a polar equation of the ellipse with (0, 0) as a focus and vertices (3, 0) and
(6, p).
SOLUTION Because of the location of the vertices, the polar equation is of the
form r ed/(1 e cos u). We first consider the equation
r
1
e
e
d
cos u
.
Since the coordinates of the vertices satisfy the equation, we must have
3
1
e
e
d
cos 0
1
e
d
e
and 6
1 e
ed
cos p
1
e
d
e
,
which imply that
3(1 e) ed and 6(1 e) ed.
20
4 10 sin
3
2
p
20
4 10 sin
p
2
20
4
1
1
4
0
sin u
756 CHAPTER 10 Analytic Geometry
Find a viewing window that shows a complete graph of this hyperbola.
GRAPHING EXPLORATION
■

Therefore,
3(1 e) 6(1 e)
3 3e 6 6e
9e 3
e 1/3.
Substituting e 1/3 in either of the original equations shows that d 12. So an
equation of the ellipse is
r
1
e
e
d
cos u
3
1
c
2
os u
.
If we had started instead with the equation r ed/(1 e cos u) and solved for
e as above, we would have obtained e 1/3, which is impossible, since
e 0.
ALTERNATE SOLUTION Verify that the vertex (3, 0) also has polar coordinates
(3, p). Similarly, (6, p) also has polar coordinates (6, 0). If you begin with the
equation r ed/(1 e cos u) and the vertices (3, p) and (6, 0) and proceed
as before to find e and d, you obtain the equation
r
3
c
1
o
2
s u
. ■
ALTERNATE DEFINITION OF CONICS
The theorem stated in the following box is sometimes used as a definition of the
conic sections because it provides a unified approach instead of the variety of
descriptions given in Sections 10.1–10.3. Its proof also provides a proof of the
statements in the box on page 755.
The basic idea is to describe every conic in terms of a straight line L (the
directrix) and a point P not on L (the focus), in much the same way that parabo-
las were defined in Section 10.3. The number e in the theorem turns out to be the
eccentricity of the conic.
1
3
12
1
1
3
cos u
SECTION 10.7 Polar Equations of Conics 757
*The distance from X to L is measured along the line through X that is perpendicular to L.
†
When e 1, the given condition is equivalent to
distance from X to P distance from X to L
which is the definition of a parabola given in Section 10.3.
Conic Section
Theorem
Let L be a straight line, P a point not on L, and e a positive constant. The
set of all points X in the plane such that
e
is a conic section with P as one of the foci.* The conic is an ellipse if
0 e 1, a parabola if e 1,
†
and a hyperbola if e 1.
distance from X to P
distance from X to L
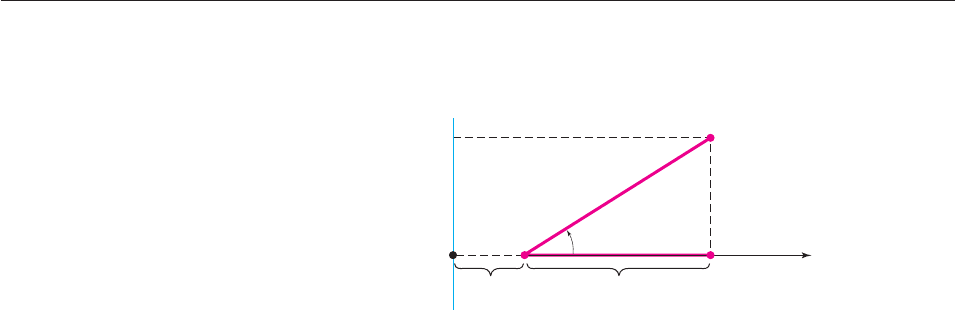
Proof Coordinatize the plane so that the pole is the point P, the polar axis is hor-
izontal, and the directrix L is a vertical line to the left of the pole, as in Figure 10–91.
Let d be the distance from P to L, and let (r, u) be the polar coordinates of X.
Figure 10–91
If X satisfies the condition
e,
then
(
*
) distance from X to P e(distance from X to L).
Figure 10–91 shows that r is the distance from P to X and that the distance from
X to L is the same as that from D to Q, namely, d s. Furthermore, cos u s/r, so
s r cos u. Consequently, equation (
*
) can be written in polar coordinates as follows.
distance from X to P e(distance from X to L)
r e(d s)
r e(d r cos u)
r er cos u ed
r(1 e cos u) ed
r
1
e
e
d
cos u
.
To show that this is actually the equation of a conic, we translate it into rect-
angular coordinates using the conversion formulas from Section 10.6.
r
2
x
2
y
2
and cos u
x
r
.
Then the polar coordinate equation becomes
x
2
y
2
x
2
y
2
1
ed
x
2
y
2
ex ed
x
2
y
2
ed ex.
Squaring both sides and rearranging terms, we have
x
2
y
2
e
2
d
2
2de
2
x e
2
x
2
(
**
) (1 e
2
)x
2
2de
2
x y
2
e
2
d
2
.
Now we consider the two possibilities e 1 and e 1.
ex
x
2
y
2
ed
1 e
x
x
2
y
2
x
x
2
y
2
distance from X to P
distance from X to L
Polar axis
(r, )
X
Q
θ
θ
r
s
d
P
D
L
758 CHAPTER 10 Analytic Geometry

Case 1: If e 1, then equation (
**
) becomes
2dx y
2
d
2
y
2
2dx d
2
(y 0)
2
2d
x
d
2
(y 0)
2
4
d
2
x
d
2
.
The box on page 707 (with k 0, p d/2, h d/2) shows that this is the
standard equation of a parabola with
vertex
d
2
, 0
, focus (0, 0), directrix x d.
Case 2: If e 1, then we can divide both sides of equation (
**
) by the nonzero
number 1 e
2
.
x
2
1
2
de
e
2
2
x
1
y
2
e
2
1
e
2
d
2
e
2
.
Next, we complete the square on the expression in parentheses by adding the square
of half of the coefficient of x to both sides of the equation and simplify the result.
x
2
1
2
de
e
2
2
x
1
d
e
2
e
2
2
1
y
2
e
2
1
e
2
d
2
e
2
1
d
e
2
e
2
2
x
1
d
e
2
e
2
2
1
y
2
e
2
x
1
d
e
2
e
2
2
1
y
2
e
2
(1
e
2
d
e
2
2
)
2
.
Dividing both sides of the last equation by e
2
d
2
/(1 e
2
)
2
produces the equation
(
***
) 1.
Now we consider the two possibilities e 1 and e 1.
Case 2A: If e 1, then 1 e
2
0 and the constants in the denominators on the
left side of equation (
***
) are positive. Therefore, equation (
***
) is of the form
(x
a
2
h)
2
(y
b
2
k)
2
1
with h de
2
/(1 e
2
), k 0, and a and b positive numbers such that
a
2
(1
e
2
d
e
2
2
)
2
and b
2
1
e
2
d
2
e
2
.
In this case, a b by Exercise 47. According to the box on page 679, this is the
standard equation of an ellipse with center (h, 0) and foci (h c, 0) and (h c, 0),
where c
2
a
2
b
2
. Its eccentricity is the number
a
c
a
c
2
2
a
2
a
2
b
2
1 b
2
a
1
2
1
1
e
2
d
2
e
2
(1
e
2
d
e
2
2
)
2
e
2
e.
y
2
1
e
2
d
2
e
2
x
1
d
e
2
e
2
2
(1
e
2
d
e
2
2
)
2
(1 e
2
)e
2
d
2
(de
2
)
2
(1 e
2
)
2
SECTION 10.7 Polar Equations of Conics 759

Case 2B: If e 1, then 1 e
2
0. Therefore,
e
2
1 (1 e
2
) 0,
so equation (
***
) may be written as
1.
This is an equation of the form
(x
a
2
h)
2
(y
b
2
k)
2
1
with a and b positive. The box on page 693 shows that it is the standard equation
of a hyperbola with foci (h c, 0) and (h c, 0), where c
2
a
2
b
2
. Exercise
48 shows that its eccentricity is e.
The preceding argument depends on coordinatizing the plane in a certain way
and taking d to be the distance from the pole to L. Similar arguments, in which d
is the distance from the pole to L and the plane is coordinatized so that L is to the
right of the pole or parallel to the polar axis, lead to the other polar equations
shown in Figure 10–92.
Figure 10–92
Analogous arguments when d 0 (using d as the distance from the pole to L)
then complete the proof. ■
Polar
axis
r =
ed
1 − e cos
θ
L
L
L
L
P
Polar
axis
P
Polar
axis
P
Polar
axis
P
r =
ed
1 − e sin
θ
r =
ed
1 + e cos
θ
r =
ed
1 + e sin
θ
y
2
e
2
e
2
d
2
1
x
1
d
e
2
e
2
2
(1
e
2
d
e
2
2
)
2
760 CHAPTER 10 Analytic Geometry
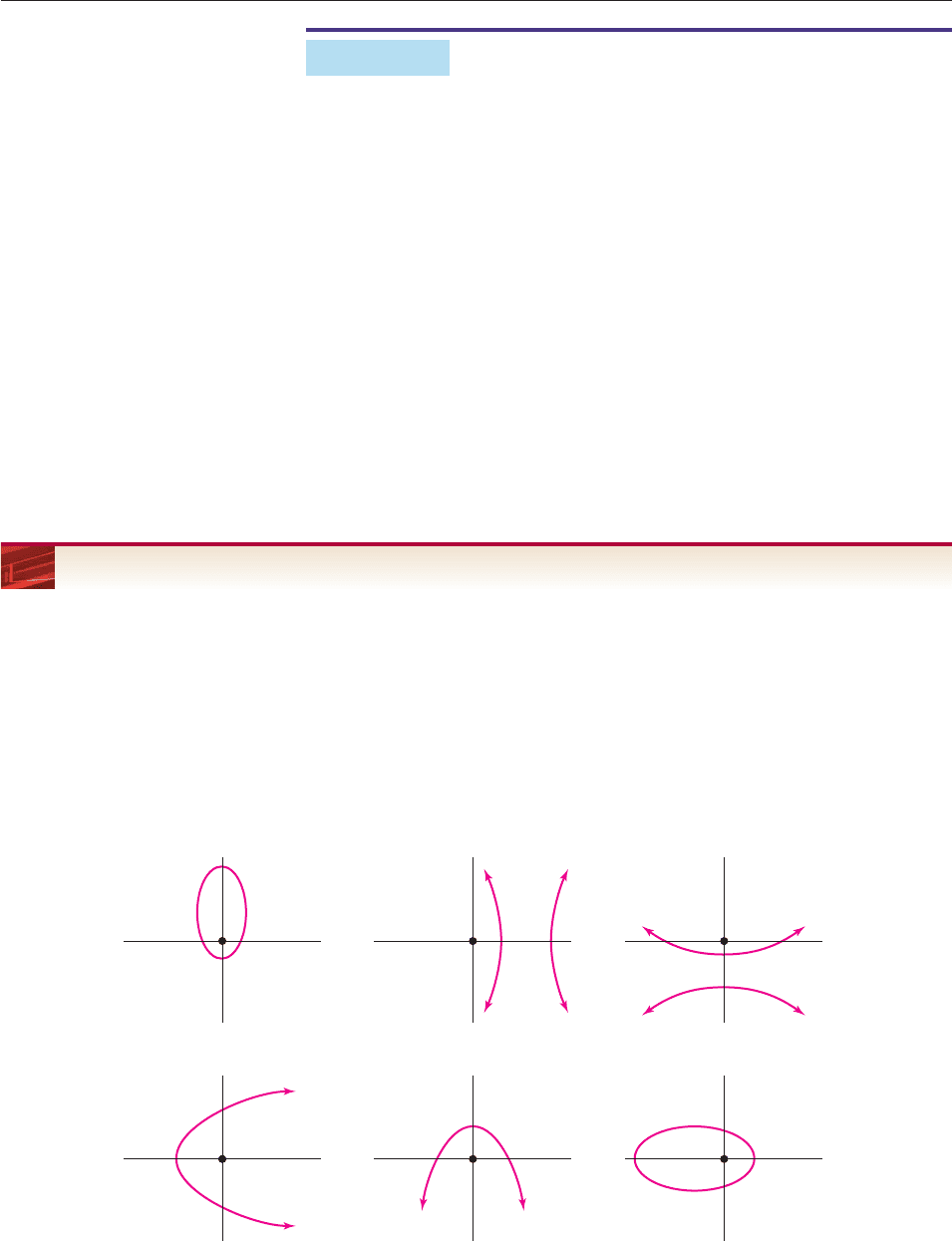
EXAMPLE 5
Find the polar equation of the hyperbola with focus at the pole, directrix
r 4 csc u,
and eccentricity 3.
SOLUTION The equation of the directrix can be written as
r
s
in
4
u
or, equivalently, r sin u 4.
With the conversion formulas for a rectangular coordinate system whose positive
x-axis coincides with the polar axis, this equation becomes y 4. So the direc-
trix is a line parallel to the polar axis and 4 units below it. Using Figure 10–92, we
see that d 4, and the equation is
r
1
e
e
d
sin u
1
1
3
2
sin u
. ■
3
4
1 3 sin u
SECTION 10.7 Polar Equations of Conics 761
EXERCISES 10.7
In Exercises 1–6, which of the graphs (a)–(f) at the bottom of
the page could possibly be the graph of the equation?
1. r
1
3
cos u
2. r
2
6
cos u
3. r
2 4
6
sin u
4. r
1
1
4
5
cos u
5. r
3 2
6
sin u
6. r
6
3
2
3
2
sin u
In Exercises 7–12, identify the conic section whose equation is
given; if it is an ellipse or hyperbola, state its eccentricity.
7. r
3
1
4
2
sin u
8. r
2
3
1
c
0
os u
9. r
3 3
8
sin u
10. r
5 1
2
0
0
sin u
11. r
6 4
2
cos u
12. r
5
2
6
cos u
(a) (b)
(d)
(c)
(f)(e)

In Exercises 13–18, find the eccentricity of the conic whose
equation is given.
13.
1
x
0
2
0
9
y
9
2
1 14.
(x
18
4)
2
(y
25
5)
2
1
15.
(x
10
6)
2
4
y
0
2
1
16. 4x
2
9y
2
24x 36y 36 0
17. 16x
2
9y
2
32x 36y 124 0
18. 4x
2
5y
2
16x 50y 71 0
19. (a) Using a square viewing window (so that circles look
like circles), graph these ellipses (on the same screen if
possible):
1
x
6
2
y
1
2
1,
1
x
6
2
y
6
2
1,
1
x
6
2
1
y
4
2
1
(b) Compute the eccentricity of each ellipse in part (a).
(c) On the basis of parts (a) and (b), how is the shape of an
ellipse related to its eccentricity?
20. (a) Graph these hyperbolas (on the same screen if possible):
y
4
2
x
1
2
1,
y
4
2
1
x
2
2
1,
y
4
2
9
x
6
2
1
(b) Compute the eccentricity of each hyperbola in part (a).
(c) On the basis of parts (a) and (b), how is the shape of a
hyperbola related to its eccentricity?
In Exercises 21–32, sketch the graph of the equation and label
the vertices.
21. r
1
8
cos u
22. r
3 2
5
sin u
23. r
2 4
4
cos u
24. r
1
5
cos u
25. r
4
1
3
0
sin u
26. r
3
1
4
2
sin u
27. r
3
1
2
5
cos u
28. r
3
3
5
2
sin u
762 CHAPTER 10 Analytic Geometry
29. r
1
3
sin u
30. r
3
1
2
0
cos u
31. r
2
1
3
0
sin u
32. r
4
1
4
5
cos u
In Exercises 33–46, find the polar equation of the conic section
that has focus (0, 0) and satisfies the given conditions.
33. Parabola; vertex (3, p)
34. Parabola; vertex (2, p/2)
35. Ellipse; vertices (2, p/2) and (8, 3p/2)
36. Ellipse; vertices (2, 0) and (4, p)
37. Hyperbola; vertices (1, 0) and (3, p)
38. Hyperbola; vertices (2, p/2) and (4, 3p/2)
39. Eccentricity 4; directrix; r 2 sec u
40. Eccentricity 2; directrix: r 4 csc u
41. Eccentricity 1; directrix: r 3 csc u
42. Eccentricity 1; directrix: r 5 sec u
43. Eccentricity 1/2; directrix: r 2 sec u
44. Eccentricity 4/5; directrix: r 3 csc u
45. Hyperbola; vertical directrix to the left of the pole; eccen-
tricity 2; (1, 2p/3) is on the graph.
46. Hyperbola; horizontal directrix above the pole; eccentricity
2; (1, 2p/3) is on the graph.
47. In Case 2A of the proof of the Conic Section Theorem, show
that a b.
48. In Case 2B of the proof of the Conic Section Theorem, show
that the hyperbola has eccentricity e.
49. A comet travels in a parabolic orbit with the sun as focus.
When the comet is 60 million miles from the sun, the line
segment from the sun to the comet makes an angle of p/3
radians with the axis of the parabolic orbit. Using the sun as
the pole and assuming the axis of the orbit lies along the
polar axis, find a polar equation for the orbit.
50. Halley’s Comet has an elliptical orbit, with eccentricity .97
and the sun as a focus. The length of the major axis of the
orbit is 3364.74 million miles. Using the sun as the pole and
assuming the major axis of the orbit is perpedicular to the
polar axis, find a polar equation for the orbit.

Chapter 10 Review
IMPORTANT CONCEPTS
Section 10.1
Circle 671
Equations of circles 671
Ellipse 672
Foci 672
Center 673
Major and minor axes 673
Equations of ellipses 674, 679
Vertical and horizontal shifts 677
Section 10.2
Hyperbola 686–687
Foci 687
Center 687
Vertices 687
Asymptotes 687
Equations of hyperbolas 687, 693
Vertical and horizontal shifts 690
Section 10.3
Parabola 700
Focus 700
Directrix 700
Vertex 700
Equations of parabolas 701, 707
Latus rectum 703
Vertical and horizontal shifts 705
Special Topics 10.3.A
Parametric equations for circles,
ellipses, hyperbolas,
and parabolas 714–715
Section 10.4
Graphs of rotated conics 718–720
Discriminant 720
Special Topics 10.4.A
Rotation equations 723
Eliminating the xy term 725
Section 10.5
Plane curve 728
Parameter 728
Parametric equations 728
Eliminating the parameter 731
Finding parameterizations 733
Projectile motion 736
Cycloid 737
Section 10.6
Polar coordinates 743
Pole 743
Polar axis 743
Polar/rectangular coordinate
conversion 744, 746
Polar graphs 748–751
Section 10.7
Eccentricity 753
Polar equations for conics 755
Focus 757
Directrix 757
CHAPTER 10 Review 763
IMPORTANT FACTS & FORMULAS
■
Equations of conic sections
Conic Section Cartesian Equation Parametric Equations
Circle x r cos t h
center (h, k)(x h)
2
(y k)
2
r
2
y r sin t k
radius r (0 t 2p)
Ellipse
center (h, k)
(x
a
2
h)
2
(y
b
2
k)
2
1
x a cos t h
axes on the lines y b sin t k
x h, y k (0 t 2p)
Hyperbola
center (h, k)
(x
a
2
h)
2
(y
b
2
k)
2
1
x
co
a
s t
h
vertices on the line
y b tan t k
y k
(0 t 2p)
Hyperbola
center (h, k)
x b tan t h
vertices on the line
(y
a
2
k)
2
(x
b
2
h)
2
1
y
co
a
s t
k
x h (0 t 2p)
(continued)

764 CHAPTER 10 Analytic Geometry
Conic Section Cartesian Equation Parametric Equations
Parabola
vertex (h, k)
(x h)
2
4p( y k)
x t
axis x h
y
(t
4p
h)
2
k
(t any real)
Parabola
vertex (h, k)(y k)
2
4p(x h)
x
(t
4p
k)
2
h
axis y k
y t
(t any real)
■
The discriminant of the equation Ax
2
Bxy Cy
2
Dx Ey F 0 (where A, B, C are not all zero)
is B
2
4AC.
If B
2
4AC 0, the graph is a circle or ellipse (or a point).
If B
2
4AC 0, the graph is a parabola (or a line or two parallel lines).
If B
2
4AC 0, the graph is a hyperbola (or two intersecting lines).
■
Rotation Equations:
x u cos u v sin u,
y u sin u v cos u.
■
To eliminate the xy term in Ax
2
Bxy Cy
2
Dx Ey F 0, rotate the axes through an angle u
such that cot 2u
A
B
C
.
■
The rectangular and polar coordinates of a point are related by
x r cos u and y r sin u ;
r
2
x
2
y
2
and tan u
y
x
.
■
If e and d are constants with e 0, then the graph of a polar equation of the form
r
1
e
e
d
cos u
or r
1
e
e
d
sin u
is an ellipse if 0 e 1, a parabola if e 1, and a hyperbola if e 1.
In Questions 1–4, find the foci and vertices of the conic, and
state whether it is an ellipse or a hyperbola.
1.
1
x
6
2
2
y
0
2
1 2.
x
9
2
1
y
6
2
1
3.
(x
7
1)
2
(y
16
3)
2
1 4. 3x
2
1 2y
2
5. Find the focus and directrix of the parabola 10y 7x
2
.
6. Find the focus and directrix of the parabola
3y
2
x 4y 4 0.
In Questions 7–20, sketch the graph of the equation. If there
are asymptotes, give their equations.
7.
x
4
2
2
y
5
2
1 8. 9x
2
25y
2
225
9.
(x
9
3)
2
(y
4
5)
2
1 10.
x
9
2
1
y
6
2
1
11.
(y
25
4)
2
(x
4
1)
2
1 12. 4x
2
9y
2
144
13. x
2
4y
2
10x 9 0
14. 9x
2
4y
2
36x 24y 36 0
15. 2y 4(x 3)
2
6 16. 3y 6(x 1)
2
9
17. x y
2
2y 2 18. y x
2
2x 3
19. x
2
y
2
6x 5 0
20. x
2
y
2
4x 6y 4 0
21. Find the center and radius of the circle whose equation is
x
2
y
2
8x 10y 33 0.
REVIEW QUESTIONS

22. Find the equation of the circle with center (2, 3) that
passes through the point (1, 7).
23. What is the center of the ellipse
4x
2
3y
2
32x 36y 124 0?
24. Find the equation of the ellipse with center at the origin, one
vertex at (0, 4), passing through (3
, 23
).
25. Find the equation of the ellipse with center at (3, 1), one ver-
tex at (1, 1), passing through (2, 1 3/2
).
26. Find the equation of the hyperbola with center at the origin,
one vertex at (0, 5), pass through (1, 35
).
27. Find the equation of the hyperbola with center at (3, 0), one
vertex at (3, 2), passing through (1, 5
).
28. Find the equation of the parabola with vertex (2, 5), axis
x 2, and passing through (3, 12).
29. Find the equation of the parabola with vertex (3/2, 1/2),
axis y 1/2, and passing through (3, 1).
30. Find the equation of the parabola with vertex (5, 2) that
passes through the points (7, 3) and (9, 6).
In Questions 31–40, find parametric equations for the conic
section and use them to sketch its graph.
31. (x 5)
2
(y 2)
2
9
32. (x 3)
2
(y 1)
2
4
33.
x
4
2
2
y
5
2
1 34. 36x
2
25y
2
900
35.
(x
9
3)
2
(y
4
5)
2
1 36.
x
9
2
1
y
6
2
1
37.
(y
25
4)
2
(x
4
1)
2
1 38. 4x
2
9y
2
144
39. x (y 4)
2
2 40. y
2
6y x 9 0
41. The arch shown in the figure has the shape of half of an
ellipse. How wide is the arch at a point 8 feet above the
ground? [Hint: Think of the arch as sitting on the x-axis,
with its center at the origin, and find its equation.]
42. A bridge, whose bottom is shaped like half an ellipse, spans
a 52-foot wide canal. The bottom of the bridge is 8 feet
above the water at a point 20 feet from the center of the
canal. Find the height of the bridge bottom above the water
at the center of the canal.
10 ft
10 ft
CHAPTER 10 Review 765
43. A parabolic satellite dish is 3 feet in diameter and 1 foot
deep at the vertex. How far from the vertex should the
receiver be placed to catch all the signals that hit the dish?
44. A satellite dish with a parabolic cross section is 6 feet in
diameter. The receiver is located on the center axis, 1 foot
from the base of the dish. How deep is the dish at its center?
In Questions 45–48, assume that the graph of the equation is a
nondegenerate conic. Use the discriminant to identify the graph.
45. 3x
2
22
xy 2y
2
12 0
46. x
2
y
2
xy 4y 0
47. 4xy 3x
2
20 0
48. 4x
2
4xy y
2
5
x 25
y 0
In Questions 49–54, find a viewing window that shows a com-
plete graph of the equation.
49. x
2
xy y
2
6 0
50. x
2
xy y
2
3y 6 0
51. x
2
xy 2 0
52. x
2
4xy y
2
5 0
53. x
2
3xy y
2
22
x 22
y 0
54. x
2
2xy y
2
42
y 0
In Questions 55–56, find the rotation equations when the x-y
axes are rotated through the given angle.
55. 60° 56. 45°
In Questions 57–58, find the angle through which the x-y axes
should be rotated to eliminate the xy term in the equation.
57. x
2
xy y
2
3y 6 0
58. x
2
4xy y
2
5 0
In Questions 59–62, find a viewing window that shows a com-
plete graph of the curve whose parametric equations are given.
59. x 8 cos t cos 8t
y 8 sin t sin 8t (0 t 2p)
60. x [64 cos(p/6)]t
y 16t
2
[64 sin(p/6)]t (0 t p)
3
1
