Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

The argument used in Example 9 also applies when the initial position of the
golf ball is k feet above the ground (for instance, if the golfer were on a platform
at a driving range). In that case, the ball begins at (0, k) instead of (0, 0), and its
position at time t is k feet higher than before, so its coordinates are
x (140 cos 31°)t and y (140 sin 31°)t 16t
2
k.
Then replacing 140 with v and 31° with u in Example 9 leads to this conclusion.
EXAMPLE 10
A batter hits a ball that is 3 feet above the ground. It leaves the bat at an angle of
26° with the horizontal and is headed toward a 25-foot high fence that is 400 feet
away. Will the ball go over the fence if its initial velocity is
(a) 138 feet per second? (b) 135.5 feet per second?
SOLUTION
(a) According to the preceding box (with v 138, u 26°, and k 3), the path
of the ball is given by the parametric equations
x (138 cos 26°)t and y (138 sin 26°)t 16t
2
3.
The graph of the ball’s path in Figure 10–73 was made with the grid-on fea-
ture (in the TI FORMAT menu). Vertical tick marks are 25 units apart and it
is easy to see that when the x-coordinate of the ball is 400, its y-coordinate is
larger than 25. So the ball goes over the fence.
(b) In this case, the ball’s path is given by
x (135.5 cos 26°)t and y (135.5 sin 26°)t 16t
2
3.
Our final example is a curve that has several interesting applications.
736 CHAPTER 10 Analytic Geometry
Projectile
Motion
When a projectile is fired from the position (0, k) on the positive y-axis at
an angle u with the horizontal, in the direction of the positive x-axis, with
initial velocity v feet per second, with negligible air resistance, then its po-
sition at time t seconds is given by the parametric equations
x (v cos u)t and y (v sin u)t 16t
2
k.
0
0 600
75
Figure 10–73
Find the graph of the ball’s path, using degree mode and the viewing window of Fig-
ure 10–73 (with 0 t 4 and t-step .1). If the graph is hard to read, try one or
more of the following:
1. Use the trace feature.
2. Change the t-step to .01 and regraph.
3. Use the table feature with D Tbl set very small.
Does the ball clear the wall?
GRAPHING EXPLORATION
■
EXAMPLE 11
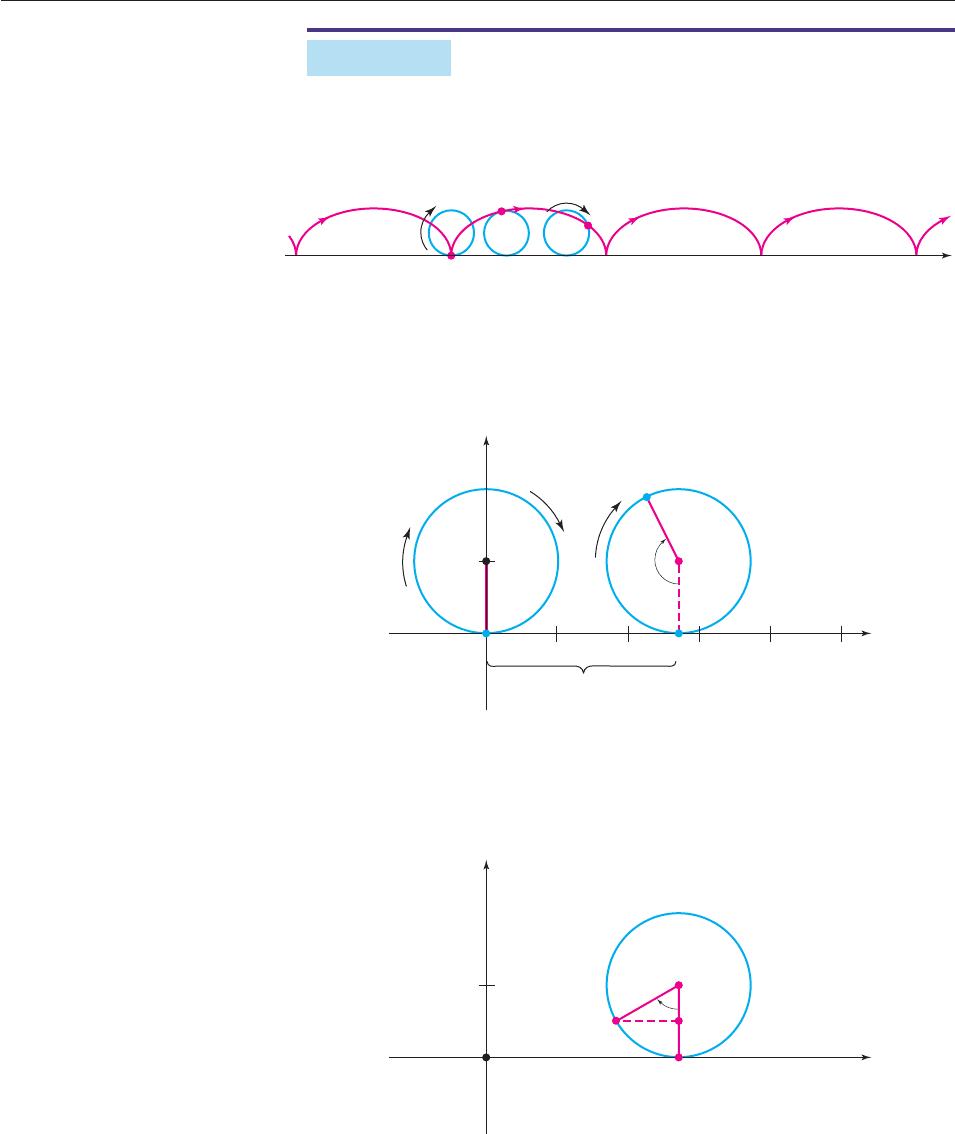
Choose a point P on a circle of radius 3, and find a parametric description of the
curve that is traced out by P as the circle rolls along the x-axis, as shown in Fig-
ure 10–74.
Figure 10–74
SOLUTION This curve is called a cycloid. Begin with P at the origin and the
center C of the circle at (0, 3). As the circle rolls along the x-axis, the line segment
CP moves from vertical through an angle of t radians, as shown in Figure 10–75.
Figure 10–75
The distance from point T to the origin is the length of arc of the circle from T to
P. As shown on page 435, this arc has length 3t. Therefore the center C has coor-
dinates (3t, 3). When 0 t p/2, the situation looks like Figure 10–76.
Figure 10–76
Right triangle PQC shows that
sin t
P
3
Q
or, equivalently, PQ 3 sin t
3
3
O
T
P
Q
(x, y)
C
t
x
y
3
36912
6
P
T
P
C
C
t
x
y
3t
P
P
P
x
SECTION 10.5 Plane Curves and Parametric Equations 737

and
cos t
C
3
Q
or, equivalently, CQ 3 cos t.
In Figure 10–76, P has coordinates (x, y) and we have
x OT PQ 3t 3 sin t 3(t sin t),
y CT CQ 3 3 cos t 3(1 cos t).
A similar analysis for other values of t (Exercises 65–67) shows that these equa-
tions are valid for every t. Therefore, the parametric equations of this cycloid are
x 3(t sin t) and y 3(1 cos t)(t any real number). ■
If a cycloid is traced out by a circle of radius r, then the argument given in
Example 11, with r in place of 3, shows that the parametric equations of the
cycloid are
x r(t sin t) and y r (1 cos t)(t any real number).
Cycloids have a number of interesting applications. For example, among all
the possible paths joining points P and Q
in Figure 10–77, an arch of an inverted
cycloid (shown in red) is the curve along which a particle (subject only to gravity)
will slide from P to Q in the shortest possible time. This fact was first proved by
J. Bernoulli in 1696.
Figure 10–77 Figure 10–78
The Dutch physicist Christiaan Huygens (who invented the pendulum clock)
proved that a particle takes the same time to slide to the bottom point Q of an
inverted cycloid arch (as in Figure 10–78) from any point P on the curve.
P
P
P
P
P
Q
P
Cycloid
Q
738 CHAPTER 10 Analytic Geometry
EXERCISES 10.5
In Exercises 1–18, find a viewing window that shows a com-
plete graph of the curve.
1. x t
2
4, y t/2, 2 t 3
2. x 3t
2
, y 2 5t,0 t 2
3. x 2t, y t
2
1, 1 t 2
4. x t 1, y
t
t
1
1
, t 1
5. x cos 4t, y cos 3t,0 t p
6. x sin 4t, y sin 3t,0 t 2p
7. x cos 3t t, y cos 4t t, p t p
8. x 3 sin t, y ln t,0 t 4p
9. x 4 sin 2t 9, y 6 cos t 8, 0 t 2p
10. x t
3
3t 8, y 3t
2
15, 4 t 4
11. x 6 cos t 12 cos
2
t, y 8 sin t 8 sin t cos t,
0 t 2p
12. x 12 cos t, y 12 sin 2t,0 t 2p

SECTION 10.5 Plane Curves and Parametric Equations 739
13. x 6 cos t 5 cos 3t, y 6 sin t 5 sin 3t,
0 t 2p
14. x 3t
2
10, y 4t
3
, any real number t
15. x 12 cos 3t cos t 6, y 12 cos 3t sin t 7,
0 t 2p
16. x 2 cos 3t 6, y 2 cos 3t sin t 7, 0 t 2p
17. x t sin t, y t cos t,0 t 8p
18. x 9 sin t, y 9t cos t,0 t 20
In Exercises 19–30, the given curve is part of the graph of an
equation in x and y. Find the equation by eliminating the
parameter.
19. x t 3, y 2t 1, t 0
20. x t 5, y t
, t 0
21. x 2 t
2
, y 1 2t
2
, any real number t
22. x t
2
1, y t
2
1, any real number t
23. x t
3
3t
2
2t, y t 1, any real number t
24. x 8t
3
4t
2
3, y 2t 4, any real number t
25. x t
, y t
4
1, t 0
26. x t
2
t 1, y t 1
, t 1
27. x e
t
, y t, any real number t
28. x 2e
t
, y 1 e
t
, t 0
29. x 3 cos t, y 3 sin t,0 t 2p
30. x 4 sin 2t, y 2 cos 2t,0 t 2p
In Exercises 31 and 32, sketch the graphs of the given curves
and compare them. Do they differ and if so, how?
31. (a) x 4 6t, y 7 12t,0 t 1
(b) x 2 6t, y 5 12t,0 t 1
32. (a) x t, y t
2
(b) x t
, y t
(c) x e
t
, y e
2t
In Exercises 33–42, use the information given in Special Topics
10.3.A and summarized in the endpapers at the beginning of this
book to find a parameterization of the conic section whose rec-
tangular equation is given. Confirm your answer by graphing.
33. circle with center (7, 4) and radius 6
34. circle with center (9, 12) and radius 5
35. x
2
y
2
4x 4y 1 0[Hint: Example 13 in Sec-
tion 1.3.]
36. x
2
y
2
4x 6y 9 0
37.
2
x
5
2
1
y
8
2
1 38.
(x
10
2)
2
(y
20
5)
2
1
39.
x
9
2
1
y
5
2
1 40.
1
y
2
2
x
8
2
1
41.
(y
36
2)
2
(x
24
5)
2
1 42.
(x
25
5)
2
(y
50
3)
2
1
43. (a) What is the slope of the line through (a, b) and (c, d )?
(b) Use the slope from part (a) and the point (a, b) to write
the equation of the line. Do not simplify.
(c) Show that the curve with parametric equations
x a (c a)t and y b (d b)t
(t any real number)
is the line through (a, b) and (c, d ). [Hint: Solve both
equations for t, and set the results equal to each other;
compare with the equation in part (b).]
44. Find parametric equations whose graph is the line segment
joining the points (a, b) and (c, d ). [Hint: Adjust the range
of t values in Exercise 43(c).]
In Exercises 45–47, use Exercise 44 to find a parameterization
of the line segment joining the two points. Confirm your an-
swer by graphing.
45. (6, 12) and (12, 10) 46. (14, 5) and (5, 14)
47. (18, 4) and (16, 14)
48. (a) Find a parameterization of the line segment joining
(5, 3) and (7, 4), as in Exercises 45–47.
(b) Explain why another parameterization of this line seg-
ment is given by
x 5 12 sin t and
y 3 7 sin t (0 t p/2).
(c) Use the trace feature to verify that the segment is traced
out twice when the t-range in part (b) is changed to
0 t p (use t-step p/20). Explain why.
(d) What happens when 0 t 2p?
49. (a) Graph the curve given by
x sin kt and y cos t (0 t 2p)
when k 1, 2, 3, and 4. Use the window with
1.5 x 1.5 and 1.5 y 1.5
and t-step p/30.
(b) Without graphing, predict the shape of the graph
when k 5 and k 6. Then verify your predictions
graphically.
50. (a) Graph the curve given by
x 3 sin 2t and y 2 cos kt (0 t 2p)
when k 1, 2, 3, 4. Use the window with 3.5 x
3.5 and 2.5 y 2.5 and t-step p/30.
(b) Predict the shape of the graph when k 5, 6, 7, 8. Ver-
ify your predictions graphically.
51. Let a be a constant. Then the curve given by
x 2a cot t and y 2a sin
2
t (0 t p)
is called a witch of Agnesi. Example 5 is the case when
a
1
2
. On the same screen, graph this curve when
(a) a 1 (b) a 2 (c) a 2.5 (d) a 4
(e) Without graphing, describe the witch of Agnesi when
a 3.

740 CHAPTER 10 Analytic Geometry
52. Find a rectangular equation for the witch of Agnesi by elimi-
nating the parameter. [See Example 5 and Exercise 51.]
In Exercises 53–55, locate all local maxima and minima (other
than endpoints) of the curve.
53. x 4t 6, y 3t
2
2, 10 t 10
54. x t
3
sin t 4, y cos t, 1.5 t 2
55. x 4t
3
t 4, y 3t
2
5, 2 t 2
56. Show that the ball’s path in Example 9 is a parabola by
eliminating the parameter in the parametric equations
x (140 cos 31°)t and y (140 sin 31°)t 16t
2
.
[Hint: Solve the first equation for t, and substitute the result
in the second equation.]
In Exercises 57–64, use a calculator in degree mode and as-
sume that air resistance is negligible.
57. A skeet is fired from the ground with an initial velocity of
110 feet per second at an angle of 28°.
(a) Graph the skeet’s path.
(b) How long is the skeet in the air?
(c) How high does it go?
58. A ball is thrown from a height of 5 feet above the ground
with an initial velocity of 60 feet per second at an angle of
50° with the horizontal.
(a) Graph the ball’s path.
(b) When and where does the ball hit ground?
59. A medieval bowman shoots an arrow which leaves the bow
4 feet above the ground with an initial velocity of 88 feet
per second at an angle of 48° with the horizontal.
(a) Graph the arrow’s path.
(b) Will the arrow go over the 40-foot-high castle wall that
is 200 feet from the archer?
60. A golfer at a driving range stands on a platform 2 feet above
the ground and hits the ball with an initial velocity of 120
feet per second at an angle of 39° with the horizontal. There
is a 32-foot-high fence 400 feet away. Will the ball fall
short, hit the fence, or go over it?
61. A golf ball is hit off the tee at an angle of 30° and lands 300
feet away. What was its initial velocity? [Hint: The ball
lands when x 300 and y 0. Use this fact and the para-
metric equations for the ball’s path to find two equations in
the variables t and v. Solve for v.]
62. A football kicked from the ground has an initial velocity of
75 feet per second.
(a) Set up the parametric equations that describe the ball’s
path. Experiment graphically with different angles to
find the smallest angle (within one degree) needed so
that the ball travels at least 150 feet.
(b) Use algebra and trigonometry to find the angle needed
for the ball to travel exactly 150 feet. [Hint: The ball
lands when x 150 and y 0. Use this fact and the
parametric equations for the ball’s path to find two equa-
tions in the variables t and u. Solve the “x equation” for
t, and substitute this result in the other one; then solve
for u. The double-angle identity may be helpful for put-
ting this equation in a form that is easy to solve.]
63. A golf ball is hit off the ground at an angle of u degrees with
an initial velocity of 100 feet per second.
(a) Graph the path of the ball when u 20°, u 40°,
u 60°, and u 80°.
(b) For what angle in part (a) does the ball land farthest
from where it started?
(c) Experiment with different angles, as in parts (a) and (b),
and make a conjecture as to which angle results in the
ball landing farthest from its starting point.
64. A golf ball is hit off the ground at an angle of u degrees with
an initial velocity of 100 feet per second.
(a) Graph the path of the ball when u 30° and when
u 60°. In which case does the ball land farthest away?
(b) Do part (a) when u 25° and u 65°.
(c) Experiment further, and make a conjecture as to the
results when the sum of the two angles is 90°.
(d) Prove your conjecture algebraically. [Hint: Find the
value of t at which a ball hit at angle u hits the ground
(which occurs when y 0); this value of t will be an ex-
pression involving u. Find the corresponding value of x
(which is the distance of the ball from the starting
point). Then do the same for an angle of 90° u and
use the cofunction identities (in degrees) to show that
you get the same value of x.]
In Exercises 65–67, complete the derivation of the parametric
equations of the cycloid in Example 11.
65. (a) If p/2 t p, verify that angle u in the figure has
measure t p/2 and that
x OT CQ 3t 3 cos
t
p
2
,
y CT PQ 3 3 sin
t
p
2
.
(b) Use the addition and subtraction identities for sine and
cosine to show that in this case,
x 3(t sin t) and y 3(1 cos t).
θ
y
3t
3
(x, y)
3
T
O
Q
C
t
P
x
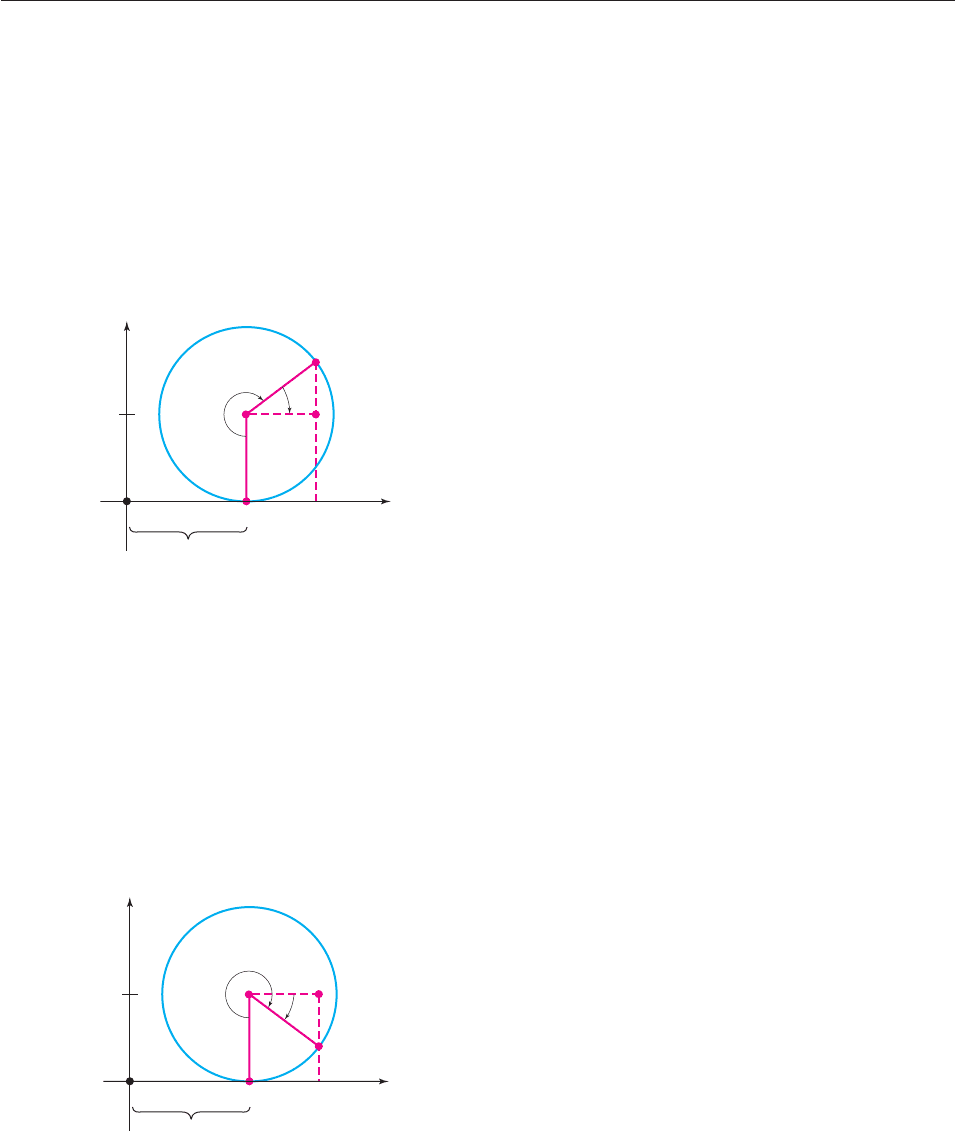
SECTION 10.5 Plane Curves and Parametric Equations 741
66. (a) If p t 3p/2, verify that angle u in the figure meas-
ures 3p/2 t and that
x OT CQ 3t 3 cos
3
2
p
t
,
y CT PQ 3 3 sin
3
2
p
t
.
(b) Use the addition and subtraction identities for sine and
cosine to show that in this case
x 3(t sin t) and y 3(1 cos t).
67. (a) If 3p/2 t 2p, verify that angle u in the figure has
measure t 3p/2 and that
x OT CQ 3t 3 cos
t
3
2
p
,
y CT PQ 3 3 sin
y
3
2
p
.
(b) Use the addition and subtraction identities for sine and
cosine to show that in this case
x 3(t sin t) and y 3(1 cos t).
THINKERS
68. A particle moves on the horizontal line y 3. Its x-
coordinate at time t seconds is given by
x 2t
3
13t
2
23t 8.
θ
y
3t
(x, y)
3
3
T
O
Q
t
C
P
x
θ
y
3t
3
(x, y)
3
T
O
Q
t
C
P
x
This exercise explores the motion of the particle.
(a) Graph the path of the particle in the viewing window
with 10 x 10, 2 y 4, 0 t 4.3, and
t step .05. Note that the calculator seems to pause
before completing the graph.
(b) Use trace (starting with t 0) and watch the path of the
particle as you press the right arrow key at regular
intervals. How many times does it change direction?
When does it appear to be moving the fastest?
(c) At what times t does the particle change direction?
What are its x-coordinates at these times?
69. Set your calculator for radian mode and for simultaneous
graphing mode [check your instruction manual for how to
do this]. Particles A, B, and C are moving in the plane, with
their positions at time t seconds given by:
A: x 8 cos t and y 5 sin t,
B: x 3t and y 5t,
C: x 3t and y 4t.
(a) Graph the paths of A and B in the window with
0 x 12, 0 y 6, and 0 t 2. The paths inter-
sect, but do the particles actually collide? That is, are
they at the same point at the same time? [For slow
motion, choose a very small t step, such as .01.]
(b) Set t step .05 and use trace to estimate the time at
which A and B are closest to each other.
(c) Graph the paths of A and C and determine geometri-
cally [as in part (b)] whether they collide. Approxi-
mately when are they closest?
(d) Confirm your answers in part (c) as follows. Explain
why the distance between particles A and C at time t is
given by
d
(8 cos
t 3t)
2
(5
sin t
4t)
2
.
A and C will collide if d 0 at some time. Using func-
tion graphing mode, graph this distance function when
0 t 2, and using zoom-in if necessary, show that d
is always positive. Find the value of t for which d is
smallest.
70. Let P be a point at distance k from the center of a circle of
radius r. As the circle rolls along the x-axis, P traces out a
curve called a trochoid. [When k r, it might help to think
of the circle as a bicycle wheel and P as a point on one of the
spokes.]
(a) Assume that P is on the y-axis as close as possible to the
x-axis when t 0, and show that the parametric equa-
tions of the trochoid are
x rt k sin t and y r k cos t.
Note that when k r, these are the equations of a cycloid.
(b) Sketch the graph of the trochoid with r 3 and
k 2.
(c) Sketch the graph of the trochoid with r 3 and k 4.
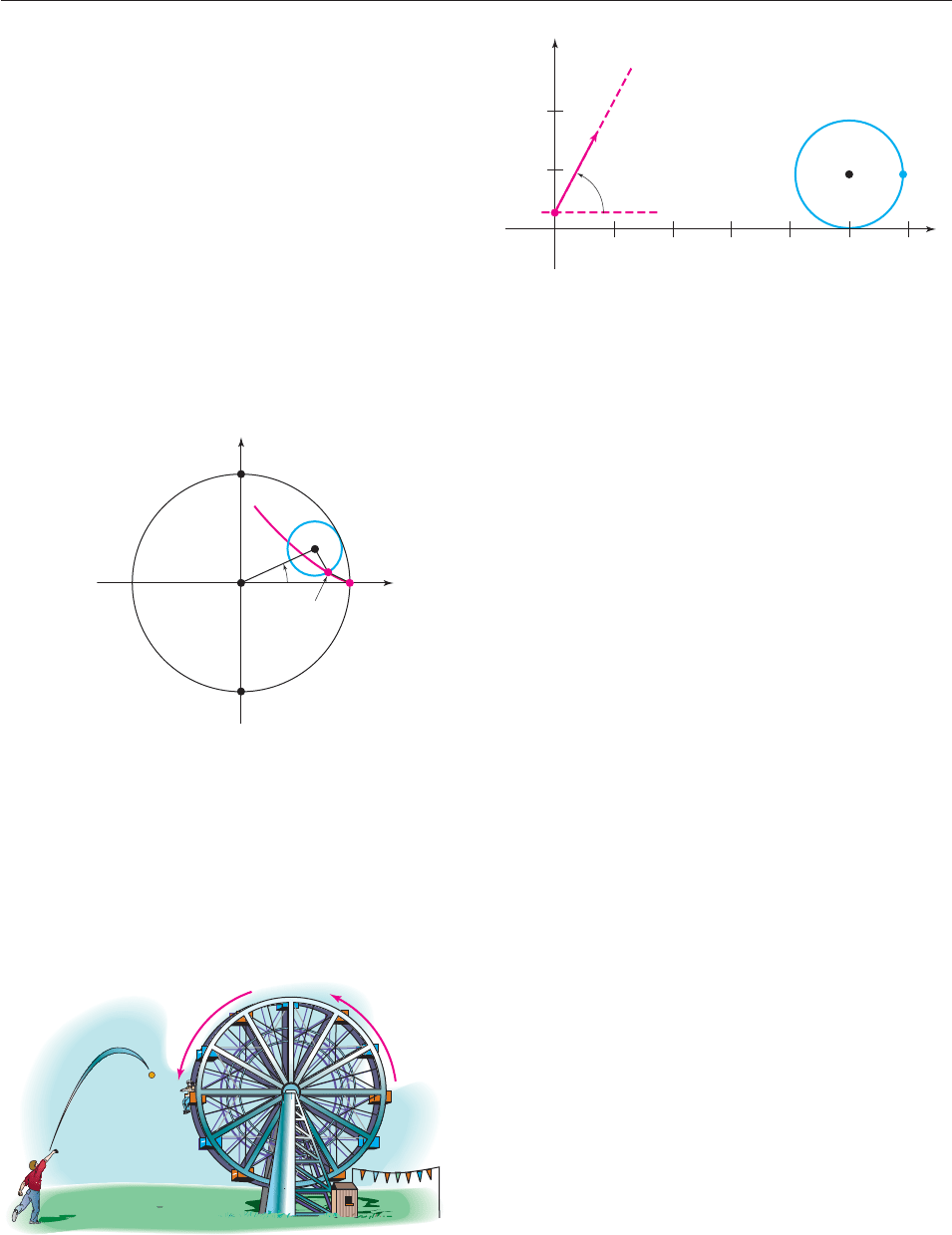
742 CHAPTER 10 Analytic Geometry
71. A circle of radius b rolls along the inside of a larger circle of
radius a. The curve traced out by a fixed point P on the
smaller circle is called a hypocycloid.
(a) Assume that the larger circle has center at the origin and
that the smaller circle starts with P located at (a, 0). Use
the figure to show that the parametric equations of the
hypocycloid are
x (a b) cos t b cos
a
b
b
t
,
y (a b) sin t b sin
a
b
b
t
.
(b) Sketch the graph of the hypocycloid with a 5, b 1,
and 0 t 2p.
(c) Sketch the graph of the hypocycloid with a 5, b 2,
and 0 t 4p.
72. Jill is on a ferris wheel of radius 20 feet whose bottom just
grazes the ground. The wheel is rotating counterclockwise
at the rate of .7 radians per second. Jack is standing 100 feet
from the bottom of the ferris wheel. When Jill is at point P,
he throws a ball toward the wheel (see the figure). The ball
leaves Jack’s hand 5 feet above the ground with an initial
velocity of 62 feet/second at an angle of 1.2 radians with
the horizontal. Will Jill be able to catch the ball? Follow the
steps to answer the question.
P
y
x
−a
−a
a
a
t
O
C
b
P
(a) Imagine that Jack is at the origin and the bottom of the
ferris wheel is at (100, 0). Then the ball leaves his hand
from the point (0, 5), and the wheel is a circle with cen-
ter (100, 20) and radius 20 (see the figure). Therefore,
the wheel is the graph of the equation
(x 100)
2
(y 20)
2
20
2
.
Show that Jill’s movement around the wheel is given by
the parametric equations
x 20 cos(.7t) 100,
y 20 sin(.7t) 20
by verifying that these equations give a parameteriza-
tion of the circle [as in Example 8].
(b) Find the parametric equations that describe the position
of the ball at time t.
(c) Set your calculator for parametric mode, radian mode,
and simultaneous graphing mode [check your instruc-
tion manual for how to do this]. Using a square viewing
window with 0 x 130, 0 t 9, and t step .1 to
graph both sets of parametric equations (Jill’s motion
and the ball’s) simultaneously. [For slow motion, make
the t step smaller.] Assuming that Jill can reach 2 feet in
any direction, can she catch the ball? If not, use the
trace to estimate the time at which Jill is closest to the
ball.
(d) Experiment by changing the angle or initial velocity (or
both) of the ball to find values that will allow Jill to
catch the ball.
x
y
20
100
1.2
5
20
40
P
SECTION 10.6 Polar Coordinates 743
10.6 Polar Coordinates
■ Convert from rectangular to polar coordinates and vice versa.
■ Graph polar coordinate equations.
In the past, we used a rectangular coordinate system in the plane, based on two
perpendicular coordinate axes. Now we introduce another coordinate system for
the plane, based on angles.
Choose a point O in the plane (called the origin or pole) and a half-line
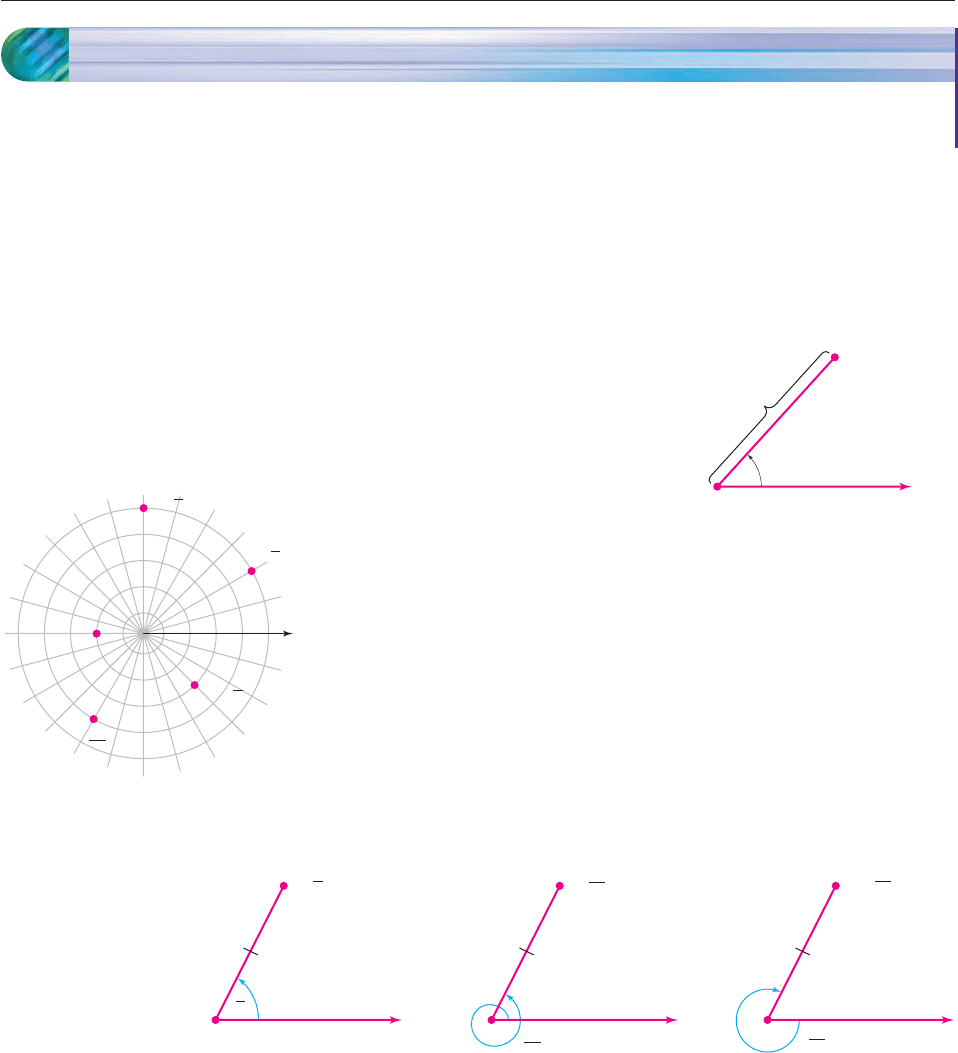
extending from O (called the polar axis). As shown in Figure 10–79, a point P is
given polar coordinates (r, u), where
r Distance from P to O
u Angle with polar axis as initial
side and OP as terminal side.
We shall usually measure the angle u in radians; it may be either positive
or negative, depending on whether it is generated by a clockwise or counter-
clockwise rotation. Some typical points are shown in Figure 10–80, which also
illustrates the “circular grid” that a polar coordinate system imposes on the
plane.
The polar coordinates of a point P are not unique. The angle u may be
replaced by any angle that has the same terminal side as u, such as u 2p. For
instance, the coordinates (2, p/3), (2, 7p/3), and (2, 5p/3) all represent the
same point, as shown in Figure 10–81.
Figure 10–81
We shall consider the coordinates of the origin to be (0, u), where u is any
angle.
Negative values for the first coordinate will be allowed according to this con-
vention: For each positive r, the point (r, u) lies on the straight line containing
the terminal side of u, at distance r from the origin, on the opposite side of the ori-
gin from the point (r, u), as shown in Figure 10–82 on the next page.
O
2,
π
3
)(
π
3
O
2,
7π
3
)(
7π
3
2,
–
5π
3
)(
–
5π
3
O
Section Objectives
Polar
axis
(r, )
Origin
θ
θ
r
P
O
Figure 10–79
Polar axis
(2, π)
5,
π
2
)(
5,
π
6
)(
3, −
π
4
)
(
4,
4π
3
)(
Figure 10–80

Figure 10–82
It is sometimes convenient to use both a rectangular and a polar coordinate
system in the plane, with the polar axis coinciding with the positive x-axis. Then
the y-axis is the polar line u p/2. Suppose P has rectangular coordinates (x, y)
and polar coordinates (r, u), with r 0, as in Figure 10–83.
Figure 10–83
Since r is the distance from (x, y) to (0, 0), the distance formula shows that
r x
2
y
2
, and hence, r
2
x
2
y
2
. The point-in-the-plane description of the
trigonometric functions shows that
cos u
x
r
, sin u
y
r
, tan u
y
x
.
Solving the first two equations for x and y, we obtain the relationship between
polar and rectangular coordinates.*
Polar axis
x-axis
y
-axis
(x, y)
(r, )
P
= 0
θ
θ
=
θ
θ
r
π
2
O
2,
π
4
)(
π
2
–2,
π
4
)(
π
4
O
O
–3,
7π
6
)(
7π
6
3,
7π
6
)(
2.5,
−
)(
π
2
−
−2.5,
)(
π
2
−
744 CHAPTER 10 Analytic Geometry
*The conclusions in the next box are also true when r 0 (Exercise 86).
Coordinate Conversion
Formulas
If a point has polar coordinates (r, u), then its rectangular coordinates (x, y) are
x r cos u and y r sin u.
If a point has rectangular coordinates (x, y), with x 0, then its polar co-
ordinates (r, u) satisfy
r
2
x
2
y
2
and tan u
y
x
.
EXAMPLE 1
Convert each of the following points in polar coordinates to rectangular coordinates.
(a) (2, p/6) (b) (3, 4)
SOLUTION
(a) Apply the first set of equations in the box with r 2 and u p/6.
x 2 cos
p
6
2
2
3
3
and y 2 sin
p
6
2
1
2
1
So the rectangular coordinates are (3
, 1).
(b) The point with polar coordinates (3, 4) has r 3 and u 4 radians. There-
fore, its rectangular coordinates are
(r cos u, r sin u) (3 cos 4, 3 sin 4) (1.9609, 2.2704). ■
EXAMPLE 2
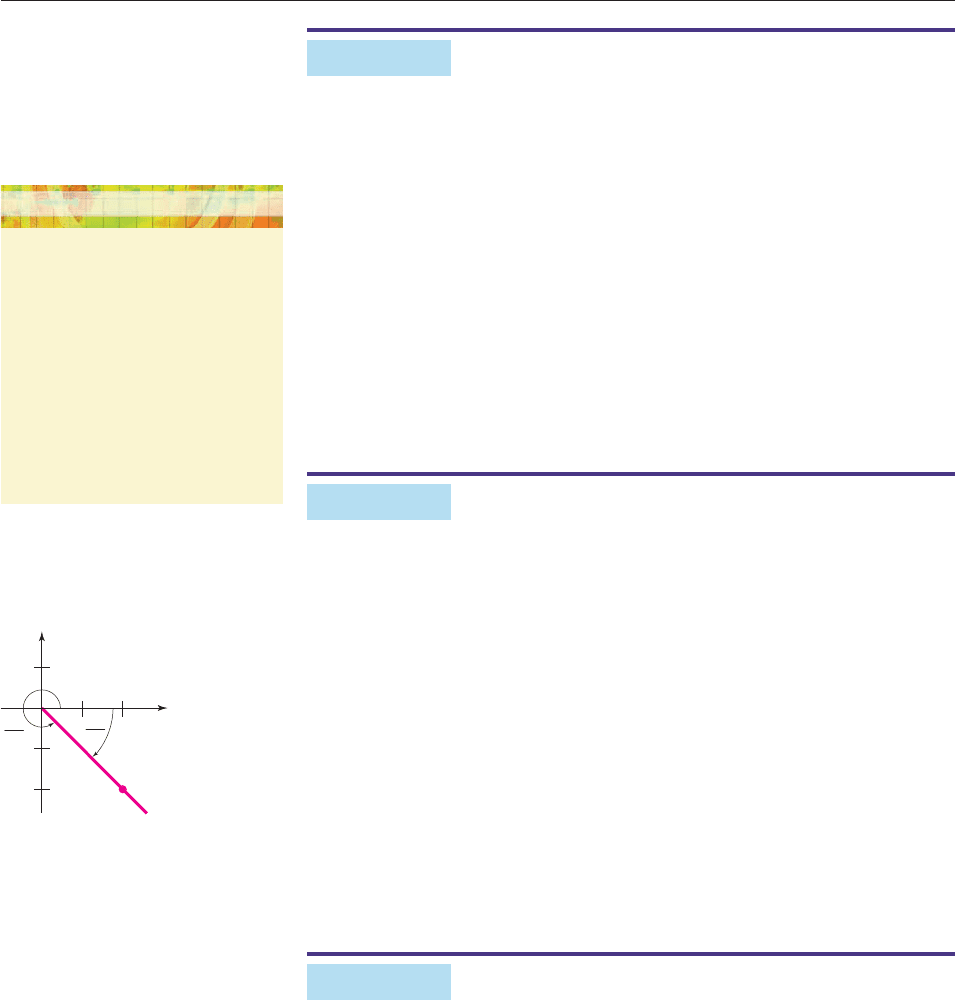
Find the polar coordinates of the point with rectangular coordinates (2, 2).
SOLUTION The second set of equations in the box, with x 2, y 2,
shows that
r
2
2
(
2)
2
8
22
and tan u 2/2 1.
We must find an angle u whose terminal side passes through (2, 2) and whose
tangent is 1. Figure 10–84 shows that two of the many possibilities are
u
p
4
and u
7
4
p
.
So one pair of polar coordinates is
22
,
p
4
, and another is
22
,
7
4
p
. ■
Rectangular to polar conversion is relatively easy when special angles are
involved, as in Example 2. In other cases technology may be necessary.
EXAMPLE 3
Find the polar coordinates of the points whose rectangular coordinates are
(a) (3, 5) (b) (2, 4)
SOLUTION
(a) Applying the second set of equations in the box, with x 3, y 5, we have
r
3
2
5
2
34 and tan u 5/3.
The TAN
1
key on a calculator shows that u 1.0304 radians is an angle
between 0 and p/2 with tangent 5/3. Since (3, 5) is in the first quadrant, one
pair of (approximate) polar coordinates is (34, 1.0304).
SECTION 10.6 Polar Coordinates 745
TECHNOLOGY TIP
Keys to convert from rectangular to
polar coordinates, or vice versa, are in
this menu/submenu:
TI-84: ANGLE
TI-86: VECTOR/OPS
TI-89: MATH/ANGLE
Casio: OPTN/ANGLE
Conversion programs for HP-39gs are
in the Program Appendix.
−2
(2, −2)
2
7π
4
−π
4
x
y
Figure 10–84
