Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

Algebraic techniques were successful in Examples 1 and 2 because substitu-
tion led to equations whose solutions could be found exactly. When this is not the
case, graphical methods are needed. The solutions of a system of equations are the
points that are on the graphs of all the equations in the system. They can be approx-
imated with a graphical intersection finder.
EXAMPLE 3
Solve the system
y x
4
4x
3
9x 1
y 3x
2
3x 7.
SOLUTION If you try substitution on this system, say, by substituting the
expression for y from the first equation into the second, you obtain
x
4
4x
3
9x 1 3x
2
3x 7
x
4
4x
3
3x
2
12x 6 0.
This fourth-degree equation cannot be readily solved algebraically, so a graphical
approach is appropriate.
Graph both equations of the original system on the same screen. In the view-
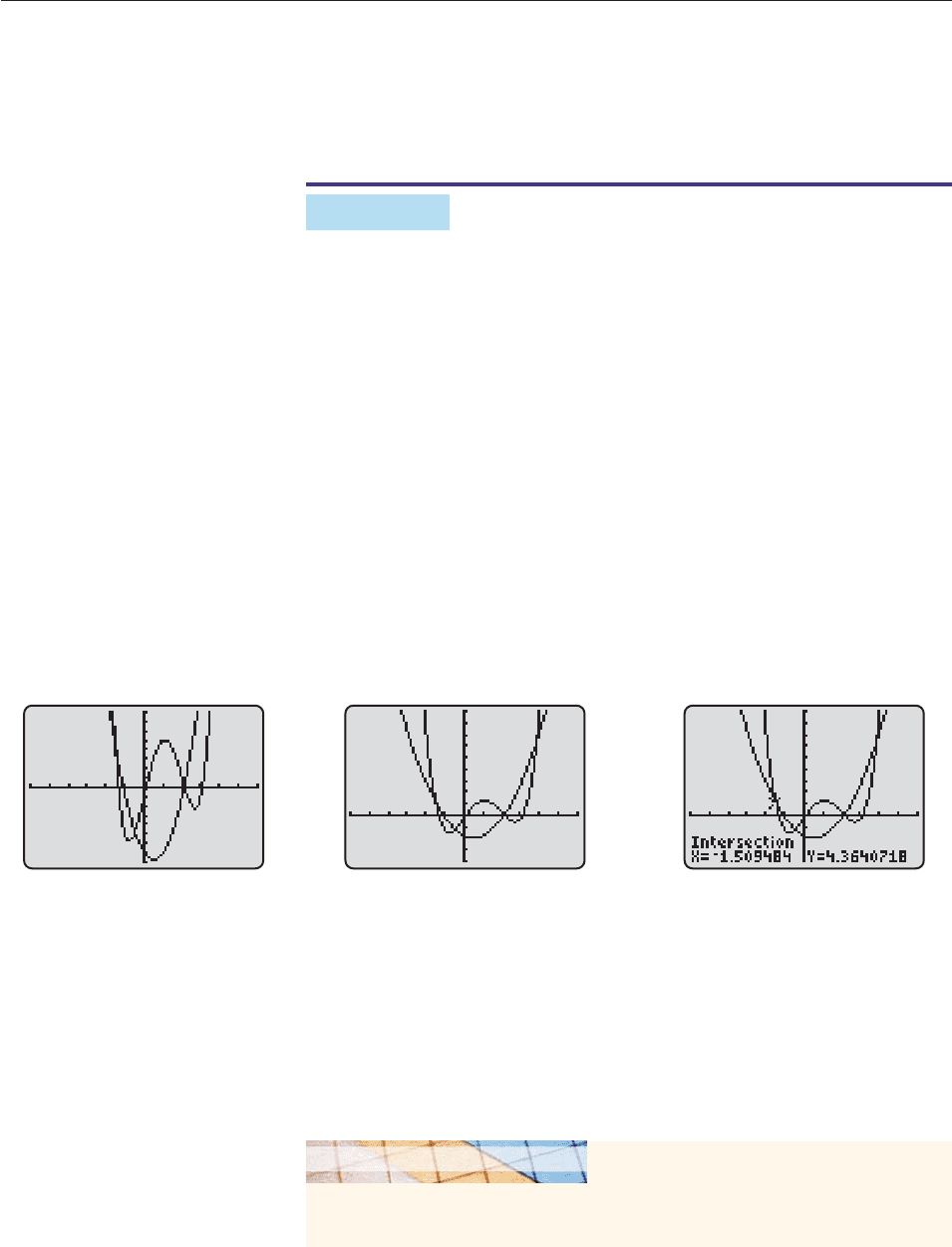
ing window of Figure 11–5, the graphs intersect at three points. However, the
graphs seem to be getting closer together as they run off the screen at the top right,
which suggests that there may be another intersection point.
Figure 11–5 Figure 11–6 Figure 11–7
The larger window in Figure 11–6 shows four intersection points. There cannot be
any more because, as we saw in the previous paragraph, the intersection points
(solutions of the system) correspond to the solutions of a fourth-degree polyno-
mial equation, which has a maximum of four solutions. An intersection finder
(Figure 11–7) shows that one of the approximate solutions of the system is
x 1.509484, y 4.3640718.
−16
−66
36
−16
−66
36
−8
−66
8
786 CHAPTER 11 Systems of Equations
Graph the two equations in the viewing window of Figure 11–6 and use your inter-
section finder to approximate the other three solutions of this system.
GRAPHING EXPLORATION
■
SYSTEMS WITH SECOND-DEGREE EQUATIONS
Solving systems of equations graphically depends on our ability to graph each
equation in the system. With some equations of higher degree, this may require
special techniques.
EXAMPLE 4
Solve this system graphically.
x
2
4x y 1 0
10x
2
25y
2
100.
SOLUTION It’s easy to graph the first equation, since it can be rewritten as
y x
2
4x 1. To graph the second equation, we must first solve for y.
10x
2
25y
2
100
25y
2
100 10x
2
y
2
100
25
10x
2
y
100
25
10x
2
or y
100
25
10x
2
.
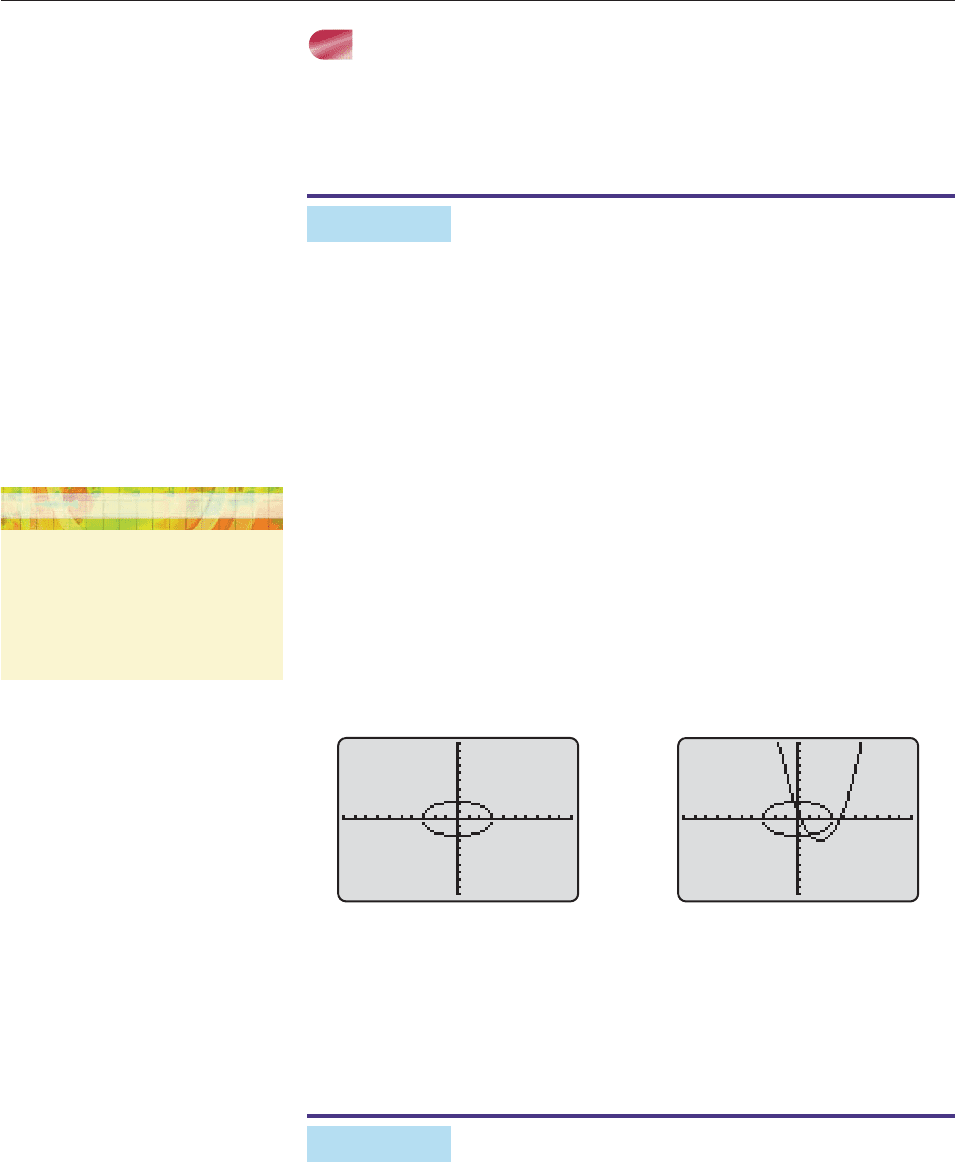
By graphing both these functions on the same screen (see the Technology Tip), we
obtain the complete graph of the equation 10x
2
25y
2
100, as shown in Fig-
ure 11–8. The graphs of both equations in the system are shown in Figure 11–9.
Figure 11–8 Figure 11–9
The two intersection points (solutions of the system) in Figure 11–9 can now be
determined by an intersection finder.
x .2348, y 1.9945 and x .9544, y 1.9067. ■
EXAMPLE 5
To solve the system
4x
2
24xy 3y
2
48 0
16x
2
24xy 9y
2
100x 50y 100 0,
−10
−10 10
10
−10
−10 10
10
SPECIAL TOPICS 11.1.A Systems of Nonlinear Equations 787
TECHNOLOGY TIP
On most calculators, you can graph
both of these functions at once by key-
ing in
y {1, 1}
100
25
10x
2
.
we must express each equation in terms of functions in order to graph it. The first
equation may be rewritten as
3y
2
(24x)y (4x
2
48) 0.
This is a quadratic equation of the form ay
2
by c 0, with
a 3, b 24x, c 4x
2
48,
and hence can be solved by using the quadratic formula.
y
b
2a
b
2
4
ac
y
.
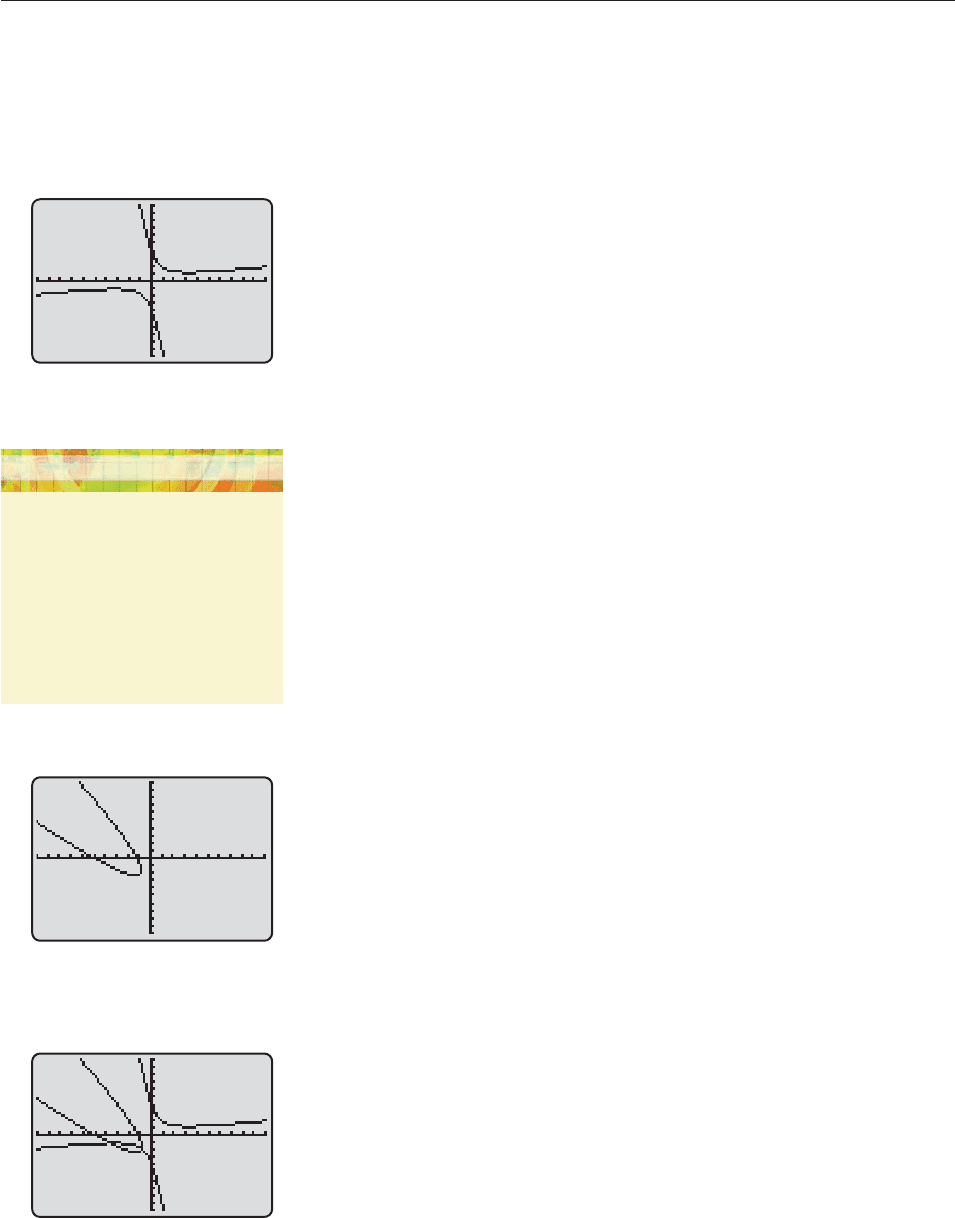
Consequently, the graph of the first equation can be obtained by graphing both of
these functions on the same screen (Figure 11–10).
y .
(
*
)
y .
The second equation can also be solved for y by rewriting it as follows.
16x
2
24xy 9y
2
100x 50y 100 0
9y
2
(24xy 50y) (16x
2
100x 100) 0
9y
2
(24x 50)y (16x
2
100x 100) 0.
Now apply the quadratic formula with a 9, b 24x 50, and c 16x
2
100x 100.
y
b
2a
b
2
4
ac
.
Thus, the graph of the second equation (Figure 11–11) consists of the graphs of
these two functions.
y
(
**
)
y .
By graphing both equations (that is, all four functions shown in (
*
) and (
**
)), we
obtain Figure 11–12. Then an intersection finder shows that the solutions of the
system (points of intersection) are
x 3.623, y 1.113 and x .943, y 1.833. ■
(24x 50)
(24x
50)
2
36(16
x
2
1
00x
100)
18
(24x 50)
(24x
50)
2
36(16
x
2
1
00x
100)
18
(24x 50)
(24x
50)
2
4
9(
16x
2
100x
100)
2
9
24x
(24x)
2
12(
4x
2
48)
6
24x
(24x)
2
12(
4x
2
48)
6
24x
(24x)
2
12(
4x
2
48)
6
24x
(24x)
2
4
3
(
4x
2
48)
2
3
788 CHAPTER 11 Systems of Equations
−10
−10 10
10
Figure 11–10
−10
−10 10
10
Figure 11–12
−10
−10 10
10
Figure 11–11
TECHNOLOGY TIP
TI-8486 users can save keystrokes
by entering the first equation of (
*
) as
y
1
and then using the RCL key to copy
the text of y
1
to y
2
. On TI-89, use COPY
and PASTE in place of RCL. Then only
one sign needs to be changed to make
y
2
into the second equation to be
graphed.
APPLICATIONS
EXAMPLE 6
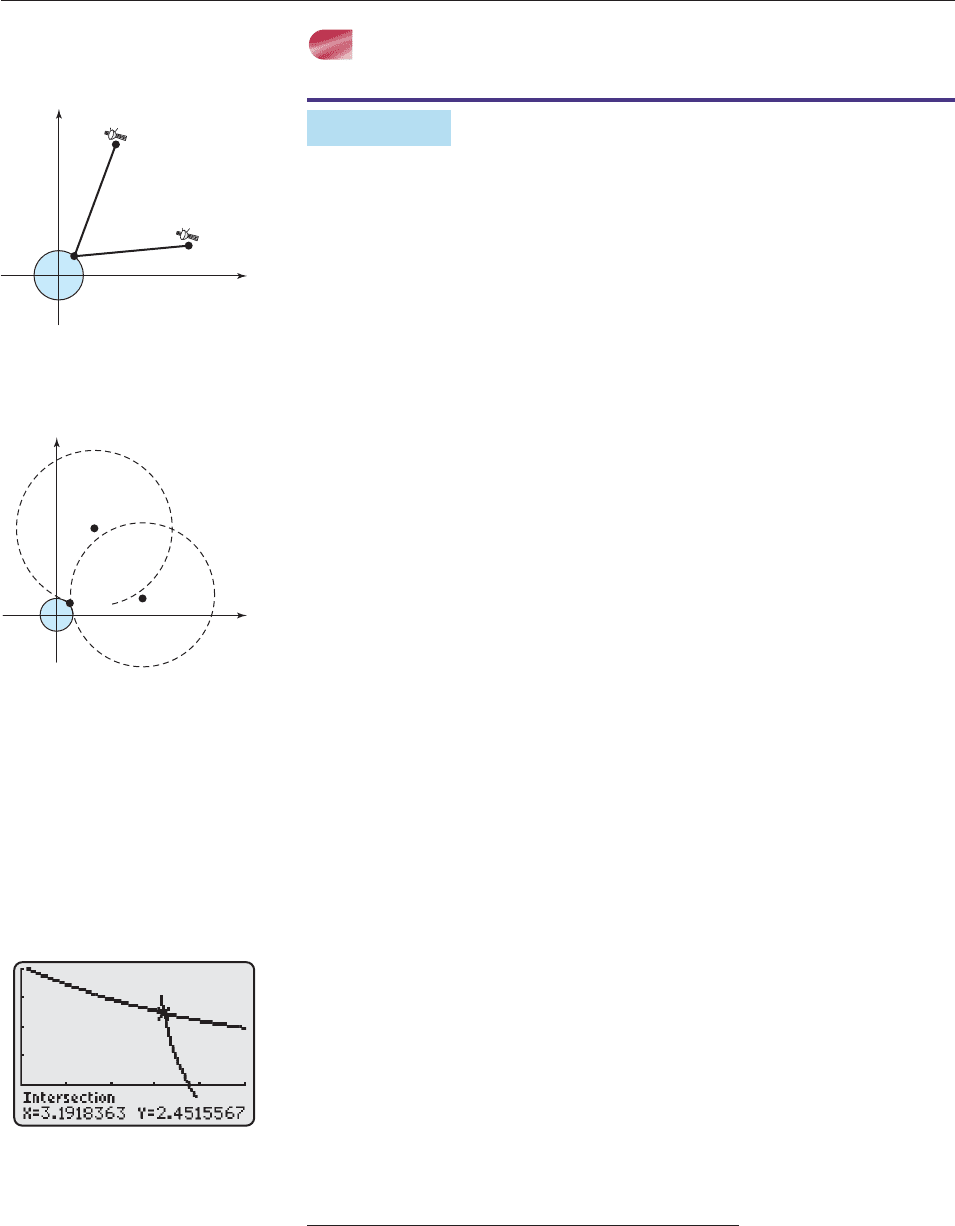
Suppose the earth is a flat, circular disc of radius 4000 miles, centered at the ori-
gin of a two-dimensional coordinate system in which 1 unit represents 1000
miles. Figure 11–13 (which is not to scale) shows a GPS device at point (x, y) and
two satellites at (8, 15.6) and (16.2, 4). Radio signals show that the distances of
the satellites to (x, y) are 14 thousand and 13.1 thousand miles respectively, as
shown in the figure. What are the coordinates of the device?
SOLUTION The distance from (x, y) to (8, 15.6) is 14. By the distance
formula,
(x 8
)
2
(y
15.
6)
2
14
Square both sides: (x 8)
2
(y 15.6)
2
14
2
.
Thus, (x, y) lies on the circle with center (8, l5.6) and radius 14. Similarly, since
the distance from (x, y) to (16.2, 4) is 13.1,
(x 1
6.2)
2
(y 4
)
2
13.1
(x 16.2)
2
(y 4)
2
13.1
2
.
So (x, y) also lies on the circle with center (16.2, 4) and radius 13.1.
Therefore, (x, y) is one of the intersection points of these two circles, as shown
in Figure 11–14*. We must find this intersection point, that is, solve the system
(x 8)
2
(y 15.6)
2
14
2
(x 16.2)
2
(y 4)
2
13.1
2
.
To solve this system graphically, we first solve each equation for y.
(x 8)
2
(y 15.6)
2
14
2
(y 15.6)
2
14
2
(x 8)
2
y 15.6 14
2
(x 8
)
2
y 14
2
(x 8
)
2
15.6 or y 14
2
(x 8
)
2
15.6.
A similar computation with the equation (x 16.2)
2
(y 4)
2
13.1
2
shows
y
13.1
2
(x 1
6.2)
2
4ory 13.1
2
(x 1
6.2)
2
4.
Graphing the four preceding equations should produce something similar to
Figure 11–14. Because of limited resolution, however, a graphing calculator will
show only parts of the circles (try it!). Fortunately, we are interested only in the
intersection point closest to the origin. Using an intersection finder in the partial
graph in Figure 11–15, shows that this point is
(x, y) (3.1918, 2.4516). ■
SPECIAL TOPICS 11.1.A Systems of Nonlinear Equations 789
(x, y)
(8, 15.6)
(16.2, 4)
14
13.1
y
x
Figure 11–13
(x, y)
(8, 15.6)
(16.2, 4)
y
x
Figure 11–14
4
05
Figure 11–15
*In our actual three-dimensional world, the GPS location would be an intersection point of three or
more spheres, i.e., a solution of a system of three or more second-degree equations in three variables.
790 CHAPTER 11 Systems of Equations
−50
−40 40
50
Figure 11–16
EXAMPLE 7
A 52-foot-long piece of wire is to be cut into three pieces, two of which are the
same length. The two equal pieces are to be bent into squares and the third piece
into a circle. What should the length of each piece be if the total area enclosed by
the two squares and the circle is 100 square feet?
SOLUTION Let x be the length of each piece of wire that is to be bent into a
square, and let y be the length of the piece that is to be bent into a circle. Since the
original wire is 52 feet long,
x x y 52 or, equivalently, y 52 2x.
If a piece of wire of length x is bent into a square, the side of the square will have
length x/4 and hence the area of the square will be (x/4)
2
x
2
/16. The remain-
ing piece of wire will be made into a circle of circumference (length) y. Since the
circumference is 2p times the radius (that is, y 2pr), the circle has radius
r y/2p. Therefore, the area of the circle is
pr
2
p
2
y
p
2
p
4p
y
2
2
4
y
p
2
.
The sum of the areas of the two squares and the circle is 100, that is,
1
x
6
2
1
x
6
2
4
y
p
2
100
4
y
p
2
100
2
1
x
6
2
y
2
4p
100
x
8
2
.
Therefore, the lengths x and y are solutions of this system of equations.
y 52 2x
y
2
4p
100
x
8
2
.
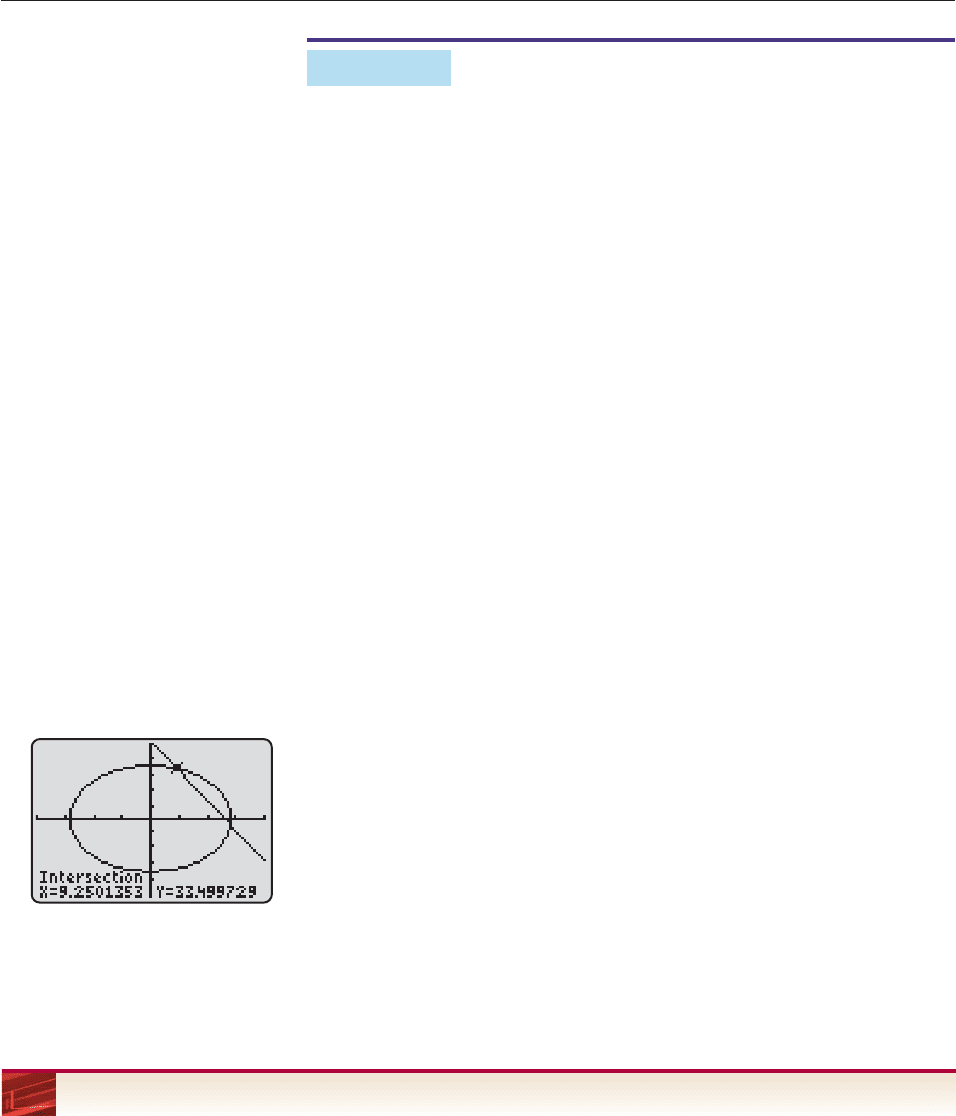
The system may be solved either algebraically or graphically, using Fig-
ure 11–16. Since x and y are lengths, both must be positive. Consequently, we
need only consider the intersection point in the first quadrant. An intersection
finder shows that its coordinates are x 9.25, y 33.50. Therefore, the wire
should be cut into two 9.25-foot pieces and one 33.5-foot piece. ■
EXERCISES 11.1.A
In Exercises 1–12, solve the system algebraically.
1. x
2
y 0 2. x
2
y 0
2x y 33x y 18
3. x
2
y 0 4. x
2
y 0
x 2y 5 x 5y 7
5. x y 10 6. 2x y 5
xy 21 xy 3
7. xy y
2
9 8. xy 3x
2
2
x 2y 64x y 1

9. x
2
y
2
4x 4y 4
x y 2
10. x
2
y
2
4x y 1
x 3y 2
11. x
2
y
2
25 12. x
2
y
2
4
x
2
y 19 x
2
y 10
In Exercises 13–28, solve the system by any means.
13. y x
3
3x
2
4
y .5x
2
3x 2
14. y x
3
5x
2
x 4
y 3x
2
2
15. y x
3
3x 2
y
x
2
3
3
16. y .5x
4
x
2
5
y x
3
2x
2
3x 2
17. y x
3
x 1
y sin x
18. y x
3
2x
2
1
y cos x
19. 25x
2
16y
2
400
9x
2
4y
2
36
20. 5x
2
8y
2
100
2x
2
4y
2
1
21. 3x
2
4y
2
18x 14y 1
x y 3
22. 3x
2
6y
2
40
2x y 3
23. x
2
4xy 4y
2
30x 90y 450 0
x
2
x y 1 0
24. 4x
2
xy 4y
2
2x 3y 50 0
x
2
3x y 0
25. 4x
2
6xy 2y
2
3x 10y 6
4x
2
y
2
64
26. 4x
2
xy y
2
x 2y 3 0
3x
2
5xy y
2
3x 4y 6 0
27. x
2
3xy y
2
2
3x
2
5xy 3y
2
7
SPECIAL TOPICS 11.1.A Systems of Nonlinear Equations 791
28. 2x
2
8xy 8y
2
2x 5 0
16x
2
24xy 9y
2
100x 200y 100 0
29. Suppose that the first satellite in Example 6 is located at
(2.7, 15.9) and is 12.7 thousand miles from the GPS device.
If the second satellite is at (13.9, 9.9) and is 13.3 thousand
miles from the device, what are the coordinates of the
device?
30. Internet sales of apparel (in billions of dollars) are projected
to be given by
f(x) .38x
2
.35x 4.85.
where x 2 corresponds to 2002.* Similarly, sales of
computer-related items are projected to be given by
g(x) .17x
2
2.73x 2.71.
In what year were Internet sales of apparel and computer-
related items at the same level?
31. A rectangular box (including top) with square ends and a vol-
ume of 16 cubic meters is to be constructed from 40 square
meters of cardboard. What should its dimensions be?
32. A rectangular sheet of metal is to be rolled into a circular
tube. If the tube is to have a surface area (excluding ends) of
210 square inches and a volume of 252 cubic inches, what
size sheet of metal should be used?
33. Find two real numbers whose sum is 17 and whose prod-
uct is 52.
34. Find two real numbers whose sum is 34.5 and whose prod-
uct is 297.
35. Find two real numbers whose difference is 25.75 and whose
product is 127.5.
36. Find two real numbers whose sum is 3 such that the sum of
their squares is 369.
37. Find two real numbers whose sum is 2 such that the differ-
ence of their squares is 60.
38. Find the dimensions of a rectangular room whose perimeter
is 58 feet and whose area is 204 square feet.
39. Find the dimensions of a rectangular room whose perimeter
is 53 feet and whose area is 165 square feet.
40. A rectangle has area 120 square inches and a diagonal of
length 17 inches. What are its dimensions?
41. A right triangle has area 225 square centimeters and a
hypotenuse of length 35 centimeters. To the nearest tenth of
a centimeter, how long are the legs of the triangle?
42. Find the equation of the straight line that intersects the
parabola y x
2
only at the point (3, 9). [Hint: What condi-
tion on the discriminant guarantees that a quadratic equa-
tion has exactly one real solution?]
*Based on data from Forrester Research.

792 CHAPTER 11 Systems of Equations
11.2 Large Systems of Linear Equations
■ Use Gaussian elimination to solve large systems of linear
equations.
■ Use matrix methods to solve systems of linear equations.
■ Identify matrices that are in row echelon or reduced row echelon
form.
■ Use the Gauss-Jordan method to solve systems of linear
equations.
■ Identify inconsistent and dependent systems.
■ Use systems of linear equations to solve applied problems.
Systems of linear equations in three variables can be interpreted geometrically as
the intersection of planes. However, algebraic methods are the only practical
means to solve such systems or ones with more variables. Large systems can be
solved by Gaussian elimination,* which is an extension of the elimination
method used in Section 11.1.
Two systems of equations are said to be equivalent if they have the same
solutions. The basic idea of Gaussian elimination is to transform a given system
into an equivalent system that can easily be solved. There are several operations
on a system of equations that leave the solutions to the system unchanged and,
hence, produce an equivalent system. The first one is to
Interchange any two equations in the system,
which obviously won’t affect the solutions of the system. The second is to
Multiply an equation in the system by a nonzero constant.
This does not change the solutions of the equation and therefore does not change
the solutions of the system. To understand how the next operation works, we shall
examine an earlier example from a different viewpoint.
EXAMPLE 1
In Example 3 of Section 11.1, we solved the system
x 3y 4
2x y 1
by multiplying the first equation by 2 and adding it to the second to eliminate
the variable x.
2x 6y 8 [2 times first equation]
2x y 1 [Second equation]
7y 7. [Sum of second equation and 2 times first equation]
Section Objectives
*Named after the German mathematician K. F. Gauss (1777–1855).

We then solved this last equation for y and substituted the answer, y 1, in the
original first equation to find that x 1. What we did, in effect, was
Replace the original system by the following system, in which x
has been eliminated from the second equation; then solve this
new system.
(
*
)
x 3y 4 [First equation]
7y 7. [Sum of second equation and 2 times first equation]
The solution of system (
*
) is easily seen to be y 1, x 1, and you can read-
ily verify that this is the solution of the original system. So the two systems are
equivalent. [Note: We are not claiming that the second equations in the two sys-
tems have the same solutions—they don’t—but only that the two systems have the
same solutions.] ■
Example 1 is an illustration of the third of the following operations.
The next example shows how elementary operations can be used to transform
a system into an equivalent system that can be solved.
EXAMPLE 2
Solve the system
x 4y 3z 1 [Equation A]
3x 6y z 3 [Equation B]
2x 11y 5z 0. [Equation C]
SOLUTION We first use elementary operations to produce an equivalent sys-
tem in which the variable x has been eliminated from the second and third equations.
To eliminate x from equation B, replace equation B by the sum of itself and
3 times equation A.
[3 times A] 3x 12y 9z 3
[B] 3x 6y z 3
6y 8z 6
x 4y 3z 1 [A]
6y 8z 6 [Sum of B and 3 times A]
2x 11y 5z 0. [C]
SECTION 11.2 Large Systems of Linear Equations 793
Elementary
Operations
Performing any of the following operations on a system of equations
produces an equivalent system.
1. Interchange any two equations in the system.
2. Replace an equation in the system by a nonzero constant multiple of
itself.
3. Replace an equation in the system by the sum of itself and a constant
multiple of another equation in the system.

To eliminate x from equation C, we replace equation C by the sum of itself and 2
times equation A.
[2 times A] 2x 8y 6z 2
[C] 2x 11y 5z 0
3y z 2
x 4y 3z 1
6y 8z 6
3y z 2.
[Sum of C and 2 times A]
The next step is to eliminate the y term in one of the last two equations. This can
be done by replacing the second equation by the sum of itself and 2 times the
third equation.
x 4y 3z 1
10z 10
3y z 2.
Finally, interchange the last two equations.
x 4y 3z 1
(
*
) 3y z 2
10z 10.
This last system, which is equivalent to the original one, is easily solved. The last
equation shows that
10z 10 or, equivalently, z 1.
Substituting z 1 in the second equation shows that
3y z 2
3y (1) 2
3y 1
y
1
3
.
Substituting y 1/3 and z 1 in the first equation yields
x 4y 3z 1
x 4
1
3
3(1) 1
x 1
4
3
3
2
3
.
Therefore, the original system has just one solution: x 2/3, y 1/3,
z 1. ■
The process used to solve the final system (
*
) in Example 2 is called back sub-
stitution because you begin with the last equation and work back to the first. It
works because system (
*
) is in triangular form: The first variable in the first
794 CHAPTER 11 Systems of Equations
[Sum of second equation and
2 times third equation]
equation, x, does not appear in any subsequent equation; the first variable in the
second equation, y, does not appear in any subsequent equation, and so on. It can
be shown that the procedure in Example 2 works in every case.
SECTION 11.2 Large Systems of Linear Equations 795
Gaussian
Elimination
Any system of linear equations can be transformed into an equivalent sys-
tem in triangular form by using a finite number of elementary operations.
If the system has solutions, they can then be found by back substitution in
the triangular form system.
Most people prefer to use a calculator or computer to solve large systems
of equations. However, the system solvers on some calculators are limited
(see the Technology Tip in the margin). So we now develop a version of Gaussian
elimination that works with all systems and is easily implemented on a
calculator.
MATRIX METHODS
When solving systems by hand, a lot of time is wasted copying the x’s, y’s, z’s, and
so on. This fact suggests a shorthand system for representing a system of equa-
tions. For example, the system
x 2y 3z 2
(
*
) 2x 6y z 2
3x 3y 10z 2
can be represented by the following rectangular array of numbers, consisting of
the coefficients of the variables and the constants on the right of the equal sign,
arranged in the same order in which they appear in the system.
12 3 2
26 1 2
3310 2
This array is called the augmented matrix of the system. It has three horizontal
rows and four vertical columns.
EXAMPLE 3
Use the matrix form of the preceding system (
*
) to solve the system.
SOLUTION To solve the system in its original equation form, we would use
elementary operations to eliminate the x terms from the last two equations, and
then eliminate the y term from the last equation. With matrices, we do essentially
the same thing, with the elementary operations on equations being replaced by the
corresponding row operations on the augmented matrix in order to make certain
TECHNOLOGY TIP
To solve a system of linear equations
on a calculator, use:
TI-84: POLYSMLT (APPS menu*)
TI-86: SIMULT (Keyboard)
Casio: EQUA (Main menu)
The TI-84 PolySmlt solver can han-
dle all systems (but see the Tip on
page 800). Other solvers can handle
only systems with the same number of
equations as variables (when they
display an error message, the system
may have no solutions or it may have
infinitely many solutions).
TECHNOLOGY TIP
To enter and store a matrix in the
matrix editor, use MAT(RIX), which is
located here:
TI: Keyboard
HP-39gs: Keyboard
Casio 9850: main menu.
*If it’s not in the APPS menu, it can be downloaded from TI.
