Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

806 CHAPTER 11 Systems of Equations
57. A furniture manufacturer has 1950 machine hours available
each week in the cutting department, 1490 hours in the as-
sembly department, and 2160 in the finishing department.
Manufacturing a chair requires .2 hours of cutting, .3 hours
of assembly, and .1 hours of finishing. A chest requires
.5 hours of cutting, .4 hours of assembly, and .6 hours of
finishing. A table requires .3 hours of cutting, .1 hours of as-
sembly, and .4 hours of finishing. How many chairs, chests,
and tables should be produced to use all the available pro-
duction capacity?
58. A stereo equipment manufacturer produces three models of
speakers, R, S, and T, and has three kinds of delivery vehi-
cles: trucks, vans, and station wagons. A truck holds two
boxes of model R, one of model S, and three of model T. A
van holds one box of model R, three of model S, and two of
model T. A station wagon holds one box of model R, three
of model S, and one of model T. If 15 boxes of model R, 20
boxes of model S, and 22 boxes of model T are to be deliv-
ered, how many vehicles of each type should be used so that
all operate at full capacity?
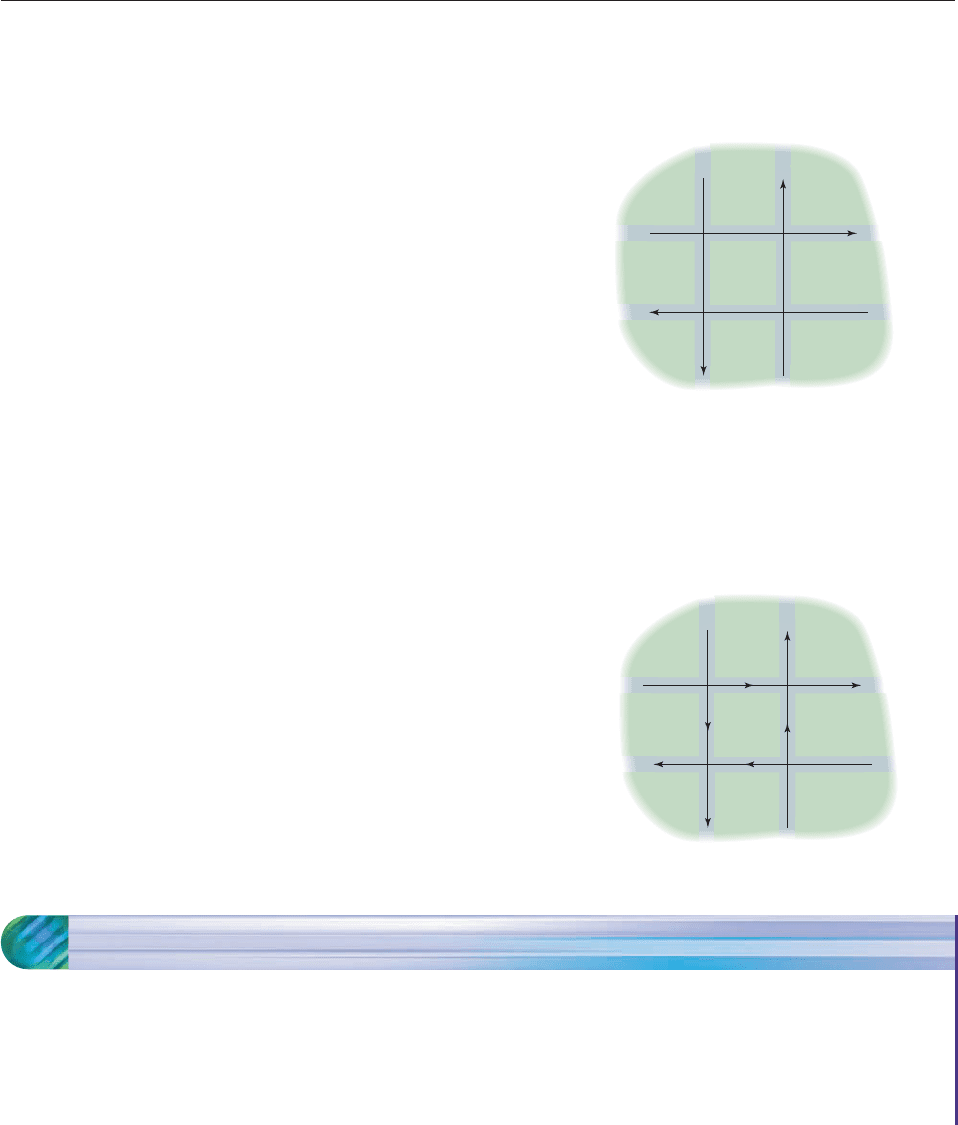
59. The diagram shows the traffic flow at four intersections dur-
ing a typical one-hour period. The streets are all one-way, as
indicated by the arrows. To adjust the traffic lights to avoid
congestion, engineers must determine the possible values of
x, y, z, and t.
(a) Write a system of linear equations that describes con-
gestion-free traffic flow. [Hint: 600 cars per hour come
down Euclid to intersection A, and 400 come down 4th
Avenue to intersection A. Also, x cars leave intersection
A on Euclid, and t cars leave on 4th Avenue. To avoid
congestion, the number of cars leaving the intersection
must be the same as the number entering, that is, x t
600 400. Use intersections B, C, and D to find three
more equations.]
(b) Solve the system in part (a), which is dependent.
Express your answers in terms of the variable t.
(c) Find the largest and smallest number of cars that can
leave the given intersection on the given street: A on 4th
Avenue, A on Euclid, C on 5th Avenue, and C on
Chester.
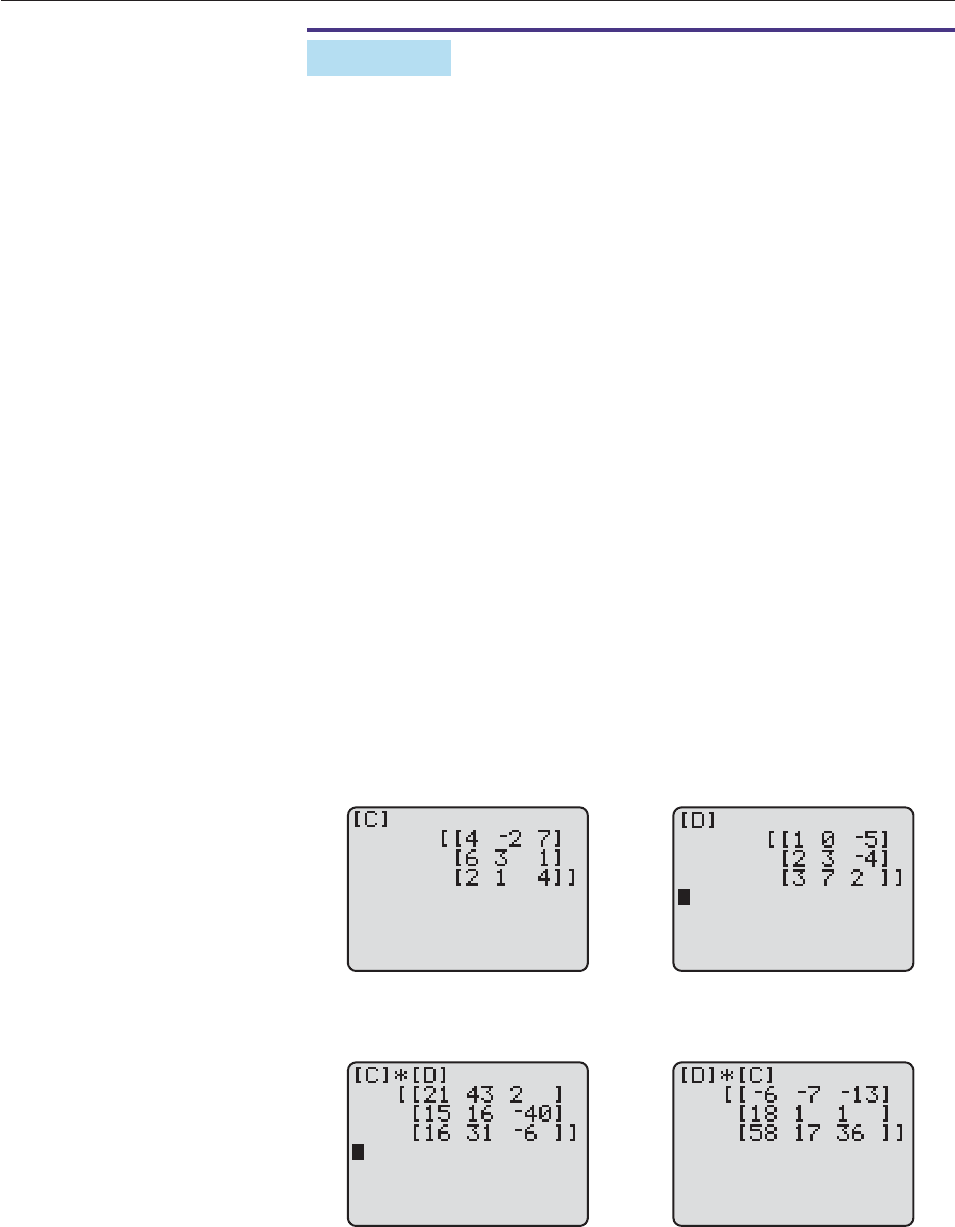
60. The diagram shows the traffic flow at four intersections
during rush hour, as in Exercise 59.
(a) What are the possible values of x, y, z, and t in order to
avoid any congestion? [Express your answers in terms
of t.]
(b) What are the possible values of t?
500 out
x
z
t
y
1200 in
600 in
1500 out
Clinton Raynor
700 out
1400 in
400 in
900 out
J
efferson
Harvey
700 out
AB
x
z
t
y
600 in
400 in
300 out
DC
4th Ave 5th Ave
400 out
200 in
500 in
300 out
Chester
Euclid
11.3 Matrix Methods for Square Systems
■ Perform matrix multiplication.
■ Find the inverse of an invertible matrix.
■ Write certain systems of equations in matrix form and use matrix
inverses to solve them.
■ Find the equation of a parabola, given three points on it.
Matrices were used in Section 11.2 as a convenient shorthand for solving systems
of linear equations. We now consider matrices in a more general setting and show
how the algebra of matrices provides an alternative method for solving systems of
equations that are not dependent and have the same number of equations as
variables.
Section Objectives

Let m and n be positive integers. An m n matrix (read “m by n matrix”) is
a rectangular array of numbers, with m horizontal rows and n vertical columns.
For example,
3 3 matrix 5 2 matrix 3 4 matrix 4 1 matrix
3 rows 5 rows 3 rows 4 rows
3 columns 2 columns 4 columns 1 column
In a matrix, the rows are horizontal and are numbered from top to bottom. The
columns are vertical and are numbered from left to right. For example,
Row 1 11 3 14
Row 2
205
Row 3
1
3
67
Column 1 Column 2 Column 3
Each entry in a matrix can be located by stating the row and column in which
it appears. For instance, in the preceding 3 3 matrix, 14 is the entry in row 1,
column 3, and 0 is the entry in row 2, column 2. When you enter a matrix on a cal-
culator, the words “row” and “column” won’t be displayed, but the row numbers
will always be listed before the column number. Thus, a display such as “A[3, 2],”
or simply “3, 2,” indicates the entry in row 3, column 2.
Two matrices are said to be equal if they have the same size (same number of
rows and columns) and the corresponding entries are equal. For example,
3(1)
2
3 1 64 65
, but
.
612 36 12 51 41
MATRIX MULTIPLICATION
Although there is an extensive arithmetic of matrices, we shall need only matrix
multiplication. The simplest case is the product of a matrix with a single row and a
matrix with a single column, where the row and column have the same number of
entries. This is done by multiplying corresponding entries (first by first, second by
second, and so on) and then adding the results. An example is shown in Figure 11–24.
2
(3 1 2)
0
3
2 1
0 2
1 8
1
First Second Third
Terms Terms Terms
Figure 11–24
Note that the product of a row and a column is a single number.
Now let A be an m n matrix, and let B be an n p matrix, so that the num-
ber of columns of A is the same as the number of rows of B (namely, n). The prod-
uct matrix AB is defined to be an m p matrix (same number of rows as A and
same number of columns as B). The product AB is defined as follows.
SECTION 11.3 Matrix Methods for Square Systems 807
325
61 7
25 0
34
20
01
73
1 6
3010
2
1
2
4
8
3
10 2
3
4
12
3
2
0
11

EXAMPLE 1
If it is defined, find the product AB, where
312
A
and B .
104
SOLUTION A has 3 columns, and B has 3 rows. So the product matrix AB is
defined. AB has 2 rows (same as A) and 4 columns (same as B). Its entries are cal-
culated as follows. The entry in row 1, column 1 of AB is the product of row 1 of
A and column 1 of B, which is the number 8, as shown in Figure 11–24 and indi-
cated at the right here below.
2 301
0527
1841
808 CHAPTER 11 Systems of Equations
312
row 1, column 1
104
312
row 1, column 2
104
312
row 1, column 3
104
312
row 1, column 4
104
312
row 2, column 1
104
312
row 2, column 2
104
312
row 2, column 3
104
312
row 2, column 4
104
The other entries in AB are obtained similarly.
2 301
0527
1841
2 301
0527
1841
2 301
0527
1841
2 301
0527
1841
2 301
0527
1841
2 301
0527
1841
2 301
0527
1841
2 301
0527
1841
8
3
2 1
0 2
1 8
812
3(3) 1
5 2
8 12
812 6
3
0 1
2 2(4) 6
812 612
3
1 1
7 2
1 12
812 612
(1)2 0
0 4
1 2
2
812 612
(1)(3) 0
5 4
8 35
235
812 612
(1)0 0
2 4(4) 16
23516
812 612
(1)1 0
7 4
1 3
23516 3
Matrix
Multiplication
If A is an m n and B is an n p matrix, then AB is the m p matrix
whose entry in the ith row and jth column is
the product of the ith row of A and the j th column of B.
The last matrix on the right is the product AB. ■
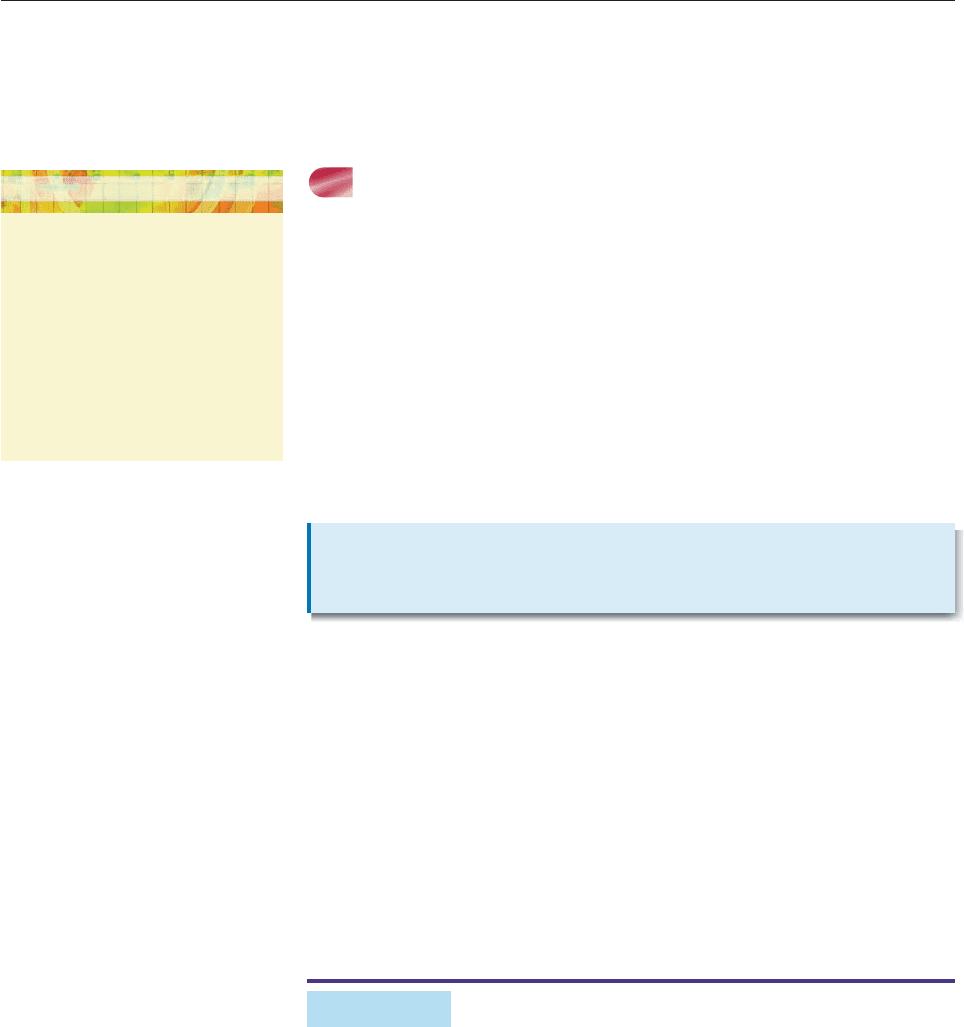
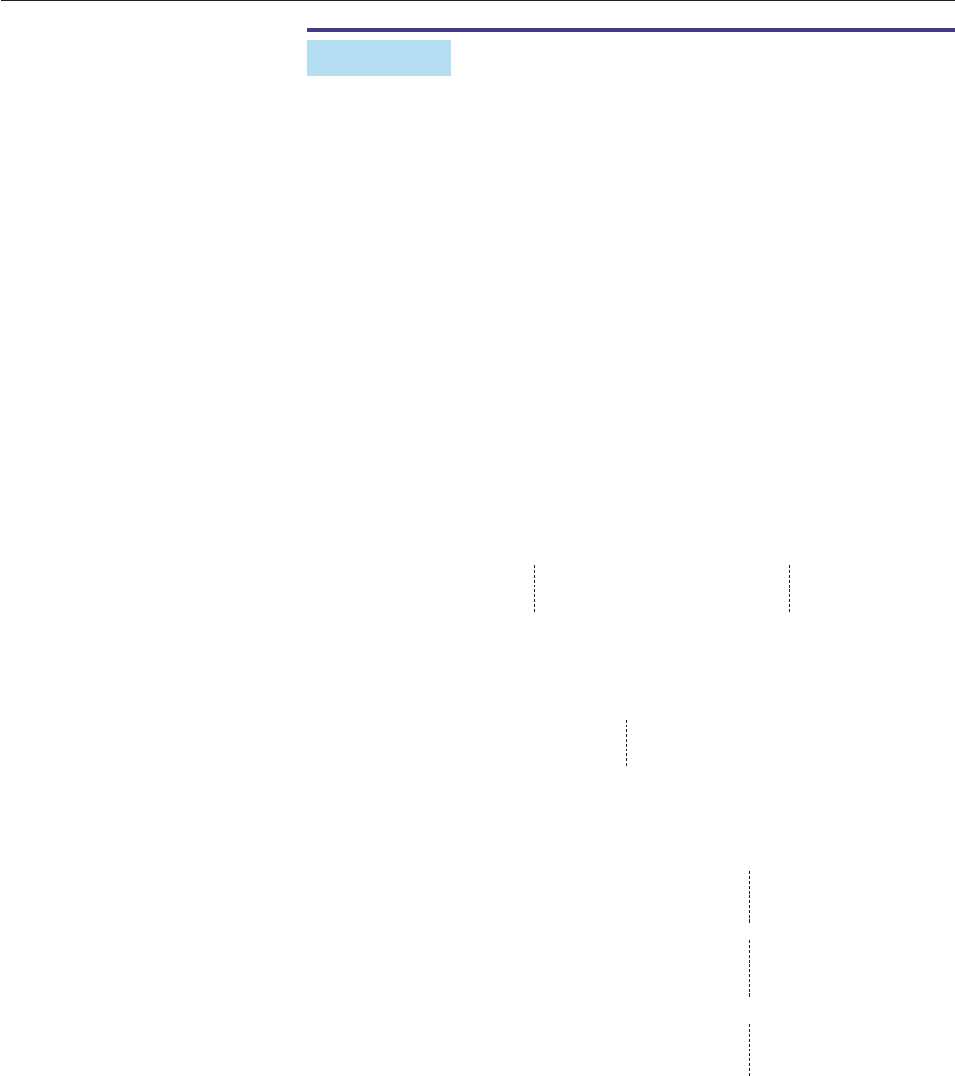
EXAMPLE 2
Let A, B, C, and D be the following matrices.
321 52427
A
204
, B
1 1
, C
631
,
1 25 4 2 2 14
105
D
234
37 2
Find each of the following matrices, if possible.
(a) AB (b) BC (c) CD and DC
SOLUTION
(a) Following the same procedure as in Example 1, we have
32152
AB
204
1 1
1 25 4 2
3
5 2
1 1
43(2) 2(1) 1
2
(2)
5 0
1 4
4(2)(2) 0(1) 4
2
1
5 (2)
1 5
41(2) (2)(1) 5
2
21 6
612
.
23 10
(b) Matrix B is 3 2, and C is 3 3. Since the number of columns in B is dif-
ferent from the number of rows in C, the product is not defined.
(c) We use the matrix editor of a calculator to enter the matrices (Figure 11–25).
Figure 11–25
We then use the calculator to compute both products (Figure 11–26).
Figure 11–26
Note that DC is not equal to CD. ■
SECTION 11.3 Matrix Methods for Square Systems 809
It can be shown that matrix multiplication is associative, meaning that
A(BC) (AB)C for all matrices A, B, C for which the products are defined. As
we saw in Example 2, however, matrix multiplication is not commutative, that is,
AB might not be equal to BA, even when both products are defined.
IDENTITY MATRICES AND INVERSES
The n n identity matrix I
n
is the matrix with 1’s on the diagonal from upper left
to lower right and 0’s everywhere else; for example,
The number 1 is the multiplicative identity of the number system because
a
1 a 1
a for every number a. The identity matrix I
n
is the multiplicative
identity for n n matrices.
For example, in the 2 2 case,
ab 10 a
1 b
0 a
0 b
1 ab
.
cd 01 c
1 d
0 c
0 d
1 cd
Verify that the same answer results if you reverse the order of multiplication.
Every nonzero number c has a multiplicative inverse c
1
1/c with the
property that cc
1
1. The analogous statement for matrix multiplication does
not always hold, and special terminology is used when it does. An n n matrix A
is said to be invertible (or nonsingular) if there is an n n matrix B such that
AB I
n
. In this case, it can be proved that BA I
n
also. The matrix B is called the
inverse of A and is sometimes denoted A
1
.
EXAMPLE 3
You can readily verify that
21 11 10 1121
.
31 3201 32 3 1
21
Therefore, A
is an invertible matrix with inverse
31
11
A
1
. ■
3 2
810 CHAPTER 11 Systems of Equations
10
I
2
,
01
100
I
3
010
,
001
1000
0100
I
4
.
0010
0001
Identity
Matrix
For any n n matrix A,
AI
n
A I
n
A.
TECHNOLOGY TIP
To display an n n identity matrix,
use IDENT(ITY)n or IDENMATn in this
menu/submenu:
TI-84: MATRIX/MATH
TI-86: MATRIX/OPS
TI-89: MATH/MATRIX
Casio: OPTN/MAT
HP-39gs: MATH/MATRIX
EXAMPLE 4
26
Find the inverse of the matrix
.
14
SOLUTION We must find numbers x, y, u, v such that
26 xu 10
,
14 yv 01
which is the same as
2x 6y 2u 6v 10
.
x 4yu 4v 01
Since corresponding entries in these last two matrices are equal, finding x, y, u, v
amounts to solving these systems of equations:
2x 6y 12u 6v 0
and
x 4y 0 u 4v 1.
We shall solve the systems by the Gauss-Jordan method of Section 11.2. The aug-
mented matrices for the two systems are
26 1 26 0
A
and B
.
14 0 14 1
Note that the row operations that are needed for both A and B will be the same
(because the first two columns are the same in both A and B). Consequently, we
can save space and time by combining both of these matrix into this single matrix.
26 10
.
14 01
The first three columns of the last matrix are matrix A, and the first two and last
columns are matrix B. Performing row operations on this matrix amounts to doing
the operations simultaneously on both A and B.
Multiply row 1 by 1/2: 13
1
2
0
14 01
13
1
2
0
01
1
2
1
10 23
01
1
2
1
The first three columns of the last matrix show that x 2 and y 1/2. Simi-
larly, the first two and last columns show that u 3 and v 1. Therefore,
2 3
A
1
.
1
2
1
Observe that A
1
is just the right half of the final form of the preceding augmented
matrix and that the left half is the identity matrix I
2
. ■
SECTION 11.3 Matrix Methods for Square Systems 811
Replace row 2 by the sum of
itself and 1 times row 1:
Replace row 1 by the sum of
itself and 3 times row 2:
Although the technique in Example 4 can be used to find the inverse of any
matrix that has one, it’s quicker to use a calculator. Any calculator with matrix
capabilities can find the inverse of an invertible matrix (see the Technology Tip in
the margin).
812 CHAPTER 11 Systems of Equations
CAUTION
A calculator should produce an error message when asked for the inverse of a matrix A that does
not have one. However, because of round-off errors, it may sometimes display a matrix that it
says is A
1
. As an accuracy check when finding inverses, multiply A by A
1
to see whether the
product is the identity matrix. If it isn’t, A does not have an inverse.
INVERSE MATRICES AND SYSTEMS OF EQUATIONS
Any system of linear equations can be expressed in matrix form, as shown in the
next example.
EXAMPLE 5
Use matrix multiplication to express this system of equations in matrix form.
x y z 2
2x 3y 5
x 2y z 1.
SOLUTION Let A be the 3 3 matrix of coefficients on the left side of the
equations, let B be the column matrix of constants on the right side, and let X be
the column matrix of unknowns.
111 x 2
A
230
, X
y
, B
5
.
121 z 1
Then AX is a matrix with three rows and one column, as is B.
111 xx y z 2
AX
230
y
2x 3y 0z
and B
5
.
121 zx 2y z 1
The entries in AX are just the left sides of the equations of the system, and the
entries in B are the constants on the right sides. Therefore, the system can be
expressed as the matrix equation AX B. ■
Suppose a system of equations is written in matrix form AX B and that the matrix A
has an inverse. Then we can solve AX B by multiplying both sides by A
1
.
A
1
(AX) A
1
B
(A
1
A)X A
1
B [Matrix multiplication is associative]
I
n
X A
1
B [A
1
A is the identity matrix]
X A
1
B [Product of identity matrix and X is X]
The next example shows how this works in practice.
TECHNOLOGY TIP
On calculators other than TI-89, you
can find the inverse A
1
of matrix A by
keying in A (or Mat A) and using the
x
1
key. Using the V key and 1 pro-
duces A
1
on TI-89 and HP-39gs but
leads to an error message on other
calculators.
EXAMPLE 6
Solve the system
x y z 2
2x 3y 5
x 2y z 1.
SOLUTION As we saw in Example 5, this system is equivalent to the matrix
equation
AX B
111 x 2
230
y
5
.
121 z 1
Use a calculator to find the inverse of the coefficient matrix A and multiply both
sides of the equation by A
1
.
A
1
AX A
1
B
Therefore, the solution of the original system is x 7, y 3, z 2. ■
Only a matrix with the same number of rows as columns can possibly have an
inverse. Consequently, the method of Example 6 can be tried only when the sys-
tem has the same number of equations as unknowns. In this case, you should use
your calculator to verify that the coefficient matrix actually has an inverse (see the
Caution on page 812). If it does not, other methods must be used. Here is a sum-
mary of the possibilities.
SECTION 11.3 Matrix Methods for Square Systems 813
1.5 .5 1.5 1 1 1 x 1.5 .5 1.5 2
10 1
230
y
10 1
5
.5 .5 .5 1 2 1 z .5 .5 .5 1
100 x 1.5 .5 1.5 2
010
y
10 1
5
[Since A
1
A I
3
]
001 z .5 .5 .5 1
x 7
y
3
[Since I
3
X X]
z 2
Matrix Solution
of a System
of Equations
Suppose a system with the same number of equations as unknowns is writ-
ten in matrix form as AX B.
If the matrix A has an inverse, then the unique solution of the system is
X A
1
B.
If A does not have an inverse, then the system either has no solutions or has
infinitely many solutions. Its solutions (if any) may be found by using
Gauss-Jordan elimination (Section 11.2).

EXAMPLE 7
Solve the system
2x y z 2
x 3y 2z 1
x y z 2.
SOLUTION Since there are the same number of equations as unknowns, we
can try the method of Example 6. In this case, we have
2112
A
13 2
and B
1
.
11 1 2
APPLICATIONS
Just as two points determine a unique line, three points (that aren’t on the same
line) determine a unique parabola, as the next example demonstrates.
EXAMPLE 8
Find the equation of the parabola that passes through the points (1, 6), (3, 2),
and (4, 1).
SOLUTION As we saw in Section 4.1, a parabola is the graph of an equation
of the form
y ax
2
bx c
for some constants a, b, and c. Since (1, 6) is on the graph, we know that when
x 1, then y 6.
ax
2
bx c y
Let x 1 and y 6: a(1)
2
b(1) c 6
a b c 6. [Equation 1]
Similarly, since (3, 2) is on the graph, we have
ax
2
bx c y
Let x 3 and y 2: a(3
2
) b(3) c 2
9a 3b c 2. [Equation 2]
814 CHAPTER 11 Systems of Equations
Verify that the matrix A does have an inverse. Show that the solutions of the system
are x 2, y 1, z 1 by computing A
1
B.
CALCULATOR EXPLORATION
■

Finally, since (4, 1) is on the graph,
ax
2
bx c y
Let x 4 and y 1: a(4
2
) b(4) c 1
16a 4b c 1.
[Equation 3]
We can determine a, b, and c by solving the system determined by Equations 1–3.
a b c 6
9a 3b c 2
16a 4b c 1
or, in matrix form,
.
A calculator shows that the solution is
1
.
Using these values for a, b, and c, we obtain the equation of the parabola.
y ax
2
bx c
Let a 1, b 4, and c 1: y x
2
4x 1. ■
EXAMPLE 9
Matt Mahoney hits a baseball, and special measuring devices locate its position at
various times during its flight. If the path of the ball is drawn on a coordinate plane,
with the batter at the origin, it looks like Figure 11–27. According to the measuring
devices, the ball passes through the points (7, 9), (47, 38), and (136, 70).
(a) What is the equation of the path of the ball?
(b) How far from Matt does the ball hit the ground?
SOLUTION
(a) The path of the ball appears to be part of a parabola (a fact that will not be
proved here) and hence has an equation of the form
y ax
2
bx c.
As in Example 8, each of the points (7, 9), (47, 38) and (136, 70) determines
an equation.
(7, 9) a(7
2
) b(7) c 9
(47, 38): a(47
2
) b(47) c 38
(136, 70): a(136
2
) b(136) c 70.
1
4
1
6
2
1
1
1
1
1
3
4
1
9
16
a
b
c
6
2
1
a
b
c
1
1
1
1
3
4
1
9
16
SECTION 11.3 Matrix Methods for Square Systems 815
x
y
Figure 11–27
