Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


826
Chapter Outline
Interdependence of
Sections
12.1 Sequences and Sums
12.2 Arithmetic Sequences
12.3 Geometric Sequences
12.3.A Special Topics: Infinite Series
12.4 The Binomial Theorem
12.5 Mathematical Induction
This chapter deals with a variety of subjects involving counting processes
and the nonnegative integers 0, 1, 2, 3, . . . .
12.1 Sequences and Sums
■ Find terms of a sequence.
■ Write the formula for a sequence, given a few of its terms.
■ Find the formula for a recursively defined sequence.
■ Set up and solve applied problems using sequences.
■ Use summation notation.
■ Find partial sums of a sequence.
A sequence is an ordered list of numbers, such as
2, 4, 6, 8, 10, 12, . . .
1, 3, 5, 7, 9, 11, 13, . . .
1, 0, 1, 0, 1, 0, 1, 0, . . .
2, 1,
2
3
,
3
4
,
4
5
,
5
6
,
6
7
, . . . ,
where the dots indicate that the same pattern continues forever.* Each number on
the list is called a term of the sequence.
2, 1, 0, 1, 2, 3, 2, 1, 0, 1, 2, 3, 2, . . . .
1st 2nd 3rd 4th 5th 6th
term term term term term term
When the pattern isn’t obvious, as in the preceding examples, sequences are usu-
ally described in terms of a formula.
Section Objectives
12.2
12.1
12.4 12.3
12.5
Sections 12.1, 12.4, and 12.5 are
independent of one another and
may be read in any order.
*Such a list defines a function f whose domain is the set of positive integers. The rule is f (1)
first number on the list, f (2) second number on the list, and so on. Conversely, any function g whose
domain is the set of positive integers leads to an ordered list of numbers, namely, g(1), g(2), g(3), . . . .
So a sequence is formally defined to be a function whose domain is the set of positive integers.

EXAMPLE 1
(a) Find the first three terms of the sequence a
1
, a
2
, a
3
, . . . , a
n
, . . . where a
n
is
given by the formula
a
n
n
2
2
n
3
n
5
1
.
(b) Find a
39
.
SOLUTION
(a) To find a
1
, we substitute n 1 in the formula for a
n
; to find a
2
, we substitute
n 2 in the formula; and so on.
a
1
1
7
,
a
2
1
9
,
a
3
1
1
1
.
Thus, the sequence begins 1/7, 1/9, 1/11, . . . .
(b) The 39th term is
a
39
14
8
0
3
5
. ■
The subscript notation for sequences is sometimes abbreviated by writing
{a
n
} in place of a
1
, a
2
, a
3
, . . . .
EXAMPLE 2
Find the first three terms, the 41st term, and the 206th term of the sequence
n
(
1)
2
n
.
SOLUTION The formula is
a
n
n
(
1)
2
n
.
Substituting n 1, n 2, and n 3 shows that
a
1
1
(
1)
2
1
1
3
, a
2
2
(
1)
2
2
1
4
, a
3
(
3
1)
2
3
1
5
.
Similarly,
a
41
4
(
1
1
)
4
2
1
4
1
3
and a
206
2
(
06
1
)
20
2
6
2
1
08
. ■
39
2
3
39 1
2
39 5
3
2
3
3 1
2
3 5
2
2
3
2 1
2
2 5
1
2
3
1 1
2
1 5
SECTION 12.1 Sequences and Sums 827
EXAMPLE 3
Here are some other sequences whose nth term can be described by a formula.
Sequence nth Term First 5 Terms
a
1
, a
2
, a
3
, . . . a
n
n
2
1 2, 5, 10, 17, 26
b
1
, b
2
, b
3
, . . . b
n
1
n
1,
1
2
,
1
3
,
1
4
,
1
5
c
1
, c
2
, c
3
, . . . c
n
(n
(
1
1
)
)
n
(
n
1
2n
2)
1
3
,
1
3
,
1
3
0
,
1
4
5
,
2
5
1
x
1
, x
2
, x
3
, . . . x
n
3
1
1
0
n
3.1, 3.01, 3.001, 3.0001, 3.00001.
a
1
, a
2
, a
3
, . . . a
n
7 7, 7, 7, 7, 7. ■
A sequence in which every term is the same, such as the last one in Example
3, is called a constant sequence. A calculator is often useful for computing and
displaying the terms of more complicated sequences.
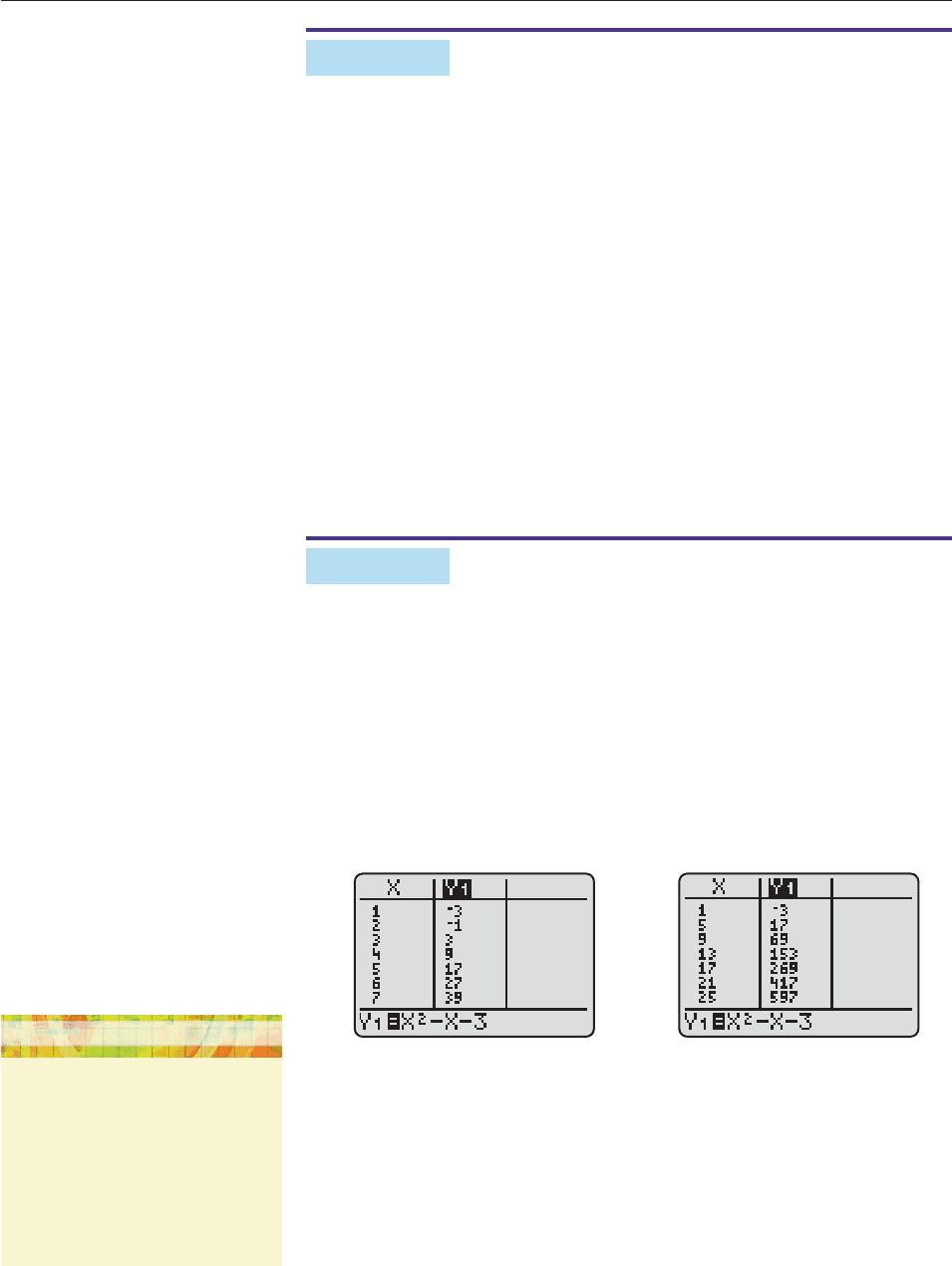
EXAMPLE 4
(a) Display the first five terms of the sequence {a
n
n
2
n 3} on your cal-
culator screen.
(b) Display the first, fifth, ninth, and thirteenth terms of this sequence.
SOLUTION
Method 1:
Enter the sequence in the function memory as y
1
x
2
x 3. In
the table set-up screen, begin the table at x 1 and set the increment at 1 and dis-
play a table of values (Figure 12–1). To display the first, fifth, ninth, and thirteenth
terms, set the table increment at 4 (Figure 12–2).
Figure 12–1 Figure 12–2
Method 2: Using the Technology Tip in the margin, enter the following, which
produces Figure 12–3 on the next page.
SEQ(x
2
x 3, x, 1, 5, 1).
To display the first, fifth, ninth and thirteenth terms, enter
SEQ(x
2
x 3, x, 1, 13, 4),
828 CHAPTER 12 Discrete Algebra
TECHNOLOGY TIP
SEQ (or MAKELIST on HP-39gs) is in
this menu/submenu:
TI-84/86: LIST/Ops
TI-89: MATH/List
Casio: OPTN/List
HP-39gs: MATH/List
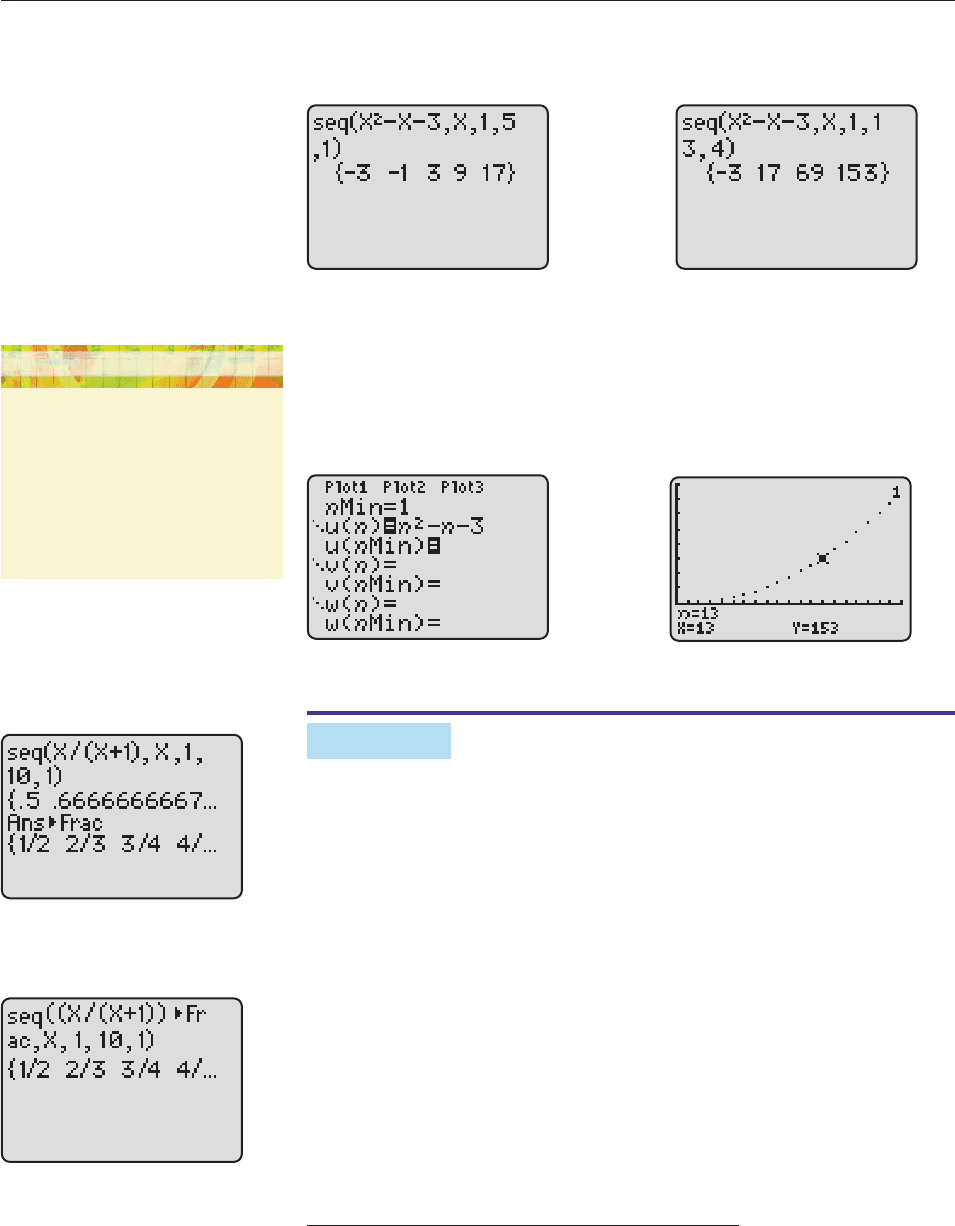
which tells the calculator to look at every fourth term from 1 to 13 and produces
Figure 12–4.
Figure 12–3 Figure 12–4
Method 3: If possible, put your calculator in sequence graphing mode (see
the Technology Tip in the margin). Enter the formula in the equation memory
(Figure 12–5). Now you can either construct a table (as in Method 1) or graph the
sequence and use the trace feature to determine its terms, as in Figure 12–6.* ■
Figure 12–5 Figure 12–6
EXAMPLE 5
Display the first ten terms of the sequence
n
n
1
on your calculator screen in
fractional form, if possible.
SOLUTION Creating a table always produces decimal approximations, as you
can easily verify. The same is usually true of the SEQ key, unless you take special
steps. On HP-39gs, change the number format mode to “fraction” (MODE menu).
On TI calculators (other than TI-89), either use the Frac key after obtaining the
sequence (Figure 12–7) or use parentheses and the Frac key as part of the func-
tion: Entering
SEQ(x/(x 1) 䉴Frac, x, 1, 10, 1)
produces Figure 12–8. In each figure, you must use the arrow key to scroll to the
right to see all the terms. ■
A sequence is said to be defined recursively (or inductively) if the first term
is given (or the first several terms) and there is a rule for determining the nth term
by using the terms that precede it.
400
20
0
SECTION 12.1 Sequences and Sums 829
*Set TI calculators for DOT instead of CONNECTED graphing in the MODE menu. This is not
necessary on Casio and not available on HP-39gs when it is in sequence mode.
Figure 12–7
Figure 12–8
TECHNOLOGY TIP
To change to sequence graphing mode,
choose SEQUENCE in this menu:
TI-84+/89: MODE
HP-39gs: APLET
On Casio, choose RECUR in the main
menu.

EXAMPLE 6
Consider the sequence whose first two terms are
a
1
1 and a
2
1
and whose nth term (for n 3) is the sum of the two preceding terms.
a
3
a
2
a
1
1 1 2,
a
4
a
3
a
2
2 1 3,
a
5
a
4
a
3
3 2 5.
For each integer n, the two preceding integers are n 1 and n 2. So
a
n
a
n1
a
n2
(n 3).
This sequence 1, 1, 2, 3, 5, 8, 13, . . . is called the Fibonacci sequence, and
the numbers that appear in it are called Fibonacci numbers. Fibonacci numbers
have many surprising and interesting properties, and are often found in nature.
See Exercises 76–82 for details. ■
EXAMPLE 7
The sequence given by
a
1
7 and a
n
a
n1
3 for n 2
is defined recursively. Its first three terms are
a
1
7, a
2
a
1
3 7 3 4,
a
3
a
2
3 4 3 1. ■
Entering a recursively defined sequence in a calculator (in sequence mode)
may require the use of special keys; check your instruction manual. Figure 12–9
shows the Fibonacci sequence in the function memory of a TI-84; the entry
“u(nMin) {1, 1}” indicates that the first two terms of the sequence are 1, 1. On
other calculators, these terms are entered directly as a
1
and a
2
, either in the func-
tion memory (HP-39gs) or in the RANG menu (Casio).
Sometimes, it is convenient or more natural to begin numbering the terms
of a sequence with a number other than 1. So we may consider sequences
such as
b
4
, b
5
, b
6
, . . . or c
0
, c
1
, c
2
, . . . .
EXAMPLE 8
The sequence 4, 5, 6, 7, . . . can be conveniently described by saying b
n
n, with
n 4. In the brackets notation, we write {n}
n4
. Similarly, the sequence
2
0
, 2
1
, 2
2
, 2
3
, . . .
may be described as {2
n
}
n0
or by saying c
n
2
n
, with n 0. ■
830 CHAPTER 12 Discrete Algebra
Figure 12–9
EXAMPLE 9
To buy a car, Leslie borrows $14,000 at 7% annual interest. Her monthly payment
is $277.22 for 60 months.
(a) Find a formula for a recursively defined sequence {u
n
} such that u
n
is the bal-
ance due on the loan after the nth payment.
(b) Find the balance after 30 months.
SOLUTION With car loans and home mortgages, interest is computed monthly
on the unpaid balance. The monthly interest rate is understood to be one-twelfth
of the annual rate, that is, .07/12.
(a) Let u
0
14,000, the balance after 0 payments. When the first payment is
made, the loan balance is
$14,000 one month’s interest $14,000
.
1
0
2
7
(14,000).
Subtracting the first loan payment gives the balance after one month
(rounded to the nearest penny).
u
1
$14,000
.
1
0
2
7
(14,000) 277.22 $13,804.45.
Similarly,
u
n
u
n1
.
0
1
7
2
u
n1
277.22,
Balance after Balance after Interest nth payment
n payments n 1 payments on u
n1
which can be written as
u
n
1
.
1
0
2
7
u
n1
277.22.
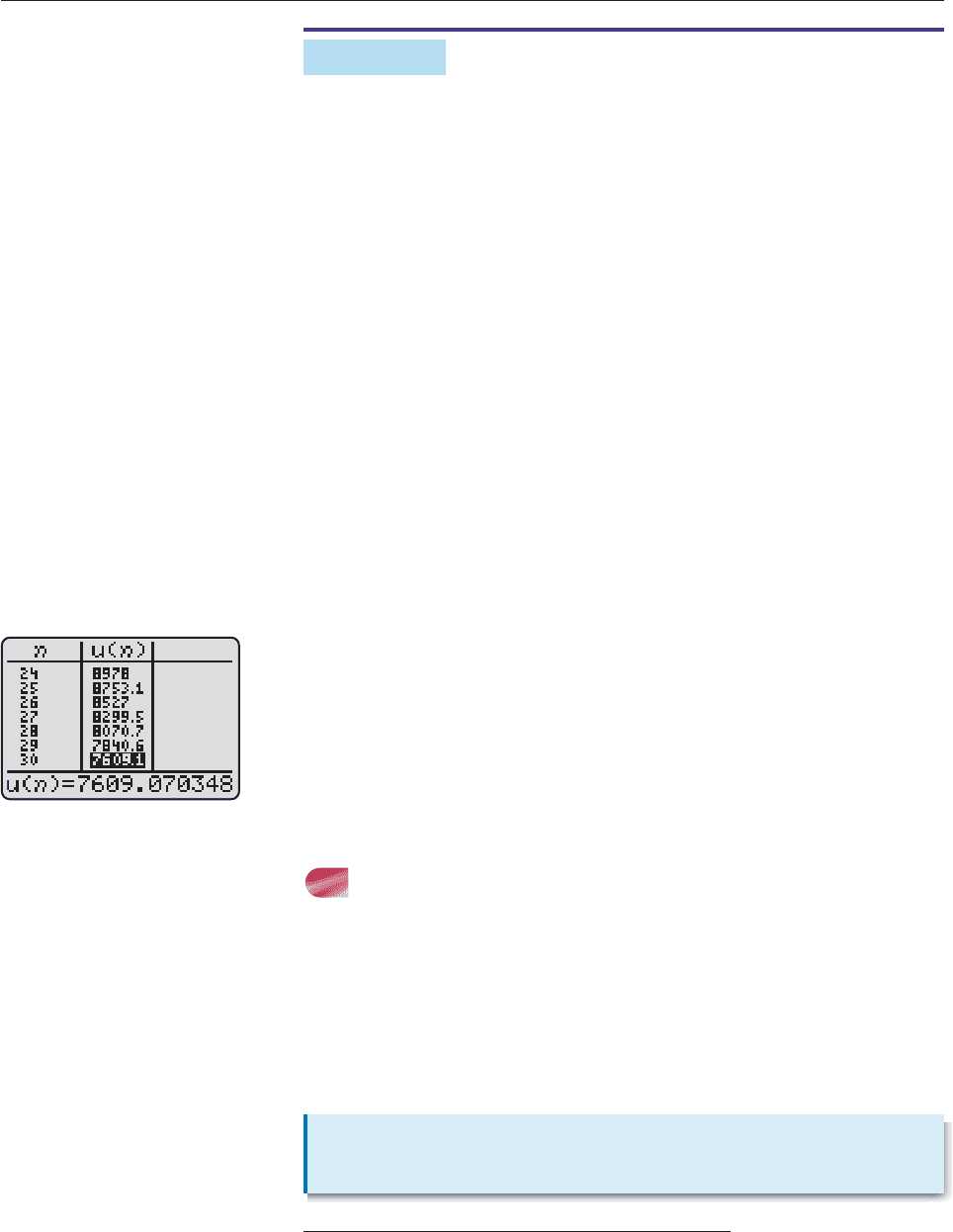
(b) Using the table feature of a calculator in sequence mode, we find that u
30
$7609.07, as shown in Figure 12–10. ■
SUMMATION NOTATION
It is sometimes necessary to find the sum of various terms in a sequence. For
instance, we might want to find the sum of the first nine terms of the sequence {a
n
}.
Mathematicians often use the Greek letter sigma () to abbreviate such a sum:*
9
k1
a
k
a
1
a
2
a
3
a
4
a
5
a
6
a
7
a
8
a
9
.
Similarly, for any positive integer m and numbers a
1
, a
2
, . . . , a
m
, we have the fol-
lowing.
SECTION 12.1 Sequences and Sums 831
——
—
—
—
Figure 12–10
* is the letter S in the Greek alphabet, the first letter in Sum.
Summation
Notation
m
k1
a
k
means a
1
a
2
a
3
a
m
.

An example of this situation is the sum 2
1
2
2
2
3
2
4
2
5
2
6
. To express
this sum in summation notation, you could let a
1
2
1
, a
2
2
2
, a
3
2
3
, a
4
2
4
,
a
5
2
5
, and a
6
2
6
, and write
6
k1
a
k
. However, since a
k
2
k
for each k, it is more
efficient to express this sum directly (without mentioning any a’s) as
6
k1
2
k
.
Conversely, if you are given a sum such as
5
k1
k
2
, you find the sum by
successively substituting k 1, 2, 3, 4, 5 for k in the expression k
2
and adding up
the result:
5
k1
k
2
1
2
2
2
3
2
4
2
5
2
55.
k 1 k 2 k 3 k 4 k 5
EXAMPLE 10
Compute each of these sums.
(a)
4
k1
k
2
(k 2) (b)
6
k1
(1)
k
k.
SOLUTION
(a) Successively substituting 1, 2, 3, 4 for k in k
2
(k 2) and adding the results,
we have
4
k1
k
2
(k 2) 1
2
(1 2) 2
2
(2 2) 3
2
(3 2) 4
2
(4 2)
1(1) 4(0) 9(1) 16(2) 40.
(b)
6
k1
(1)
k
k
(1)
1
1 (1)
2
2 (1)
3
3 (1)
4
4 (1)
5
5 (1)
6
6
1 2 3 4 5 6 3. ■
In sums such as
5
k1
k
2
and
6
k1
(1)
k
k, The letter k is called the summation
index. Any letter may be used for the summation index, just as the rule of a func-
tion f may be denoted by f (x) or f (t) or f (k). For example,
5
n1
n
2
means: Take the
sum of the terms n
2
as n takes values from 1 to 5. In other words,
5
n1
n
2
5
k1
k
2
.
Similarly,
4
k1
k
2
(k 2)
4
j1
j
2
( j 2)
4
n1
n
2
(n 2).
The
notation for sums can also be used for sums that don’t begin with
k 1. For instance,
10
k4
k
2
4
2
5
2
6
2
7
2
8
2
9
2
10
2
371
3
j0
j
2
(2j 5) 0
2
(2
0 5) 1
2
(2
1 5) 2
2
(2
2 5) 3
2
(2
3 5).
832 CHAPTER 12 Discrete Algebra
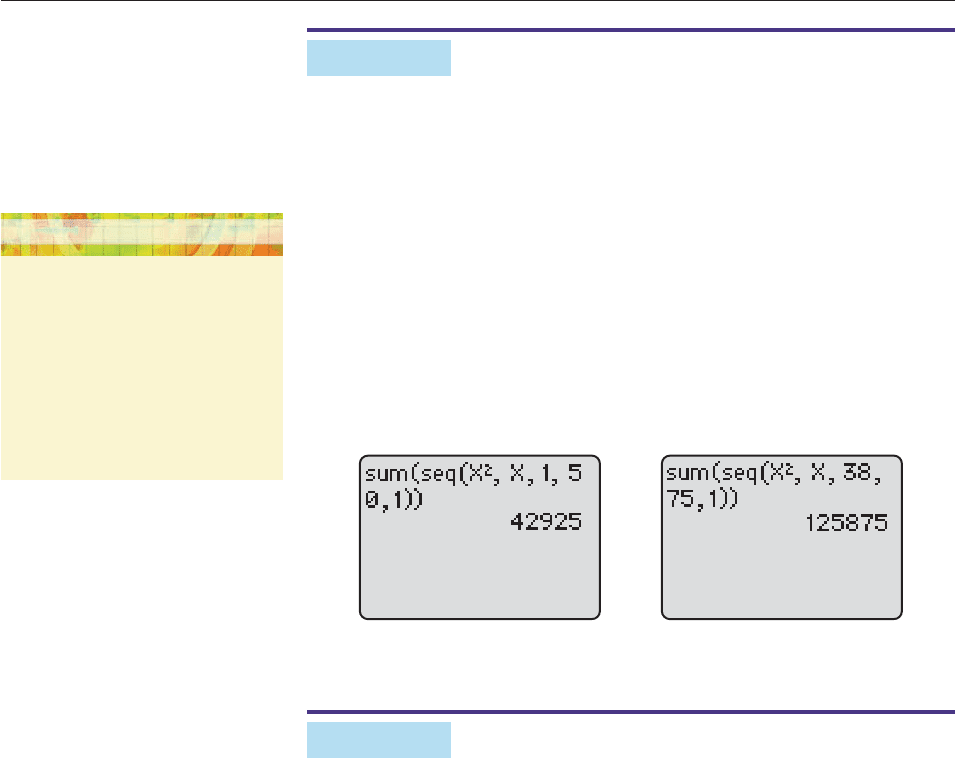
EXAMPLE 11
Use a calculator to compute these sums.
(a)
50
k1
k
2
(b)
75
k38
k
2
.
SOLUTION In each case, use SUM together with SEQ (or SLIST and MAKE-
LIST on HP-39gs), with the same syntax for SEQ as in Example 4:
50
k1
k
2
SUM SEQ(x
2
, x, 1, 50, 1) 42,925
and
75
k38
k
2
SUM SEQ(x
2
, x, 38, 75, 1) 125,875,
as shown in Figure 12–11. ■
Figure 12–11
EXAMPLE 12
Express the following sum in notation in two ways:
2l
1
n2
3l
1
n4
4l
1
n8
5ln
1
16
6ln
1
32
.
SOLUTION If we examine the pattern of the terms, we see that 2, 4, 8, 16, and
32 are powers of 2 and that the sum can be written as
2ln
1
2
1
3ln
1
2
2
4ln
1
2
3
5ln
1
2
4
6ln
1
2
5
.
In each denominator, the exponent of 2 is one less than the first term of the
denominator. Thus, when the first denominator term is k, the exponent is k 1
and each term of the sum has the form
k ln
1
2
k1
. Since the first term begins with
k 2 and k 1 1, we can write the sum as
2ln
1
2
1
3ln
1
2
2
4ln
1
2
3
5ln
1
2
4
6ln
1
2
5
6
k2
k ln
1
2
k1
.
For a second way to express this sum, we first write it as
(1 1
1
)ln2
1
(2 1
1
)ln2
2
(3 1
1
)ln2
3
(4 1
1
)ln2
4
(5 1
1
)ln2
5
.
(a) (b)
SECTION 12.1 Sequences and Sums 833
TECHNOLOGY TIP
SUM (or SLIST on HP-39gs) is in this
menu/submenu:
TI-84: LIST/Math
TI-86: LIST/Ops
TI-89: MATH/List
Casio: OPTN/List
HP-39gs: MATH/List

Now each term is of the form
(k 1
1
)ln2
k
, with k 1 corresponding to the first
term. So the sum can also be written as
2ln
1
2
1
3ln
1
2
2
4ln
1
2
3
5ln
1
2
4
6ln
1
2
5
5
k1
(k 1
1
)ln2
k
. ■
PARTIAL SUMS
Suppose {a
n
} is a sequence and k is a positive integer. The sum of the first k terms
of the sequence is called the kth partial sum of the sequence. Thus, we have the
following.
EXAMPLE 13
Here are some partial sums of the sequence {n
3
}:
First partial sum:
1
n1
n
3
1
3
1,
Second partial sum:
2
n1
n
3
1
3
2
3
9,
Sixth partial sum:
6
n1
n
3
1
3
2
3
3
3
4
3
5
3
6
3
441. ■
EXAMPLE 14
The sequence {2
n
}
n0
begins with the 0th term, so the fourth partial sum (the sum
of the first four terms) is
2
0
2
1
2
2
2
3
3
n0
2
n
.
Similarly, the fifth partial sum of the sequence
n(n
1
2)
n3
is the sum of the
first five terms.
3(3
1
2)
4(4
1
2)
5(5
1
2)
6(6
1
2)
7(7
1
2)
7
n3
n(n
1
2)
. ■
Certain calculations can be written very compactly in summation notation.
For example, the distributive law shows that
ca
1
ca
2
ca
3
ca
r
c(a
1
a
2
a
3
a
r
).
In summation notation, this becomes
r
n1
ca
n
c
r
n1
a
n
.
834 CHAPTER 12 Discrete Algebra
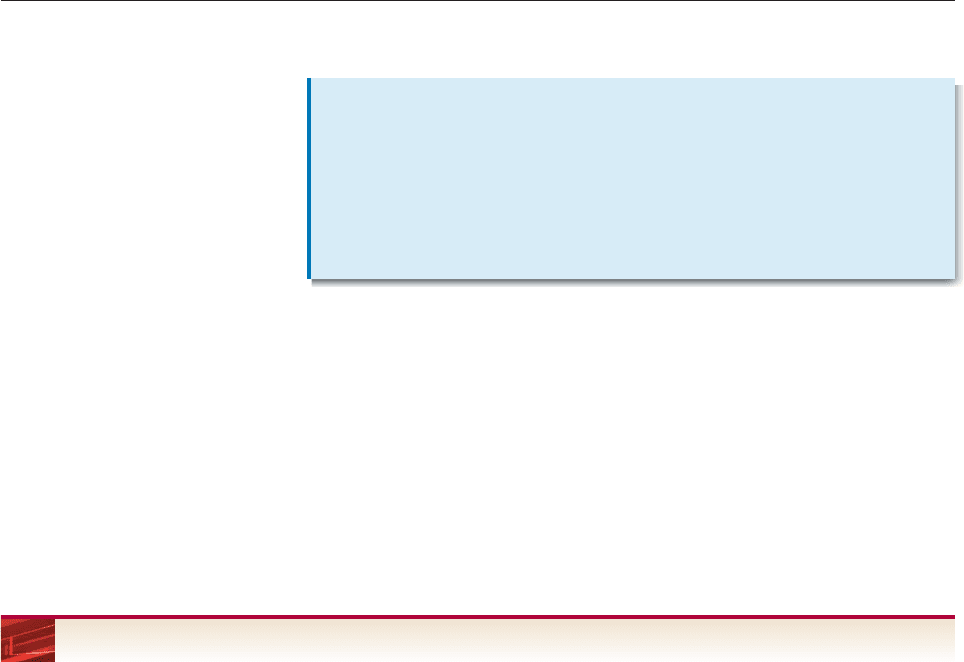
Partial
Sums
The kth partial sum of {a
n
} is
k
n1
a
n
a
1
a
2
a
3
a
k
.
This proves the first of the following statements.
To prove statement 2, use the commutative and associative laws repeatedly to
show that
(a
1
b
1
) (a
2
b
2
) (a
3
b
3
) (a
r
b
r
)
(a
1
a
2
a
3
a
r
) (b
1
b
2
b
3
b
r
),
which can be written in summation notation as
r
n1
(a
n
b
n
)
r
n1
a
n
r
n1
b
n
.
The last statement is proved similarly.
SECTION 12.1 Sequences and Sums 835
Properties
of Sums
1.
r
n1
ca
n
c
r
n1
a
n
for any number c.
2.
r
n1
(a
n
b
n
)
r
n1
a
n
r
n1
b
n
3.
r
n1
(a
n
b
n
)
r
n1
a
n
r
n1
b
n
EXERCISES 12.1
In Exercises 1–14, find the first five terms of the sequence
{a
n
}.
1. a
n
2n 6 2. a
n
2
n
7
3. a
n
n
1
3
4. a
n
(n 3)
1
(n 1)
5. a
n
2
n
n
6. a
n
n
2
1
7. a
n
(1)
n
n 2
8. a
n
(1)
n1
n(n 1)
9. a
n
4 (.1)
n
10. a
n
5 (.1)
n
11. a
n
(1)
n
3n 12. a
n
(1)
n2
(n 1)
13. a
n
is the nth digit in the decimal expansion of p.
14. a
n
is the nth digit in the decimal expansion of 1/13.
In Exercises 15–24, find a formula for the nth term of the
sequence whose first few terms are given.
15. 1, 1, 1, 1, 1, 1, . . .
16. 2, 2, 2, 2, 2, 2, . . .
17.
1
2
,
2
3
,
3
4
,
4
5
,
5
6
, . . .
18.
2
1
3
,
3
1
4
,
4
1
5
,
5
1
6
,
6
1
7
, . . .
19. 2, 7, 12, 17, 22, 27, . . .
20. 8, 5, 2, 1, 4, . . .
21. 3, 6, 12, 24, 48, . . .
22.
1
8
,
1
2
, 2, 8, 32, . . .
23. 4,
32,
48, 8,
80, . . .
24. 8, 5, 2, 11, 4, 17, 10, . . .
In Exercises 25–34, find the first five terms of the recursively
defined sequence.
25. a
1
4 and a
n
2a
n1
3 for n 2
26. a
1
0 and a
n
3a
n1
2 for n 2
27. a
1
16 and a
n
a
n
2
1
for n 2
28. a
1
3 and a
n
n 2a
n1
for n 2
29. a
1
2 and a
n
n a
n1
for n 2
30. a
1
3 and a
n
(1)
n
4a
n1
5 for n 2
31. a
1
1, a
2
2, a
3
3, and
a
n
a
n1
a
n2
a
n3
for n 4
32. a
1
1, a
2
3, and a
n
2a
n1
3a
n2
for n 3
33. a
0
2, a
1
3, and a
n
(a
n1
)
1
2
a
n2
for n 2
34. a
0
1, a
1
1, and a
n
na
n1
for n 2
