Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


which has a
1
20 and r e
.462
. Since e
.462
1, the series converges and its
sum is
1
a
1
r
1
2
e
0
.462
54.0573 mg.
So the amount levels off at approximately 54 mg. ■
We close this section by mentioning an alternative notation for infinite series.
The series
a
1
a
2
a
3
a
4
is denoted by
n1
a
n
.
For example,
n1
2(.6
n
) denotes the series
2(.6) 2(.6
2
) 2(.6
3
) 2(.6
4
) ,
and
n1
2
1
n
denotes
1
2
2
1
2
2
1
3
2
1
4
1
2
1
4
1
8
1
1
6
3
1
2
.
856 CHAPTER 12 Discrete Algebra
In Example 8(a) of Section 12.3, we saw that b
n
(the total amount in the bloodstream
after the nth dose) is given by
b
n
20
1
1
e
e
.4
.4
6
6
2
2
n
.
Confirm the answer in Example 5 by graphing the function f(x) 20
1
1
e
e
.
.
4
4
6
6
2
2
x
in the viewing window with 0 x 35 and 0 y 70. Use the trace feature to
show that as x gets larger and larger (more and more doses), y (total amount of
aminophylline) gets very close to 54.0573.
GRAPHING EXPLORATION
EXERCISES 12.3.A
In Exercises 1–8, find the sum of the infinite series, if it has
one.
1.
n1
2
1
n
2.
n1
3
4
n
3.
n1
(.06)
n
4. 1 .5 .25 .125 .0625
5. 500 200 80 32
6. 9 33
3 3
1
1
3
7. 2 2
1
1
2
1
2
8.
n1
2
1
n
3
1
n
In Exercises 9–15, express the repeating decimal as a rational
number.
9. .22222 10. .37373737
11. 5.4272727 12. 85.131313
13. 2.1425425425 14. 3.7165165165
15. 1.74241241241
16. If {a
n
} is an arithmetic sequence with common difference
d 0 and each a
i
0, explain why the infinite series
a
1
a
2
a
3
a
4
is not convergent.
17. (a) Verify that
n1
2(1.5)
n
is a geometric series with a
1
3
and r 1.5.

(b) Find the kth partial sum of the series and use this
expression to define a function f
, as in Example 2.
(c) Graph the function f in a viewing window with
0 x 30. As x gets very large, what happens to the
corresponding value of f(x)? Does the graph get closer
and closer to some horizontal line, as in Example 2?
What does this say about the convergence of the series?
18. Use the graphical approach illustrated in Example 2 to find
the sum of the series in Example 3. Does the graph get very
close to the horizontal line through 1/3? What’s going on?
In Exercises 19 and 20, use your calculator to compute partial
sums and estimate the sum of the convergent infinite series.
19.
p
2
(p
3
/
!
2)
3
(p
5
/
!
2)
5
(p
7
/
!
2)
7
, where n! is the
product 1
2
3
4
n.*
SECTION 12.4 The Binomial Theorem 857
20. 1 1
2
1
!
3
1
!
4
1
!
[Hint: What is the decimal
expansion of e?]
21. Find the steady state amount of aminophylline in the blood-
stream of the patient in Exercise 57 of Section 12.3. [See
Example 5 of this section.]
22. Find the steady state amount of cimetidine in the blood-
stream of the patient in Exercise 58 of Section 12.3.
12.4 The Binomial Theorem
■ Use the Binomial Theorem to expand binomial expressions.
■ Find terms of a binomial expansion.
The Binomial Theorem provides a formula for calculating the product (x y)
n
for
any positive integer n. Before we state the theorem, some preliminaries are
needed.
Let n be a positive integer. The symbol n! (read n factorial) denotes the prod-
uct of all the integers from 1 to n. For example,
2! 1
2 2, 3! 1
2
3 6, 4! 1
2
3
4 24,
5! 1
2
3
4
5 120,
10! 1
2
3
4
5
6
7
8
9
10 3,628,800.
In general, we have this result.
Learn to use your calculator to compute factorials. You will find ! in the Prob
(or Prb) submenu of the MATH or OPTN menu.
Section Objectives
n Factorial
Let n be a positive integer. Then
n! 1
2
3
4
(n 2)(n 1)n.
0! is defined to be the number 1.
15! is such a large number your calculator will switch to scientific notation to express
it. What is this approximation? Many calculators cannot compute factorials larger than
69! If yours does compute larger ones, how large a one can you compute without get-
ting an error message [or on HP-39gs, getting the number 9.9999
E499]?
CALCULATOR EXPLORATION
*See the n Factorial box below and the sentence immediately following it.

If r and n are integers with 0 r n, then we have the following.
For example,
5
C
3
5
3
3!(5
5
!
3)!
3!
5
2!
10,
4
C
2
4
2
2!(4
4
!
2)!
2
4
!2
!
!
6.
Binomial coefficients can be computed on a calculator by using
n
C
r
or Comb in
the Prob (or Prb) submenu of the MATH or OPTN menu.
The preceding examples illustrate a fact whose proof will be omitted: Every
binomial coefficient is an integer. Furthermore, for every nonnegative integer n,
n
0
1 and
n
n
1
because
n
0
0!(n
n
!
0)!
0
n
!n
!
!
n
n
!
!
1 and
n
n
n!(n
n
!
n)!
n
n
!0
!
!
n
n
!
!
1.
If we list the binomial coefficients for each value of n in this manner:
n 0
0
0
n 1
1
0
1
1
n 2
2
0
2
1
2
2
n 3
3
0
3
1
3
2
3
3
n 4
4
0
4
1
4
2
4
3
4
4
. ..
. ..
. ..
3
4
2
1
2
3
4
(1
2)(1
2)
4
5
2
1
2
3
4
5
(1
2
3)(1
2)
858 CHAPTER 12 Discrete Algebra
Binomial
Coefficients
n
Either of the symbols
or
n
C
r
denotes the number
r!(n
n
!
r)!
.
r
n
is called a binomial coefficient.
r
Although calculators cannot compute 475!, they can compute many binomial
coefficients, such as
4
4
7
0
5
0
, because most of the factors cancel out (as in the
previous example). Check yours. Will it also compute
4
1
7
0
5
0
?
CALCULATOR EXPLORATION

and then calculate each of them, we obtain the following array of numbers.
row 0 1
row 1 11
row 2 121
row 3 1331
row 4 14641
. ..
. ..
. ..
This array is called Pascal’s triangle. It has an interesting property:
Each interior entry of Pascal’s triangle is the sum of the
two closest entries in the row above it.
Two examples of this are shown above by the colored circles and arrows. Using
this fact we can easily construct row 5 of the triangle from row 4.
row 4: 14 64 1
row 5: 15101051
This property of Pacal’s triangle is proved in Exercise 69.
THE BINOMIAL THEOREM
To develop a formula for calculating (x y)
n
, we first calculate these products for
small values of n to see whether we can find some kind of pattern.
n 0(x y)
0
1
n 1(x y)
1
1x 1y
(
*
) n 2(x y)
2
1x
2
2xy 1y
2
n 3(x y)
3
1x
3
3x
2
y 3xy
2
1y
3
n 4(x y)
4
1x
4
4x
3
y 6x
2
y
2
4xy
3
1y
4
One pattern is immediately obvious: The coefficients shown in color above are
the top part of Pascal’s triangle! In the case n 4, for example, this means that the
coefficients are the numbers
14641
4
0
,
4
1
,
4
2
,
4
3
,
4
4
.
If this pattern holds for larger n, then the coefficients in the expansion of (x y)
n
are
n
0
,
n
1
,
n
2
,
n
3
, . . . ,
n
n 1
,
n
n
.
As for the xy-terms associated with each of these coefficients, look at the pattern
in (
*
) above: The exponent of x goes down by 1 and the exponent of y goes up by
1 as you go from term to term, which suggests that the terms of the expansion of
(x y)
n
(without the coefficients) are
x
n
, x
n1
y, x
n2
y
2
, x
n3
y
3
, . . . , xy
n1
, y
n
.
Combining the patterns of coefficients and xy-terms suggests that the follow-
ing result is true about the expansion of (x y)
n
.
SECTION 12.4 The Binomial Theorem 859
Using summation notation and the fact that
n
0
1
n
n
,
we can write the Binomial Theorem compactly as
(x y)
n
n
j0
n
j
x
nj
y
j
.
The Binomial Theorem will be proved in Section 12.5 by means of mathematical
induction. We shall assume its truth for now and illustrate some of its uses.
EXAMPLE 1
Expand (x y)
8
.
SOLUTION We apply the Binomial Theorem in the case n 8.
(x y)
8
x
8
8
1
x
7
y
8
2
x
6
y
2
8
3
x
5
y
3
8
4
x
4
y
4
8
5
x
3
y
5
8
6
x
2
y
6
8
7
xy
7
y
8
.
The coefficients can be computed individually by hand or by using
n
C
r
(or
COMB) on a calculator; for instance,
8
C
2
8
2
2
8
!6
!
!
28 and
8
C
3
8
3
3
8
!5
!
!
56.
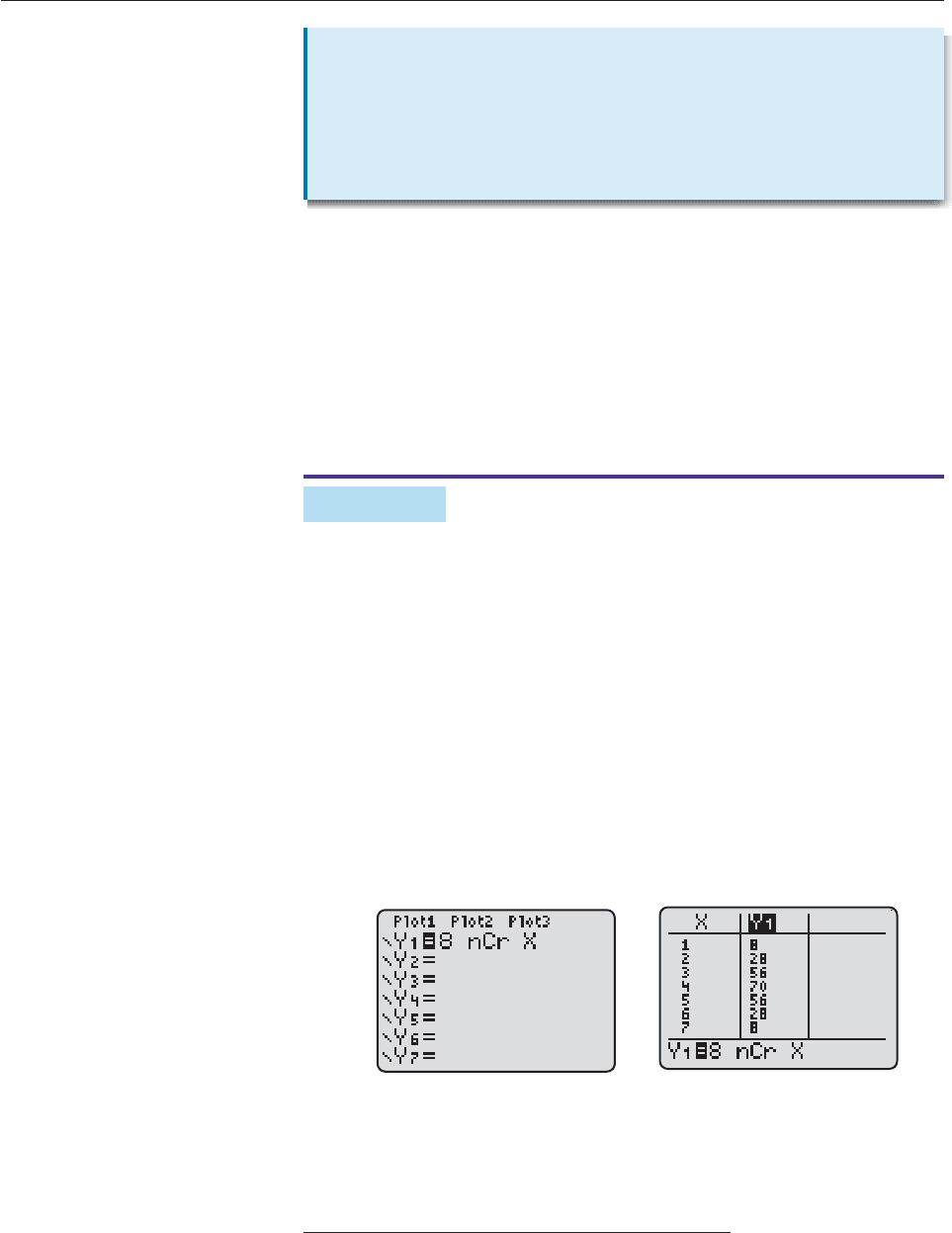
Alternatively, you can display all the coefficients at once by making a table of val-
ues for the function f (x)
8
C
x
, as shown in Figure 12–16.*
Figure 12–16
Substituting these values in the preceding expansion, we have
(x y)
8
x
8
8x
7
y 28x
6
y
2
56x
5
y
3
70x
4
y
4
56x
3
y
5
28x
2
y
6
8xy
7
y
8
. ■
860 CHAPTER 12 Discrete Algebra
The Binomial
Theorem
For each positive integer n,
(x y)
n
x
n
n
1
x
n1
y
n
2
x
n2
y
2
n
3
x
n3
y
3
n
n 1
xy
n1
y
n
.
*Thanks to Nick Goodbody for suggesting this method.
EXAMPLE 2
Expand (1 z)
6
.
SOLUTION Note that 1 z 1 (z) and apply the Binomial Theorem with
x 1, y z, and n 6.
(1 z)
6
1
6
6
1
1
5
(z)
6
2
1
4
(z)
2
6
3
1
3
(z)
3
6
4
1
2
(z)
4
6
5
1(z)
5
(z)
6
1
6
1
z
6
2
z
2
6
3
z
3
6
4
z
4
6
5
z
5
z
6
1 6z 15z
2
20z
3
15z
4
6z
5
z
6
. ■
EXAMPLE 3
If f (x) x
4
2x
3
5 and g(x) f (x 1), expand and simplify the rule of g.
SOLUTION The rule of g is found by replacing x by x 1 in the rule of f.
f (x) x
4
2x
3
5
g(x) f (x 1) (x 1)
4
2(x 1)
3
5.
Now we apply the Binomial Theorem to the terms (x 1)
4
and (x 1)
3
.
g(x) (x 1)
4
2(x 1)
3
5
(x
4
4x
3
6x
2
4x 1) 2(x
3
3x
2
3x 1) 5
x
4
4x
3
6x
2
4x 1 2x
3
6x
2
6x 2 5
x
4
6x
3
12x
2
10x 8. ■
EXAMPLE 4
Expand (x
2
x
1
)
4
.
SOLUTION Use the Binomial Theorem with x
2
in place of x and x
1
in place
of y.
(x
2
x
1
)
4
(x
2
)
4
4
1
(x
2
)
3
(x
1
)
4
2
(x
2
)
2
(x
1
)
2
4
3
(x
2
)(x
1
)
3
(x
1
)
4
x
8
4x
6
x
1
6x
4
x
2
4x
2
x
3
x
4
x
8
4x
5
6x
2
4x
1
x
4
. ■
Sometimes we need to know only one term in the expansion of (x y)
n
. If
you examine the expansion given by the Binomial Theorem, you will see that in
the second term y has exponent 1, in the third term y has exponent 2, and so on.
Thus, we have the following.
SECTION 12.4 The Binomial Theorem 861
TECHNOLOGY TIP
Binomial expansions, such as those in
Examples 1–4 can be done on TI–89.
Use Expand in the ALGEBRA menu.

For instance, in the ninth term of the expansion of (x y)
13
, y has exponent
8, the coefficient is
1
8
3
, and x must have exponent 5 (since 8 5 13). Thus,
the ninth term is
1
8
3
x
5
y
8
.
EXAMPLE 5
Find the ninth term of the expansion of
2x
2
4
6
y
13
.
SOLUTION We use the Binomial Theorem with n 13 and with 2x
2
in place
of x and
4
y
/6
in place of y. The remarks above show that the ninth term is
1
8
3
(2x
2
)
5
4
6
y
8
.
Since
4
y
y
1/4
and 6
3
2
3
1/2
2
1/2
, we can simplify as follows.
1
8
3
(2x
2
)
5
4
6
y
8
1
8
3
2
5
(x
2
)
5
(3
1/
(
2
y
)
1
8
/
(2
4
)
1
8
/2
)
8
1
8
3
2
5
x
10
3
4
y
2
2
4
1
8
3
3
2
4
x
10
y
2
3
2
4
x
10
y
2
28
9
6
x
10
y
2
. ■
13
12
11
10
9
5
4
3
2
862 CHAPTER 12 Discrete Algebra
Properties of the
Binomial Expansion
In the binomial expansion of (x y)
n
,
The exponent of y is always one less than the number of the term.
Furthermore, in each of the middle terms of the expansion,
The coefficient of the term containing y
r
is
n
r
.
The sum of the x exponent and the y exponent is n.
EXERCISES 12.4
In Exercises 1–18, evaluate the expression.
1. 6! 2. 10! 3.
8
6
!
!
4.
1
8
1
!
!
5.
9
1
!
2
3
!
!
6.
9!
7!
8!
7.
8.
9.
100
99
8
4
6
2
10.
11.
12.
13.
5
3
5
2
6
3
14.
1
1
2
1
1
1
1
0
7
0
15.
6
0
6
1
6
2
6
3
6
4
6
5
6
6
4
2
5
3
5
3
4
1
200
198

16.
6
0
6
1
6
2
6
3
6
4
6
5
6
6
17.
1
9
0
6
0
18.
7
7
5
2
In Exercises 19–38, expand and (where possible) simplify the
expression.
19. (x 1)
4
20. (x 1)
5
21. (x 2)
4
22. (x 2)
6
23. (x y)
5
24. (a b)
7
25. (a b)
5
26. (c d )
8
27. (2x y
2
)
5
28. (3u v
3
)
6
29. (x
1)
6
30. (2 y
)
5
31. (1 c)
10
32.
c
1
c
7
33. (x
3
x)
4
34. (3x
2
x
2
)
6
35. (1 3
)
4
(1 3
)
4
36. (3
1)
6
(3
1)
6
37. (1 i)
6
, where i
2
1
38. (2
i)
4
, where i
2
1
In Exercises 39–42, expand and simplify the rule of the
function g.
39. f (x) x
3
2x
2
x 4 and g(x) f (x 1)
40. f (x) 2x
3
3x
2
x and g(x) f (x 1)
41. f (x) x
4
3x 5 and g(x) f (x 2)
42. f (x) 2x
3
x 4 and g(x) f (x 3)
In Exercises 43–48, find the indicated term of the expansion of
the given expression.
43. third, (x y)
5
44. fourth, (a b)
6
45. fifth, (c d)
7
46. third, (a 2)
8
47. fourth,
u
2
u
2
7
48. fifth, (x
2
)
7
49. Find the coefficient of x
5
y
8
in the expansion of (2x y
2
)
9
.
50. Find the coefficient of x
12
y
6
in the expansion of (x
3
3y)
10
.
51. Find the coefficient of 1/x
3
in the expansion of
2x
x
1
2
6
.
52. Find the constant term in the expansion of
y
2
1
y
10
.
In Exercises 53–56, use the Binomial Theorem to factor the
expression.
53. x
5
5x
4
10x
3
10x
2
5x 1
54. x
4
4x
3
6x
2
4x 1
55. 16z
4
32z
3
24z
2
8z 1
56. 27y
3
27y
2
9y 1
SECTION 12.4 The Binomial Theorem 863
57. (a) Verify that
9
1
9 and
9
8
9.
(b) Prove that for each positive integer n,
n
1
n and
n
n
1
n. [Note: Part (a) is the case when n 9
and n 1 8.]
58. (a) Verify that
7
2
7
5
.
(b) Let r and n be integers with 0 r n. Prove that
n
r
n
n
r
. [Note: Part (a) is the case when n 7
and r 2.]
59. Prove that for any positive integer n,
2
n
n
0
n
1
n
2
n
n
.
[Hint: 2 1 1.]
60. Prove that for any positive integer n,
n
0
n
1
n
2
n
3
n
4
(1)
k
n
k
(1)
n
n
n
0.
61. Use the Binomial Theorem with y i sin u and x cos u to
find (cos u i sin u)
4
, where i
2
1.
62. (a) Use DeMoivre’s Theorem to find
(cos u i sin u)
4
.
(b) Use the fact that the two expressions obtained in part (a)
and in Exercise 61 must be equal to express cos 4u and
sin 4u in terms of sin u and cos u.
63. (a) Let f be the function given by f (x) x
5
. Let h be a
nonzero number and compute f (x h) f (x) (but
leave all binomial coefficients in the form
5
r
here
and below).
(b) Use part (a) to show that h is a factor of
f(x h) f(x) and find
f(x h
h
) f(x)
.
(c) If h is very close to 0, find a simple approximation of
the quantity
f(x h
h
) f(x)
. [See part (b).]
64. Do Exercise 63 with f(x) x
8
in place of f(x) x
5
.
65. Do Exercise 63 with f(x) x
12
in place of f(x) x
5
.
66. Let n be a fixed positive integer. Do Exercise 63 with
f(x) x
n
in place of f(x) x
5
.
67. Total credit card debt (in billions of dollars) in the United
States is approximated by
f (x) .052x
3
.7x
2
42.14x 213.4 (0 x 19)

where x 0 corresponds to 1990.* Suppose we want to
describe this situation by a function g, for which x 0
corresponds to 2000 instead of 1990.
(a) Explain why the function g(x) f (x 10) will work.
(b) How is the graph of g(x) related to the graph of f (x)?
[Hint: See Section 3.4.]
(c) Compute and simplify the rule of g(x).
68. According to data and projections in an article in USA
Today, the number of Internet phone calls (in millions) is
approximated by
f (x) .075x
3
.86x
2
3.66x 4(3 x 7),
where x 3 corresponds to 2003.
†
Write the rule of a func-
tion g(x), which provides the same information as f, but has
x 0 corresponding to 2003. [Hint: See Exercise 67.]
THINKERS
69. Let r and n be integers such that 0 r n.
(a) Verify that (n r)! (n r)[n (r 1)]!
(b) Verify that (n r)! [(n 1) (r 1)]!
864 CHAPTER 12 Discrete Algebra
(c) Prove that
r
n
1
n
r
n
r
1
1
for any r n 1.
[Hint: Write out the terms on the left side and use parts
(a) and (b) to express each of them as a fraction with
denominator (r 1)!(n r)!. Then add these two frac-
tions, simplify the numerator, and compare the result
with
n
r
1
1
.
(d) Use part (c) to explain why each entry in Pascal’s trian-
gle (except the 1’s at the beginning or end of a row) is the
sum of the two closest entries in the row above it.
70. (a) Find these numbers and write them one below the next:
11
0
, 11
1
, 11
2
, 11
3
, 11
4
.
(b) Compare the list in part (a) with rows 0 to 4 of Pascal’s
triangle. What’s the explanation?
(c) What can be said about 11
5
and row 5 of Pascal’s tri-
angle?
(d) Calculate all integer powers of 101 from 101
0
to 101
8
,
list the results one under the other, and compare the list
with rows 0 to 8 of Pascal’s triangle. What’s the expla-
nation? What happens with 101
9
?
71. Use the Binomial Theorem to show that 1.001
1000
2.
[Hint: Write 1.001 as a sum.]
*Federal Reserve.
†
November 28, 2003.
12.5 Mathematical Induction
■ Use mathematical induction.
Mathematical induction is a method of proof that can be used to prove a wide
variety of mathematical facts, including the Binomial Theorem, DeMoivre’s
Theorem, and statements such as the following.
The sum of the first n positive integers is the number
n(n
2
1)
.
2
n
n for every positive integer n.
For each positive integer n, 4 is a factor of 7
n
3
n
.
All of the preceding statements have a common property. For example, a
statement such as
The sum of the first n positive integers is the number
n(n
2
1)
or, in symbols,
1 2 3 n
n(n
2
1)
is really an infinite sequence of statements, one for each possible value of n.
n 1: 1
1(
2
2)
,
n 2: 1 2
2(
2
3)
,
n 3: 1 2 3
3(
2
4)
,
Section Objective

and so on. Obviously, there isn’t time enough to verify every one of the statements
on this list, one at a time. But we can find a workable method of proof by exam-
ining how each statement on the list is related to the next statement on the list.
For example, for n 50, the statement is
1 2 3 50
50(
2
51)
.
At the moment, we don’t know whether or not this statement is true. But just sup-
pose that it were true. What could then be said about the next statement, the one
for n 51?
1 2 3 50 51
51(
2
52)
.
Well, if it is true that
1 2 3 50
50(
2
51)
,
then adding 51 to both sides and simplifying the right side would yield these
equalities.
1 2 3 50 51
50(
2
51)
51,
1 2 3 50 51
50(
2
51)
2(5
2
1)
50(51)
2
2(51)
,
1 2 3 50 51
(50
2
2)51
,
1 2 3 50 51
51(
2
52)
.
Since this last equality is just the original statement for n 51, we conclude that
If the statement is true for n 50, then it is also true for n 51.
We have not proved that the statement actually is true for n 50, but only that if
it is, then it is also true for n 51.
We claim that this same conditional relationship holds for any two consecu-
tive values of n. In other words, we claim that for any positive integer k,
If the statement is true for n k, then it is also true for n k 1.
The proof of this claim is the same argument used earlier (with k and k 1 in
place of 50 and 51): If it is true that
1 2 3 k
k(k
2
1)
, [Original statement for n k]
then adding k 1 to both sides and simplifying the right side produces these
equalities.
1 2 3 k (k 1)
k(k
2
1)
(k 1),
1 2 3 k (k 1)
k(k
2
1)
2(k
2
1)
,
1 2 3 k (k 1)
(k 2)
2
(k 1)
,
1 2 3 k (k 1) .
[Original statement for n k 1]
(k 1)[(k 1) 1]
2
k(k 1) 2(k 1)
2
SECTION 12.5 Mathematical Induction 865
