Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


Chapter
12
Test
Sections 12.1–12.3; Special topics 12.3.A
1. Find the first five terms of the sequence {a
n
}, where
a
n
(1)
n2
(n 7).
2. The average cost of a dormitory room for one academic year
at a four-year public university is approximated by the arith-
metic sequence {b
n
}, where n 1 corresponds to the
2004–2005 school year and
b
n
185n 3227.*
(a) What was the cost in 2006–2007?
(b) If you begin attending a four-year public university in
2004–2005 and stay for six years (not uncommon),
what will the total cost of your dorm room be?
3. In the geometric sequence {c
n
}, c
5
2/3 and the common
ratio r 1/3.
(a) Find c
6
.
(b) Find the rule for c
n
.
4. Find the sum:
25
k1
(2k
2
4k 3).
5. Show that the sequence log 4, log 8, log 16, log 32,
log 64, . . . is arithmetic and find its common difference.
6. Show that the sequence {4
n4
} is geometric and find its
common ratio.
7. Find the first five terms of the sequence with
a
1
1, a
2
3, and a
n
2a
n1
3a
n2
for n 3.
8. Suppose b and c are constants. Show that the sequence
{9b 8cn} is arithmetic and find its common difference.
9. In the geometric sequence {a
n
}, a
2
10 and a
7
320.
(a) Find a formula for a
n
.
(b) Find a
5
.
10. Find the third and sixth partial sum of the sequence
{(2n 3n
2
)
2
}.
11. The arithmetic sequence {b
n
} has b
1
0 and b
8
34. Find
the 8
th
partial sum of the sequence.
12. The geometric sequence {c
n
} has c
2
9 and common ratio
r 1/2. Find the 7
th
partial sum and round your answer to
the nearest integer.
13. Express this sum in notation:
(2)
12
(2)
13
(2)
14
(2)
15
(2)
16
.
14. Find the sum:
40
n1
7
4
8n
.
15. A ball is dropped from a height of 10 feet. On each bounce,
it rises to 44% of the previous height. When it hits the
ground for the tenth time, how far has it traveled? Round
your answer to two decimal places.
16. The number of people living with AIDs in a given year is
approximated by the sequence {a
n
}, where n 1 corre-
sponds to 1998 and a
n
258,205(1.07)
n
.*
(a) How many people are living with AIDs in the years
2004 and 2007?
(b) If the sequence remains accurate, how many will be liv-
ing with AIDs in 2010?
17. Find the sum of all the integer multiples of 8 from 8 to 800.
18. Find the sum of the geometric series
1
2
1
1
0
5
1
0
2
1
50
.
Sections 12.4–12.5
19.
5
0
5
1
5
2
5
3
5
4
5
5
?
20. If f(x) x
6
x 1 and g(x) f(x 1), find and simplify
the rule of g(x).
21. Use mathematical induction to prove that for every positive
integer n,
10 12 14 2(n 4) n
2
9n.
22. Expand (4u v
3
)
6
.
23. Find the fifth term in the expansion of (
x
10
)
7
.
24. Prove that for every positive integer n, 4 is a factor of 5
n
3.
25. Prove that for each positive integer n,
n
1
n and
n
n
1
n.
26. Prove that for every positive integer n with n 3,
n
2
2n 1.
876 CHAPTER 12 Discrete Algebra
*Based on data from the U.S. National Center for Education Statistics.
*Based on estimates from the U.S. Centers for Disease Control and
Prevention.

877
DISCOVERY PROJECT 12 Taking Your Chances
Games of chance have been played in many societies throughout history, so it
should not be surprising that as mathematics becomes more sophisticated, its prin-
ciples are applied to the study of games of chance. Many common games can be
analyzed by using the techniques of discrete mathematics, particularly the Bino-
mial Theorem. The Binomial Theorem comes into play because of the nature of
gaming; each play is either a win or a loss, one of two choices. Consider the sim-
ple game of flipping a coin. What does a sequence of two games look like?
The tree diagram indicates four paths through the sequence of two games:
head-head, head-tail, tail-head, and tail-tail.
If you think of heads and tails as the variables H and T, then you have three
final results: H
2
, T
2
, and two HT’s if you consider HT TH. Indeed, you can
think of the last column of the tree as the polynomial of two variables
H
2
2HT T
2
.
The coefficients of the terms are the binomial coefficients you learned about in
the Binomial Theorem. You can use the theorem to help you describe many such
sequential games.
1. Write a polynomial that describes the results of a game in which you flip
a coin eight times in a row.
The variables H and T can also be used to represent the probability that you will
get heads or tails, respectively, when you flip a coin. If the coin you are using is a
fair one, then the probability of heads or tails is equally likely; that is, you would
expect to see heads half the time and tails half the time. These values of
1
2
are the
probabilities that heads or tails will appear on a given flip.
2. What is the probability that you will get exactly four heads and four tails
when you flip a coin eight times? Answer this by evaluating the H
4
T
4
term of the probability polynomial using the values H
1
2
and T
1
2
.
3. Show that the probability polynomial for flipping eight coins adds to
exactly 1.
T
T
T
TT
THH
H
H
HT
HH
Henryk T. Kaise r/Rex Instock/PictureQuest

878
DISCOVERY PROJECT 12
There is no magic to the values of
1
2
for winning or losing a game. The only
constraint is that the probability values for winning and losing must add to 1.
4. Suppose that you play a game in which the probability that you win is
0.47 and the probability that you lose is 0.53. What is the probability that
you win exactly four out of seven games? Evaluate the W
4
L
3
term of the
probability polynomial (W L)
7
.
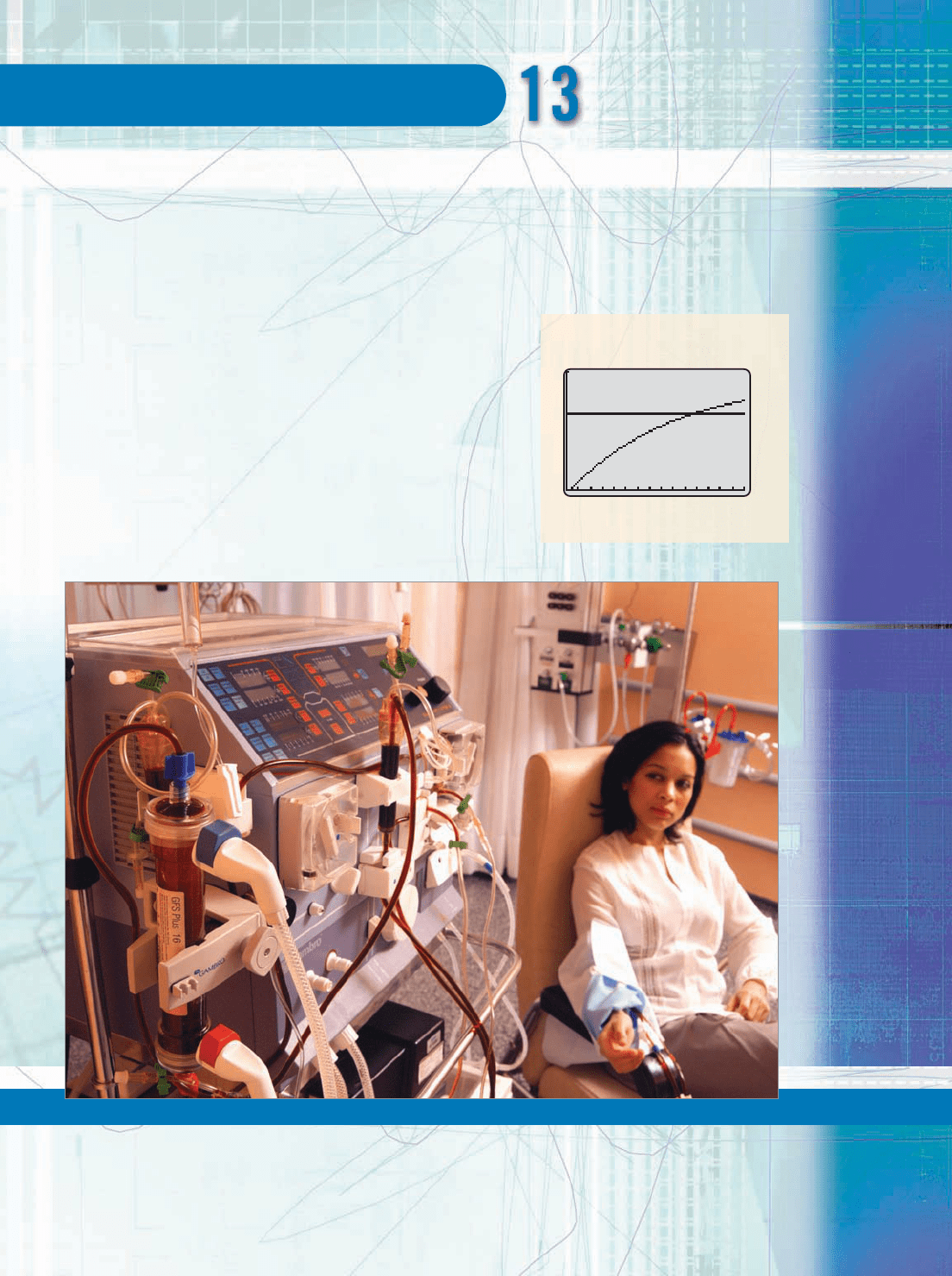
LIMITS AND CONTINUITY
Where did that number come from?
Doctors use a formula to determine when a dialysis
patient has been adequately dialyzed. Engineers
used a function to determine the shape of the
Gateway Arch in St. Louis. Economists and scientists
estimate the capacity of the earth to support its
population. Geologists and physicists compute the
amount of energy released by an earthquake. What
do these disparate formulas, functions, estimates,
and computations have in common? They all involve
e, a number that is given by a limit. See Exercise 50
on page 889 and Exercise 51 on page 923.
879
Chapter
© AJPhoto / Photo Researchers, Inc.
1
0
300
0

880
Chapter Outline
Interdependence of
Sections
13.1 Limits of Functions
13.2 Properties of Limits
13.2.A Special Topics: The Formal Definition of Limit
13.3 Continuity
13.4 Limits Involving Infinity
In earlier chapters, we dealt with static situations, such as the following:
What is the size of the angle?
How far did the rock fall?
How old is the skeleton?
Calculus, by contrast, deals with dynamic questions:
At what rate is the angle changing size?
How fast is the rock falling at time t 2 seconds?
What production rate will increase profits the most?
The key to dealing with such dynamic problems is the concept of limit,
which is introduced in this chapter.
13.1 Limits of Functions
■ Understand the informal definition of limit.
■ Use tables and graphs to find limits.
■ Identify situations in which a limit does not exist.
■ Find one-sided limits.
You have often dealt with questions such as this:
What is the value of the function f (x) when x 4?
Underlying the idea of “limit,” however, is the question:
How does the function f (x) behave near x 4?
EXAMPLE 1
The function
f (x)
is not defined at x 4 (why?). What happens to the values of f (x) when x is very
close to 4?
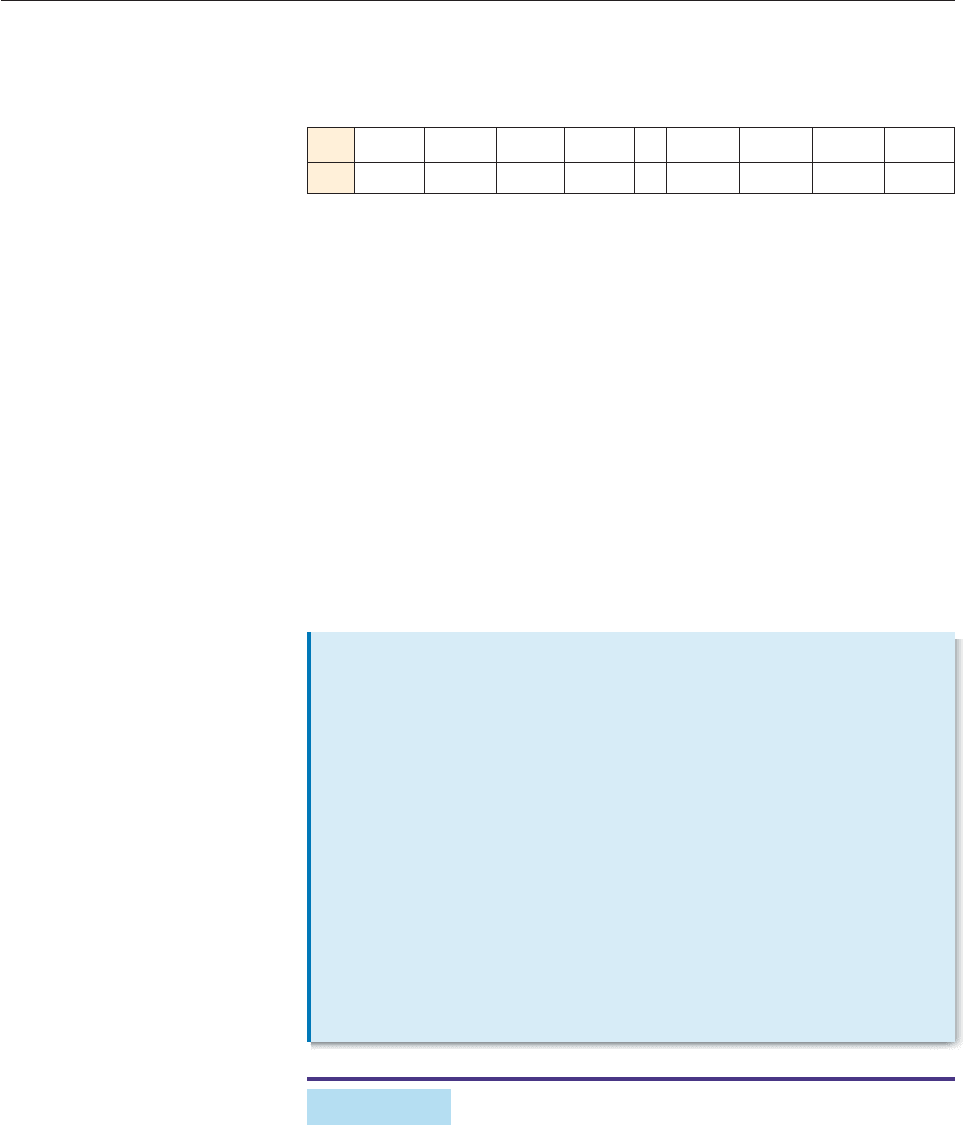
SOLUTION We evaluate f at several numbers that are very close to 4, includ-
ing numbers that are smaller than 4 and numbers that are larger than 4, that is,
.1x
4
.8x
3
1.6x
2
2x 8
x 4
13.3
13.1 13.2
13.4
Section Objectives
numbers that lie to the left of 4 and to the right of 4 on the number line, as shown
below.
x gets closer and closer to 4 from the left x gets closer and closer to 4 from the right
—————————————————————————————————————
The table suggests the following.
As x gets very close to 4 (from either side), the corresponding
values of f(x) get very close to 2.
Furthermore, by taking x close enough to 4, the corresponding values of f(x) can
be made as close as you want to 2. For instance,
f(3.999999) 1.999998 and f (4.000001) 2.000002.
This situation is usually expressed by saying that “the limit of f (x) as x approaches
4 is the number 2,” which is written symbolically as
lim
x4
f (x) 2orlim
x4
2. ■
Example 1 is an illustration of the following definition of “limit.” Now f is
any function, and c and L are fixed real numbers (in Example 1, c 4 and L 2).
The phrase “arbitrarily close” means “as close as you want.”
EXAMPLE 2
Find lim
x2
3x
2
.
SOLUTION In this case, f (x) 3x
2
. When x is a number very close to 2, then
x
2
is very close to 2
2 4. For instance,
x 1.9995 is very close to 2 and x
2
1.9995
2
3.99800025.
.1x
4
.8x
3
1.6x
2
2x 8
x 4
SECTION 13.1 Limits of Functions 881
Informal Definition
of Limit
Let f be a function, and let c be a real number such that f (x) is defined for
all values of x near x c, except possibly at x c itself. Suppose that
as x takes values very close (but not equal) to c (on both sides of c),
the corresponding values of f (x) are very close (and possibly equal)
to the real number L
and that
the values of f (x) can be made arbitrarily close to L for all
values of x that are sufficiently close (but not equal) to c.
Then we say that
the limit of the function f(x) as x approaches c is the number L,
which is written
lim
xc
f (x) L.
x 3.9 3.99 3.999 3.9999 4 4.0001 4.001 4.01 4.1
f(x) 1.8479 1.9841 1.9984 1.9998
*
2.0002 2.0016 2.0161 2.1681
Similarly, when x
2
is very close to 4, then 3x
2
is very close to 3
4 12. This
reasoning suggests that
lim
x2
3x
2
12.
The table in Figure 13–1 supports this conclusion (values of x close to 2 produce
values of f (x) 3x
2
close to 12). Furthermore, the limit of f as x approaches 2 is
the value of f at x 2 because f (2) 3(2
2
) 12. ■
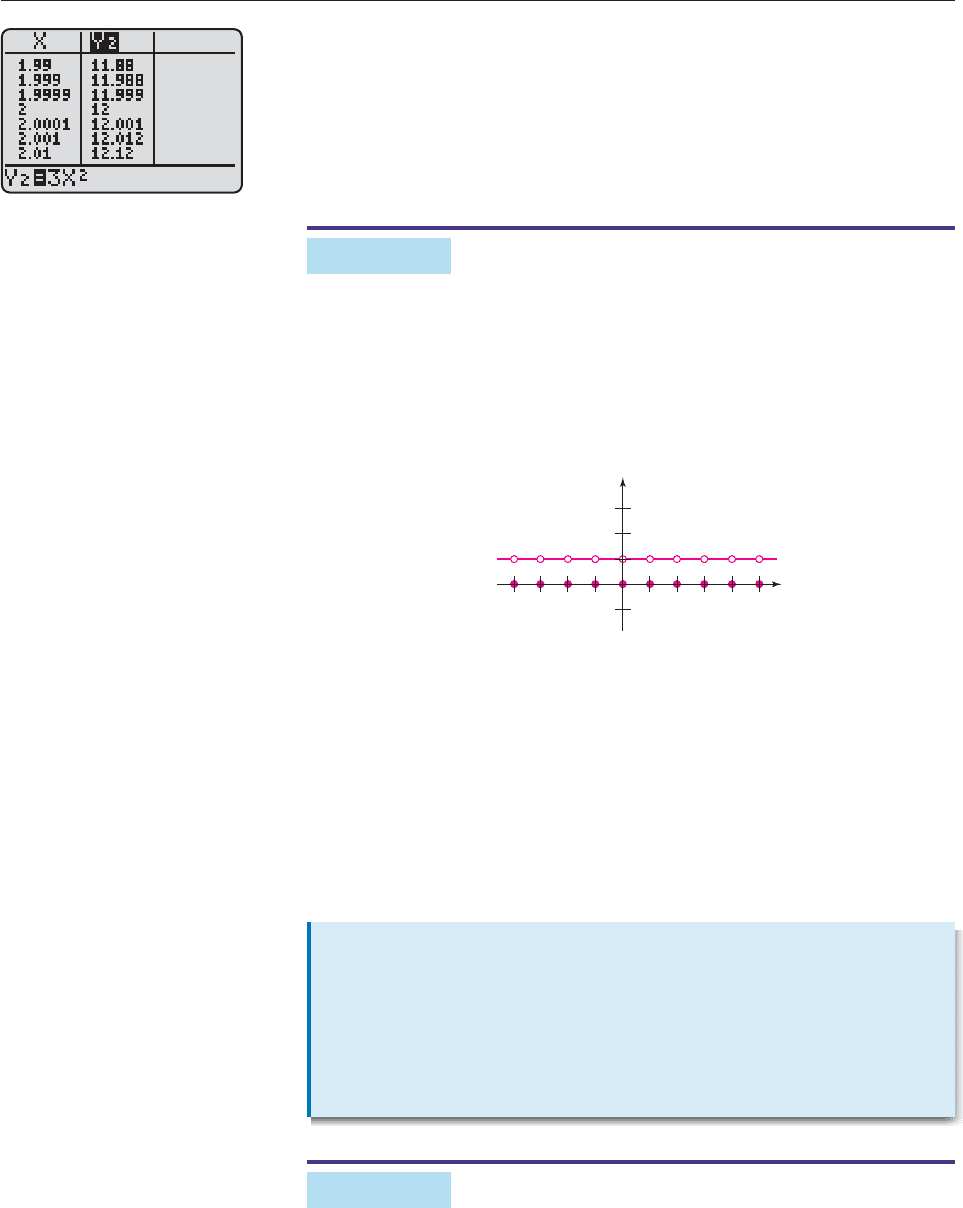
EXAMPLE 3
Find lim
x2
f (x), where f is the function given by this two-part rule:
0 if x is an integer,
f (x)
1 if x is not an integer.
SOLUTION A calculator is not much help here, but the function is easily
graphed by hand, as shown in Figure 13–2.
When x is a number very close (but not equal) to 2 (on either side of 2), the cor-
responding value of f (x) is the number 1, and this is true no matter how close x is
to 2. Thus,
lim
x2
f (x) 1.
Since f (2) 0 by definition, we see that the limit of f as x approaches 2 is not the
same as the value of the function f at x 2. ■
Examples 1–3 illustrate the following facts.
882 CHAPTER 13 Limits and Continuity
Figure 13–1
Limits and
Functional Values
If the function f (x) has a limit as x approaches c, then there are three possi-
bilities:
1. f (c) is not defined, but lim
xc
f (x) is defined. [Example 1]
2. f (c) is defined and lim
xc
f (x) f (c). [Example 2]
3. f (c) is defined, but lim
xc
f (x) f (c). [Example 3]
y
x
1 23−1−2
2
1
Figure 13–2
EXAMPLE 4
The graph of f (x)
sin
x
x
is shown in Figure 13–3. Find lim
x0
f (x).
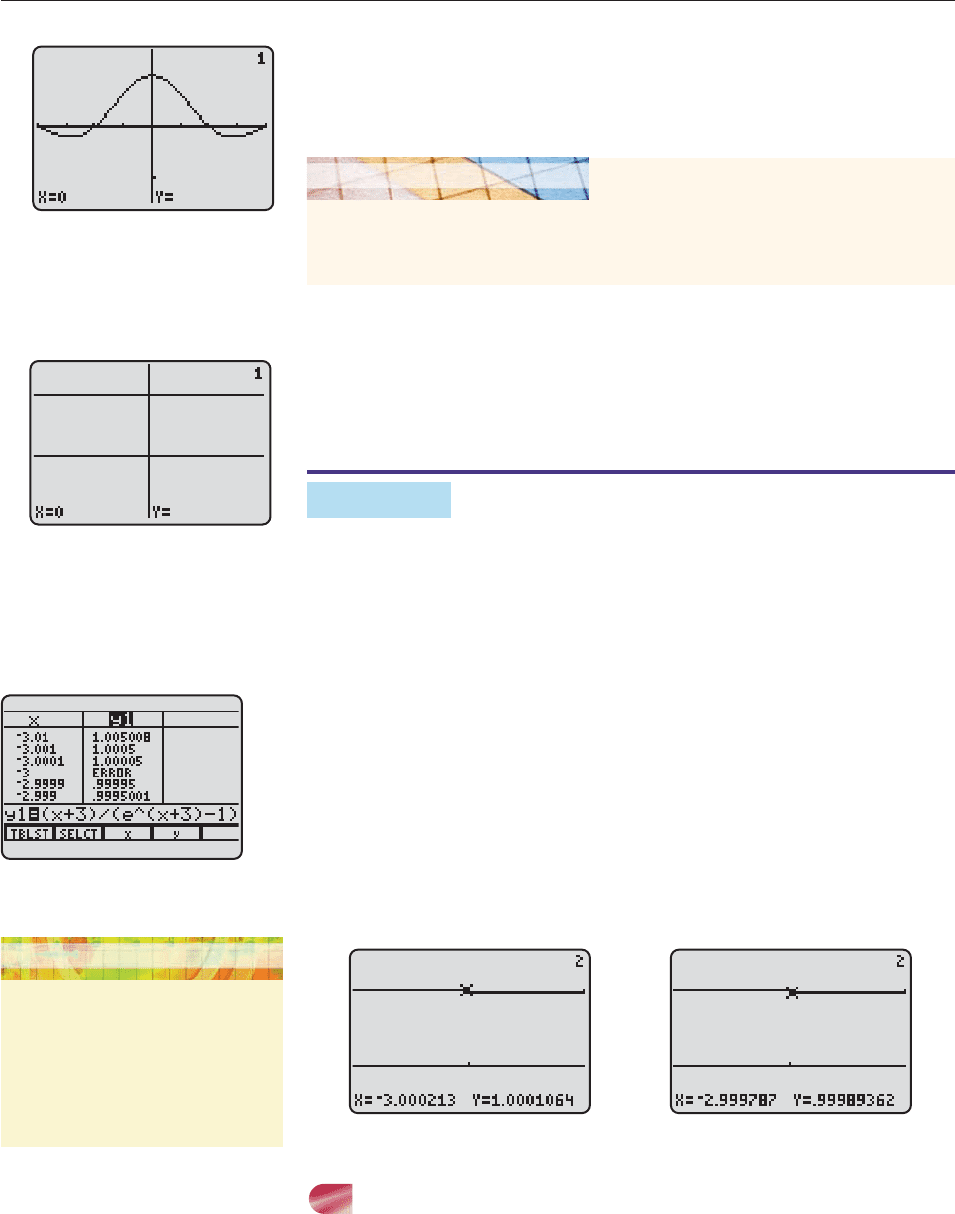
SOLUTION The function is not defined at x 0 (which is indicated by the
trace feature in Figure 13–3). To see what’s going on very close to x 0, we graph
f in the narrow viewing window of Figure 13–4, in which the graph looks like a
straight line.
The Graphing Exploration strongly suggests that
lim
x0
f (x) 1 or, equivalently, lim
x0
sin
x
x
1.
This is indeed the case, as will be proved in calculus. ■
EXAMPLE 5
Use numerical methods to find
lim
x3
e
x
x
3
3
1
.
Confirm your answer graphically.
SOLUTION Create a table of values for f (x)
e
x
x
3
3
1
when x is very close
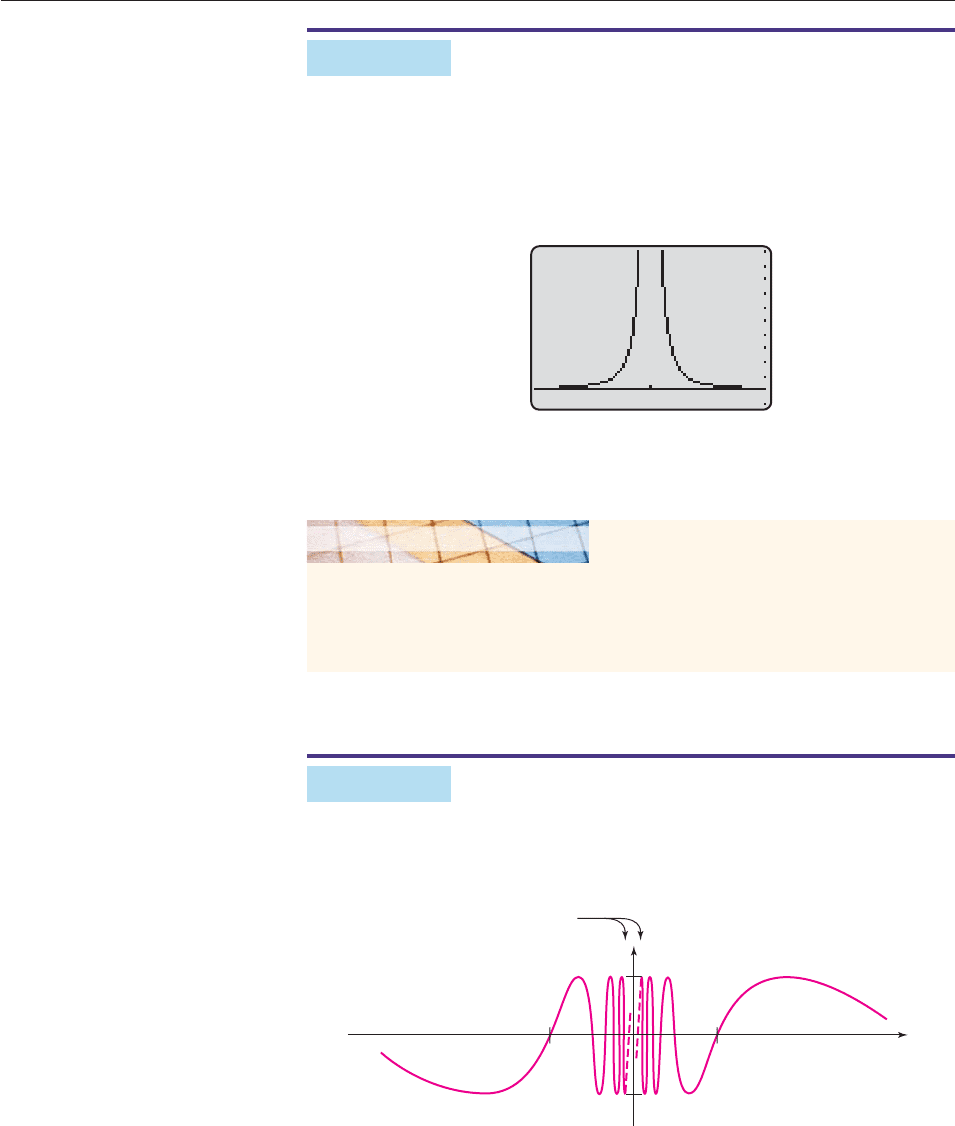
to 3, as in Figure 13–5 (which shows a TI-86 screen). The table indicates that f
is not defined when x 3. Nevertheless, the table suggests that
lim
x3
e
x
x
3
3
1
1.
We can confirm this conclusion by graphing f in a very narrow window around
x 3 and using the trace feature to examine the values of f (x) when x is very
close to 3. Figure 13–6 also suggests that the limit is 1. ■
Figure 13–6
NONEXISTENCE OF LIMITS
Not every function has a limit at every number. Limits can fail to exist for a vari-
ety of reasons, some of which are illustrated in the following examples.
SECTION 13.1 Limits of Functions 883
−1.5
1.5
−2π 2π
Figure 13–3
Graph f in the viewing window of Figure 13–4. Use the trace feature to move closer
and closer to the y-axis from both the left and the right, and note the values of f (x) as
x gets closer and closer to 0.
GRAPHING EXPLORATION
−1
1.5
−.1 .1
Figure 13–4
Figure 13–5
TECHNOLOGY TIP
To compute lim
xc
f (x) on TI-89, use
this syntax:
limit(f (x), x, c)
LIMIT is in the CALC menu on the TI-89
home screen.
EXAMPLE 6
Figure 13–7 shows the graph of
f (x)
(x
1
1)
2
.
Find lim
x1
f (x), if it exists.
SOLUTION
Therefore, the limit of f (x) as x approaches 1 does not exist. ■
EXAMPLE 7
As was explained in Example 6 on page 494, the graph of f(x) sin(p/x) oscil-
lates infinitely often between 1 and 1 as x approaches 0, as shown in Figure 13–8.
Figure 13–8
As x approaches 0, the function takes every value between 1 and 1 infinitely
many times. In particular, f (x) does not get closer and closer to one particular
number. Therefore, the limit of f (x) sin(p/x) as x approaches 0 does not exist.
■
Graph oscillates
infinitely often here
f(t) = sin (π/x)
1
−1
−11
x
y
884 CHAPTER 13 Limits and Continuity
Graph f (x) in the viewing window of Figure 13–7. Use the trace feature to show that
as x approaches 1 from the left or right, the corresponding values of f (x) become
larger and larger, without bound, rather than getting closer and closer to one particular
number.
GRAPHING EXPLORATION
−100
1000
−1.5 −.5
Figure 13–7

EXAMPLE 8
Find lim
x0
x
x
if it exists.
SOLUTION The function f (x) x/x is not defined when x 0. According
to the definition of absolute value, x x when x 0 and x x when
x 0. Therefore,
When x 0, then f (x)
x
x
x
x
1;
When x 0, then f (x)
x
x
x
x
1.
Consequently, the graph of f looks like Figure 13–9, as you can verify with a
calculator.
Figure 13–9
If x takes positive values closer and closer to 0, then the corresponding value of
f (x) is always 1. If x takes negative values closer and closer to 0, however, the cor-
responding value of f (x) is always 1. Thus, as x takes values close to 0 on both
sides of 0, as required by the definition of limit, the corresponding values of f (x)
do not get closer and closer to the same real number. Therefore, the limit does not
exist. ■
ONE-SIDED LIMITS
Although the limit does not exist in Example 8, we can adapt the limit concept to
describe the behavior of the function f (x)
x
x
near x 0. If you consider only
positive values of x, then the graph in Figure 13–9 shows that
as x takes values very close to 0 (with x 0), the corresponding
values of f (x) are very close (in fact, equal) to 1.
We express this fact by writing
lim
x0
f(x) 1
and saying
the limit of f (x) as x approaches 0 from the right is 1.
Similarly, if you consider only negative values of x, then
as x takes values very close to 0 (with x 0), the corresponding
values of f (x) are very close (in fact, equal) to 1.
y
x
1−1
−1
−2
2
1
SECTION 13.1 Limits of Functions 885
