Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


Therefore,
lim
h0
f (x h
h
) f (x)
lim
h0
x h
h
x
lim
h0
x
1
h
x
[Property 4]
[Constant Limits*]
[Property 5]
. [Polynomial Limit*] ■
Limits such as the one in Example 7 play a central role in calculus and have
a special name. The derivative of the function f, denoted f , is defined to be the
function whose rule is
f (x) lim
h0
f (x h
h
) f (x)
.
Example 7 shows that the derivative of f (x) x
is the function f given by
f (x)
2
1
x
.
1
2 x
1
x
x
1
lim
h0
(x
h)
x
1
lim
h0
x h
x
lim
h0
1
lim
h0
x h
lim
h0
x
896 CHAPTER 13 Limits and Continuity
*Remember that x is treated as a constant here. Hence, x h is a polynomial in h with constant term x.
EXERCISES 13.2
In Exercises 1–8, use the following facts about the functions
f, g, and h to find the required limit.
lim
x4
f(x) 5 lim
x4
g(x) 0 lim
x4
h(x) 2
1. lim
x4
( f (x) g(x)) 2. lim
x4
(g(x) h(x))
3. lim
x4
g
f (
(
x
x
)
)
4. lim
x4
g
h
(
(
x
x
)
)
5. lim
x4
f (x)g(x) 6. lim
x4
h(x)
2
7. lim
x4
2f (x
3
)
h
(x)
g(x)
8. lim
x4
f (x)
4
h(x
2
)
g(x)
In Exercises 9–40, find the limit if it exists. If the limit does not
exist, explain why.
9. lim
x2
(6x
3
2x
2
5x 3)
10. lim
x1
(x
7
2x
5
x
4
3x 4)
11. lim
x2
3
2
x
x
1
3
12. lim
x3
x
2
x
2
x
2
x
1
13. lim
x3
x
x
2
2
2
x
x
6
3
14. lim
x1
x
2
x
2
x
1
2
15. lim
x1
x
x
3
2
1
1
16. lim
x2
x
x
2
2
5
x
x
6
6
17. lim
x4
x
x
2
1
4
6
18. lim
x2
x
x
2
2
19. lim
x3
x
2
3
9
20. lim
x2
x
2
x
x
1
2
21. lim
x1
x
3
6
x
2
2
x 5
22. lim
x2
x
2
x
3
23. lim
x1
(x 1
3)
24. lim
x3
3
x
25. lim
x2.5
(5 2x
x)
26. lim
x3
(x 3
3x
) 27. lim
x3
x
x
3
3

28. lim
x25
x
x
25
5
29. lim
x0
1/(x 5
x
) 1/5
[Hint: Write the expression in
parentheses as a single fraction.]
30. lim
x0
2/(x 6
x
) 1/3
31. lim
x1
x
1
1
x
2
2
1
32. lim
x2
x
x
2
2
x
2
x
2
33. lim
x0
x
x
2
34. lim
x2
x 2
35. lim
x3
x
x
3
3
x 3
1
36. lim
x4
(
x 4
x
2
)
37. lim
x0
2 x
x
2
[Hint: Rationalize the numerator;
see Section 5.1.]
38. lim
x0
x x
1
1
1
x
39. lim
x0
x
x
x
x
40. lim
x3
x
x
3
3
In Exercises 41–44, find
lim
h0
f(2 h
h
) f(2)
.
41. f(x) x
2
42. f(x) x
3
SPECIAL TOPICS 13.2.A The Formal Definition of Limit 897
43. f (x) x
2
x 1 44. f (x) x
In Exercises 45 and 46, find lim
h0
f(0 h
h
) f(0)
, if it exists.
45. f(x) x 46. f (x) xx
In Exercises 47–50, find the rule of the derivative of the
function f. [See Example 7 and the remarks following it.]
47. f(x) 2x 3 48. f (x) 3x 5
49. f(x) x
2
x 50. f(x) x
2
x 1
In Exercises 51–54, find the rule of the derivative of the
function f. [The difference quotients of these functions were
found and simplified in Exercises 57–60 of Section 5.1.]
51. f (x) x 1
52. f (x) 2 x 3
53. f(x)
x
2
1
54. f (x)
x
2
x
55. Give an example of functions f and g and a number c such that
neither lim
xc
f (x) nor lim
xc
g(x) exists, but
lim
xc
( f (x) g(x)) does exist.
56. Give an example of functions f and g and a number c such
that neither lim
xc
f (x) nor lim
xc
g(x) exists, but lim
xc
f (x)g(x) does
exist.
■ Understand the formal definition of limit.
■ Prove statements about limits.
The informal definition of limit in Section 13.1 (or one very much like it) was
used for more than a century and played a crucial role in the development of cal-
culus. To avoid error, however, mathematical concepts such as limit must be
based on precise definitions and theorems. In this section, we take the first step
in building this rigorous foundation by developing the formal definition of
limit.
To keep the discussion as concrete as possible, suppose we have a function f
such that lim
x5
f (x) 12. You don’t need to know the rule of f or anything else about
it, except the informal definition of limit, to understand the following discussion.
The informal definition of the statement “lim
x5
f (x) 12” that was given in
Section 13.1 has two components:
A. As x takes values very close (but not equal) to 5, the corresponding val-
ues of f (x) are very close (and possibly equal) to 12.
B. The value of f (x) can be made arbitrarily close (as close as you want) to
12 for all x sufficiently close (but not equal) to 5.
13.2.A SPECIAL TOPICS The Formal Definition of Limit
Section Objectives
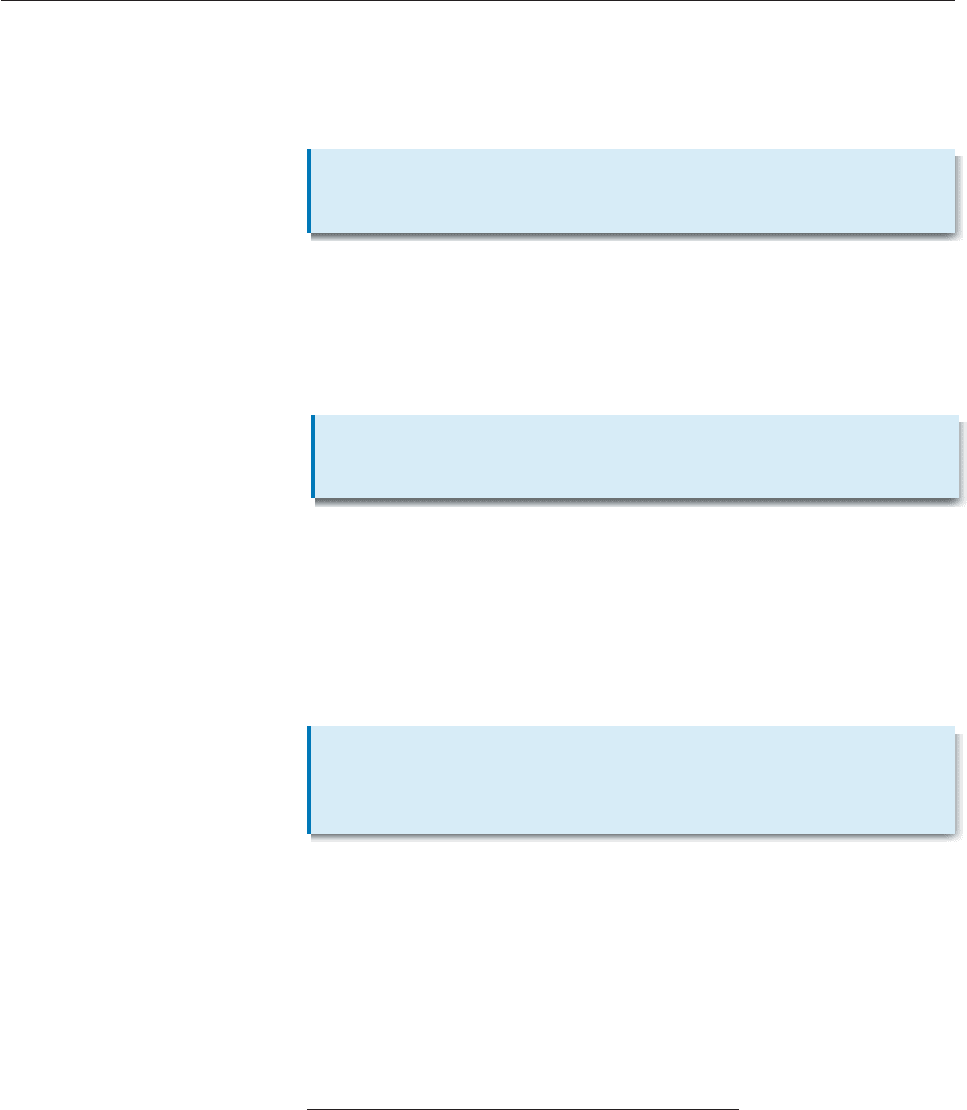
Strictly speaking, only component B is necessary, since it implies component A:
If the values of f (x) can be made arbitrarily close to 12 by taking x close enough
to 5, then it is certainly true that when x is very close to 5, f (x) must be very close
to 12.* Consequently, we begin with component B of the informal definition.
We shall modify this definition step by step until we reach the desired formal def-
inition.
Definition says, in effect, that a two-step process is involved: Whenever
you tell us how close you want f (x) to 12, we can tell you how close x must be to
5 to guarantee this. So it can be restated like this.
For example, if you want f (x) to be within .01 of 12 (that is, between 11.99 and
12.01), we must tell you how close x must be to 5 to guarantee that the correspon-
ding values of f (x) are between 11.99 and 12.01. But “arbitrarily close” implies
much more. We must be able to answer your demands, regardless of how close you
want f (x) to be to 12. If you want f (x) to be within .002 of 12, or within .0001 of
12, or within any distance of 12, we must be able to tell you how close x must be
to 5 in each case to accomplish this. So Definition can be restated as follows.
Hereafter, whatever small positive number you specify (measuring how close
f (x) should be to 12) will be denoted by the Greek letter e (epsilon).
†
When we tell
you how close x should be to 5 to accomplish this, we must give some small pos-
itive number that measures “how close” (for instance, x must be within .0003 of
5, or x must be within .00002 of 5). We denote the number that measures the close-
ness of x to 5 by the Greek letter d (delta).
‡
Presumably the number d, which
measures how close x must be to 5, will depend on the number e, which measures
how close you want f (x) to be to 12. In this language, Definition becomes the
following.
898 CHAPTER 13 Limits and Continuity
lim
x5
f (x) 12 means that the values of f (x) can be made as close as you want
to 12 for all x sufficiently close to 5.
lim
x5
f (x) 12 means that whenever you specify how close f (x) should be to
12, we can tell you how close x must be to 5 to guarantee this.
lim
x5
f (x) 12 means that no matter what positive number you specify
(measuring how close you want f (x) to 12), we can tell you how close x
must be to 5 to guarantee that f (x) is that close to 12.
*Component A was included in the informal definition because it describes the procedures that are
actually used to estimate a limit. In this case, we would compute values of f (x) when x 4.9, 4.99,
4.999, 5.1, 5.01, 5.001, etc. to see whether they are very close to 12.
†
Mathematicians have used Greek letters in this context since the formal definition was first developed
in the nineteenth century. Epsilon is the Greek letter e, the first letter in the word “error.” You can think
of e as measuring the allowable degree of error—the amount by which you will permit f (x) to differ
from 12.
‡
Delta is the Greek letter d, the first letter of “difference.” We must state the difference between x and
5 that will guarantee that f (x) is within e of 12.

Although Definition is essentially the formal definition, somewhat briefer
notation is usually used, as we now explain.
If we think of f(x) and 12 as numbers on the number line, then the statement
f (x) is within e of 12
means that
the distance from f (x) to 12 is less than e.
Since distance on the number line is measured by absolute value (see Section 1.1),
this last statement means
f (x) 12 e.
Similarly, saying that x is within d of 5 and not equal to 5 means that the distance
from x to 5 is less than d but greater than 0, that is,
0 x 5 d.
In this notation, Definition becomes the desired formal definition.
Definition is sufficiently rigorous because the imprecise terms such as
“arbitrarily close” and “sufficiently close” in the informal definition have been
replaced by a precise statement about inequalities that can be verified in specific
cases, as will be shown in the examples below. There is nothing special about
5 and 12 in the preceding discussion; the entire analysis applies equally well in the
general case and leads to this formal definition of limit (which is just Definition
with c in place of 5, L in place of 12, and f any function).
SPECIAL TOPICS 13.2.A The Formal Definition of Limit 899
lim
x5
f (x) 12 means that for every positive number e, there is a positive
number d (depending on e) with this property:
If x is within d of 5 (but not equal to 5), then f (x)
is within e of 12 (and possibly equal to 12).
lim
x5
f (x) 12 means that for each positive number e, there is a positive
number d (depending on e) with this property:
If 0 x 5 d, then f (x) 12 e.
Definition
of Limit
Let f be a function and let c be a real number such that f (x) is defined for
all x (except possibly x c) in some open interval containing c.* We say
“the limit of f (x), as x approaches c,isL” and write
lim
xc
f (x) L,
provided that for each positive number e, there is a positive number d
(depending on e) with this property:
If 0 x c d, then f (x) L e.
*This means that there are numbers a and b with a c b such that f (x) is defined for all x with
a x b, except possibly x c.

EXAMPLE 1
Let f (x) 4x 8, and prove that lim
x5
f (x) 12.
SOLUTION We must apply the definition of limit with c 5, L 12, and
f (x) 4x 8. Suppose that e is any positive number. We must find a positive
number d with this property.
If 0 x 5 d, then f (x) 12 e.
Let d be the number e/4; we claim that this d will work. For now, don’t worry
about how we figured out that d e/4 will work; just verify that the following
argument is valid: If x 5 d, then
x 5 e/4 [Since d e/4]
4x 5 e [Both sides multiplied by 4]
4x 5 e [Since 4 4]
4(x 5) e. [Property 4 of absolute value (page 10)]
4x 20 e
(4x 8) 12 e [Rewrite 20 as 8 12]
f (x) 12 e. [Because f (x) 4x 8]
We have verified that for each positive e, there is a positive d (namely, e/4) with
this property:
If 0 x 5 d, then f (x) 12 e.
This completes the proof that lim
x5
f (x) 12. ■
Proofs like the one in Example 1 often seem mysterious to beginners.
Although they can follow the argument after the appropriate d has been
announced, they don’t see how anyone found that particular d in the first place. So
here’s an example that gives a somewhat fuller picture of the mental processes
that are used in proving statements about limits.
EXAMPLE 2
Prove that lim
x1
(2x 7) 9.
SOLUTION Scratch Work In this case, f (x) 2x 7, c 1, and L 9. Let
e be any positive number. We must find a d with this property.
If 0 x 1 d, then (2x 7) 9 e.
To get some idea which d might have this property, we work backwards. The
conclusion we want to reach, namely,
(2x 7) 9 e,
is equivalent to
2x 2 e,
900 CHAPTER 13 Limits and Continuity

which in turn is equivalent to each of these statements.
2(x 1) e
2x 1 e
2x 1 e
x 1 e/2.
When the conclusion is written this way, it suggests that number e/2 would be a
good choice for d.
Everything up to here has been “scratch work” (the similar scratch work was
not included in Example 1). Now we must give the actual proof.
Proof Given a positive number e, let d be the number e/2. If 0 x 1 d,
then
x 1 e/2
[Since d e/2]
2x 1 e [Both sides multiplied by 2]
2x 1 e [Since 2 2]
2(x 1) e [Property of absolute value]
2x 2 e
(2x 7) 9 e [Rewrite 2 as 7 9]
f (x) 9 e. [Since f (x) 2x 7]
Therefore, d e/2 has the required property, and the proof is complete. ■
Once we did some algebraic scratch work in Examples 1 and 2, the limit
proofs were relatively easy. In most cases, however, a more involved argument is
required. In fact, it can be quite difficult to prove directly from the definition, for
example, that
lim
x3
x
x
3
2
2
4
x
x
2
1
x
1
3
.
Fortunately, such complicated calculations can often be avoided by using the vari-
ous limit properties given in Section 13.2. Of course, these properties must first be
proved by using the definition. Surprisingly, these proofs are comparatively easy.
EXAMPLE 3
Let f and g be functions such that
lim
xc
f (x) L and lim
xc
g(x) M.
Prove that
lim
xc
( f (x) g(x)) L M.
SOLUTION Scratch Work If e is any positive number, we must find a posi-
tive d with this property:
If 0 x c d, then ( f (x) g(x)) (L M) e.
SPECIAL TOPICS 13.2.A The Formal Definition of Limit 901

We first note that by the triangle inequality (page 11),
( f (x) g(x)) (L M) ( f (x) L) (g(x) M)
f (x) L g(x) M.
If we can find a d with this property:
If 0 x c d, then f (x) L g(x) M e,
then the smaller quantity ( f (x) g(x)) (L M ) will also be less than e when
0 x c d. We can find such a d as follows.
Proof Let e be any positive number. Apply the definition of lim
xc
f (x) L with
e/2 in place of e. There is a positive number d
1
with the following property.
If 0 x c d
1
, then f (x) L e/2.
Similarly, by the definition of lim
xc
g(x) M with e/2 in place of e, there is a pos-
itive number d
2
with the following property.
If 0 x c d
2
, then g(x) M e/2.
Now let d be the smaller of the two numbers d
1
and d
2
, so that d d
1
and
d d
2
. Then if 0 x c d, we must have
0 x c d
1
and 0 x c d
2
,
and therefore,
f (x) L e/2 and g(x) M e/2.
Consequently, if 0 x c d, then
( f (x) g(x)) (L M) ( f (x) L) (g(x)) M)
f(x) L g(x) M
2
e
2
e
e.
Thus, we have shown that for any e 0, there is a d 0 with the following property.
If 0 x c d, then ( f (x) g(x)) (L M ) e.
Therefore, lim
xc
( f (x) g(x)) L M. ■
The proofs of the other limit properties and theorems of Section 13.2 are dealt
with in Exercise 15 and in calculus.
Finally, the formal definition of limit may easily be carried over to one-sided
limits by using the following fact (see Special Topics 4.6.A).
x c d exactly when d x c d,
which is equivalent to
x c d exactly when c d x c d.
Thus, the numbers between c and c d lie to the right of c, within distance d of
c, and the numbers between c d and c lie to the left of c, within distance d of c.
Consequently, the formal definition of right-hand limits can be obtained from
the definition above by replacing the phrase “if 0 x c d” by
“c x c d.” For a formal definition of left-hand limits, replace the phrase
“if 0 x c d” by “c d x c.”
902 CHAPTER 13 Limits and Continuity

SECTION 13.3 Continuity 903
EXERCISES 13.2.A
In Exercises 1–12, use the formal definition of limit to prove
the statement, as in Examples 1 and 2.
1. lim
x3
(3x 2) 7 2. lim
x1
(4x 2) 6
3. lim
x5
x 5 4. lim
x0
(x 2) 2
5. lim
x2
(6x 3) 15 6. lim
x7
(2x 19) 5
7. lim
x1
4 4 8. lim
x2
p p
9. lim
x4
(x 6) 2 10. lim
x1
(2x 7) 5
11. lim
x2
(2x 5) 1 12. lim
x3
(2x 4) 10
In Exercises 13 and 14, use the formal definition of limit to
prove the statement.
13. lim
x0
x
2
0 14. lim
x0
x
3
0
In Exercises 15 and 16, let f and g be functions such that
lim
xc
f (x) L and lim
xc
g(x) M.
15. Prove that lim
xc
( f (x) g(x)) L M.
16. If k is a constant, prove that lim
xc
kf(x) kL.
17. (a) Describe the graph of g(x) x sin
p
x
near the origin.
(b) Use the formal definition of limit to prove that
lim
x0
x sin
p
x
0.
18. Let f be the function defined by
0 if x is irrational
f (x)
.
x if x is rational
Use the formal definition of limit to prove that
lim
x0
f(x) 0.
13.3 Continuity
■ Understand the definition of continuity.
■ Show that a function is continuous at a point.
■ Explore continuity on an interval.
■ Learn the properties of continuous functions.
Let c be a real number in the domain of a function f. Intuitively speaking, the func-
tion f is continuous at x c if you can draw the graph of f at and near the point
(c, f (c)) without lifting your pencil from the paper. For example, each of the four
graphs in Figure 13–13 is the graph of a function that is continuous at x c.
Figure 13–13
(c, f(c))
y
x
c
(c, f(c))
y
x
c
(c, f(c))
y
x
c
(c, f(c))
y
x
c
Section Objectives

On the other hand, none of the functions whose graphs are shown in Fig-
ure 13–14 is continuous at x c. If you don’t believe it, just try to draw one of
these graphs near x c without lifting your pencil from the paper.
Figure 13–14
Our goal is to find an analytical description of continuity at a point that does
not depend on having the graph given in advance. So let us consider the two pos-
sibilities when a function is continuous at x c, as shown in Figure 13–15.
Figure 13–15
We begin with the case of an interior point.*
If the graph can be drawn around the point (c, f (c)) without lifting pencil from
paper, then at the very least, f (x) must be defined for x c and for x t when t is
any number near c. We can describe this more precisely by saying the following.
Although condition is necessary for f to be continuous at x c, this con-
dition by itself does not guarantee continuity. For instance, the functions whose
(c, f(c))
(c, f(c))
(c, f(c)) is an
endpoint of
the graph
(c, f(c)) is an
interior point of
the graph
(c, f(c))
(a)
c
y
x
(c, f(c))
(b)
c
y
x
(d)
c
(c)
c
y
x
y
x
904 CHAPTER 13 Limits and Continuity
*The endpoint case is considered on page 907.
f (x) is defined for all x in some open interval containing c. In other words,
there are numbers a and b with a c b such that f (x) is defined for all x
with a x b. In particular, f (c) is defined.
CAUTION
When a calculator graphs in
“connected” mode, it plots a number of
points and then connects them with
line segments to produce a curve. Thus,
a calculator assumes that the function
is continuous at every point it plots,
which sometimes results in faulty or
misleading graphs. For example, a
calculator may not show the hole in
graph (d) of Figure 13–14, or it may
insert a vertical line segment in graph
(b) at the point where the graph jumps.

graphs are shown in Figure 13–14(a) and 13–14(b) on the facing page, are defined
for all values of x near c but are not continuous at x c.
Consider Figure 13–16, which shows a typical function f that is continuous at
x c. The point (x, f (x)) represents the pencil point as it moves along the graph
near the point (c, f (c)).
Figure 13–16
Note that
Furthermore,
As shown in Figure 13–16, the distance from the point (x, f (x)) to the dashed
vertical line is the same as the distance from x to c on the x-axis. Similarly, the dis-
tance from the point (x, f(x)) to the dashed horizontal line is the same as the dis-
tance from f (x) to f (c) on the y-axis. Consequently, statements and mean that
as x takes values closer and closer to c (on both sides of c),
the corresponding values of f (x) get closer and closer to f (c)
and that
the values of f (x) can be made as close as you want
to f (c) for all x close enough to c.
This last statement, together with statement above, looks suspiciously like the
definition of limit (with f (c) in place of L) and suggests that the idea of “not lift-
ing the pencil” can be expressed mathematically by saying
y
x
cx
f(c)
(x, f(x))
(c, f(c))
f(x)
SECTION 13.3 Continuity 905
As the pencil point (x, f (x)) gets closer to the vertical line through x c
(from the left or the right), it also gets closer and closer to the horizontal
line through y f(c).
The pencil point (x, f (x)) can be brought as close as you want to the hori-
zontal line by moving it close enough to the vertical line.
lim
xc
f (x) f (c).
