Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

LIMITS AT INFINITY
The word “limit” has been used thus far to describe the behavior of a function f
when x is near a particular number c. Now we consider the behavior of a function
when x is very large or very small.
EXAMPLE 3
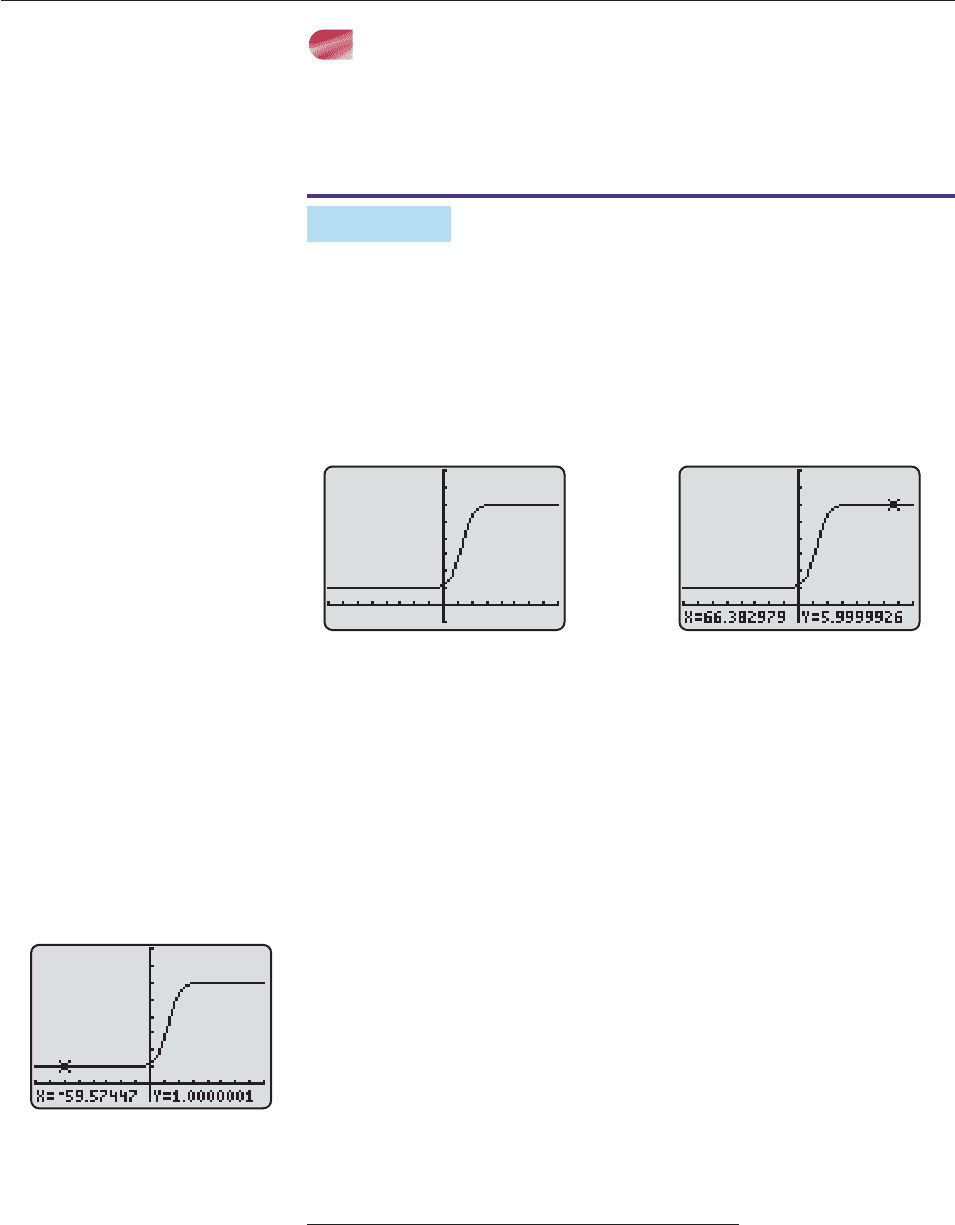
Figure 13–25 shows the graph of
f (x)
1 2
5
4e
x/4
1.
Describe the behavior of f when x is very large and when x is very small.
Figure 13–25 Figure 13–26
SOLUTION As you move to the right on the graph (that is, as x gets very large),
the graph gets very close to the horizontal line y 6, as shown in Figure 13–26.
In other words, as x gets larger and larger, the corresponding values of f (x) get
very close to 6. We express this fact symbolically by writing
lim
x
f (x) 6,
which is read “the limit of f (x) as x approaches infinity is the number 6.”
Toward the left, the graph gets very close to the horizontal line y 1. As x
gets smaller and smaller, the corresponding values of f (x) get very close to 1, as
shown in Figure 13–27.* We say that “the limit of f (x) as x approaches negative
infinity is 1” and write
lim
x
f (x) 1. ■
The limits illustrated in Example 3 are similar to those in Section 13.1 in that
the values of the function do approach a fixed number. The definition in the gen-
eral case is similar.
8
1
80
80
8
1
80
80
916 CHAPTER 13 Limits and Continuity
*Because of rounding off, the trace feature on most calculators will say that f(x) 1 when x is smaller
than approximately 60. However, the value of the function is always greater than 1 (why?).
8
1
80
80
Figure 13–27

This is an informal definition, as was the one in Section 13.1. Rigorous defi-
nitions (similar to those in Special Topics 13.2.A for ordinary limits) are discussed
in Exercises 49 and 50.
As Example 3 shows, limits as x approaches infinity or negative infinity cor-
respond to horizontal asymptotes of the graph of the function. Consequently, we
have this formal definition.
EXAMPLE 4
When x is a very large positive number, then 1/x is a positive number that is very
close to 0. Similarly, when x is a negative number that is large in absolute value
(such as 5,000,000), 1/x is a negative number that is very close to 0. These facts
suggest that
lim
x
1
x
0 and lim
x
1
x
0.
SECTION 13.4 Limits Involving Infinity 917
Limits
at Infinity
Let f be a function that is defined for all x a, for some number a. If
as x takes larger and larger positive values, increasing without
bound, the corresponding values of f (x) get very close (and possibly
equal) to the real number L
and
the values of f (x) can be made arbitrarily close (as close
as you want) to L for all large enough values of x,
then we say that
the limit of f (x) as x approaches infinity is L,
which is written
lim
x
f (x) L.
Similarly, if f is defined for all x b, for some number b, then
lim
x
f (x) L,
which is read
the limit of f (x) as x approaches negative infinity is L,
means that
as x takes smaller and smaller negative values, decreasing
without bound, the corresponding values of f (x) get very close
(and possibly equal) to the real number L,
and
the values of f (x) can be made arbitrarily close (as close
as you want) to L for all small enough values of x.
Horizontal
Asymptotes
The line y L is a horizontal asymptote of the graph of the function f if
either
lim
x
f (x) L or lim
x
f (x) L.
No polynomial function has a limit as x approaches infinity or negative
infinity, because no polynomial graph has a horizontal asymptote.
EXAMPLE 5
Describe the behavior of the polynomial function
f (x) x
3
10x 5
as x approaches infinity and as x approaches negative infinity.
SOLUTION Look what happens when x takes larger and larger positive values.
Thus, lim
x
f (x), in the sense defined on the preceding page, does not exist. Never-
theless, we can describe this situation by writing
lim
x
f (x) .
A similar situation occurs when x takes smaller and smaller negative values.
We describe this situation by writing
lim
x
f (x) . ■
PROPERTIES OF LIMITS AT INFINITY
The limits of constant functions are easily found. Consider, for example, the func-
tion f (x) 5. As x gets larger and larger (or smaller and smaller), the correspon-
ding value of f (x) is always the number 5, so that lim
x
f (x) 5 and lim
x
f (x) 5.
A similar argument works for any constant function.
918 CHAPTER 13 Limits and Continuity
Confirm that fact geometrically by graphing the function f (x) 1/x and verifying
that the x-axis (the horizontal line y 0) is a horizontal asymptote of the graph in
both directions.
■
GRAPHING EXPLORATION
Graph f (x) in the viewing window with
0 x 5000 and 0 y 100,000,000,000.
Use the trace feature to verify that as you move to the right along the graph, the
values of f (x) get larger and larger, increasing without bound.
GRAPHING EXPLORATION
Limit of
a Constant
If c is a constant, then
lim
x
c c and lim
x
c c.
GRAPHING EXPLORATION
Graph f (x) in the viewing window with 5000 x 0 and 100,000,000,000
y 0. Use the trace feature to verify that as you move to the left along the graph,
the values of f (x) get smaller and smaller, decreasing without bound.

Infinite limits have the same useful properties that ordinary limits have. For
instance, suppose that as x approaches infinity, the values of a function f get close
to a number L and the values of a function g get close to a number M. Then it is
plausible that the values of f (x) g(x) get close to L M, the values of f (x)g(x)
get close to L
M, and so forth. Similar remarks apply when x approaches nega-
tive infinity. More formally, we have the following.
SECTION 13.4 Limits Involving Infinity 919
Properties of
Limits at Infinity
If f and g are functions and L and M are numbers such that
lim
x
f (x) L and lim
x
g(x) M,
then
1. lim
x
( f (x) g(x)) L M;
2. lim
x
( f (x) g(x)) L M;
3. lim
x
( f (x)
g(x)) L
M;
4. lim
x
g
f (
(
x
x
)
)
M
L
; (provided that M 0)
5. lim
x
f (x)
L
. (provided that f (x) 0 for all large x)
Properties 1–5 also hold with in place of (provided that for property
5, f (x) 0 for all small x).
These properties are often stated somewhat differently. For example, since
lim
x
f (x) L and lim
x
g(x) M, Property 4 can be written as
lim
x
g
f (
(
x
x
)
)
l
l
i
i
m
x
m
x
g
f (
(
x
x
)
)
,
and similarly for the others.
If c is a constant, then Property 3 and Example 4 show that
lim
x
c
x
lim
x
c
1
x
(lim
x
c)
lim
x
1
x
c
0 0.
Repeatedly using Property 3 with this fact and Example 4, we see that for any
integer n 2,
lim
x
x
c
n
lim
x
c
x
1
x
1
x
1
x
lim
x
c
x
lim
x
1
x
lim
x
1
x
lim
x
1
x
0
0
0 0 0.
A similar argument works with in place of and produces this useful result.
Infinite
Limit Theorem
If c is a constant, then for each positive integer n,
lim
x
x
c
n
0 and lim
x
x
c
n
0.

This theorem and the limit properties above now make it possible to deter-
mine the limit (if it exists) of any rational function as x approaches infinity or neg-
ative infinity.
EXAMPLE 6
If you graph
f (x)
3
2
x
x
2
2
2
4
x
x
1
5
to the right of the y-axis, you will see that there appears to be a horizontal asymp-
tote close to y 1.5. We can confirm this fact algebraically by computing
lim
x
3
2
x
x
2
2
2
4
x
x
1
5
.
Property 4 cannot be used directly because neither the numerator nor the denom-
inator has a finite limit as x approaches infinity (see Example 5). So we first
divide both numerator and denominator by the highest power of x that appears,
namely, x
2
. When x 0, this does not change the value of the fraction, and we
have
lim
x
3
2
x
x
2
2
2
4
x
x
1
5
lim
x
lim
x
lim
x
[Property 4]
[Properties 1, 2]
[Limit of constant]
3
2
0
0
0
0
3
2
. [Limit Theorem] ■
3 lim
x
2
x
lim
x
x
1
2
2 lim
x
4
x
lim
x
x
5
2
lim
x
3 lim
x
2
x
lim
x
x
1
2
lim
x
2 lim
x
4
x
lim
x
x
5
2
lim
x
3
2
x
x
1
2
lim
x
2
4
x
x
5
2
3
2
x
x
1
2
2
4
x
x
5
2
3
x
x
2
2
2
x
x
2
x
1
2
2
x
x
2
2
4
x
x
2
x
5
2
3x
2
x
2
2
x 1
2x
2
x
4
2
x 5
920 CHAPTER 13 Limits and Continuity

The technique in Example 6 carries over to any rational function
f (x) g(x)/h(x), where g and h have the same degree, and provides the mathe-
matical justification for the treatment of horizontal asymptotes in Section 4.5 (see
Exercise 48). A slight variation of the procedure can be used to compute certain
limits involving square roots.
EXAMPLE 7
Find
(a) lim
x
2
3
x
x
2
3
1
(b) lim
x
2
3
x
x
2
3
1
SOLUTION
(a) We need only consider positive values of x. When x is positive,
x
2
x.
Therefore,
lim
x
2
3
x
x
2
3
1
lim
x
lim
x
lim
x
lim
x
[Property 4]
[Property 5]
[Property 1]
2
3
0
0
2
3
. [Constant limit and Limit Theorem]
lim
x
3
lim
x
x
1
2
lim
x
2 lim
x
3
x
lim
x
3
x
1
2
lim
x
2
3
x
lim
x
3
x
1
2
lim
x
2
3
x
3
x
1
2
2
3
x
3x
2
x
2
1
2x
x
3
3
x
2
x
2
1
2x
x
3
3x
x
2
1
2x
x
3
SECTION 13.4 Limits Involving Infinity 921
Graph the function in a viewing window with 500 x 500, and verify that
there appear to be two horizontal asymptotes, one below the x-axis to the left and
one above the x-axis to the right. Use the trace feature to estimate the required lim-
its. Compare your estimates to the results that we now obtain algebraically.
GRAPHING EXPLORATION
(b) To compute the limit as x approaches negative infinity, we need only consider
negative values of x and use the fact that when x is negative, x
x
2
(for instance, 2
(2)
2
). Then an argument similar to the one in part
(a) shows that
lim
x
2
3
. ■
3x
2
1
2x 3
922 CHAPTER 13 Limits and Continuity
EXERCISES 13.4
In Exercises 1–8, use a calculator to estimate the limit.
1. lim
x
[
x
2
1
(x 1)]
2. lim
x
[
x
2
x
1
x]
3. lim
x
x
2/3
x
3
x
4/3
4. lim
x
2
x
x
5/
4
x
5/
x
4
5. lim
x
sin
1
x
6. lim
x
sin
x
x
7. lim
x
ln
x
x
8. lim
x
1 (1.
5
1)
x/20
In Exercises 9–14, list the vertical asymptotes of the graph (if
there are any). Then use the graph of the function f to find
lim
x
f (x) and lim
x
f (x).
9.
10.
11.
y
x
20 6020 40
2
3
1
1
2
y
x
20 10301020
2
3
1
1
y
x
10 5 105
2
3
1
12.
13.
14.
In Exercises 15–20, use the Infinite Limit Theorem and the
properties of limits as in Example 6 to find the horizontal
asymptotes (if any) of the graph of the given function.
15. f (x)
4x
2
3x
2
6
x
5
2
16. g(x)
x
2
x
2
2
x 1
17. h(x)
2x
2
2
x
6
x
x
2
1
y
x
204060 601020
8
12
4
4
y
x
10301020
10
15
5
5
10
15
20
y
x
2040 6020 40
10
15
5
5
10
15

18. k(x)
2
3
x
x
x
x
3
2
x
4
2
19. f (x)
20. g(x)
In Exercises 21–39, use the Infinite Limit Theorem and the
properties of limits to find the limit.
21. lim
x
(x
2x
2
3)(
x
x
1
2)
22. lim
x
(2
3
x
x
2
1)
2
(3
x
x
5
2)
23. lim
x
3x
x
1
2
24. lim
x
(3x
2
1)
2
25. lim
x
x
3
x
2
x
2
x
1
26. lim
x
x
2
x
1
x
3
2x
2
x
27. lim
x
x
2
2x
2
x
28. lim
x
x
2
x
1
29. lim
x
3
2
x
x
2
2
1
30. lim
x
3
2
x
x
2
2
1
31. lim
x
3
2
x
x
2
5
1
32. lim
x
3
2
x
x
2
5
1
33. lim
x
x
3x
2
3
3
34. lim
x
2
3
x
x
2
1
2x
35. lim
x
36. lim
x
x
2
6
x
3
x
2
37. lim
x
1
1
x
x
[Hint: Rationalize the denominator.]
38. lim
x
x
x
2
3
39. lim
x
(
x
2
1
x)
Hint: Multiply by .
In Exercises 40–42, find the limit by adapting the hint for
Exercise 39.
40. lim
x
(x
x
2
4
)
41. lim
x
(
x
2
1
x
2
1
)
42. lim
x
(
x
2
5
x 5
x 1)
THINKERS
In Exercises 43–44, find the limit.
43. lim
x
x
x
44. lim
x
x
x
1
x
2
1
x
x
2
1
x
x
2
2x 1
x
4
2
x
2x
5
x
3
2x 9
5 x
5
3x
4
2x
3
5x
2
x 1
7x
3
4x
2
6x 12
SECTION 13.4 Limits Involving Infinity 923
45. Let x denote the greatest integer function (see Example 7
on page 145) and find:
(a) lim
x
x
x
(b) lim
x
x
x
46. Use the change of base formula for logarithms (Special
Topics 5.4.A) to show that lim
x
l
l
o
n
g
x
x
ln 10.
47. Find lim
x
.
48. Let f(x) be a nonzero polynomial with leading coefficient a,
and let g(x) be a nonzero polynomial with leading coeffi-
cient c. Prove that
(a) If deg f (x) deg g(x), then lim
x
g
f(
(
x
x
)
)
0.
(b) If deg f (x) deg g(x), then lim
x
g
f(
(
x
x
)
)
a
c
.
(c) If deg f (x) deg g(x), then lim
x
g
f(
(
x
x
)
)
does not exist.
Formal definitions of limits at infinity and negative infinity are
given in Exercises 49 and 50. Adapt the discussion in Special
Topics 13.2.A to explain how these definitions are derived from
the informal definitions given in this section.
49. Let f be a function, and let L be a real number. Then the
statement lim
x
f (x) L means that for each positive num-
ber e, there is a positive real number k (depending on e) with
this property:
If x k. then f (x) L e.
[Hint: Concentrate on the second part of the informal
definition. The number k measures “large enough,” that is,
how large the values of x must be to guarantee that f (x) is as
close as you want to L.]
50. Let f be a function, and let L be a real number. Then the
statement lim
x
f (x) L means that for each positive num-
ber e, there is a negative real number n (depending on e)
with this property:
If x n, then f (x) L e.
51. (a) Approximate lim
x
1
1
x
x
to seven decimal places.
(Evaluate the function at larger and larger values of x
until successive approximations agree in the first seven
decimal places.)
(b) Find the decimal expansion of e to at least nine decimal
places.
(c) On the basis of the results in parts (a) and (b), what do
you think is the exact value of lim
x
1
1
x
x
?
(d) Compare this limit to the one in Exercise 46 of Sec-
tion 13.1. How are the two related?
x
x
x
x 1

Chapter 13 Review
IMPORTANT CONCEPTS
Section 13.1
Limit of a function 881
Nonexistence of limits 884–885
Limit of a function from the right 886
Limit of a function from the left 886
Section 13.2
Properties of limits 890
Limits of polynomial and rational
functions 891–893
Limit Theorem 894
Limits of difference quotients 895
Derivative 896
Special Topics 13.2.A
The formal definition of limit 899
Section 13.3
Continuity of a function at x c 906
Continuity from the left and right 907
Continuity on an interval 908
Properties of continuous functions 909
Continuity of composite functions 909
Intermediate Value Theorem 910
Equation Theorem 911
Section 13.4
Infinite limits 914–915
Vertical asymptotes 915
Limit of a function as x approaches
infinity or negative infinity 917
Horizontal asymptotes 917
Properties of limits at infinity 919
924 CHAPTER 13 Limits and Continuity
In Questions 1–4, use a calculator to estimate the limit.
1. lim
x0
3x
x
sin x
2. lim
xp/2
1
1
c
s
o
i
s
n
2
x
x
3. lim
x1
10
x
x
1
.1
4. lim
x0
x 3
x
3
In Questions 5 and 6, use the graph of the function to
determine the limit.
5. lim
x2
f (x)
6. lim
x1
f (x)
In Questions 7–10, assume that lim
x3
f (x) 5 and lim
x3
g(x) 2.
Find the limit.
7. lim
x3
[3f (x) 15] 8. lim
x3
( f (x)[g(x) 2])
y
x
3 2 1
1
1 23
2
3
1
y
x
3 2 1
2
1 23
2
3
1
1
9. lim
x3
f (x)g
[
(
g
x
(
)
x
)]
2
2f (x)
10. lim
x3
f
f
(
(
x
x
)
)
g
2
(
g
x
(
)
x)
In Questions 11–20, find the limit if it exists. If the limit does
not exist, explain why.
11. lim
x2
(x
3
3x 1) 12. lim
x4
2
x
x
2
1
13. lim
x1
x
2
x
2
3
x
1
2
14. lim
x2
x
x
2
2
x
x
6
2
15. lim
x0
1
x
x
1
16. lim
x2
x
x
2
2
6
2
x
x
9
3
17. lim
x1
9 8x
x
2
18. lim
x8
x
x
2
6
8
4
19. lim
x5
x
x
5
5
20. lim
x7
(
7 x
2
6x
2)
21. If f(x) x
2
1, find
lim
h0
f(2 h
h
) f(2)
.
22. If f(x) 3x 2 and c is a constant, find
lim
h0
f(c h
h
) f(c)
.
In Questions 23 and 24, find the rule of the derivative of
the function f.
23. f(x) 4x 2 24. f(x) x
2
In Questions 25 and 26, use the formal definition of limit
to prove the statement.
25. lim
x3
(2x 1) 7 26. lim
x2
1
2
x 3
4
REVIEW QUESTIONS
Chapter
13
Test
Sections 13.1, 13.2; Special Topics 13.2.A
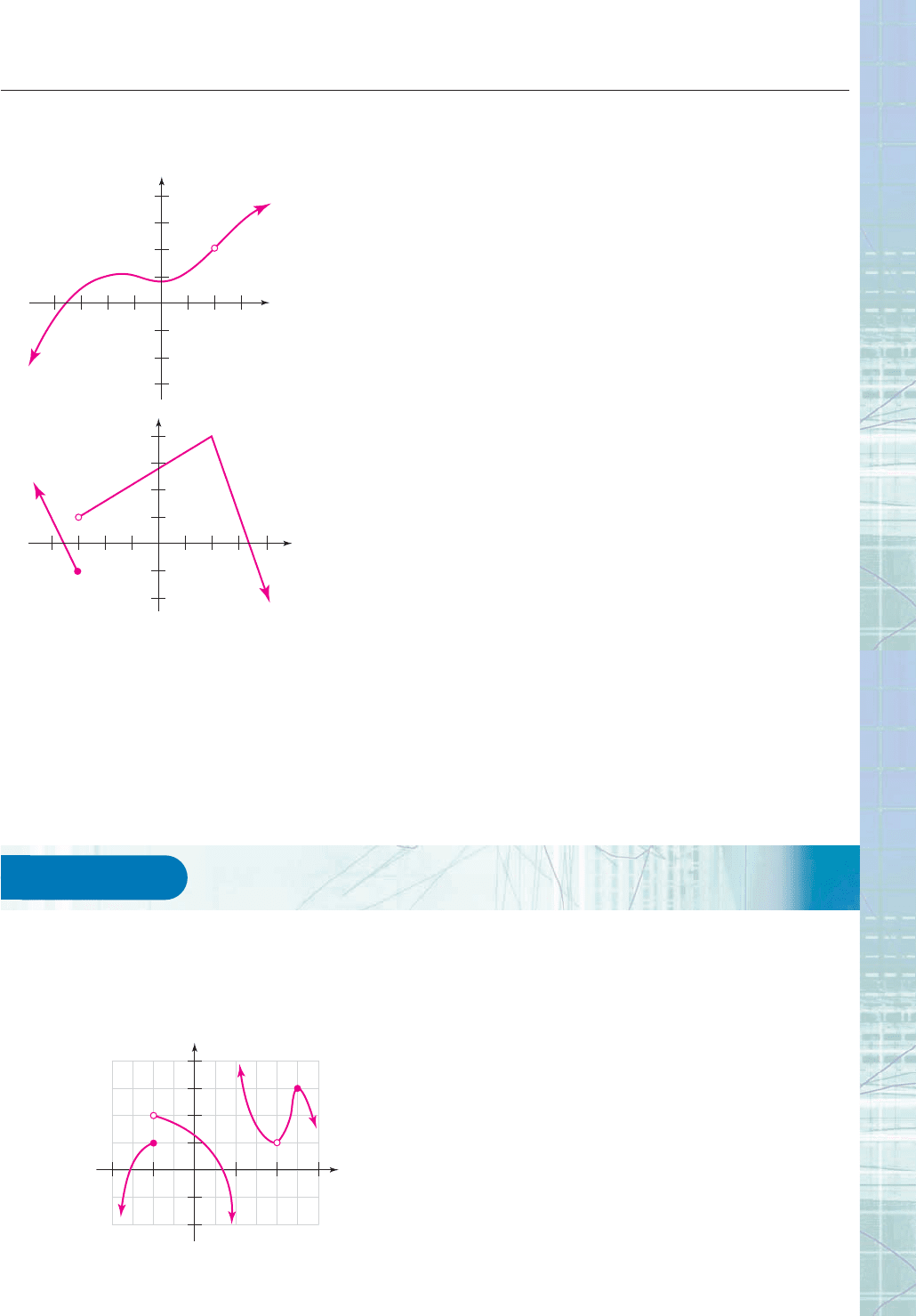
1. Find each of the following limits, where f is the function
whose graph is shown below.
(a) lim
x2
f(x) (b) lim
x2
f(x) (c) lim
x4
f(x) (d) lim
x5
f(x)
6
1
2
2
1
3
4
424 2
x
y
2. Find lim
x2
x
x
2
2
5
3
x
x
1
2
4
. Do not use a calculator or tables.
Show your work.
3. Use numerical or graphical means to find the limit, if it
exists.
lim
x0
e
8x
e
x
e
x
1
2
4. Suppose that f, g and h are functions such that
lim
x4
f(x) 5, lim
x4
g(x) 0, lim
x4
h(x) 8.
Find lim
x4
f(x)
4
h(x
2
)
g(x)
.
CHAPTER 13 Test 925
In Questions 27 and 28, determine whether the function whose
graph is given is continuous at x 3 and x 2.
27.
28.
In Questions 29–32, determine if the function is continuous
at the given points.
29. f(x)
x
2
8
; x 4, x
8
30. g(x) x 3; x 3, x 3
31. h(x)
x
x
7
4
; x 4, x 0
32. f(x)
x
x
2
1
1
; x 1, x 0, x 1
y
x
34 2 1
1
2
1 23 4
2
3
1
y
x
3 2 1
1
2
3
1 23
2
3
1
33. Show that f (x)
x
2
x
2
x
9
6
is
(a) continuous at x 2
(b) discontinuous at x 3.
34. Is the function given by
3x 2ifx 3
f (x)
10 x if x 3
continuous at x 3? Justify your answer.
In Questions 35 and 36, find the vertical asymptotes of the
graph of the given function and state whether the graph moves
upward or downward on each side of each asymptote.
35. f (x)
x
2
x
2
x
1
2
36. g(x)
x
2
x
2
3
x
1
2
In Questions 37–44, find the limit.
37. lim
x3
(x
1
3)
2
38. lim
x2
x
2
x
x
2
2
39. lim
x
si
x
n
2
x
40. lim
x
(ln
x
x)
2
41. lim
x
42. lim
x
4
x
3
3x
2x
2x
5
2
43. lim
x
2
x
x
3
1
4x
3
x
1
44. lim
x
4
3
x
x
2
1
2
In Questions 45 and 46, find the horizontal asymptotes of the
graph of the given function algebraically and verify your
results graphically.
45. f (x)
2
x
x
2
2
x
5x
7
7
46. f(x)
4x
2
x
3
9
x
2
2x
3
3x
2
5x 1
4x
3
2x
2
x 10
