Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

We express this fact by writing
lim
x0
f (x) 1
and saying
the limit of f (x) as x approaches 0 from the left is 1.
The same idea carries over to the general case, in which f is any function and
c and L are real numbers.
886 CHAPTER 13 Limits and Continuity
One-Sided
Limits
Suppose that
as x takes values very close to c (with x c), the corresponding values
of f (x) are very close (and possibly equal) to the real number L
and that
the values of f(x) can be made arbitrarily close to L for all values
of x (with x c) that are sufficiently close to c.
Then we say that
the limit of f (x) as x approaches c from the right is L,
which is written
lim
xc
f (x) L.
The symbol
lim
xc
f (x) L,
which is read
the limit of f (x) as x approaches c from the left is L,
is defined analogously ( just replace “x c” by “x c” in the preceding
definition).
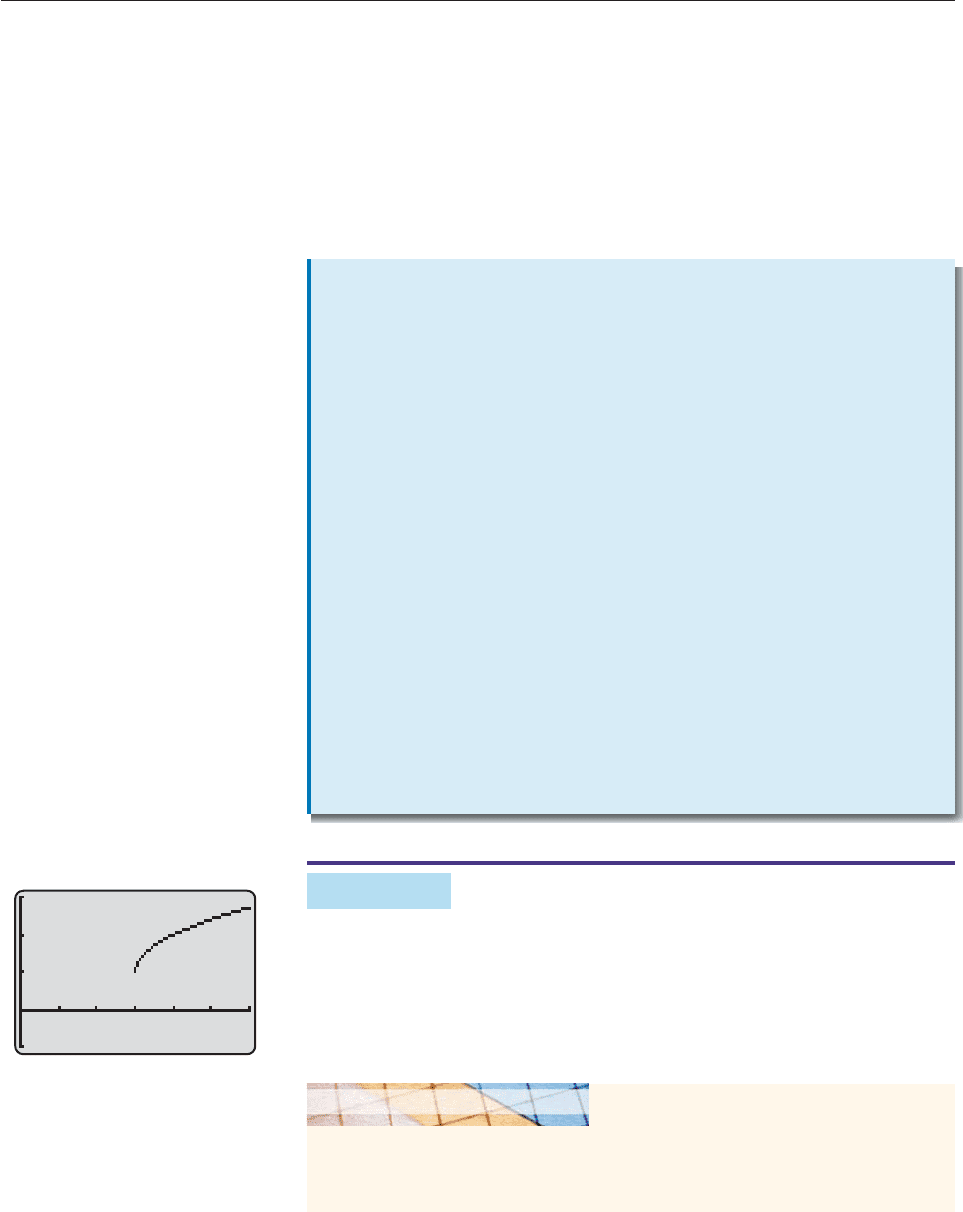
EXAMPLE 9
The function f (x) x 3
1 is defined only when x 3, that is, for values
of x to the right of 3. Find the limit of f (x) as x approaches 3 from the right.
SOLUTION The graph of f in Figure 13–10 suggests that the limit is 1. You can
confirm this by using a very narrow window.
Therefore, we conclude that lim
x3
(x 3
1) 1. ■
Graph f in the viewing window with 2.9999 x 3.0001 and .98 y 1.02. Use
the trace feature to move along the graph. Verify that as x approaches 3 from the
right, the corresponding values of f (x) get closer and closer to 1.
GRAPHING EXPLORATION
3
1
6
0
Figure 13–10

We now have three kinds of limits: the left-hand limits and right-hand limits
defined on the preceding page and the two-sided limits defined on page 881.
Example 9 exhibits a function that has a right-hand limit at x 3 but no left-hand
or two-sided limit. The function in Example 8 has both a left- and a right-hand
limit but no two-sided limit.
When a function has a two-sided limit L at x c, then it automatically has L
as both the left- and right-hand limit at x c. Example 5 illustrates this clearly.
Figures 13–5 and 13–6 show that as x gets closer and closer to 3 (on both sides
of 3), the corresponding values of
f (x)
e
x
x
3
3
1
get closer and closer to 1. So it is certainly true that when x takes values to the
right of 3 (that is, x 3), the corresponding values of f (x) get closer and
closer to 1—and similarly, when x takes values to the left of 3. A similar argu-
ment applies in the general case.
EXAMPLE 10
The graph of the function f in Figure 13–11 shows that f (2) 1 and that
lim
x2
f(x) 3, lim
x2
f (x) 3, lim
x2
f (x) 3.
Figure 13–11
The graph also shows that
lim
x6
f (x) 5 and lim
x6
f (x) 4,
so the two-sided limit, lim
x6
f (x), is not defined. ■
y
x
2468
2
1
4
3
5
SECTION 13.1 Limits of Functions 887
Two-Sided
Limits
Let f be a function and let c and L be real numbers. Then
lim
xc
f(x) L exactly when lim
xc
f (x) L and lim
xc
f (x) L.
CAUTION
Whenever a calculator was used in the
preceding examples, we were careful
to say that the information it provided
suggested that the limit was a
particular number. Although
calculators can provide strong
numerical and graphical evidence for
the existence of a limit, they do not
provide a proof of this fact. In fact,
calculators can occasionally be
misleading (see Exercise 63).
888 CHAPTER 13 Limits and Continuity
EXERCISES 13.1
Note: In the following exercises, “find the limit” means “find
the exact limit, if possible, and otherwise the best possible
approximation.”
In Exercises 1–16, use the table feature of your calculator to
find the limit.
1. lim
x1
x
x
6
4
1
1
2. lim
x2
x
x
5
3
3
8
2
3. lim
x0
tan
x
x
3
x
4. lim
x0
x
tan
si
x
n x
5. lim
x0
x
x
t
s
a
in
n
x
x
6. lim
x0
x
x
s
s
i
i
n
n
2
2
x
x
7. lim
x0
ln
x
x
8. lim
x0
e
2x
x
1
9. lim
x0
e
s
x
in
x
1
10. lim
x0
x sin
1
x
11. lim
xp
1
sin
co
x
s x
12. lim
x
p
2
(sec x tan x)
13. lim
x0
x
(ln x) 14. lim
x0
1
x
x
15. lim
x0
sin
x
(6x)
16. lim
x0
1
sin
s
(
i
3
n
x
(4
)
x)
In Exercises 17–22, use the graph of the function f to determine
the following limits.
lim
x3
f (x) lim
x0
f (x), lim
x2
f (x).
17.
18.
y
x
3 2 1
1
2
3
1 32
2
1
3
y
x
3 2 1
1
1 32
2
1
3
19.
20.
21.
22.
In Exercises 23–26, use the graph of the function f to determine
(a) lim
x2
f(x) (b) lim
x0
f(x)
(c) lim
x3
f(x) (d) lim
x3
f(x)
23.
y
x
3 1
1
2
1 3
2
1
3
y
x
3 2 1
1
2
3
1 32
2
1
3
y
x
3 2 1
1
1 32
2
1
3
y
x
3 2 1
1
2
1 32
2
1
3
y
x
3 2 1
1
2
3
1 2
2
1
3

24.
25.
26.
In Exercises 27–49, use numerical or graphical means to find
the limit, if it exists. If the limit of f as x approaches c does
exist, answer this question: Is it equal to f (c)?
27. lim
x3
5
2
x
x
4
1
28. lim
x2
2
2
x
x
3
5
29. lim
x2
x
x
2
2
5
6
x
x
6
8
30. lim
x2
x
x
2
2
3
x
x
6
2
31. lim
x4
x
x
6
4
32. lim
x3
33. lim
x2
x
2
4
34. lim
x3
9 x
2
35. lim
x4
(x
6
4)
2
36. lim
x2
(x
2x
2)
3
37. lim
x0
e
x
x
1
38. lim
x0
e
2x
e
x
e
x
1
2
39. lim
x1
x
ln
x
1
40. lim
x5
ln x
x
l
5
n5
41. lim
x0
(x ln x) 42. lim
xp/2
x sin x
43. lim
xp/2
x cos x 44. lim
x1
tan px
(x 3)(x 3)(x 4)
(x 4)(x 3)(x 8)
y
x
3 12
1
1 324
2
1
3
y
x
3 1
1
2
1 2
2
1
3
y
x
3 12
1
3
1 324
2
1
3
SECTION 13.1 Limits of Functions 889
45. lim
x1
46. lim
x5
47. lim
x0
cos
p
x
48. lim
x0
tan
p
2
x
49. lim
x1
e
x
sin
p
2
x
50. (a) Approximate lim
x0
(1 x)
1/x
to seven decimal places.
(Evaluate the function at numbers closer and closer to 0
until successive approximations agree in the first seven
decimal places.)
(b) Find the decimal expansion of e to at least nine decimal
places.
(c) On the basis of the results of parts (a) and (b), what do
you think is the exact value of lim
x0
(1 x)
1/x
?
51. (a) Graph the function f whose rule is
3 x if x 2,
x 2if2 x 2,
f(x)
1ifx 2,
4 x if x 2.
Use the graph in part (a) to evaluate these limits:
(b) lim
x2
f (x) (c) lim
x1
f (x) (d) lim
x2
f (x)
52. In Exercise 51, find
(a) lim
x2
f(x) (b) lim
x2
f(x)
(c) lim
x2
f(x) (d) lim
x2
f(x)
53. (a) Graph the function g whose rule is
x
2
if x 1,
x 2if1 x 1,
g(x)
3 x if x 1.
Use the graph in part (a) to evaluate these limits:
(b) lim
x1
g(x) (c) lim
x0
g(x) (d) lim
x1
g(x)
54. In Exercise 53, find
(a) lim
x1
g(x) (b) lim
x1
g(x)
(c) lim
x1
g(x) (d) lim
x1
g(x)
In Exercises 55 and 56, use a unit circle diagram to explain
why the given statement is true.
55. lim
tp/2
sin t 1 56. lim
tp/2
cos t 0
Exercises 57–62 involve the greatest integer function f(x) x,
which was defined in Example 7 on page 145. You may use
your calculator as an aid in analyzing these problems.
57. Let h(x) x x; find lim
x2
h(x), if this limit exists.
58. Let g(x) x x; find lim
x2
g(x), if this limit exists.
59. Find lim
x2
x and lim
x2
x.
60. Find lim
x3
(x x) and lim
x3
(x x).
61. Let r(x)
x
x
x
; find lim
x3
r(x), if this limit exists.
x 5
x 5
x 1
x 1

62. Let k(x)
x
x
x
; find lim
x1
k(x), if this limit exists.
63. If f (x)
1
x
c
1
o
2
s(x
6
)
, then calculus shows that lim
x0
f (x)
1/2. A calculator or computer, however, may indicate
otherwise. Graph f (x) in a viewing window with
.1 x .1,
and use the trace feature to determine the values of f(x) when
x is very close to 0. What does this suggest that the limit is?
890 CHAPTER 13 Limits and Continuity
64. Consider the function t whose rule is
0ifx is rational,
t(x)
1ifx is irrational.
Explain why lim
x4
t(x) does not exist.
13.2 Properties of Limits
■ Learn the algebraic properties of limits.
■ Find limits of polynomial and rational functions.
■ Find the limit of a difference quotient when h approaches 0.
We now consider a number of facts that greatly simplify the computation of
limits.
Although formal proofs of these properties won’t be given here, the central
idea is easily understood.* Consider, for example, Properties 1 and 3. We are
given that
lim
xc
f (x) L and lim
xc
g(x) M.
Consequently, as x gets very close to c, the corresponding values of f (x) are very
close to L, and the corresponding values of g(x) are very close to M. So it seems
plausible that f (x) g(x) is very close to L M and f (x) g(x) is very close to LM.
Section Objectives
Properties
of Limits
If f and g are functions and c, L, M are numbers such that
lim
xc
f (x) L and lim
xc
g(x) M,
then
1. lim
xc
( f (x) g(x)) L M
2. lim
xc
( f (x) g(x)) L M
3. lim
xc
( f (x)
g(x)) L
M
4. lim
xc
g
f (
(
x
x
)
)
M
L
(provided that M 0)
5. lim
xc
f (x)
L
(provided that f (x) 0 for all x near c)
All of these properties remain valid for one-sided limits (that is, when
“xc” is replaced throughout either by “xc
” or by “xc
”).
*A formal proof requires a rigorous definition of “limit.” This rigorous definition and proofs of several
of these properties are discussed in Special Topics 13.2.A.

These properties are often stated somewhat differently. Since lim
xc
f (x) L
and lim
xc
g(x) M, Properties 1–5 can be written as follows.
1. lim
xc
[ f (x) g(x)] lim
xc
f (x) lim
xc
g(x)
2. lim
xc
[ f (x) g(x)] lim
xc
f (x) lim
xc
g(x)
3. lim
xc
[ f (x)
g(x)] lim
xc
f (x)
lim
xc
g(x)
4. lim
xc
g
f (
(
x
x
)
)
l
l
i
i
m
x
m
x
c
c
g
f (
(
x
x
)
)
(provided that lim
xc
g(x) 0)
5. lim
xc
f (x)
lim
xc
f (x
)
(provided that f (x) 0 for all x near c)
LIMITS OF POLYNOMIAL FUNCTIONS
We begin with the most simple polynomial functions, the constant functions, such as
f(x) 5.
To compute lim
xc
f (x), for example, you must ask, “When x is very close to c, what
is the value of f (x)?” The answer is easy, because
no matter what x is, the value of f (x) is always the number 5.
So as x gets closer and closer to c, the value of f (x) is always 5. Hence,
lim
xc
f (x) 5, which is usually written lim
xc
5 5.
The same thing is true for any constant function.
Now consider the identity function, whose rule is f (x) x, and the limit
lim
xc
f (x). When x is very close to c, the corresponding value of f (x) (namely,
x itself) obviously is very close to c. So we have this conclusion.
The preceding facts, together with Limit Properties 1–3, now make it easy to
find the limit of any polynomial function.
EXAMPLE 1
If f (x) x
2
2x 3, find lim
x4
f (x).
SOLUTION By Properties 1 and 2,
lim
x4
f (x) lim
x4
(x
2
2x 3)
lim
x4
x
2
lim
x4
2x lim
x4
3.
Consequently, by Property 3,
lim
x4
f (x) ( lim
x4
x)( lim
x4
x) ( lim
x4
2)( lim
x4
x) lim
x4
3.
SECTION 13.2 Properties of Limits 891
Constant
Limits
If d is a constant, then lim
xc
d d.
Identity Function
Limit
For every real number c, lim
xc
x c.
Using the facts about the limits of constant functions and the identity function in
the preceding boxes, we see that
lim
x4
f (x) ( lim
x4
x)( lim
x4
x) ( lim
x4
2)( lim
x4
x) lim
x4
3
( lim
x4
x)( lim
x4
x) 2( lim
x4
x) 3
(4)(4) 2(4) 3 27.
Note that the limit of f(x) x
2
2x 3 at x 4 is the same as the value of the
function at x 4, namely, f (4) 27. ■
Since any polynomial function consists of sums and products of constants
and x, the argument used in Example 1 works for any polynomial function and
leads to the following conclusion.
This result also applies to one-sided limits because the left- and right-hand limits
at x c must be the same as the two-sided limit (see the box on page 887).
EXAMPLE 2
The function g(x)
9 x
2
is defined only when 3 x 3 (why?). Find
lim
x3
9 x
2
.
SOLUTION By Property 5,
lim
x3
9 x
2
lim
x3
(9
x
2
)
.
The limit under the right-side radical is the limit of the polynomial function
f (x) 9 x
2
. According to the preceding box (and the remark after it), the limit
can be found by evaluating f (x) at 3. Therefore,
lim
x3
9 x
2
lim
x3
(9
x
2
)
9 3
2
0. ■
LIMITS OF RATIONAL FUNCTIONS
Property 4 and the fact that polynomial limits can be found by evaluation make it
easy to compute the limits of rational functions.
EXAMPLE 3
If
f (x)
x
x
3
2
3
6
x
x
2
1
1
0
,
find lim
x2
f (x).
892 CHAPTER 13 Limits and Continuity
Polynomial
Limits
If f (x) is a polynomial function and c is any real number, then
lim
xc
f (x) f (c).
In other words, the limit is the value of the polynomial function at x c.
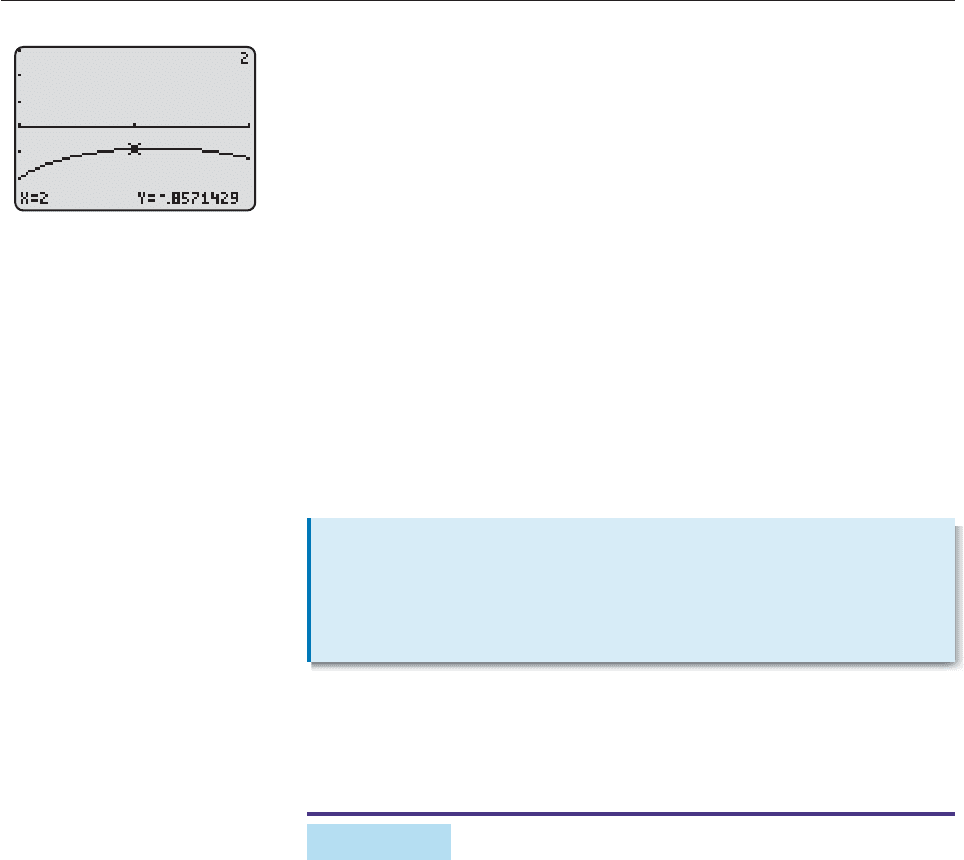
SOLUTION The graph of f (x) near x 2 (Figure 13–12) suggests that the limit
is approximately .86. We can determine the limit exactly by noting that f (x) is
the quotient of two polynomial functions
g(x) x
3
3x
2
10 and h(x) x
2
6x 1,
each of whose limits, as x approaches 2, can be found by evaluation of the func-
tions at x 2. Therefore,
lim
x2
f (x) lim
x2
x
x
3
2
3
6
x
x
2
1
1
0
[Property 4]
6
7
6
7
[Limits of Polynomial Functions]
Note that the limit of f (x), as x approaches 2, is the number f (2). ■
The procedure in Example 3 works for other rational functions as well.
This result is also valid for one-sided limits (see the box on page 887). When a
rational function is not defined at a number, different techniques must be used to
find the limit (if there is one).
EXAMPLE 4
If
f (x)
x
2
x
2x
3
3
,
find lim
x3
f (x).
SOLUTION Since f (x) is not defined when x 3, we cannot find the limit by
evaluation. Nor can we use Property 4 because the limit of the denominator as x
approaches 3 is 0. To find the limit, we first factor the numerator.
x
2
x
2x
3
3
(x
x
1
)(x
3
3)
.
The factor x 3 on the right side may be canceled provided that x 3 0, that
is, provided that x 3. In other words,
x
2
x
2x
3
3
(x
x
1
)(x
3
3)
x 1 for all x 3.
2
3
3
2
2
10
2
2
6
2 1
lim
x2
(x
3
3x
2
10)
lim
x2
(x
2
6x 1)
SECTION 13.2 Properties of Limits 893
3
3
3
1
Figure 13–12
Rational
Limits
Let f (x) be a rational function, and let c be a real number such that f (c) is
defined. Then
lim
xc
f (x) f (c).
In other words, the limit is the value of the function at x c.
The definition of limit, as x approaches 3, involves only the behavior of a function
near x 3 and not at x 3. The preceding equation shows that both f(x) and the
function g(x) x 1 have exactly the same values at all numbers near x 3.
Therefore, they must have the same limit as x approaches 3. Therefore,
lim
x3
x
2
x
2x
3
3
lim
x3
(x 1) 3 1 4. ■
The technique in Example 4 applies in many cases. When two functions have
identical behavior, except possibly as x c, they will have the same limit as x
approaches c. More precisely,
EXAMPLE 5
Find lim
x4
x
x
4
2
.
SOLUTION Property 4 does not apply here since the limit of the denominator
is 0 when x approaches 4. However, the denominator can be factored.
x 4 (x
2)(x
2).
Consequently,
x
x
4
2
x
1
2
x
x
2
2
.
When x 4, then x
2 0 and
x
x
2
2
1, so
x
x
4
2
x
1
2
x
x
2
2
x
1
2
for all x 4.
By the Limit Theorem,
lim
x4
x
x
4
2
lim
x4
x
1
2
[Property 4]
[Property 1]
[Property 5]
1
4
. [Constant Limits; Polynomial Limit] ■
1
4
2
lim
x4
1
lim
x4
x
lim
x4
2
lim
x4
1
lim
x4
x
lim
x4
2
lim
x4
1
lim
x4
(x
2)
x
2
(x
2)(x
2)
894 CHAPTER 13 Limits and Continuity
Limit
Theorem
If f and g are functions that have limits as x approaches c and
f (x) g(x) for all x c,
then
lim
xc
f (x) lim
xc
g(x).

LIMITS OF DIFFERENCE QUOTIENTS
Limits involving the difference quotient of a function play an important role in
calculus. Recall from Section 3.2 that the difference quotient of a function f is the
quantity
f (x h
h
) f (x)
.
In limit computations with difference quotients, the variable is the quantity h and
x is treated as a constant.
EXAMPLE 6
Suppose f (x) x
2
.
(a) Find and simplify the difference quotient of f, when x 5.
(b) Find the limit of this difference quotient as h approaches 0.
SOLUTION
(a)
f(5 h
h
) f(5)
(5 h
h
)
2
5
2
10h
h
h
2
.
(b) lim
h0
f(5 h
h
) f(5)
lim
h0
10h
h
h
2
lim
h0
h(10
h
h)
[Factor numerator]
lim
h0
(10 h) [Limit Theorem]
10 0 10. [Limit of a polynomial function] ■
EXAMPLE 7
Find the limit of the difference quotient of f(x) x
as h approaches 7.
SOLUTION The difference quotient is
f (x h
h
) f (x)
x h
h
x
.
Rationalizing the numerator of the last fraction (as was done in Example 9 of
Section 5.1) shows that the fraction on the right above is equal to
.
1
x h
x
(25 10h h
2
) 25
h
SECTION 13.2 Properties of Limits 895
