Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


The preceding analysis leads to the following.
Strictly speaking, it isn’t necessary to list all three of the conditions in the defini-
tion, since condition (iii) implies that the other two conditions hold.
EXAMPLE 1
Without graphing, show that the function
f (x)
x
2
x
x
5
1
is continuous at x 3.
SOLUTION
f (3)
8
13
,
and by the properties of limits (page 890),
lim
x3
f (x) lim
x3
x
2
x
x
5
1
8
13
.
Therefore, lim
x3
f (x) f (3), and hence, f is continuous at x 3. ■
The properties of limits (Section 13.2) and the definition of continuity pro-
vide justification for assumptions made about various graphs in earlier chapters.
For example, in Section 13.2, we saw that for any polynomial or rational function
f and any number c such that f (c) is defined,
lim
xc
f (x) f (c).
Thus, every polynomial and every rational function is continuous wherever it is
defined. That proves the first two of the following statements.
(3)
2
(3
) 1
(3) 5
lim
x3
(x
2
x
1)
lim
x3
(x 5)
lim
x3
x
2
x
1
lim
x3
(x 5)
(3)
2
(3
) 1
(3) 5
906 CHAPTER 13 Limits and Continuity
Definition
of Continuity
Let f be a function that is defined for all x in some open interval containing
c. Then f is said to be continuous at x c provided that
(i) f (c) is defined;
(ii) lim
xc
f (x) exists; and
(iii) lim
xc
f (x) f (c).
The facts in the preceding box justify the graphing techniques used in this
book. Plotting points (a few when graphing by hand, many when graphing with
technology) and connecting them with an unbroken curve is a reasonable proce-
dure when graphing continuous functions.
CONTINUITY ON AN INTERVAL
Now let us consider continuity at an endpoint of the graph of a function f, such as
(a, f (a)) or (b, f (b)) in Figure 13–17.
Figure 13–17
The intuitive idea of continuity at (a, f (a)) is that we can draw the graph of f at,
and to the right of, the point (a, f (a)) without lifting the pencil from the paper.
Essentially the same analysis that was given above can be made here, provided
that we consider only values of x to the right of x a. It shows that the intuitive
idea of continuity at x a is equivalent to a statement about right-hand limits,
namely, lim
xa
f (x) f (a). An analogous discussion (with left-hand limits) applies
to the endpoint (b, f (b)) and leads to this definition.
(a, f(a)) (b, f(b))
SECTION 13.3 Continuity 907
Continuous
Functions
Each of the following functions is continuous at every number in its domain.
1. Polynomial functions
2. Rational functions
3. The exponential functions
f (x) 10
x
, g(x) e
x
, h(x) b
x
4. The logarithmic functions
f (x) log x, g(x) ln x, h(x) log
b
x
5. The trigonometric functions
f (x) sin x, g(x) cos x, h(x) tan x,
k(x) csc x, r(x) sec x, s(x) cot x
6. The inverse trigonometric functions
f (x) sin
1
x, g(x) cos
1
x, h(x) tan
1
x
Continuity from
the Left and Right
A function f is continuous from the right at x a provided that
lim
xa
f (x) f (a).
A function f is continuous from the left at x b provided that
lim
xb
f (x) f (b).
EXAMPLE 2
The function f (x) x
, which is not defined when x 0, is continuous from the
right at x 0 because f (0) 0
0 and
lim
x0
f (x) lim
x0
x
0 f (0). ■
The most useful functions are those that are continuous at every point in an
interval. Intuitively, this means that their graphs can be drawn over the entire in-
terval without lifting the pencil from the paper. As we saw above, most of the
functions in this book are of this type. Here is a formal definition.
Analogous definitions may be given for continuity on intervals of the form [a, b),
(a, b], (a, ), [a, ), (, b), and (, b].
EXAMPLE 3
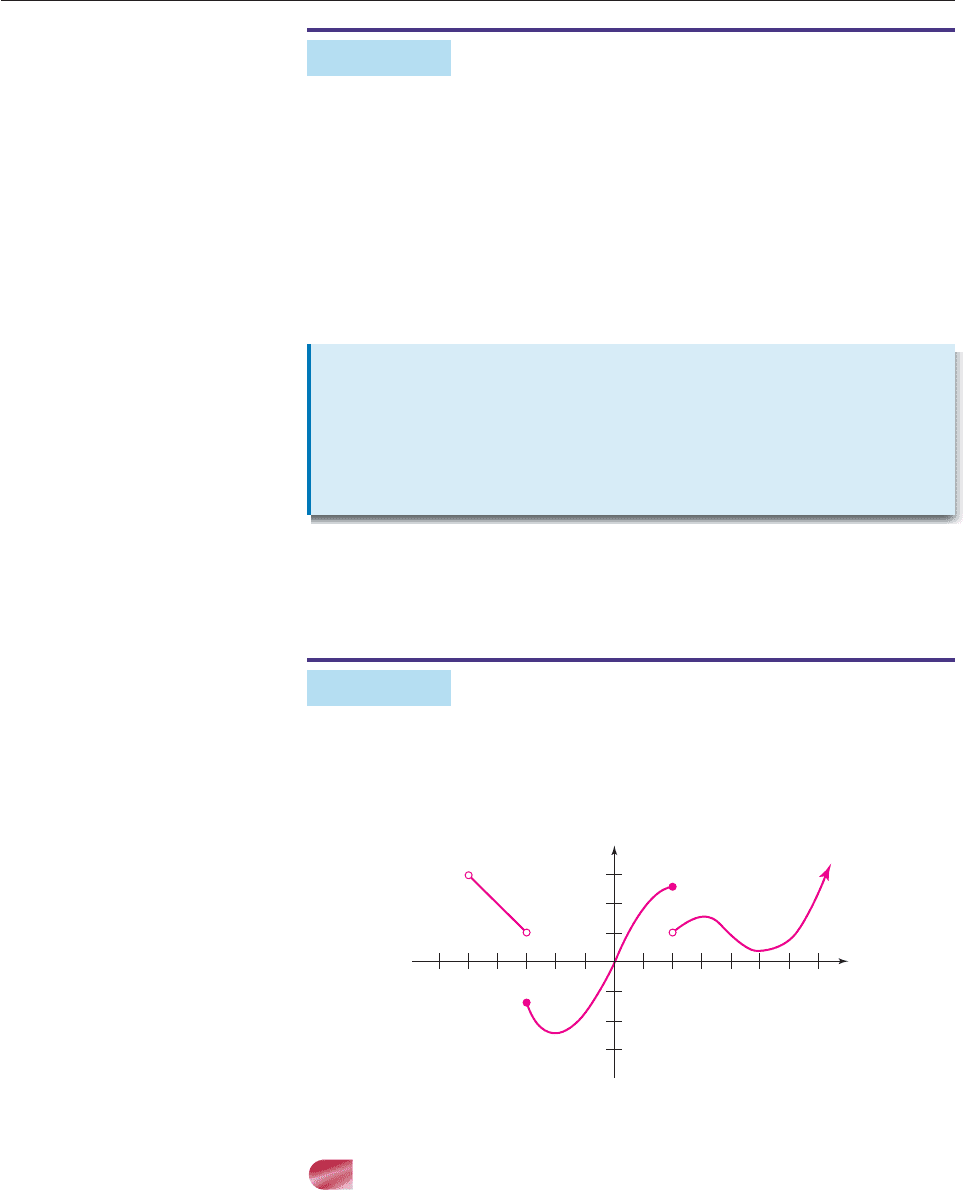
The function f whose graph is shown in Figure 13–18 is discontinuous at x 3
and x 2 but is continuous on each of the intervals (5, 3), [3, 2],
and (2, ). ■
Figure 13–18
PROPERTIES OF CONTINUOUS FUNCTIONS
Using the definition is not always the most convenient way to show that a partic-
ular function is continuous. It is often easier to establish continuity by using the
following facts.
y
x
35
1
2
2
2
1
908 CHAPTER 13 Limits and Continuity
Continuity on
an Interval
A function f is said to be continuous on an open interval (a, b) provided
that f is continuous at every number in the interval.
A function f is said to be continuous on a closed interval [a, b] provided
that f is continuous from the right at x a, continuous from the left at
x b, and continuous at every number in the open interval (a, b).

Proof 1. By the definition of the sum function, ( f g)(x) f (x) g(x).
Since f and g are continuous at x c, we know that
lim
xc
f (x) f (c) and lim
xc
g(x) g(c).
Therefore, by the first property of limits (see page 890),
lim
xc
( f g)(x) lim
xc
( f (x) g(x)) lim
xc
f (x) lim
xc
g(x)
f (c) g(c)
( f g)(c).
This says that f g is continuous at x c.
The remaining statements are proved similarly, using limit properties 2, 3,
and 4. ■
EXAMPLE 4
We noted above that the function f (x) sin x is continuous at x 0. We also
know that the polynomial function g(x) x
3
5x 2 is continuous at x 0.
Therefore, each of the following functions is continuous at x 0.
( f g)(x) sin x x
3
5x 2
( f g)(x) sin x (x
3
5x 2) sin x x
3
5x 2
( fg)(x) (sin x)(x
3
5x 2)
g
f
(x)
x
3
sin
5x
x
2
(Note that g(0) 0.) ■
Composition of functions is often used to construct new functions from
given ones.
EXAMPLE 5
The polynomial function f (x) x
3
3x
2
x 7 is continuous at x 2, and
f (2) 2
3
3
2
2
2 7 5. The function g(x) x
is continuous at x 5
because by Limit Property 5 (page 890).
lim
x5
x
lim
x5
x
5
g(5).
SECTION 13.3 Continuity 909
Properties of
Continuous Functions
If the functions f and g are continuous at x c, then each of the following
functions is also continuous at x c.
1. The sum function f g
2. The difference function f g
3. The product function fg
4. The quotient function f/g (provided that g(c) 0)
Continuity of
Composite Functions
If the function f is continuous at x c and the function g is continuous at
x f (c), then the composite function g f is continuous at x c.
By the box above (with c 2 and f (c) f (2) 5), the composite function g f,
which is given by
(g f )(x) g( f (x)) g(x
3
3x
2
x 7)
x
3
3
x
2
x
7
,
is also continuous at x 2. ■
THE INTERMEDIATE VALUE THEOREM
The following property of continuous functions has several important appli-
cations.
Although we shall not prove the Intermediate Value Theorem, we can demon-
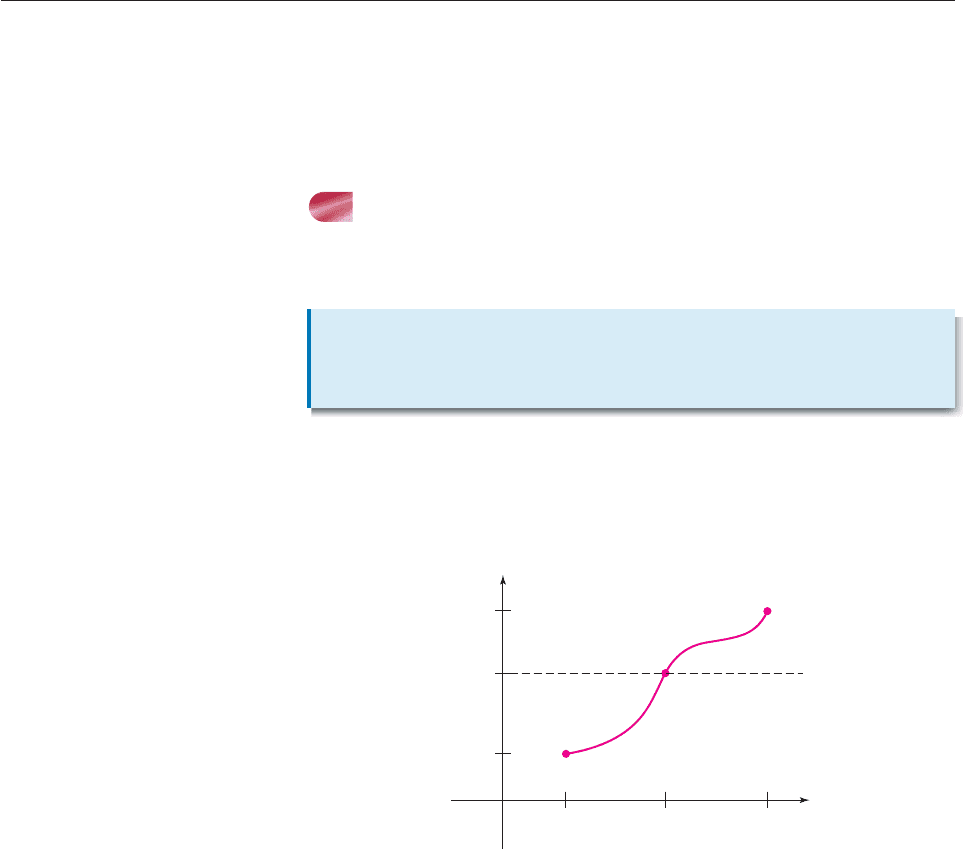
strate its plausibility by a simple geometric argument. Figure 13–19 shows the
graph of a function f that is continuous on the interval [a, b] and a number k that
is between f (a) and f (b).
Figure 13–19
Because f is continuous on the interval, its graph can be drawn from (a, f (a)) to
(b, f (b)) without lifting the pencil from the paper. As Figure 13–19 suggests, there
is no way to do this unless the graph crosses the horizontal line y k at least once
between x a and x b. The coordinates of a point where the graph crosses the
line can be described in two ways:
(c, f (c)) because the point is on the graph of f ;
(c, k) because the point is on the line y k.
Thus, this point satisfies the conclusion of the Intermediate Value Theorem:
a c b and f (c) k.
The Intermediate Value Theorem further explains why the graph of a contin-
uous function is connected and unbroken. If f is continuous on the interval
[a, b], then its graph cannot go from the point (a, f (a)) to the point (b, f (b)) with-
out moving through all the y values between f (a) and f (b).
y
x
acb
k
(b, f(b))
(a, f(a))
(c, f(c)) (c, k)
f(a)
f(b)
910 CHAPTER 13 Limits and Continuity
Intermediate
Value Theorem
If the function f is continuous on the closed interval [a, b] and k is any num-
ber between f (a) and f (b), then there exists at least one number c between
a and b such that f (c) k.
Here is an important special case of the Intermediate Value Theorem.
Proof Since one of f (a) and f (b) is positive and the other is negative, the
number 0 is between them. By the Intermediate Value Theorem, there is a number
c between a and b such that f (c) 0. ■
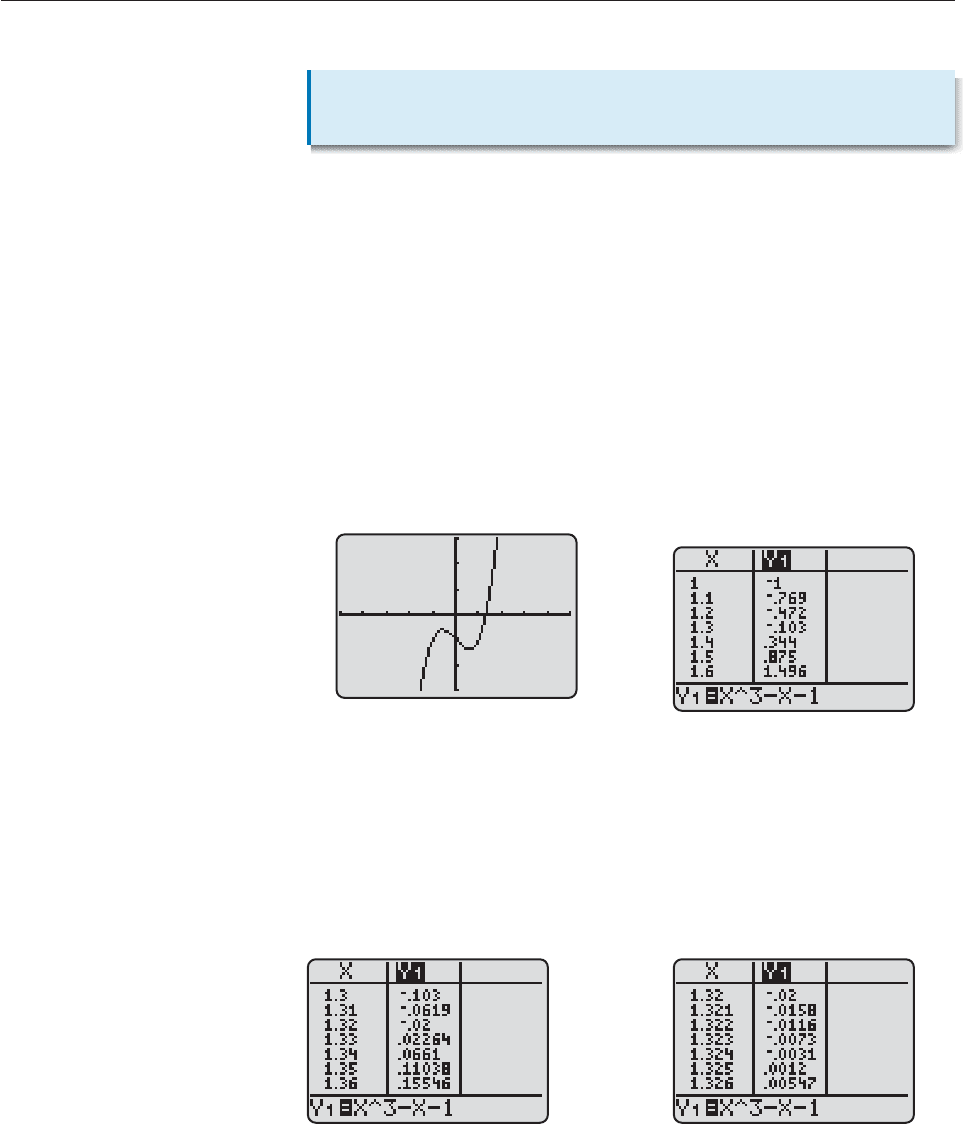
Many root finders on calculators are based on the Equation Theorem. To see
why, consider the equation
x
3
x 1 0.
The graph of f (x) x
3
x 1 in Figure 13–20 shows that there is a solution
between 1 and 2. So we evaluate f (x), beginning at x 1 and moving by tenths,
as in Figure 13–21. Since f (1.3) and f (1.4) have opposite signs, the solution is
between 1.3 and 1.4 by the Equation Theorem. Hence, the decimal expansion of
the solution begins with 1.3.
Figure 13–20 Figure 13–21
Now evaluate f (x) beginning at 1.3 and moving by hundredths, as in Fig-
ure 13–22. Since f (1.32) and f (1.33) have opposite signs, the solution is between
1.32 and 1.33. So its decimal expansion begins with 1.32. Next evaluate f (x)
beginning at 1.32 and moving by thousandths, as in Figure 13–23, which shows
that the solution is between 1.324 and 1.325. Thus, its decimal approximation
begins 1.324. Each time the evaluation procedure is carried out, one more decimal
place in the solution is found.
Figure 13–22 Figure 13–23
Root finders use this process (or a variation of it) to approximate solutions to
as many decimal places as the calculator can handle. The Equation Theorem is
also the reason that a root finder that cannot find a solution may display an error
message that reads “no sign change.”
3
3
5
5
SECTION 13.3 Continuity 911
Equation
Theorem
If the function f is continuous on the interval [a, b] and f (a) and f (b) have
opposite signs, then the equation f (x) 0 has a solution between a and b.
912 CHAPTER 13 Limits and Continuity
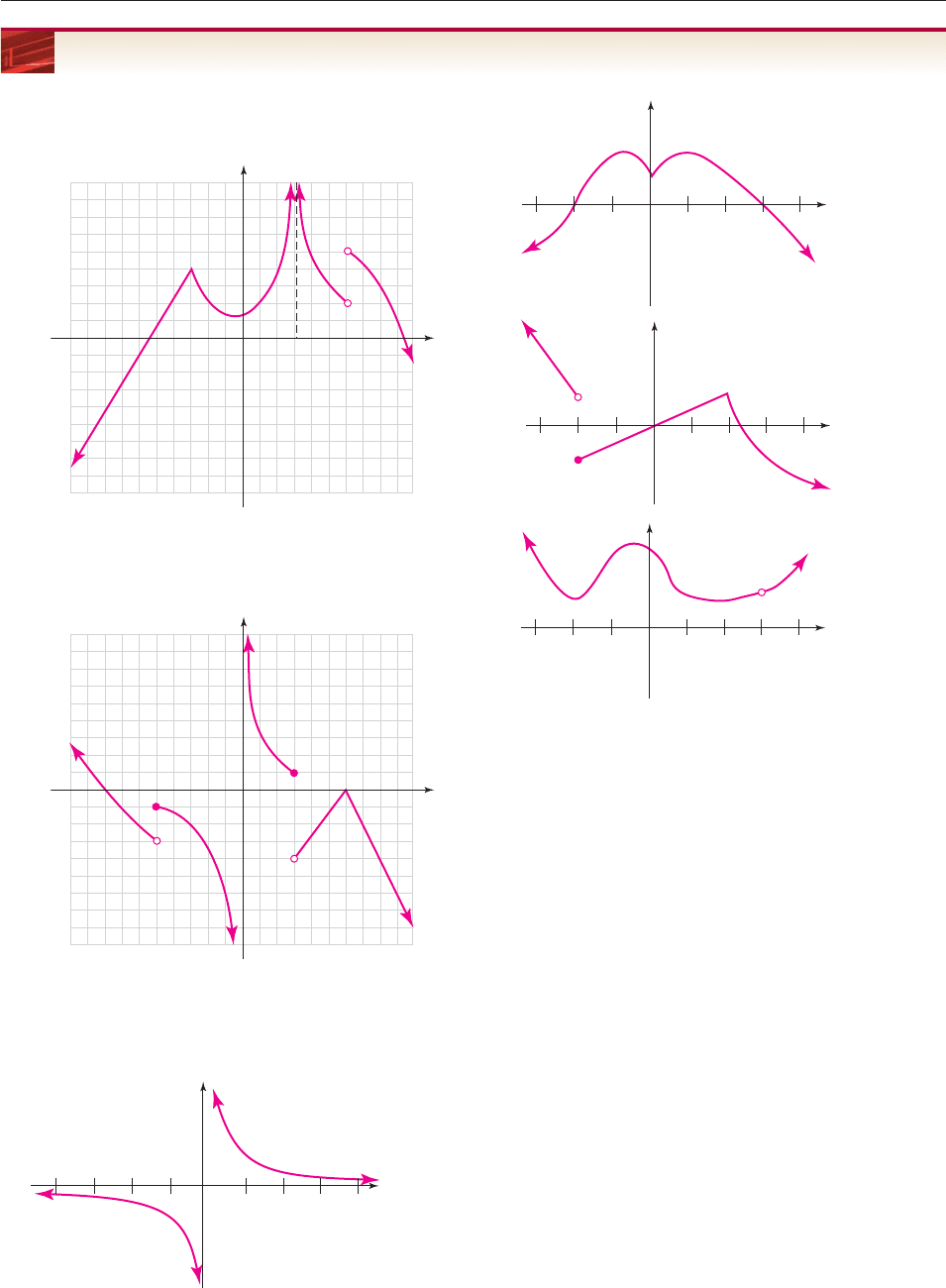
EXERCISES 13.3
1. Use the graph of the function f in the figure to find all the
numbers at which f is not continuous.
2. Use the graph of the function g in the figure to find all the
numbers at which g(x) is defined but not continuous.
In Exercises 3–6, determine whether the function whose graph
is given is continuous at x 2, at x 0, and at x 3.
3.
1 31
y
x
1
1
y
x
y
x
1 3
4.
5.
6.
In Exercises 7–12, use the definition of continuity and the
properties of limits to show that the function is continuous at
the given number.
7. f (x) x
2
5(x 2)
7
at x 3
8. g(x) (x
2
3x 10)(x
3
2x
2
5x 4) at x 1
9. f (x) at x 2
10. h(x) at x 2
11. f (x)
(x
x
6
x
)
2
at x 36
12. k(x)
2x
8
2
x
5
2
at x 2
In Exercises 13–18, explain why the function is not continuous
at the given number.
13. f(x) 1/(x 3)
3
at x 3
14. h(x)
x
2
x
2
x
4
2
at x 2
15. f (x)
x
x
2
2
4
x
x
2
3
at x 1
sin(p/x)ifx 0
16. g(x)
at x 0
1ifx 0
x 3
(x
2
x 1)(x
2
1)
x
2
9
(x
2
x 6)(x
2
6x 9)
x
113
y
y
x
113
y
x
113

x
2
if x 0
17. f (x)
at x 0
1ifx 0
18. f (x)
2 x
x
2
at x 0
In Exercises 19–24, determine whether or not the function is
continuous at the given number.
2x 4ifx 2
19. f(x)
at x 2
2x 4ifx 2
2x 5ifx 1
20. g(x)
at x 1
2x 1ifx 1
x
2
x if x 0
21. f (x)
at x 0
2x
2
if x 0
x
3
x 1ifx 2
22. g(x)
at x 2
3x
2
2x 1ifx 2
23. f (x) x 3 at x 3
24. k(x) x 2 3atx 2
In Exercises 25–28, determine all numbers at which the
function is continuous.
x
x
2
2
4
x
x
2
3
if x 1
25.
f (x)
3/2ifx 1
x
2
x
2
x
4
6
if x 2
26.
g(x)
5/4ifx 2
x
2
1ifx 0
27. f(x)
x if 0 x 2
2x 3ifx 2
1/x if x 1 and x 0
28. h(x)
x
2
if x 1
In Exercises 29–32, justify your answers.
29. Taxis in New York City cost $2 plus 30 cents for each 1/5
of a mile (or portion thereof). Let f (x) be the cost of travel-
ing x miles. Is f continuous on the interval [0, 3]?
30. On a four and a half hour flight from Chicago to Seattle, let
h(x) be the height of the plane above the ground at time
x hours. Is h continuous on the interval [0, 4.5]?
31. The U.S. Weather Bureau at Hopkins Airport in Cleveland
continuously records the temperature. If g(x) is the tempera-
ture at time x hours, where x 0 corresponds to midnight, at
what points on the interval [0, 24] is g continuous?
32. Postage on a letter from the United States to Germany is
80 cents for each ounce (or fraction thereof) for letters
weighing up to 8 ounces. Let f (x) be the postage for a letter
weighing x ounces. At what points on the interval (0, 8] is f
continuous?
33. If you don’t have a calculator and you don’t remember
how to find square roots by hand, explain how you could
use the Equation Theorem (and a lot of pencil and paper
SECTION 13.3 Continuity 913
multiplication and addition) to find the decimal expansion of
7
. [Hint: What are the solutions of x
2
7 0?]
34. (a) The function whose graph is shown in Figure 13–2 on
page 882 is discontinuous at an infinite number of
places. Where is it discontinuous?
(b) Explain why a rational function cannot be discontinu-
ous at an infinite number of places.
THINKERS
35. Show that the function
f (x)
x
4
x
5
x
2
1
4
is not continuous on [3, 3] but does satisfy the conclusion
of the Intermediate Value Theorem (that is, if k is a number
between f (3) and f (3), there is a number c between 3
and 3 such that f (c) k). [Hint: What can be said about f on
the intervals [3, 2] and [2, 3]?]
36. Show that the function
f (x)
x
4
x
2
2
x
3
is not continuous on [3, 3] and does not satisfy the con-
clusion of the Intermediate Value Theorem (that is, there is
a number k between f (3) and f (3) for which there is no
number c between 3 and 3 such that f (c) k).
37. For what values of b is the function
bx 4ifx 3
f (x)
bx
2
2ifx 3
continuous at x 3?
38. Show that f (x)
x
is continuous at x 0.
A function f that is not defined at x c is said to have a
removable discontinuity at x c if there is a function g such
that g(c) is defined, g is continuous at x c, and g(x) f (x)
for x c. In Exercises 39–43, show that the function f has a
removable discontinuity by finding an appropriate function g.
39. f (x)
x
x
2
1
1
40. f (x)
x
x
2
41. f (x)
2
4
x
x
42. f (x)
sin
x
x
[Hint: See Example 4 on pages 882–883.]
43. Show that the function f (x)
x
x
has a discontinuity at
x 0 that is not removable.
44. A ranger leaves his truck at a parking lot at the trail head at
8:00
A.M. and hikes 11 miles to a fire tower, arriving there at
noon. He stays overnight and starts back along the same trail
at 8:00
A.M., arriving at the parking lot at noon. Show that
there is a point on the trail that he passes at exactly the same
time on both days. [Hint: Let f (t) be his distance from the
parking lot at time t on the first day, and let g(t) be his dis-
tance from the parking lot at time t on the second day. Use an
appropriate theorem to solve the equation f (t) g(t).]
914 CHAPTER 13 Limits and Continuity
13.4 Limits Involving Infinity
■ Understand the definitions and properties of limits at infinity.
■ Use limits at infinity to find the horizontal asymptotes of a graph.
■ Find limits of rational functions.
In the following discussion, it is important to remember that
There is no real number called “infinity,” and the symbol ,
which is usually read “infinity,” does not represent any real number.
Nevertheless, the word “infinity” and the symbol are often used as a convenient
shorthand to describe the way some functions behave under certain circumstances.
General speaking, “infinity” indicates a situation in which some numerical quan-
tity gets larger and larger without bound, meaning that it can be made larger than
any given number. Similarly, “negative infinity” (in symbols ) indicates a sit-
uation in which a numerical quantity gets smaller and smaller without bound,
meaning that it can be made smaller than any given negative number.
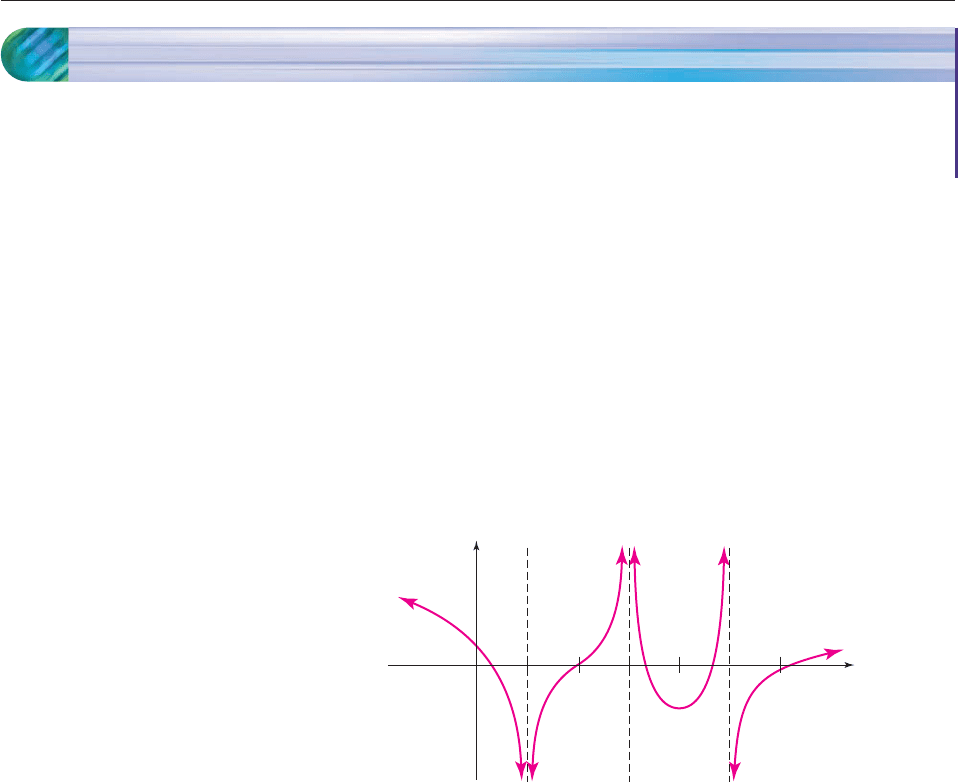
Consider the function f whose graph is shown in Figure 13–24.
Figure 13–24
The graph shows that as x approaches 3 from the left or right, the corresponding
values of f (x) do not get closer and closer to a particular number. Instead, they
become larger and larger without bound. Although there is no limit in the sense
defined in Section 13.1, it is convenient to describe this situation symbolically by
writing
lim
x3
f(x)
which is read “the limit of f(x) as x approaches 3 is infinity.” Similarly, f does not
have a limit as x approaches 1 (from the left or right) because the corresponding
values of f (x) get smaller and smaller without bound. We say that “the limit of f (x)
as x approaches 1 is negative infinity” and write
lim
x1
f (x) .
Near x 5, the values of f (x) get very large on the left side of 5 and very small on
the right side of 5, so we write
lim
x5
f (x) and lim
x5
f (x)
y
x
31 5
Section Objectives
and say “the limit as x approaches 5 from the left is infinity” and “the limit as x
approaches 5 from the right is negative infinity.”
There are many cases like the ones illustrated above in which the language of
limits and the word “infinity” is useful for describing the behavior of a function
that actually does not have a limit in the sense of Section 13.1.
EXAMPLE 1
How does f (x) 5/x
4
behave near x 0?
SOLUTION
EXAMPLE 2
Describe the behavior of the function
g(x)
x
2
2
8
x 8
near x 2.
SOLUTION
The “infinite limits” considered in Figure 13–24 and Examples 1 and 2 can
be interpreted geometrically. Each such limit corresponds to a vertical asymptote
of the graph. Consequently, we have this formal definition.
SECTION 13.4 Limits Involving Infinity 915
Graph f (x) in the viewing window with .5 x .5 and 500,000 y 0. Use
the trace feature to move along the graph on both sides of x 0 and confirm that
lim
x0
x
4
5
.
■
GRAPHING EXPLORATION
Graph g(x) in a suitable viewing window around x 2, and verify that
lim
x2
x
2
2
8
x 8
and lim
x2
x
2
2
8
x 8
.
■
GRAPHING EXPLORATION
Vertical
Asymptotes
The vertical line x c is a vertical asymptote of the graph of the function
f if at least one of the following is true:
lim
xc
f (x) , lim
xc
f (x) ,lim
xc
f (x) ,
lim
xc
f (x) , lim
xc
f (x) , lim
xc
f (x) .
