Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

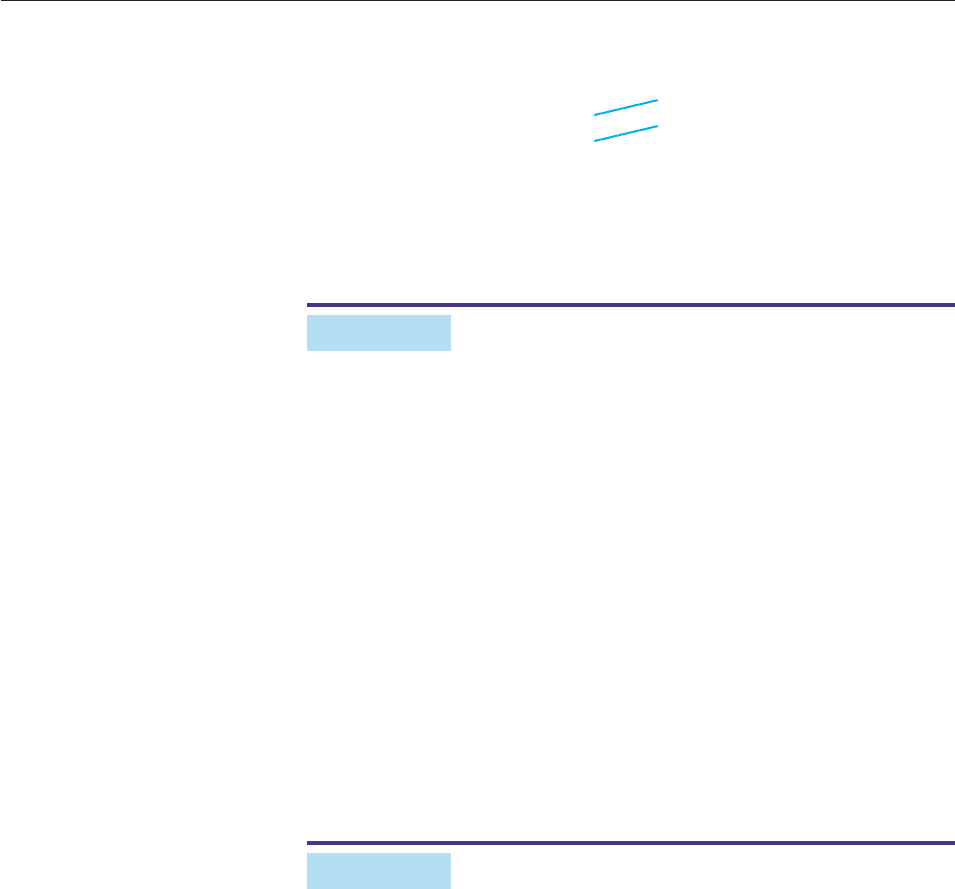
SOLUTION Proceed as we did in Example 1: Factor numerator and denomi-
nator, and cancel common factors.
x
x
2
2
3
x
x
6
2
(
(
x
x
2
2
)
)
(
(
x
x
3
1
)
)
x
x
3
1
■
To add or subtract two fractions with the same denominator, simply add or
subtract the numerators.
a
b
b
c
a
b
c
and
a
b
b
c
a
b
c
EXAMPLE 4
7
x
x
2
2
3
2
4x
2
x
2
2x
3
5
3x
2
x
2
2x
3
7
. ■
To add or subtract fractions with different denominators, you must use a
common denominator, that is, replace the given fractions by equivalent ones that
have the same denominator. For instance, to add 1/3 and 1/4, we use the com-
mon denominator 12 (the product of 3 and 4):
1
3
1
4
2
and
1
4
1
3
2
,
so that
1
3
1
4
1
4
2
1
3
2
4
1
2
3
1
7
2
.
EXAMPLE 5
Compute:
2x
3
x
1
x
x
2
1
2
.
SOLUTION We use the product of the denominators 3x(x 1) as the common
denominator. To rewrite the first fraction in terms of this denominator, we must
find the right-side numerator here.
2x
3
x
1
3x(x
?
1)
Note that to get from the left-side denominator to the right-side one, you multiply
by x 1. To keep the fractions equal, you must multiply the left-hand numerator
by x 1 also:
2x
3
x
1
(2x
3
x(x
1)
(x
1
)
1)
7x
2
2 4x
2
2x 5
x
2
3
(7x
2
2) (4x
2
2x 5)
x
2
3
946 APPENDIX 1 Algebra Review

SECTION 1.D Fractional Expressions 947
A similar procedure works with the other fraction.
x
x
2
1
2
3x(x
?
1)
x
x
2
1
2
3
3
x
x
(
(
x
x
2
1
2
)
)
Multiply by 3x
Now that the fractions have the same denominator, it’s easy to subtract them.
2x
3
x
1
x
x
2
1
2
(2x
3
x(x
1)
(x
1
)
1)
3
3
x
x
(
(
x
x
2
1
2
)
)
■
Although the product of the denominators can always be used as a common
denominator, it’s usually more efficient to use the least common denominator,
that is, the smallest quantity that can be the denominator of both fractions. The
next example illustrates an easy way to find the least common denominator when
dealing with numbers.
EXAMPLE 6
Find the least common denominator for
1
1
00
and
1
1
20
.
SOLUTION The two denominators can be factored as
100 2
2
5
2
and 120 2
3
3
5.
The distinct factors that appear in both numbers are 2, 3, and 5. For each factor,
take the highest power to which it appears in either number (namely, 2
3
, 3
1
, and
5
2
). The product of these highest powers is the least common denominator.
2
3
3
5
2
600
Note that 600 100
6 and 600 120
5, so
1
1
00
1
1
00
6
6
6
6
00
and
1
1
20
1
1
20
5
5
6
5
00
. ■
The technique of Example 6 can also be used to find the least common
denominator of rational expressions.
EXAMPLE 7
Find the least common denominator for
x
2
2
1
x 1
,
x
2
5
x
x
, and
x
3
4
x
x
7
3
and express each fraction in terms of this common denominator.
3x
3
2x
2
5x 1
3x
2
3x
2x
2
x 1 3x
3
6x
3x
2
3x
(2x 1)(x 1) 3x(x
2
2)
3x(x 1)

SOLUTION Begin by factoring each denominator completely.
x
2
2x 1 (x 1)
2
x
2
x x(x 1) x
4
x
3
x
3
(x 1)
The distinct factors are x, x 1, and x 1. The least common denominator is
x
3
(x 1)
2
(x 1).
Therefore,
(x
1
1)
2
(x
1
1)
2
x
x
3
3
(
(
x
x
1
1
)
)
x
3
(x
x
3
(x
1)
2
(x
1)
1)
x(x
5
x
1)
x(x
5
x
1)
x
x
2
2
(
(
x
x
1
1
)
)
2
2
x
3
(x
5x
3
(x
1)
2
(x
1)
2
1)
x
3
3
(
x
x
7
1)
x
3
3
(
x
x
7
1)
(
(
x
x
1
1
)
)
(
(
x
x
1
1
)
)
. ■
EXAMPLE 8
Compute
1
z
z
3z
1
(z
z
2
1)
2
.
SOLUTION We use the least common denominator z(z 1)
2
and express each
fraction in terms of this denominator.
1
z
1
z
(
(
z
z
1
1
)
)
2
2
z
(
(
z
z
1
1
)
)
2
2
z
3z
1
z
3z
1
z
z
(
(
z
z
1
1
)
)
3
z
z
(
2
z
(z
1)
1
2
)
(z
z
2
1)
2
(z
z
2
1)
2
z
z
z(z
z
3
1)
2
Then
1
z
z
3z
1
(z
z
2
1)
2
z
(
(
z
z
1
1
)
)
2
2
3
z
z
(
2
z
(z
1)
1
2
)
z(z
z
3
1)
2
. ■
Multiplication of fractional expressions is done in the same way as multipli-
cation of numerical fractions.
2z
3
4z
2
2z 1
z(z 1)
2
z
2
2z 1 3z
3
3z
2
z
3
z(z 1)
2
(z 1)
2
3z
2
(z 1) z
3
z(z 1)
2
(3x 7)(x 1)(x 1)
x
3
(x 1)
2
(x 1)
948 APPENDIX 1 Algebra Review
Multiplication of Fractional
Expressions
If a, b, c, and d are algebraic expressions, then
a
b
d
c
b
a
d
c
.
In other words, to multiply fractional expressions, multiply the correspond-
ing numerators and denominators.
SECTION 1.D Fractional Expressions 949
EXAMPLE 9
Multiply
x
x
2
2
1
2
3
x
x
1
4
and simplify your answer.
SOLUTION
x
x
2
2
1
2
3
x
x
1
4
(
(
x
x
2
2
1
2
)
)
(
(
3
x
x
1
4
)
)
. ■
In Example 9, we multiplied and then factored and canceled. You can also
factor and cancel before multiplying, as illustrated in the next example.
EXAMPLE 10
x
2
x
6x
3
8
x
x
2
2
3
x
x
6
2
(x
x
2
)(x
3
4)
(
(
x
x
3
2
)
)
(
(
x
x
2
1
)
)
(x
x
4
)(x
1
2)
x
2
x
2x
1
8
■
Division of fractional expressions is also done in the same manner as division
of numerical fractions.
EXAMPLE 11
x
x
2
2
6
x
x
2
9
x
x
2
3
1
x
x
2
2
6
x
x
2
9
x
x
2
3
1
(
(
x
x
2
3
)
)
(
(
x
x
1
3
)
)
(x
x
1
)(x
3
1)
(x
x
3
)(x
2
1)
. ■
Division problems can also be written in fractional form. For instance, 8/2
means 8 2. Similarly, a compound fraction such as
x
x
2
1
4
3
x
x
2
2
(x 1)(3x 4)
x
2
2
(x 1)(x 1)(3x 4)
(x
2
2)(x 1)
Division of Fractional
Expressions
If a, b, c, and d are algebraic expressions, then
a
b
d
c
a
b
d
c
a
b
d
c
.
That is, to divide fractional expressions, invert the divisor and multiply.
means
x
x
2
1
4
3
x
x
2
2
, which is equivalent to
x
x
2
1
4
3
x
x
2
2
.
Consequently, the basic rule for simplifying a compound fraction is:
Invert the denominator and multiply it by the numerator.
EXAMPLE 12
Compute:
(a) (b)
SOLUTION
(a)
16
yz
y
/
2
z
6
/
y
8
3
z
y
3
z
2
1
8
6
y
y
z
2
2
z
6y
y
3
z
z
3
16
8
6
y
2
z
3
y
5
z
4
2
6
y
52
z
43
12y
3
z
(b)
y
y
2
2
y
3
1
y
(y 2)
y
(
2
y
3
y)
(y 2)
y
y
2
(y
2
1)
(y 2)
y
(y
2
1)
■
EXAMPLE 13
Simplify the compound fraction
.
SOLUTION First write the numerator as a single fraction, then invert and mul-
tiply.
x(x
h
h)
1
h
x(x
1
h)
■
x(x
h
h)
h
x
x
(x
(x
h)
h)
h
x(x
x
h)
x(
x
x
h
h)
h
x
1
h
1
x
h
x
1
h
1
x
h
y
y
2
2
y
3
y
y
y
2
2
y
3
y
1
8
6
y
y
z
2
2
z
6y
y
3
z
z
3
950 APPENDIX 1 Algebra Review
2

SECTION 1.D Fractional Expressions 951
EXERCISES 1.D
In Exercises 1–10, express the fraction in lowest terms.
1.
6
4
3
9
2.
1
3
2
3
1
3. 4.
x
x
2
2
4
5.
x
x
2
2
2
x
x
2
1
6.
z
z
3
1
1
7.
a
a
2
3
b
b
2
3
8.
x
4
x
3
3x
2
9. 10.
(x
2
x
y
4
2
)(x
y
2
4
xy)
In Exercises 11–28, perform the indicated operations.
11.
3
7
2
5
12.
7
8
5
6
13.
1
7
9
1
2
1
3
14.
1
a
2
b
a
15.
d
c
3
e
c
16.
r
s
s
t
r
t
17.
b
c
b
c
18.
a
b
2
b
a
2
3
b
a
3
19.
x
1
1
1
x
20.
2x
1
1
2x
1
1
21.
x
1
4
(x
2
4)
2
x
2
8
3
x 16
22.
1
x
x
1
y
x
1
y
2
23.
1
x
3x
1
4
24.
x
3
1
x
4
1
25.
x
1
y
x
x
3
y
y
3
26.
5(x 1)
6
(x 2)
2
3(x 1)
x
2
(x 2)
27.
4x(x 1
1
)(x 2)
3
4(
6
x
x
1
2
)
3
28.
(x
2
x
xy
)(x
y
y)
2
(x
2
2
y
2
)
2
In Exercises 29–42, express in lowest terms.
29.
3
4
1
5
2
1
9
0
30.
1
4
0
5
1
6
4
1
2
31.
3
4
a
a
2
c
c
9
8
a
a
2
c
c
3
4
32.
6
2
x
x
2
y
21
y
xy
33.
1
7
1
x
y
6
1
6
4
y
x
2
3
34.
a
c
b
2
a
c
2
d
b
b
a
c
d
2
35.
3x
2
x
9
x
2
8x
2
9
36.
4
3
x
x
1
1
6
5
2x
x
1
4
0
37.
5y
3
25
y
2
y
2
25
38.
6x
6
x
12
x
8
x
2
2
39.
u
u
1
u
2
u
2
1
40.
t
t
2
2
6
t
t
6
9
t
2
t
2
4t
2
5
5
(x c)(x
2
cx c
2
)
x
4
c
3
x
13
27
22
10
6
4
11
12
41.
4
2
u
u
2
2
4
u
u
v
v
v
v
2
2
8u
2
4
u
2
6
uv
9
v
2
9v
2
42.
2
6
x
x
2
2
3
5
x
x
y
y
2
4
y
y
2
2
x
2
6
x
2
x
y
6x
2
y
y
2
In Exercises 43–60, compute the quotient and express in lowest
terms.
43.
1
5
2
1
4
4
44. 45.
v
u
2
v
w
u
u
2
v
v
46.
(
3
x
x
y
2
)
y
2
3
x
x
2
y
y
z
47. 48.
49.
x
x
2
y
y
x
x
y
y
2
50.
51. 52. 53.
54. 55. 56.
57. 58.
59. (x
1
y
1
)
1
60.
x
(
x
1
y)
y
1
1
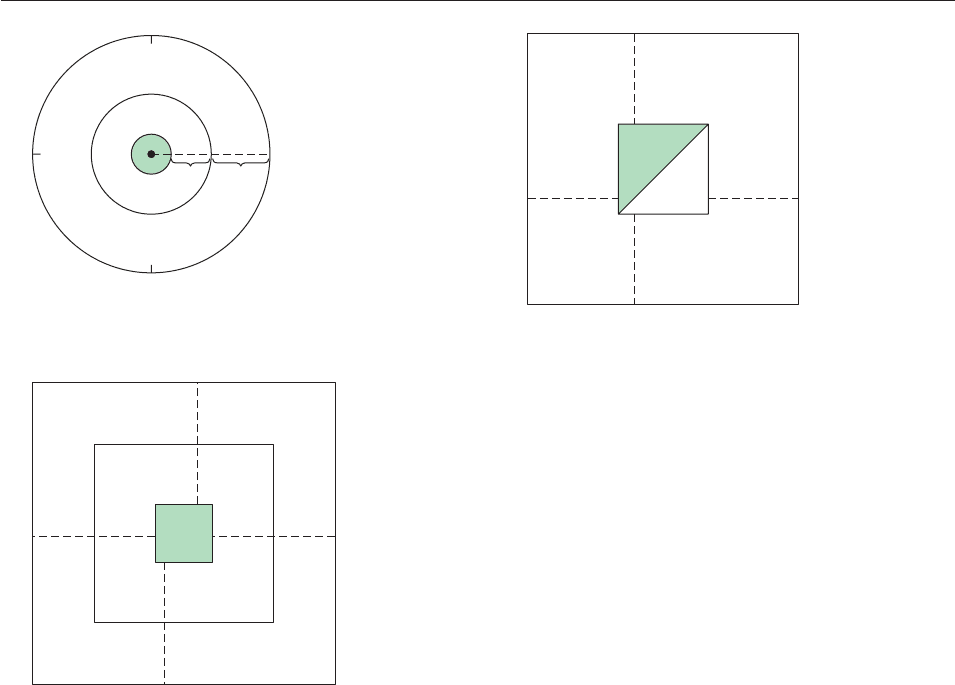
In Exercises 61–64, a dartboard is shown. Assuming that every
dart actually hits the board, find the probability that the dart
will land in the shaded area. This probability is the quotient.
.
61.
x
x
Area of shaded region
Area of dartboard
(x
1
h)
2
x
1
2
h
2x
1
2h
2
1
x
h
3
1
x
4
1
y
6
5
x
2
1
y
6
y
3
1
y
1
1
x
x
1
1
x
1
x
x
1
1
x
1
2
y
1
2
1
x
1
y
1
x
3
2
x
2
2
5
x
(c d)
2
c
2
cd
d
2
u
u
3
2
v
v
3
2
u
2
u
u
v
v
v
2
(
(
x
x
2
2
)
)
2
2
x
x
2
2
2
4
x
x
x
3
4
x
2
x
4
1
5
0
2
0
2
2
7
6
62.
63.
x
x
xx
x
x
xx
x
x
2x 3x
x
952 APPENDIX 1 Algebra Review
64.
ERRORS TO AVOID
In Exercises 65–71, find a numerical example to show that the
given statement is false. Then find the mistake in the statement
and correct it.
65.
1
a
1
b
a
1
b
66.
x
2
x
2
x
6
1 x
3
67.
a
1
b
2
a
1
b
68.
r
r
s
t
1
s
t
69.
u
v
u
v
1 70.
x
1
y
71. (x
y
)
x
1
y
x y
1
x
1
y
x
x
x
xx
x
953
Appendix 2 Geometry Review
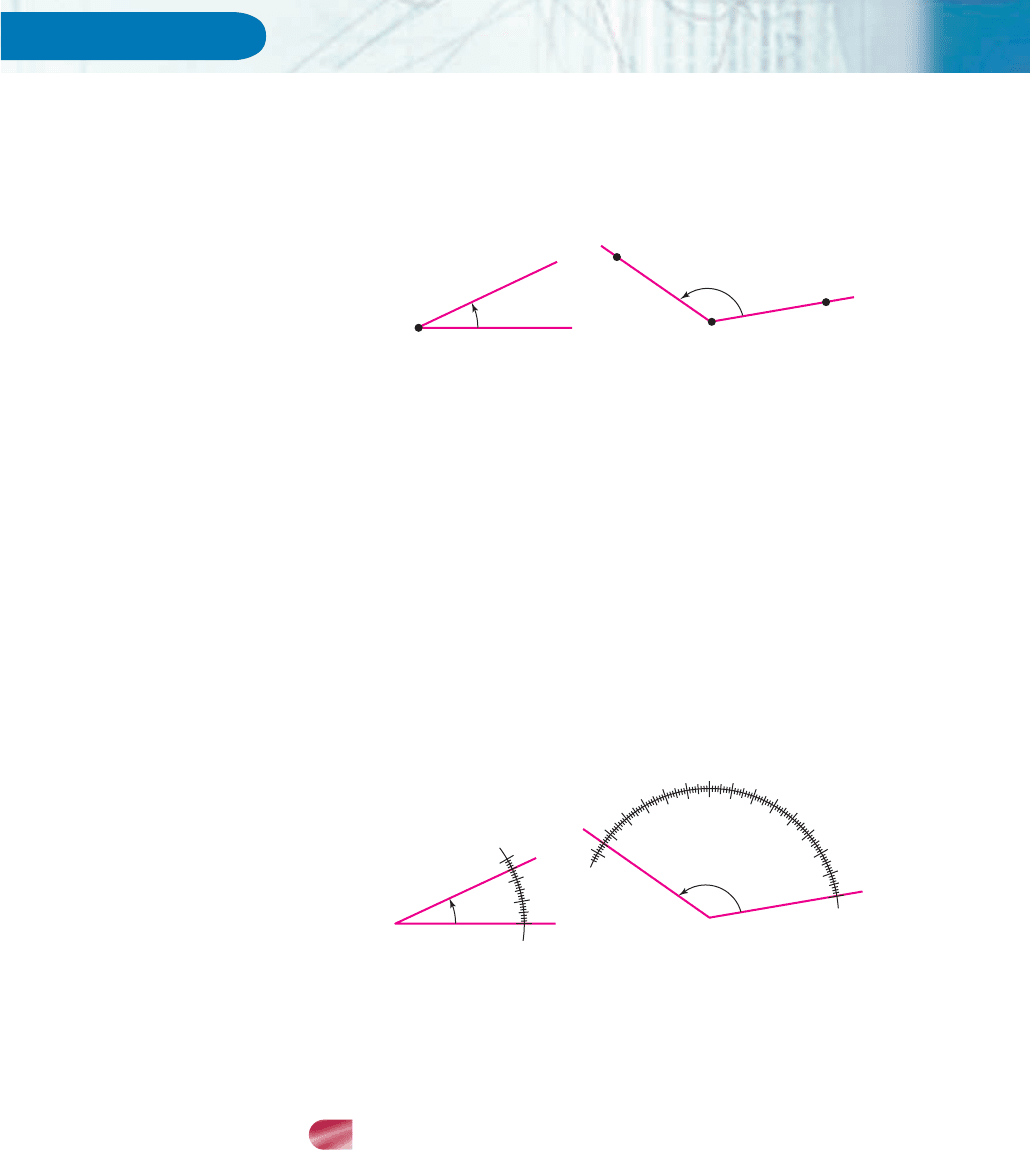
An angle consists of two half-lines that begin at the same point P, as in Figure 1.
The point P is called the vertex of the angle, and the half-lines are called the sides
of the angle.
Figure 1
An angle may be labeled by a Greek letter, such as angle u in Figure 1(a), or by
listing three points (a point on one side, the vertex, a point on the other side), such
as angle QPM in Figure 1(b).
To measure the size of an angle, we must assign a number to each angle. Here
is the classical method for doing this.
1. Construct a circle whose center is the vertex of the angle.
2. Divide the circumference of the circle into 360 equal parts (called degrees)by
marking 360 points on the circumference, beginning with the point where one
side of the angle intersects the circle. Label these points 0°, 1°, 2°, 3°, and so on.
3. The label of the point where the second side of the angle intersects the circle
is the degree measure of the angle.
For example, Figure 2 shows an angle u of measure 25 degrees (in symbols, 25°)
and an angle b of measure 135°.
Figure 2
An acute angle is an angle whose measure is strictly between 0° and 90°,
such as angle u in Figure 2. A right angle is an angle that measures 90°. An
obtuse angle is an angle whose measure is strictly between 90° and 180°, such as
angle b in Figure 2.
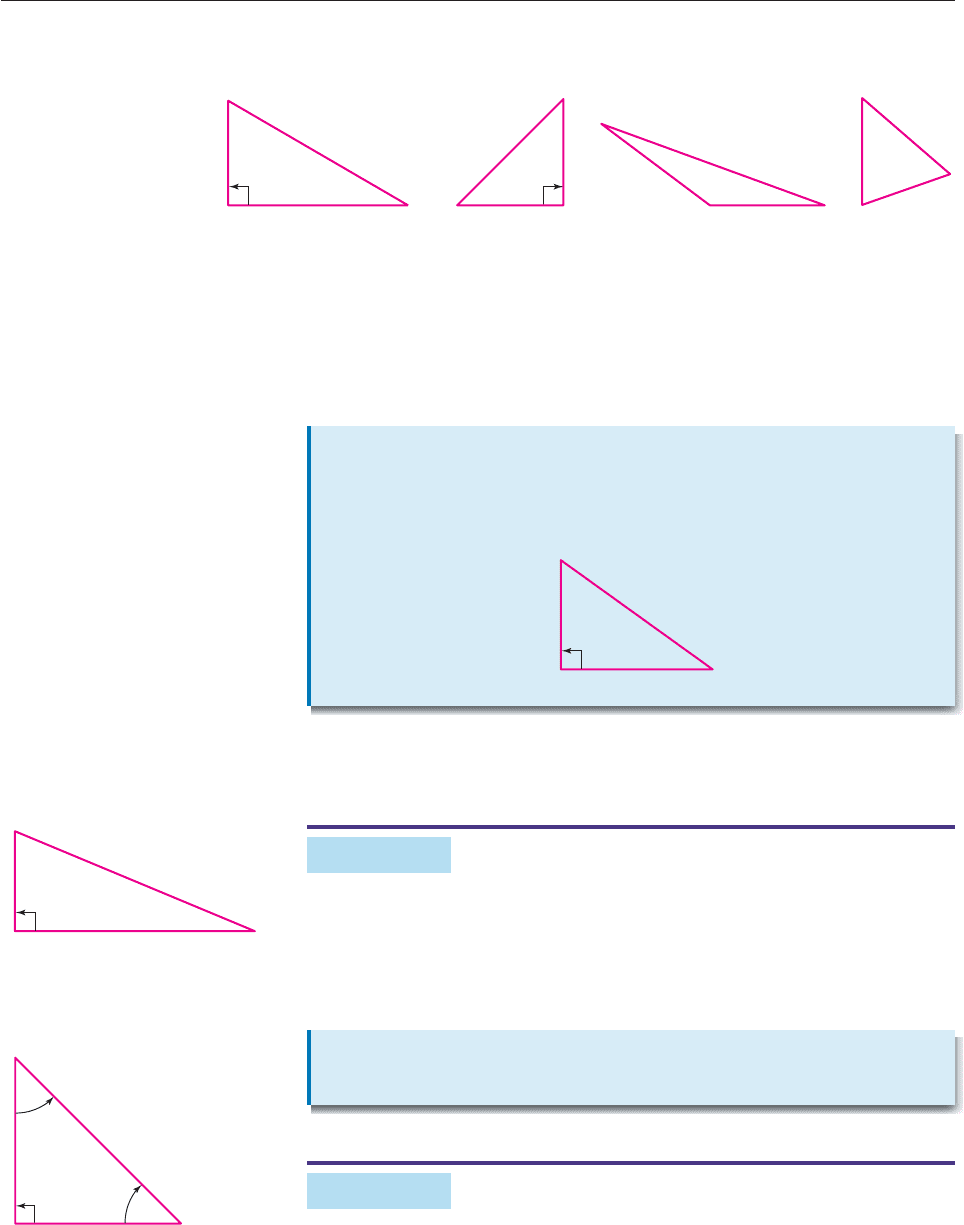
TRIANGLES
A triangle has three sides (straight line segments) and three angles, formed at the
points where the various sides meet. When angles are measured in degrees,
the sum of the measures of all three angles of a triangle is always 180°.
θ
β
30˚
20˚
80˚
90˚
100˚
110˚
120
˚
130
˚
140
˚
70˚
60˚
50˚
40
˚
30
˚
20
˚
10
˚
0
˚
10˚
0˚
(a)
θ
P
(b)
P
Q
M
954 APPENDIX 2 Geometry Review
45°
45°
1
x
A
C
B
For instance, see Figure 3. This fact is proved in Exercise 37.
Figure 3
A right triangle is a triangle, one of whose angles is a right angle, such as the
first two triangles shown in Figure 3. The side of a right triangle that lies opposite
the right angle is called the hypotenuse. In each of the right triangles in Figure 3,
side AC is the hypotenuse.
See Exercise 38 for a proof of the Pythagorean Theorem.
EXAMPLE 1
Consider the right triangle with sides of lengths 5 and 12, as shown in Figure 4.
According to the Pythagorean Theorem, the length c of the hypotenuse satis-
fies the equation c
2
5
2
12
2
25 144 169. Since 169 13
2
, we see that
c must be 13. ■
EXAMPLE 2
Suppose the hypotenuse of the right triangle shown in Figure 5 has length 1 and
that angles B and C measure 45° each.
30°
60°
90°
90°
45°
45° 143°
20°
17°
71°
60°
49°
A
A
B
BCC
Pythagorean
Theorem
If the sides of a right triangle have lengths a and b and the hypotenuse has
length c, then
c
2
a
2
b
2
.
a
b
c
Isosceles
Triangle Theorem
If two angles of a triangle are equal, then the two sides opposite these
angles have the same length.
5
12
c
Figure 4
Figure 5
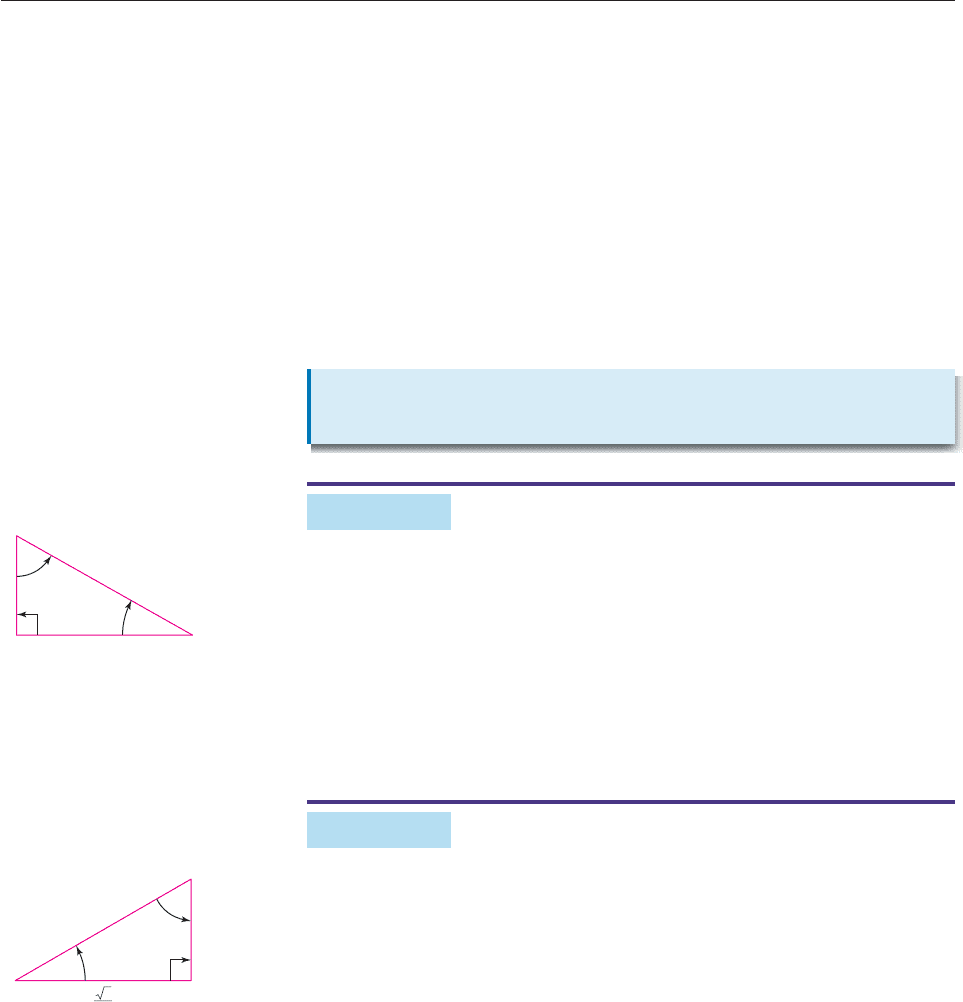
APPENDIX 2 Geometry Review 955
Then by the Isosceles Triangle Theorem, sides AB and AC have the same length.
If x is the length of side AB, then by the Pythagorean Theorem,
x
2
x
2
1
2
2x
2
1
x
2
1
2
x
1
2
1
2
2
2
.
(We ignore the other solution of this equation, namely, x 1/2
, since x rep-
resents a length here and therefore must be nonnegative.) Therefore, the sides of
a 90°45°45° triangle with hypotenuse 1 are each of length 2
/2. ■
EXAMPLE 3
Suppose that in the right triangle shown in Figure 6 angle B is 30° and the length
of hypotenuse BC is 2.
By the 30-60-90 Triangle Theorem, the side opposite the 30° angle, namely,
side AC, has length 1. If x denotes the length of side AB, then by the Pythagorean
Theorem,
1
2
x
2
2
2
x
2
3
x 3
■
EXAMPLE 4
The right triangle shown in Figure 7 has a 30° angle at C, and side AC has length
3
/2.
Let x denote the length of the hypotenuse BC. By the 30-60-90 Triangle The-
orem, side AB has length
1
2
x. By the Pythagorean Theorem,
1
2
x
2
2
3
2
x
2
x
4
2
3
4
x
2
3
4
3
4
x
2
x
2
1
x 1.
Therefore, the triangle has hypotenuse of length 1 and sides of lengths 1/2 and
3
/2. ■
30-60-90
Triangle Theorem
In a right triangle that has an angle of 30°, the length of the side opposite
the 30° angle is one-half the length of the hypotenuse.
30
60
2
B
x
A
C
Figure 6
30
60
x
CA
B
3
2
Figure 7
