Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

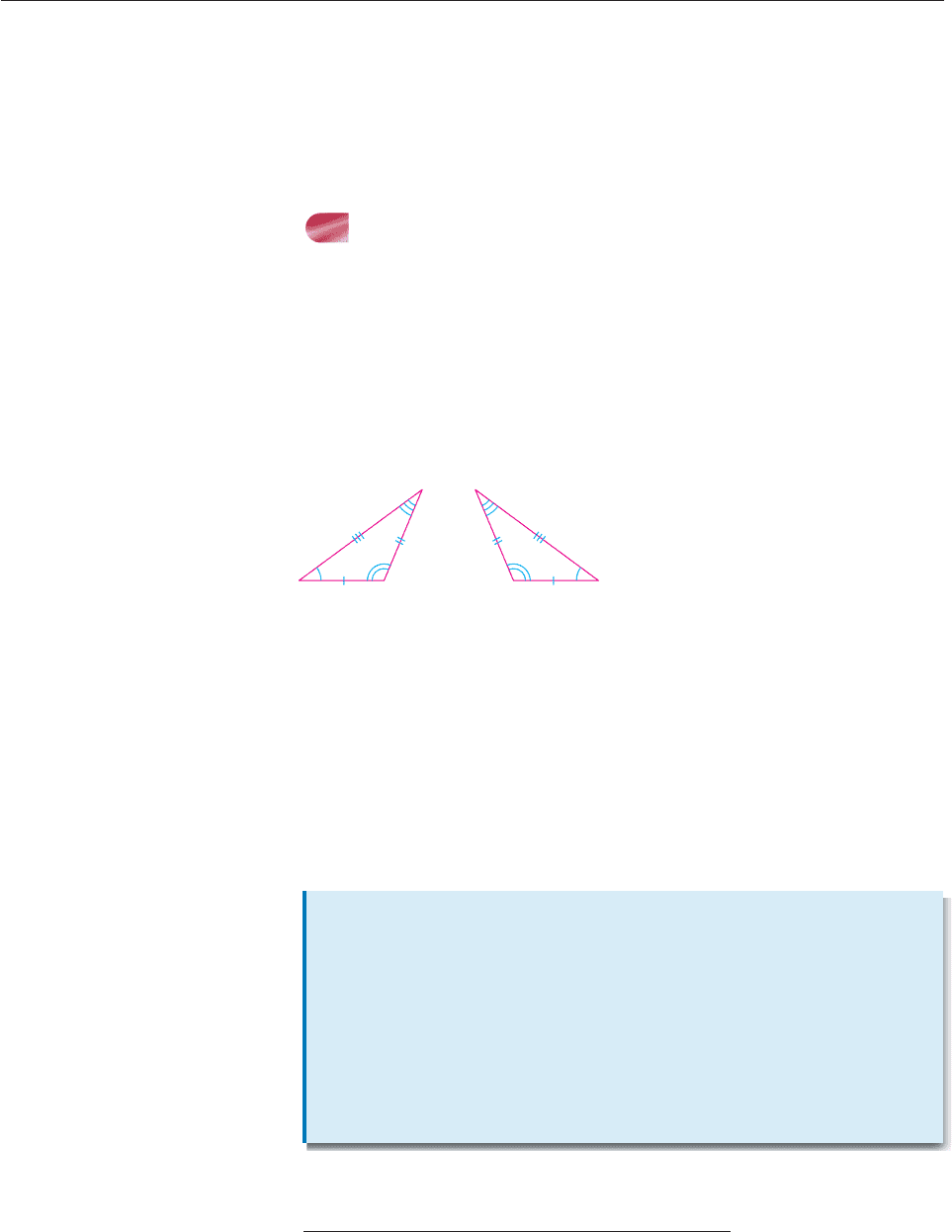
Figures 6 and 7 illustrate properties shared by all triangles.
The longest side of a triangle is always opposite its largest angle.
The shortest side of a triangle is always opposite its smallest angle.
You may find these facts helpful when checking solutions to triangle problems.
CONGRUENT TRIANGLES
Two angles are said to be congruent if they have the same measure, and two line
segments are congruent if they have the same length. We say that two trian-
gles are congruent if the three sides and three angles of one are congruent
respectively to the corresponding sides and angles of the other, as illustrated in
Figure 8.
Figure 8
When two triangles are congruent, you can place one on top of the other so that
they coincide. (You might have to rotate or flip one of the triangles over to do this,
as is the case in Figure 8.) Thus,
Congruent triangles have the same size and same shape.
The key facts about congruent triangles are proved in high school geometry.
B
A
C
D
E
F
AB FE
~~
~
~
~
~
BC ED
CA DF
Congruent Triangles
Corresponding
Congruent Sides
*
⬔A ⬔F
⬔B ⬔E
⬔C ⬔D
Corresponding
Congruent Angles
956 APPENDIX 2 Geometry Review
Congruent
Triangles Theorem
If two triangles are given, then any one of the following conditions guar-
antees that they are congruent.
1. SAS: Two sides and the angle between them in one triangle are congru-
ent to the corresponding sides and angle in the other triangle.
2. ASA: Two angles and the side between them in one triangle are congru-
ent to the corresponding angles and side in the other triangle.
3. SSS: The three sides of one triangle are congruent to the corresponding
sides of the other triangle.
*The symbol means “is congruent to.”

APPENDIX 2 Geometry Review 957
EXAMPLE 5
Show that the right triangles in Figure 9 are congruent.
SOLUTION Triangle ABC has angles of 90° and 34°. Since the sum of all three
angles is 180°, angle A must measure 56°. Hence, we have these congruences.
⬔A ⬔R [Both measure 56°]
⬔B ⬔S [Both measure 90°]
AB RS [Both have length 2]
Since two angles and the side between them in triangle ABC are congruent to the
corresponding angles and side in triangle DEF, the triangles are congruent by
ASA. ■
SIMILAR TRIANGLES
Two triangles are said to be similar if the three angles of one are congruent re-
spectively to the three angles of the other, as illustrated in Figure 10.
Figure 10
Thus,
Similar triangles have the same shape, but not necessarily the same size.
In Figure 10, for example, the sides of triangle DEF are twice as long as the cor-
responding sides of triangle ABC:
d 2a, e 2b, f 2c,
which is equivalent to:
d
a
2,
b
e
2,
c
f
2.
Hence,
d
a
b
e
c
f
.
A similar fact holds in the general case.
C
BD E
F
c
f
d
e
a
b
A
⬔A ⬔D
⬔B ⬔E
⬔C ⬔F
Corresponding
Angles
Similar Triangles
~
~
~
56
2
S
T
R
Figure 9
34
2
CB
A
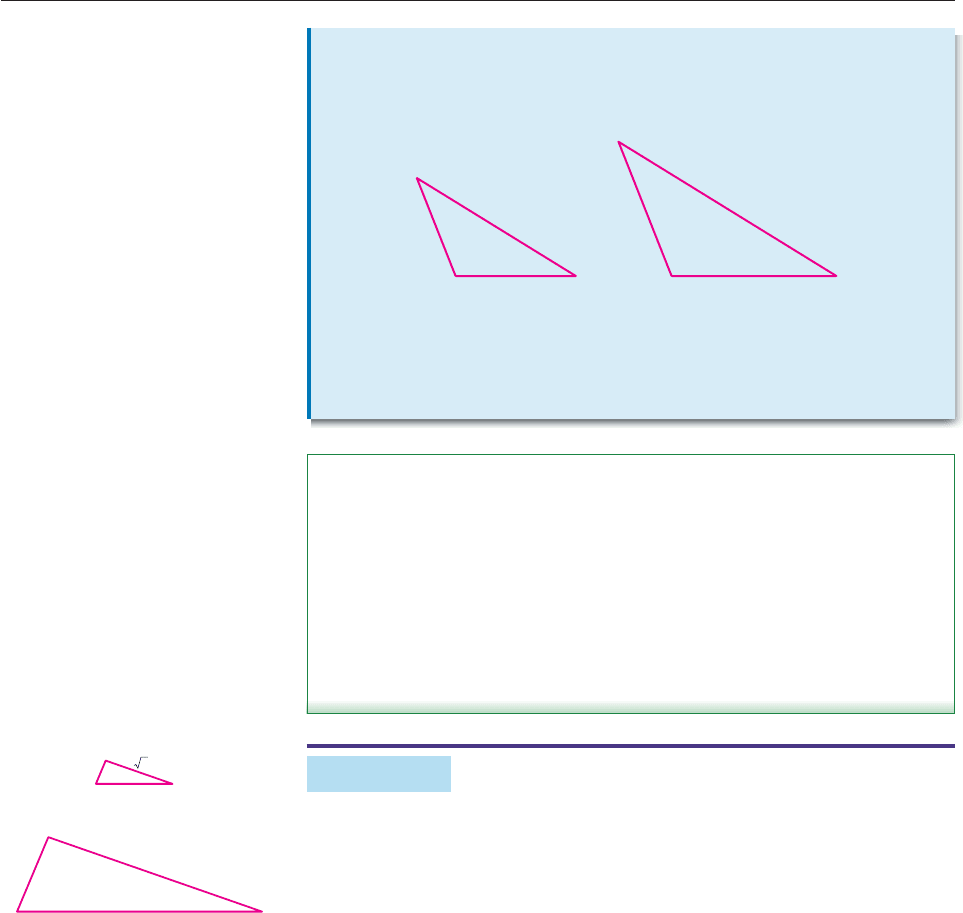
EXAMPLE 6
Suppose the triangles in Figure 11 are similar and that the sides have the lengths
indicated. Find r and s.
SOLUTION By the Ratios Theorem,
l
l
e
e
n
n
g
g
t
t
h
h
D
AC
F
l
l
e
e
n
n
g
g
t
t
h
h
B
E
C
F
.
In other words,
s
8
1
3
0
,
so
3s 10 8
s
1
3
0
8
.
Similarly,
l
l
e
e
n
n
g
g
t
t
h
h
D
AB
E
l
l
e
e
n
n
g
g
t
t
h
h
B
E
C
F
,
958 APPENDIX 2 Geometry Review
Ratios
Theorem
Suppose triangle ABC is similar to triangle DEF (with ⬔A ⬔D;
⬔B ⬔E; ⬔C ⬔F ).
Then the ratios of corresponding sides are equal, that is,
d
a
b
e
c
f
.
F
d
e
f
a
D
E
C
B
c
b
A
NOTE
There are many ways to rewrite the conclusions of the Ratios Theorem. For example,
d
a
c
f
is equivalent to
a
c
d
f
.
To see this, multiply the first equation by
a
f
. Similarly, multiplying by
b
f
shows that
b
e
c
f
is equivalent to
b
c
e
f
.
E
10
F
s
r
D
Figure 11
B
1
3
C
A
8
APPENDIX 2 Geometry Review 959
so
1
r
1
3
0
r
1
3
0
.
Therefore, the sides of triangle DEF are of lengths 10,
1
3
0
, and
1
3
0
8
. ■
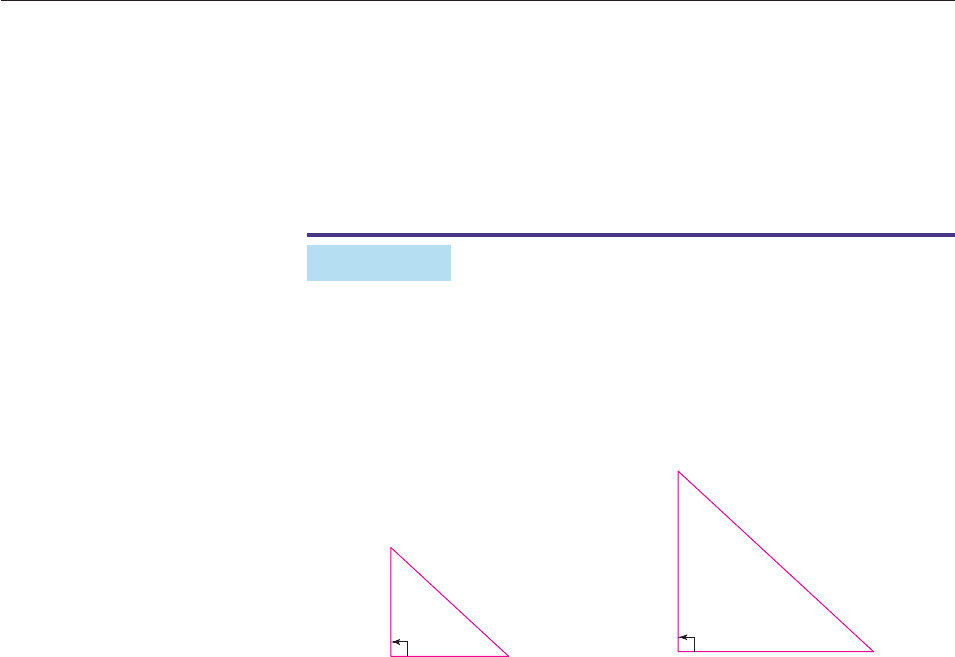
EXAMPLE 7
Tom, who is 6 feet tall, stands in the sunlight near the main library on campus, and
Anne determines that his shadow is 7 feet long. At the same time, their friend Mary
finds that the library casts a 100-foot-long shadow. How high is the main library?
SOLUTION Both Tom and the library are perpendicular to the ground. So we
have the right triangles in Figure 12 (which is not to scale).
Figure 12
Angles B and E each measure 90°; hence,
⬔B ⬔E.
Because the sun hits both Tom and the library at the same angle,
⬔A ⬔D.
If each of these angles measures k°, then angle C measures 180° 90° k°
(because the sum of the angles in triangle ABC must be 180°). Similarly, angle F
must also measure 180° 90° k°, so
⬔C ⬔F.
Therefore, triangle ABC is similar to triangle DEF. By the Ratios Theorem,
l
l
e
e
n
n
g
g
t
t
h
h
D
AB
E
l
l
e
e
n
n
g
g
t
t
h
h
B
E
C
F
6
x
10
7
0
x 6
10
7
0
85.7.
So the library is about 85.7 feet high. ■
In addition to the definition, there are several other ways to show that two
triangles are similar.
CB
A
Shadow
Tom
7
6
FE
D
Shadow
Library
100
x
Example 7 shows why the first condition guarantees similarity: If two pairs of
angles are congruent, then the third angles are also congruent because the sum of the
angles in each triangle is 180°. The proofs of the other conditions will be omitted.
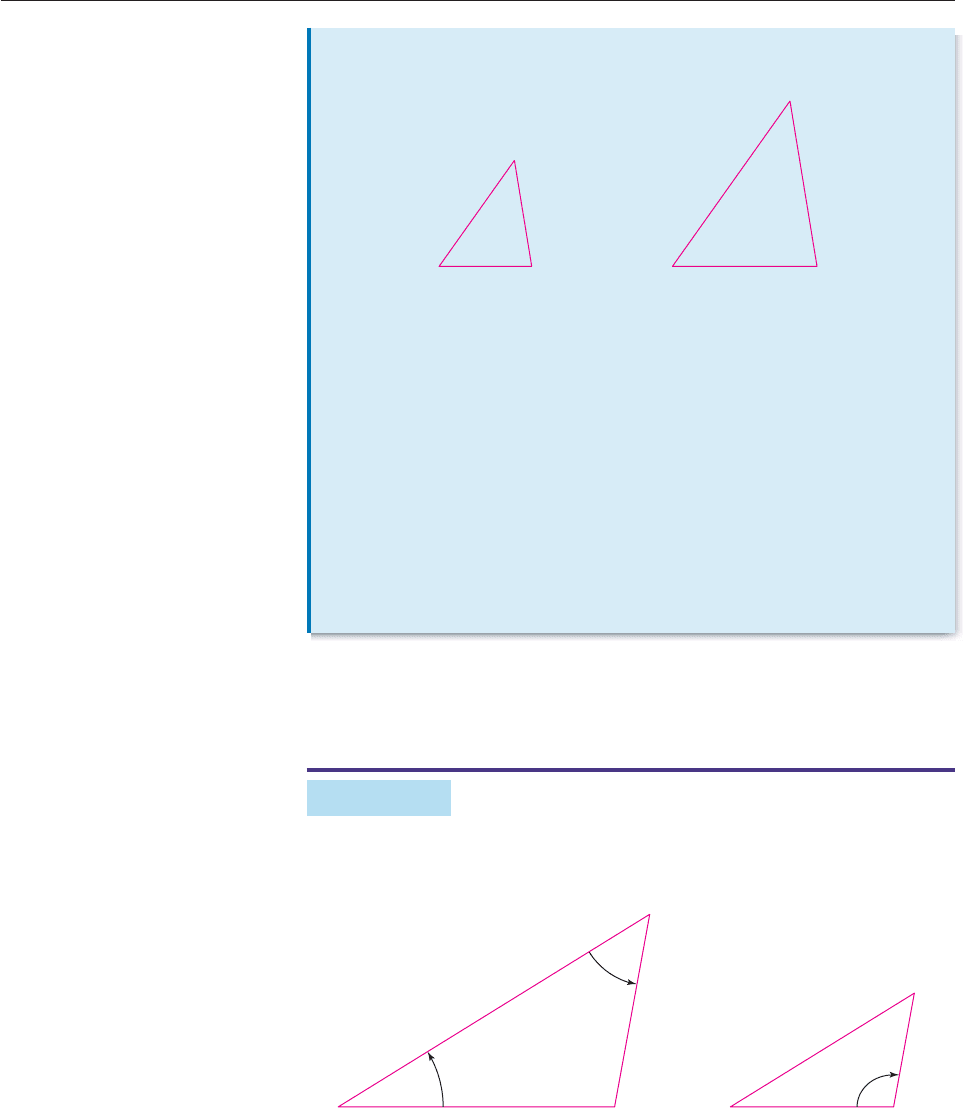
EXAMPLE 8
Show that the triangles in Figure 13 are similar, and find angles C, D, and E and
side f.
Figure 13
SOLUTION Since the sum of the measures of the angles in triangle ABC is
180°, angle C must measure
180° 31.33° 48.67° 100°.
4.58.52
2.7
3.9
6.5
31.33
48.67
100
c
b
C
a
A
D
FE
d
f
e
B
960 APPENDIX 2 Geometry Review
Similar
Triangles
Theorem
Given triangles ABC and DEF,
then any one of the following conditions guarantees that they are similar.
1. AA: Two angles of one are congruent to two angles of the other.
2. S/S/S: The ratios of corresponding sides are all equal:
d
a
b
e
c
f
.
3. S/A/S: An angle in one is congruent to an angle in the other, and the
ratios of the corresponding sides of these angles are the same:
⬔A ⬔D or ⬔B ⬔E or ⬔C ⬔F
b
e
c
f
,
d
a
c
f
d
a
b
e
.
CD F
E
d
f
e
A
B
a
c
b
APPENDIX 2 Geometry Review 961
Hence, ⬔C ⬔F. The ratios of the corresponding sides of these angles are
d
a
3
6
.
.
9
5
.6 and
b
e
2
4
.
.
7
5
.6.
Thus,
⬔C ⬔F and
d
a
b
e
.
Therefore, triangle ABC is similar to triangle DEF by S/A/S of the Similar Trian-
gles Theorem. Consequently, corresponding angles are congruent. In particular,
angle D measures 48.67° and angle E measures 31.33° because ⬔D ⬔A and
⬔E ⬔B. Since corresponding side ratios are equal,
c
f
d
a
8.
f
52
3
6
.
.
9
5
.6
f .6(8.52) 5.112. ■
EXERCISES 2
In Exercises 1–8, find the missing side(s) of the triangle.
1. 2.
3.
4.
5. 6.
60
60
5
b
a
45
5
c
b
30
3
b
a
9
12
c
3
5
a
4
2
b
7.
8.
In Exercises 9 and 10, two congruent triangles are given. Find
the missing sides and angles.
9.
10.
38.21
120
3
5
7
C
T
S
r
t
s
21.79
36.87
53.13
5
4
3
A
t
s
R
r
30
12
c
d
60
10
c
b

In Exercises 11 and 12, prove that the two triangles are con-
gruent.
11.
12.
13. If ⬔u ⬔v and OP OQ, show that PD DO and that
PQ is perpendicular to OD. [Hint: Prove that triangles POD
and QOD are congruent.]
14. If AB AD, BC DC, ⬔x ⬔y, and ⬔u ⬔v, prove that
triangles ADC and ABC are congruent.
D
C
A
B
v
u
y
x
O
P
u
v
Q
D
50 80
6
RS
T
50
6
50
C
B
A
25
65
5
5
4.53
2.11
CB
A
R
S
T
962 APPENDIX 2 Geometry Review
15. If AB DC and ⬔u ⬔v, prove that triangles ABC and
CDA are congruent.
16. If AB CB and ⬔u ⬔v, prove that triangles ABD and
CDB are congruent.
17. If ⬔x ⬔y and ⬔u ⬔v, prove that triangles ABC and
ADC are congruent.
18. If ⬔x ⬔y and ⬔u ⬔v, prove that triangles ABD and
CDB are congruent.
In Exercises 19–22, triangle ABC is similar to triangle RST.
The following notation is used: The side opposite angle A is
denoted a, the side opposite angle B is denoted b, the side
opposite angle R is denoted r, and so on.
19. If ⬔B 37°, ⬔C 90°, a 6, b 4.5 and ⬔R 53°,
⬔T 90°, s 21, find c, r, t.
20. If ⬔A 90°, c 220 and ⬔T 90°, ⬔ S ⬔ B,
r 100, s 50, find a, b, t.
21. If a 7, b 5, c 6, and ⬔A ⬔T, ⬔C ⬔R,
s 2.5, find r and t.
A
D
CB
x
u
v
y
C
A
D
B
x
u
v
y
D
CA
B
u v
D
C
A
B
u
v
APPENDIX 2 Geometry Review 963
22. If a 12, b 9, c 4, and ⬔B ⬔T, ⬔C ⬔R,
t 6.3, find r and s.
In Exercises 23–26, prove that the triangles are similar, and
find the missing sides and angles.
23.
24.
25.
26.
In Exercises 27–30, prove that triangles ABC and RST are
similar, and find the missing sides and angles. The notation
is the same as in Exercises 19–22.
27. ⬔C 90°, a 5, b 5 and ⬔T 90°, r 17.5, s 17.5.
28. ⬔B (160/3)°, ⬔C 90°, a 3.5, b 4.7 and
⬔R (110/3)°, ⬔T 90°, r 7, s 9.4
29. ⬔A 105°, ⬔B 33.5°, a 7, b 4, c 4.8 and
⬔R 105°, ⬔T 33.5°, r 3.5, t 2.
30. ⬔B 25°, ⬔C 142.8°, a 5, b 10, c 14.3, and
⬔S 25°, ⬔T 12.2°, t 10
26.57
CR
B
T
S
s
A
b
41
22
BC
A
S
T
R
6.8857.5
5.25
62.46
75
5
4.59
3.5
65
25
44
65
B
b
C
A
E
d
f
D
F
10.26
22
BC
T
S
15
10
10
10
15
60
A
a
60
R
31. A flagpole casts a 99-foot shadow at the same time as a
5-foot-long stick (perpendicular to the ground) casts a
9-foot shadow. How high is the flagpole?
32. If a 6-foot-tall person casts a 10-foot shadow, how long is
the shadow cast by a 28.3-foot-high tree that is next to the
person?
33. A scale model of a pyramid is 1/20 the size of the original.
If the model pyramid is 4 feet tall, how tall is the original
pyramid?
34. A scale model of a ship is 8 inches long, and its mast is
4.5 inches high. If the real ship is 65 feet long, how high is
the real mast?
35. On a map of Ohio, Columbus is 9.2 centimeters from
Cincinnati and 8.5 centimeters from Marietta. On the map,
Cincinnati is 15.75 centimeters from Marietta. If the actual
distance from Columbus to Cincinnati is 100 miles, how far
is Marietta from Columbus and from Cincinnati?
36. A small mirror is placed on level ground 4 feet from the
base of a flagpole. A person whose eyes are 66 inches above
the ground sees the top of the pole in the mirror when he is
2 feet from the mirror. The base of the pole, the mirror, and
the person are aligned on a straight line. How high is the
flagpole?
THINKERS
37. If ABC is a triangle, prove that the sum of its angles is 180°.
[Hint: In the figure below, use congruent triangles to show
that ⬔u ⬔x and ⬔v ⬔y. You may assume that opposite
sides of a rectangle have the same length.]
38. Prove the Pythagorean Theorem. [Hint: Use the figure
below, in which triangle ABC has a right angle at C. Find
three similar triangles in the figure, and use the properties of
similar triangles to show that a
2
b
2
c
2
.]
A
B
a
b
c x
x
C
F
u
v
x
y
w
D
B
S
C
R
A

964
Each program is preceded by a Description, which describes, in general terms,
how the program operates and what it does. Some programs require that certain
things be done before the program is run (such as entering a function in the
function memory); these requirements are listed as Preliminaries. Occasionally,
italic remarks appear in brackets after a program step; they are not part of the
program but are intended to provide assistance when you are entering the pro-
gram into your calculator. A remark such as “[MATH NUM menu]” means that
the symbols or commands needed for that step of the program are in the NUM
submenu of the MATH menu.
Fraction Conversion for Casio (Built-in on other calculators)
Description: Enter a positive repeating decimal; the program converts it into a
fraction.
Note: When two submenus are given, the first is for 9850 and the second is for
FX 2.0.
Fix 7 [SETUP DISPLAY menu] Then Goto 1 [PROG COM or IF; PROG JUMP menus]
“N ”?N[PROG REL or LOGIC menu] If End [PROG COM or IF menu]
0D (Ans .5)N
Lb1 1 [PROG JUMP menu] Norm [SETUP DISP menu]
D 1D Locate 3, 4, Int N [PROG IO; OPTN NUM menus]
N D Locate 3, 5, “—”
Rnd [OPTN NUM menu] Locate 3, 6, D
If (Frac Ans) 0[PROG COM or IF; OPTN NUM; PROG REL or LOGIC menus]
RREF Program for TI-82 and Casio (Built-in on other calculators)
Preliminaries: Enter a matrix in the matrix memory as matrix A.
Description: When the program is run, it uses row operations to put matrix A
in reduced row echelon form. The reduced matrix is displayed; you may scroll
through it, using the arrow keys. When the program is finished, the original matrix
is in the matrix memory as matrix A, and the reduced matrix is in the matrix
memory as matrix B.
Note: The RREF key on most TI calculators does not work when the matrix has
more rows than columns. This program does work in that situation.
쑺
Appendix 3 Programs

APPENDIX 3 Programs 965
TI
:ClrHome
:[A] [B]
:dim([B]) L
1
:L
1
(1) M
:L
1
(2) N
:1 R
:1 J
:Lbl 6
:abs(seq([B](I, J), I, R, M, 1)) L
2
[LIST menu]
:max(L
2
) T
:If T 0
:Goto 3
:R 1
:Lbl 1
:If abs([B](I, J)) T
:Goto 2
:I 1 I
:Goto 1
:Lbl 2
:
*
row([B](I, J)
1
, [B], I) [B] [MATRIX MATH Menu]
:For(K, 1, I 1, 1)
:
*
row([B](K, J), [B], I, K) [B]
:End
:For(K, I 1, M, 1)
:
*
row([B](K, J), [B], I, K) [B]
:End
:rowswap([B], I, R) [B]
:round([B], 9) [B]
:If R min(M, N)
:Then
:Lbl 7
:Pause round([B], 9)䉴Frac
:Stop
:End
:R 1 R
:J 1 J
:If J N 1
:Goto 7
:Goto 6
:Lbl 3
:J 1 J
:If J N 1
:Goto 7
:Goto 6
Casio
Mat A Mat B
“NUMBER OF ROWS”? M
“NUMBER OF COLUMNS”? N
{M, N} List 3
1 R
1 J
Lbl 6
Mat List(Mat B, J) List 1
seq(List 1[X], X, R, M, 1) List 1 [OPTN LIST menu]
abs(List 1) List 1
Max(List 1) T[OPTN LIST menu]
If T 0
Then Goto 3
If End
R I
Lbl 1
abs(Mat B[I, J]) S
If S T
Then Goto 2
If End
I 1 I
Goto 1
Lbl 2
*
Row Mat B[I, J]
1
, B, I [(MENU) MAT menu]
For 1 K To I 1
*
RowMat B[K, J], B, I, K
Next
For I 1 K To M
*
RowMat B[K, J], B, I, K
Next
Swap B, I, R
If R Min(List 3)
Then Goto 7
Else Goto 8
If End
Lbl 7
Mat B
Stop
Lbl 8
R 1 R
J 1 J
If J N 1
Then Goto 7
If End
쑺
