Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


EXAMPLE 3
Find a formula for the nth term of the geometric sequence {a
n
} that satisfies the
given conditions.
(a) a
1
7 and r 2 (b) a
3
8 and r 1/2
SOLUTION
(a) The equation in the preceding box shows that
a
n
r
n1
a
1
2
n1
7.
(b) We must first find a
1
.
a
n
r
n1
a
1
Let n 3: a
3
r
31
a
1
Substitute a
3
8 and r 1/2: 8
1
2
2
a
1
8
1
4
a
1
Multiply both sides by 4: 32 a
1
.
Therefore,
a
n
r
n1
a
1
1
2
n1
32. ■
EXAMPLE 4
Find a formula for the nth term of the geometric sequence whose first two terms
are 2 and 2/5.
SOLUTION The common ratio is
r
a
a
2
1
2
2
/5
5
2
1
2
1
5
.
Using the equation in the box, we now see that the formula for the nth term is
a
n
r
n1
a
1
1
5
n1
(2)
(
(1
5
)
n
)
n
1
1
(2)
(5
2
)
n1
.
So, the sequence begins 2, 2/5, 2/5
2
, 2/5
3
, 2/5
4
, . . . . ■
EXAMPLE 5
Find a formula for the nth term of the geometric sequence {a
n
} in which
a
2
20/9 and a
5
160/243.
SOLUTION By the equation in the box above, we have
16
2
0
0
/
/
2
9
43
a
a
5
2
r
r
4
a
a
1
1
r
3
.
846 CHAPTER 12 Discrete Algebra

Consequently,
r
3
16
2
0
0
/
/
2
9
43
3
1
2
6
4
0
3
2
9
0
3
8
24
3
9
3
2
8
7
2
3
.
Since a
2
ra
1
, we see that
a
1
a
r
2
2
2
0
/
/
3
9
2
9
0
3
2
1
3
0
.
Therefore,
a
n
r
n1
a
1
2
3
n1
1
3
0
5
2
3
n
. ■
PARTIAL SUMS
If the common ratio r of a geometric sequence is the number 1, then we have
a
n
1
n1
a
1
for every n 1.
Therefore, the sequence is just the constant sequence a
1
, a
1
, a
1
, . . . . For any pos-
itive integer k, the kth partial sum of this constant sequence is
a
1
a
1
a
1
ka
1
144424443
k terms
In other words, the kth partial sum of a constant sequence is just k times the con-
stant. If a geometric sequence is not constant (that is, r 1), then its partial sums
are given by the following formula.
Proof If S denotes the kth partial sum, then the formula for the nth term of a
geometric sequence shows that
S a
1
a
2
a
k
a
1
a
1
r a
1
r
2
a
1
r
3
a
1
r
k1
.
Use this equation to compute S rS.
S a
1
a
1
r a
1
r
2
a
1
r
3
a
1
r
k1
rS a
1
r a
1
r
2
a
1
r
3
a
1
r
k1
a
1
r
k
S rS a
1
a
1
r
k
(1 r)S a
1
(1 r
k
).
Since r 1, we can divide both sides of this last equation by 1 r to complete
the proof.
S
a
1
(
1
1
r
r
k
)
a
1
1
1
r
r
k
. ■
2
n
5
3
n
2
n1
2
5
3
n1
3
SECTION 12.3 Geometric Sequences 847
Partial Sums of a
Geometric Sequence
The kth partial sum of the geometric sequence {a
n
} with common ratio
r 1 is
k
n1
a
n
a
1
1
1
r
r
k
.

EXAMPLE 6
Find the sum
3
2
3
4
3
8
1
3
6
3
3
2
6
3
4
1
3
28
2
3
56
5
3
12
.
SOLUTION Note that this is the ninth partial sum of the geometric sequence
3
2
1
n
. The common ratio is r 1/2. The formula in the box shows that
9
n1
3
2
1
n
a
1
1
1
r
r
9
2
3
1
1
(
(
1
1
/
/
2
2
)
)
9
2
3
1
3/
1
2
/2
9
2
3
2
3
1
2
1
9
1
2
1
9
1
5
1
12
5
5
1
1
3
2
.
The sum can also be found with a calculator (Figure 12–14) and expressed in frac-
tional form.* ■
EXAMPLE 7
A superball is dropped from a height of 9 feet. It hits the ground and bounces to a
height of 6 feet. It continues to bounce up and down. On each bounce, it rises
to 2/3 of the height of the previous bounce. How far has the ball traveled (both up
and down) when it hits the ground for the seventh time?
SOLUTION We first consider how far the ball travels on each bounce. On the
first bounce, it rises 6 feet and falls 6 feet for a total of 12 feet. On the second
bounce, it rises and falls 2/3 of the previous height and hence travels 2/3 of
12 feet. If a
n
denotes the distance traveled on the nth bounce, then
a
1
12, a
2
2
3
a
1
, a
3
2
3
a
2
2
3
2
a
1
,
and in general
a
n
2
3
a
n1
2
3
n1
a
1
.
So {a
n
} is a geometric sequence with common ratio r 2/3. When the ball hits
the ground for the seventh time, it has completed six bounces. Therefore, the total
distance it has traveled is the distance it was originally dropped (9 feet) plus the
distance traveled in six bounces, namely,
9 a
1
a
2
a
3
a
4
a
5
a
6
9
6
n1
a
n
9 a
1
1
1
r
r
6
9 12
1
1
(
(
2
2
/
/
3
3
)
)
6
41.84 feet. ■
848 CHAPTER 12 Discrete Algebra
*For fractional form on TI, use the Frac key, as in Figure 12–14. On HP-39gs, change the number format
in the MODE menu to “fraction.” On Casio 9850, use the Frac program in the Program Appendix.
Figure 12–14

EXAMPLE 8*
When a patient is given a 20 mg dose of aminophylline, the amount of the drug in
the bloodstream t hours later is given by
C(t) 20e
.1155t
.
†
Suppose that a 20 mg dose is given every four hours. Let {b
n
} be the sequence with
b
n
the total amount of aminophylline in the bloodstream after the nth dose.
(a) Find a formula for the nth term of the sequence {b
n
}.
(b) Find the total amount of aminophylline in the bloodstream after 7 doses.
SOLUTION
(a) First, consider what happens to a single dose. The initial amount is C(0)
20 mg. The amount after 4 hours is
C(4) 20e
.1155(4)
20e
.462
12.60 mg.
Similarly, the amounts after 8, 12, and 16 hours, respectively, are
C(8) C(4 2) 20e
.1155(4)(2)
20[e
.1155(4)
]
2
20[e
.462
]
2
7.94 mg
C(12) C(4 3) 20e
.1155(4)(3)
20[e
.1155(4)
]
3
20[e
.462
]
3
5.00 mg
C(16) C(4 4) 20e
.1155(4)(4)
20[e
.1155(4)
]
4
20[e
.462
]
4
3.15 mg.
So the amount of the drug in the bloodstream from a single dose decreases
slowly over time.
When a dose is given every four hours, the amount of the drug in the blood-
stream after each new dose is 20 mg from the new dose plus the amounts
remaining from all of the earlier doses. The following chart describes the situation.
Amount of Drug in bloodstream at time t from each dose
Time Dose 1 Dose 2 Dose 3 Dose 4
t 020
t 420e
.462
20
t 4 2 20[e
.462
]
2
20e
.462
20
t 4 3 20[e
.462
]
3
20[e
.462
]
2
20e
.462
20
.....
.....
.....
Each column shows the amount of a particular dose that remains at the
given time. The sum of each row is the total amount in the bloodstream at
the given time. Summing each row from right to left, we see that
b
1
20 [Amount after 1
st
dose (t 0)]
b
2
20 20e
.462
[Amount after 2
nd
dose (t 4
1)]
b
3
20 20e
.462
20[e
.462
]
2
[Amount after 3
rd
dose (t 4
2)]
b
4
20 20e
.462
20[e
.462
]
2
20[e
.462
]
3
[Amount after 4
th
dose (t 4
3)]
SECTION 12.3 Geometric Sequences 849
*Our thanks to Theresa Laurent of the St. Louis College of Pharmacy for providing data and other
helpful information for this example and several related exercises.
†
We assume that the drug is administered intravenously and that the entire dose enters the bloodstream
immediately.

The same pattern continues, so the amount after the nth dose [when
t 4
(n 1)] is
b
n
20 20e
.462
20[e
.462
]
2
20[e
.462
]
3
20[e
.462
]
n1
If you look carefully at b
n
, you see that it is the nth partial sum of the geo-
metric series with a
1
20 and r e
.462
. By the partial sum formula,
b
n
a
1
1
1
r
r
n
20
1
1
(e
e
.
.
4
4
6
6
2
2
)
n
20
1
1
e
e
.
.
4
4
6
6
2
2
n
.
(b) To find the amount in the bloodstream after 7 doses, we use the preceding for-
mula to compute b
7
.
b
n
20
1
1
e
e
.
.
4
4
6
6
2
2
n
Let n 7: b
7
20
1
1
e
e
.4
.
6
4
2
6
(
2
7)
51.927 mg. ■
850 CHAPTER 12 Discrete Algebra
EXERCISES 12.3
In Exercises 1–12, determine whether the sequence is arith-
metic, geometric, or neither.
1. 2, 7, 12, 17, 22, . . . 2. 2, 6, 18, 54, 162, . . .
3. 13, 13/2, 13/4, 13/8, . . .
4. 1,
1
2
, 0,
1
2
, . . . 5. 50, 48, 46, 44, . . .
6. 2, 3, 9/2, 27/4, 81/8, . . .
7. 3, 3/2, 3/4, 3/8, 3/16, . . .
8. 6, 3.7, 1.4, .9, 3.2, . . .
9. 3, 32
, 6, 62
, 12, 122
, . . .
10. ln e, ln e
2
, ln e
3
, ln e
4
, ln e
5
, . . .
11. 6, 6, 6, 6, 6, . . .
12. 1,
3
3
,
3
9
, 3, 3
3
3
, 3
3
9
, 9, . . .
In Exercises 13–22, one term and the common ratio r of a geo-
metric sequence are given. Find the sixth term and a formula
for the nth term.
13. a
1
5, r 2 14. a
1
1, r 2
15. a
1
4, r
1
4
16. a
1
6, r
2
3
17. a
1
10, r
1
2
18. a
1
p, r
1
5
19. a
2
12, r 1/3 20. a
3
1/2, r 3
21. a
4
4/5, r 2/5 22. a
5
2/3, r 1/3
In Exercises 23–30, show that the given sequence is geometric
and find the common ratio.
23.
1
2
n
24. {2
3n
}
25. {5
n2
} 26. {3
n/2
}
27. {(5
)
n
} 28. {4
n4
}
29. {10e
.4n
} 30. {5e
.5n
}
In Exercises 31–38, use the given information about the geo-
metric sequence {a
n
} to find a
5
and a formula for a
n
.
31. a
1
256, a
2
64 32. a
1
1/6, a
2
1/18
33. a
1
1/2, a
2
5 34. a
1
7
, a
2
42
35. a
3
4, a
6
1/16 36. a
3
4, a
6
32
37. a
1
5, a
7
20 (assume that r 0)
38. a
2
6, a
7
192
In Exercises 39–42, find the kth partial sum of the geometric
sequence {a
n
} with common ratio r.
39. k 6, a
1
5, r
1
2
40. k 8, a
1
9, r
1
3
41. k 7, a
2
6, r 2 42. k 9, a
2
6, r
1
4
In Exercises 43–48, find the sum.
43.
7
n1
2
n
44.
6
k1
3
1
2
k
45.
9
n1
1
3
n
46.
5
n1
5
3
n1
47.
6
j1
4
3
2
j1
48.
8
t1
6(.9)
t1

In Exercises 49–54, you are asked to find a geometric sequence.
In each case, round the common ratio r to four decimal places.
49. The number of students per computer in U.S. schools in
year n (with n 1 corresponding to 1997) can be approxi-
mated by a geometric sequence whose first two terms are
a
1
5.912 and a
2
5.687.*
(a) Find a formula for a
n
.
(b) What is the number of students per computer in 2007?
(c) In what year will there first be fewer than 3 students per
computer?
50. According to data from the U.S. Census Bureau, the popu-
lation of the United States (in millions) in year n can be
approximated by a geometric sequence {b
n
}, where n 1
corresponds to 2001.
(a) If b
1
285.108 and b
3
290.850, find a formula for b
n
.
(b) Estimate the U.S. population in 2008 and 2011.
51. The value of all group life insurance (in billions of dollars)
in year n can be approximated by a geometric sequence
{c
n
}, where n 1 corresponds to 1991.
†
(a) If there was $3.9631 billion in effect in 1991 and
$4.1672 billion in 1992, find a formula for c
n
.
(b) How much group life insurance is in effect in 2000? In
2004? In 2008?
52. Data from the U.S. Centers for Disease Control and Preven-
tion indicate that the number of newly reported cases of
AIDs each year can be approximated by a geometric
sequence {a
n
}, where n 1 corresponds to 2000.
(a) If there were 40,758 cases reported in 2000 and 41,573
cases reported in 2001, find a formula for a
n
.
(b) About how many cases were reported in 2004?
(c) Find the total number of cases reported from 2000 to
2007 (inclusive).
53. The amount spent per person per year on cable and satellite
TV can be approximated by a geometric sequence {b
n
},
where n 1 corresponds to 2001.
‡
(a) If $204.74 was spent in 2001 and $232.22 was spent in
2003, find a formula for b
n
.
(b) Find the total that will be spent per person from 2001 to
2009 (inclusive).
54. According to data from the U.S. National Center for Educa-
tion Statistics, the number of bachelor’s degrees earned by
women can be approximated by a geometric sequence {c
n
},
where n 1 corresponds to 1996.
(a) If 642,000 degrees were earned in 1996 and 659,334 in
1997 find a formula for c
n
.
(b) How many degrees were earned in 2000? In 2002? In
2005?
SECTION 12.3 Geometric Sequences 851
(c) Find the total number of degrees earned from 1996 to
2005.
55. A ball is dropped from a height of 8 feet. On each bounce, it
rises to half its previous height. When the ball hits the
ground for the seventh time, how far has it traveled?
56. A ball is dropped from a height of 10 feet. On each bounce,
it rises to 45% of its previous height. When it hits the
ground for the tenth time, how far has it traveled?
57. In Example 8, suppose a 20 mg dose of aminophylline is given
to a patient every 5 hours. Let c
n
denote the total amount of
aminophylline in the patient’s bloodstream after the nth dose.
(a) Find a formula for the nth term of the sequence {c
n
}.
(b) How much aminophylline is in the bloodstream after
the 9
th
dose?
58. When a patient is given a 300 mg dose of the drug cimetidine,
the amount of the drug remaining in the bloodstream t hours
later is given by C(t) 300 e
.3466t
. Suppose the patient
receives a 300 mg dose every three hours and d
n
denotes the
total amount of cimetidine in the bloodstream after n doses.
(a) Find a formula for the nth term of the sequence {d
n
}.
(b) How much cimetidine is in the patient’s bloodstream
after the 8
th
dose?
59. If you are paid a salary of 1¢ on the first day of March and
2¢ on the second day, and your salary continues to double
each day, how much will you earn in the month of March?
60. Starting with your parents, how many ancestors do you have
for the preceding ten generations?
61. A car that sold for $8000 depreciates in value 25% each
year. What is it worth after five years?
62. A vacuum pump removes 60% of the air in a container at
each stroke. What percentage of the original amount of air
remains after six strokes?
THINKERS
63. Suppose {a
n
} is a geometric sequence with common ratio
r 0 and each a
n
0. Show that the sequence {log a
n
} is
an arithmetic sequence with common difference log r.
64. Suppose {a
n
} is an arithmetic sequence with common differ-
ence d. Let C be any positive number. Show that the sequence
{C
a
n
} is a geometric sequence with common ratio C
d
.
65. In the geometric sequence 1, 2, 4, 8, 16, . . . , show that each
term is 1 plus the sum of all preceding terms.
66. In the geometric sequence 2, 6, 18, 54, . . . , show that each
term is twice the sum of 1 and all preceding terms.
67. The minimum monthly payment for a certain bank credit
card is the larger of 1/25 of the outstanding balance or $5.
If the balance is less than $5, the entire balance is due. If
you make only the minimum payment each month, how
long will it take to pay off a balance of $200 (excluding any
interest that might be due)?
*Based on data from Quality Education Data, Inc.
†
Based on data from the American Council of Life Insurance.
‡
Based on data and projections in the Statistical Abstract of the United
States: 2007.

852 CHAPTER 12 Discrete Algebra
■ Find the sum of an infinite geometric series.
■ Use geometric series to set up and solve applied problems.
An infinite series (or simply series) is an expression of the form
a
1
a
2
a
3
a
4
a
5
,
where each a
n
is a real number. This notation suggests the “sum” of the infinite
sequence a
1
, a
2
, a
3
, a
4
, a
5
, . . . However, ordinary addition is defined only for a
finite list of numbers. So we must define what is meant by the sum of an infinite
series. Consider, for example, the infinite series
1
3
0
1
3
0
2
1
3
0
3
1
3
0
4
.
We begin with the sequence 3/10, 3/10
2
, 3/10
3
, 3/10
4
, . . . and compute its par-
tial sums.
S
1
1
3
0
,
S
2
1
3
0
1
3
0
2
1
3
0
3
0
,
S
3
1
3
0
1
3
0
2
1
3
0
3
1
3
0
3
0
3
0
,
S
4
1
3
0
1
3
0
2
1
3
0
3
1
3
0
4
1
3
0
3
,0
3
0
3
0
.
These partial sums S
1
, S
2
, S
3
, S
4
, . . . themselves form a sequence.
1
3
0
,
1
3
0
3
0
,
1
3
0
3
0
3
0
,
1
3
0
3
,0
3
0
3
0
, . . . .
The terms in the sequence of partial sums appear to be getting closer and closer to
1/3. In other words, as k gets larger and larger, the corresponding partial sum S
k
gets closer and closer to 1/3. So we say that 1/3 is the sum of the infinite series
1
3
0
1
3
0
2
1
3
0
3
1
3
0
4
,
or that this series converges to 1/3, and we write
1
3
0
1
3
0
2
1
3
0
3
1
3
0
4
1
3
.
The general case is handled similarly. If a
1
a
2
a
3
a
4
is an infi-
nite series, then its partial sums are the numbers
S
1
a
1
,
S
2
a
1
a
2
,
S
3
a
1
a
2
a
3
,
12.3.A SPECIAL TOPICS Infinite Series
Section Objectives

and in general, for any k 1,
S
k
a
1
a
2
a
3
a
4
a
k
.
If it happens that the terms S
1
, S
2
, S
3
, S
4
, . . . of the sequence of partial sums get
closer and closer to a particular real number S in such a way that the partial sum
S
k
is arbitrarily close to S when k is large enough, then we say that the series con-
verges and that S is the sum of the convergent series.
Not every series has a sum. For instance, the partial sums of the series
1 2 3 4
get larger and larger and never get closer and closer to a single real number. So
this series is not convergent and does not have a sum.
EXAMPLE 1
Although no proof will be given here, it is clear that every infinite decimal may be
thought of as the sum of a convergent series. For instance,
p 3.1415926 3 .1 .04 .001 .0005 .00009 .
Note that the third partial sum is 3 .1 .04 3.14, which is p to two dec-
imal places. Similarly, the kth partial sum of this series is just p to k 1 decimal
places. ■
INFINITE GEOMETRIC SERIES
If {a
n
} is a geometric sequence with common ratio r, then the corresponding infi-
nite series
a
1
a
2
a
3
a
4
a
5
is called an infinite geometric series. By using the formula for the nth term of a
geometric sequence, we can also express the corresponding geometric series in
the form
a
1
ra
1
r
2
a
1
r
3
a
1
r
4
a
1
.
Under certain circumstances, an infinite geometric series is convergent and has a
sum.
Although we cannot prove this fact rigorously here, we can make it highly plausi-
ble both geometrically and algebraically.
SPECIAL TOPICS 12.3.A Infinite Series 853
Sum of an Infinite
Geometric Series
If r 1, then the infinite geometric series
a
1
ra
1
r
2
a
1
r
3
a
1
r
4
a
1
converges, and its sum is
1
a
1
r
.
EXAMPLE 2
8
5
5
8
2
5
8
3
is an infinite geometric series with a
1
8/5 and r 1/5.
The kth partial sum of this series is the same as the kth partial sum of the sequence
{8/5
n
}, and hence, from the box on p. 847, we know that
S
k
a
1
1
1
r
r
k
8
5
8
5
8
5
5
4
1
5
1
k
2
1
5
1
k
2
5
2
k
.
The function f (x) 2 2/5
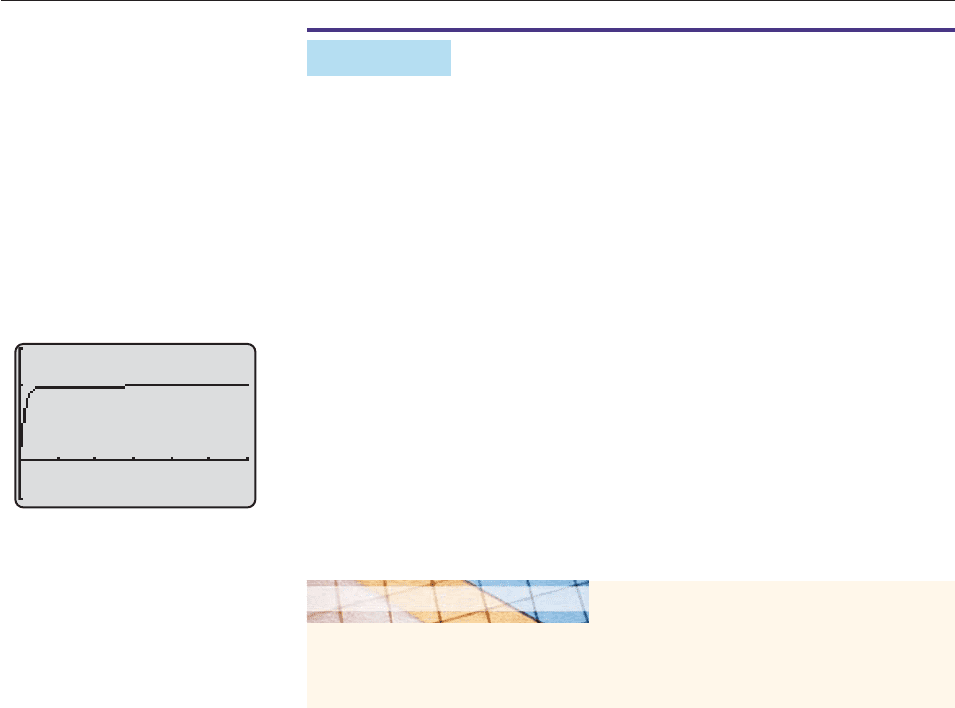
x
is defined for all real numbers. When x k is a pos-
itive integer, then f (k) is S
k
, the kth partial sum of the series. Using a calculator,
we obtain the graph of f (x) in Figure 12–15.
Your calculator will probably tell you that every partial sum is 2, once you move
beyond approximately x 15. Actually, the partial sums are slightly smaller than
2 but are rounded to 2 by the calculator. In any case, the horizontal line through 2
is a horizontal asymptote of the graph (meaning that the graph gets very close to
the line as x gets larger), so it is very plausible that the sequence converges to the
number 2. But 2 is exactly what the preceding box says the sum should be.
1
a
1
r
8
4
2. ■
Example 2 is typical of the general case, as can be seen algebraically. Con-
sider the geometric series a
1
a
2
a
3
with common ratio r such that
r 1. The kth partial sum S
k
is the same as the kth partial sum of the geometric
sequence {a
n
}, and hence,
S
k
a
1
1
1
r
r
k
.
As k gets larger and larger, the number r
k
gets very close to 0 because r 1 (for
instance, (.6)
20
.0000366 and .2
9
.000000512). Consequently, when k is
very large, 1 r
k
is very close to 1 0 so that
S
k
a
1
1
1
r
r
k
is very close to a
1
1
1
0
r
1
a
1
r
.
8
5
4
5
8
5
1
1
5
1
5
1
k
4
5
1
1
5
k
1
1
5
854 CHAPTER 12 Discrete Algebra
Graph f (x) in the same viewing window as in Figure 12–15. Use the trace feature to
move the cursor along the graph. As x gets larger, what is the apparent value of f (x)
(that is, the value of the partial sum)?
GRAPHING EXPLORATION
−1
030
3
Figure 12–15

EXAMPLE 3
1
2
1
4
1
8
1
1
6
is an infinite geometric series with a
1
1/2 and
r 1/2. Since r 1, this series converges, and its sum is
1
a
1
r
1
3
. ■
Infinite geometric series provide another way of writing an infinite repeating
decimal as a rational number.
EXAMPLE 4
To express 6.8573573573
as a rational number, we first write it as
6.8 .0573573573 . Consider .0573573573 as an infinite series.
.0573 .0000573 .0000000573 .0000000000573 ,
which is the same as
.0573 (.001)(.0573) (.001)
2
(.0573) (.001)
3
(.0573) .
This is a convergent geometric series with a
1
.0573 and r .001. Its sum is
1
a
1
r
1
.
05
.
7
0
3
01
.0
.9
5
9
7
9
3
9
5
9
7
9
3
0
.
Therefore,
6.8573573573 6.8 [.0573 .0000573 ]
6.8
9
5
9
7
9
3
0
6
1
8
0
9
5
9
7
9
3
0
6
9
8
9
,5
9
0
0
5
4
6
5
6
6
6
7
. ■
EXAMPLE 5
Suppose a patient is given a 20 mg dose of aminophylline every four hours, as in
Example 8 of Section 12.3. Does the total amount of aminophylline in the blood-
stream eventually level off? If so, what is this steady state amount?
SOLUTION As we saw in Example 8(a), the total amount of aminophylline in
the patient’s bloodstream after n doses is
b
n
20 20e
.462
20[e
.462
]
2
20[e
.462
]
3
20[e
.462
]
n1
.
Each new dose adds another term to this sum. So if the doses are continued for a
long time, the total amount will be approximately given by the geometric series
20 20e
.462
20[e
.462
]
2
20[e
.462
]
3
20[e
.462
]
n1
,
1
2
3
2
1
2
1
1
2
SPECIAL TOPICS 12.3.A Infinite Series 855
