Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

SOLUTION
(a) Sin
1
(1/2) is the one number between p/2 and p/2 whose sine is 1/2.
From our study of special values, we know that sin p/6 1/2, and p/6 is
between p/2 and p/2. Hence, sin
1
(1/2) p/6.
(b) Sin
1
(2
/2) p/4 because sin(p/4) 2
/2 and p/4 is
between p/2 and p/2. ■
EXAMPLE 2
Except for special values (as in Example 1), you should use the SIN
1
key
(labeled ASIN on some calculators) in radian mode to evaluate the inverse sine
function. For instance,
sin
1
(.67) .7342 and sin
1
(.42) .4334. ■
EXAMPLE 3
If you key in SIN
1
2 ENTER, you will get an error message, because 2 is not in
the domain of the inverse sine function.* ■
Suppose 1 v 1 and sin
1
v u. Then by the definition of the inverse
sine function, we know that p/2 u p/2 and sin u v. Therefore,
sin
1
(sin u) sin
1
(v) u and sin(sin
1
v) sin u v.
This shows that the restricted sine function and the inverse sine function have the
usual “round-trip properties” of inverse functions. In summary,
546 CHAPTER 7 Trigonometric Identities and Equations
CAUTION
The notation sin
1
x is not exponential notation. It does not mean either (sin x)
1
or
si
1
n x
. For instance, Example 1 shows that
sin
1
(1/2) p/6 .5236,
but
sin
1
2
1
.47
1
94
2.0858.
1
sin
1
2
Properties of
Inverse Sine
sin
1
(sin u) u if
p
2
u
p
2
sin(sin
1
v) v if 1 v 1
*TI-85/86 and HP-39gs display the complex number (1.5707 , 1.3169 ) for sin
1
(2). For our
purposes, this is equivalent to an error message, since we deal only with functions whose values are
real numbers.
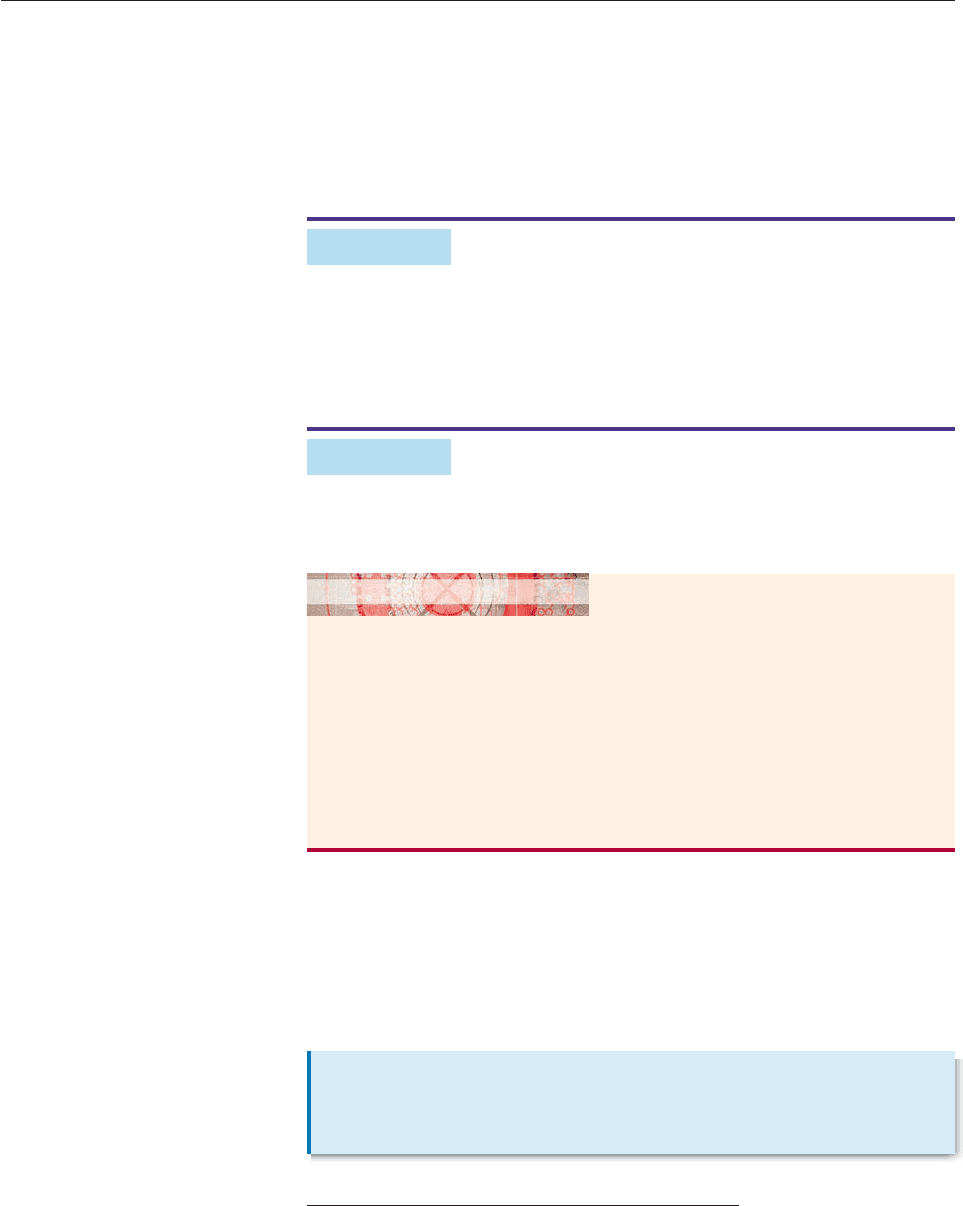
A calculator can illustrate the identities in the preceding box, as shown in Fig-
ure 7–12. Nevertheless, when special values are involved, you should be able to
deal with them by hand.
EXAMPLE 4
Find (a) sin
1
(sin p/6) (b) sin
1
(sin 5p/6).
SOLUTION
(a) We know that sin p/6 1/2. Hence,
sin
1
sin
p
6
sin
1
1
2
p
6
because p/6 is the number between p/2 and p/2 whose sine is 1/2.
(b) We also have sin 5p/6 1/2, so the expression sin
1
(sin 5p/6) is defined.
However,
sin
1
sin
5
6
p
is NOT equal to
5
6
p
because the identity in the box on page 546 is valid only when u is between
p/2 and p/2. Using the result of part (a), we see that
sin
1
sin
5
6
p
sin
1
1
2
p
6
. ■
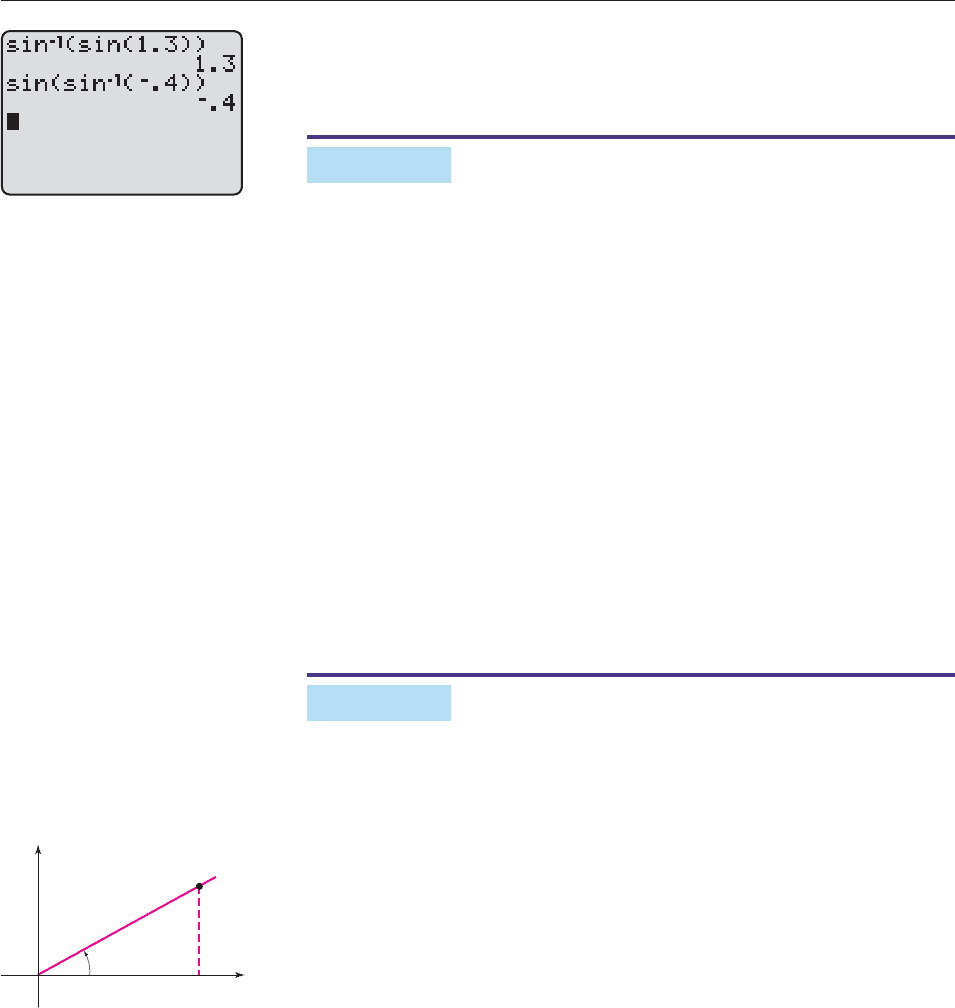
EXAMPLE 5
Find the exact value of tan
sin
1
5
9
.
SOLUTION Let sin
1
5
9
t. We must find tan t, so we construct an angle of
t radians in standard position (Figure 7–13). Let (x, y) be the point on the terminal
side of the angle that is 9 units from the origin. By the point-in-the plane descrip-
tion, we have
sin t
9
y
and tan t
y
x
.
Consequently,
9
y
sin t sin
sin
1
5
9
5
9
.
The first and last terms of this equation show that y 5. Applying the
Pythagorean Theorem to the right triangle in Figure 7–13, we see that
x
2
5
2
9
2
x
2
25 81
x
2
56
x 56.
SECTION 7.4 Inverse Trigonometric Functions 547
Figure 7–12
(x, y)
9
t
x
y
Figure 7–13
Therefore,
tan
sin
1
5
9
tan t
y
x
5
56
. ■
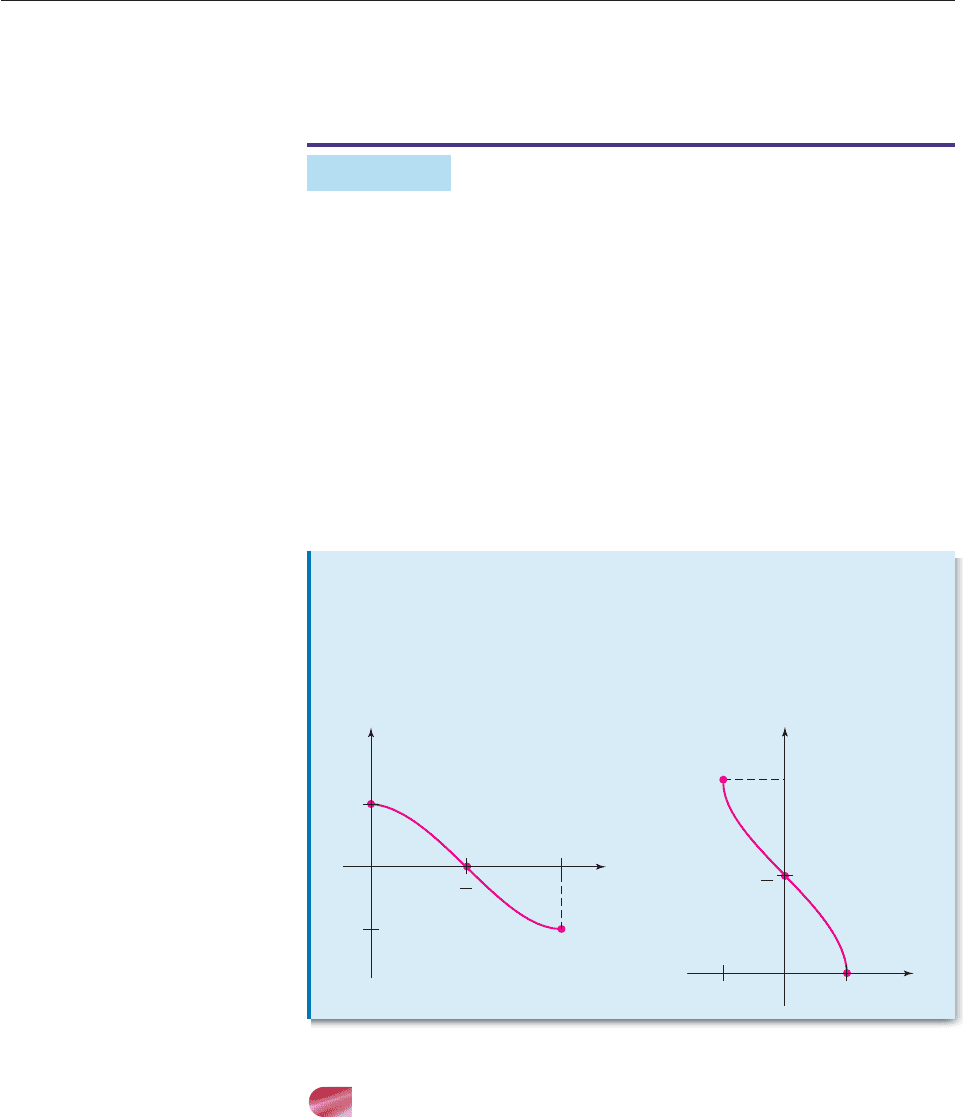
Recall that the graph of the inverse function of f can be obtained in two ways:
Reverse the coordinates of each point on the graph of f or, equivalently, reflect the
graph of f in the line y x, as explained on pages 224–225. In summary,
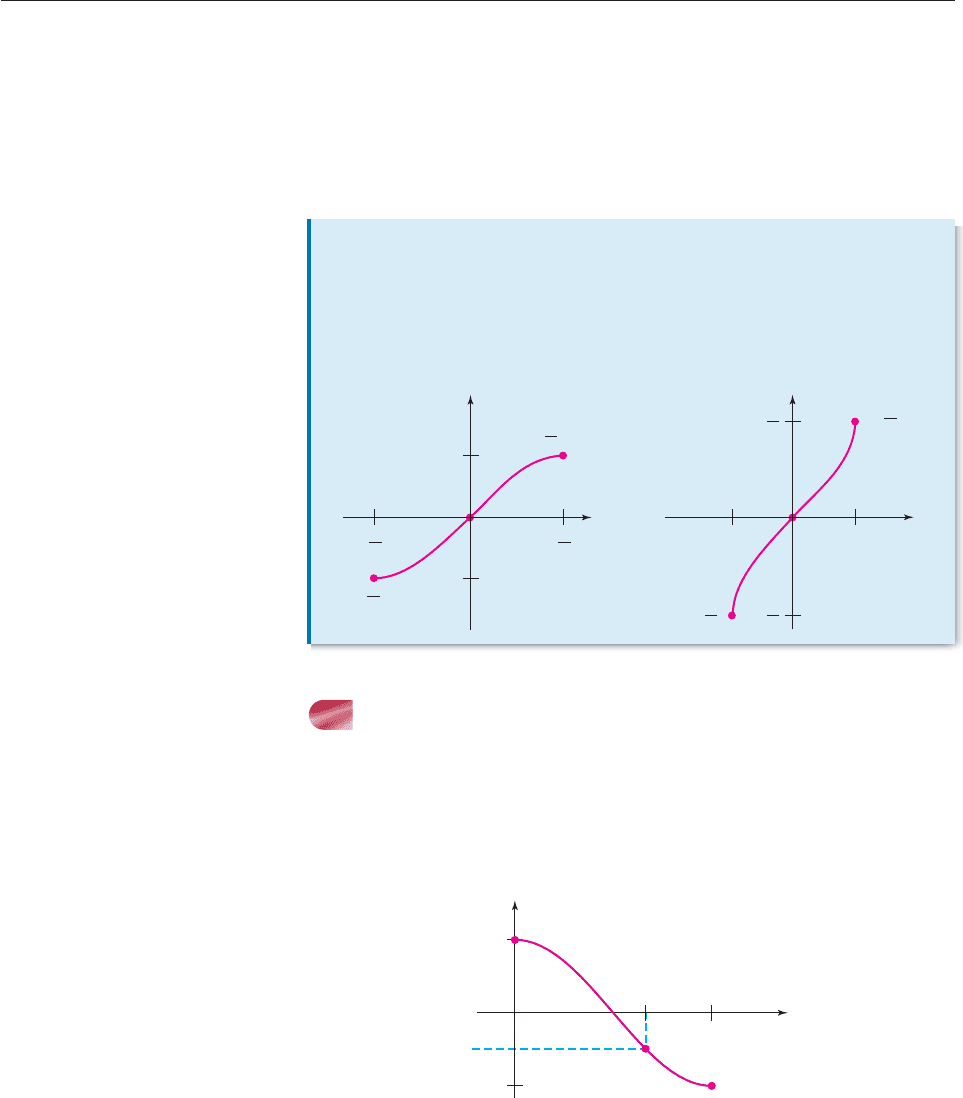
THE INVERSE COSINE FUNCTION
The restricted cosine function is defined as follows:
Domain: [0, p] Rule: f (x) cos x.
Its graph in Figure 7–14 shows that for each number v between 1 and 1, there is
exactly one number u between 0 and p such that cos u v.
Figure 7–14
Since the graph of the restricted cosine function passes the Horizontal Line
Test, we know that it has an inverse function. This inverse function is called the
inverse cosine (or arccosine) function and is denoted by h(x) cos
1
x or
h(x) arccos x. The domain of the inverse cosine function is the interval [1, 1],
and its rule is as follows.
x
y
v
u π
−1
1
(u, v) = (u, cos u)
548 CHAPTER 7 Trigonometric Identities and Equations
Restricted Sine Function Inverse Sine Function
f (x) sin xg(x) sin
1
x
Domain: [p/2, p/2] Domain: [1, 1]
Range: [1, 1] Range: [p/2, p/2]
1−1
2
π
2
π
2
π
1,
)
)
2
π
−1, −−
)
)
x
y
1
−1
2
π
2
π
2
π
, 1
)
)
2
π
, −1
−
−
)
)
x
y
EXAMPLE 6
Find (a) cos
1
(1/2) (b) cos
1
(0) (c) cos
1
(.63).
SOLUTION
(a) Cos
1
(1/2) p/3 since p/3 is the unique number between 0 and p whose
cosine is 1/2.
(b) Cos
1
(0) p/2 because cos p/2 0 and 0 p/2 p.
(c) The COS
1
key on a calculator in radian mode shows that
cos
1
(.63) 2.2523. ■
EXAMPLE 7
Write sin(cos
1
v) as an algebraic expression in v.
SOLUTION Cos
1
v u, where cos u v and 0 u p. Hence, sin u is non-
negative, and by the Pythagorean identity, sin u
sin
2
u
1 co
s
2
u
. Also,
cos
2
u v
2
. Therefore,
sin(cos
1
v) sin u
1 co
s
2
u
1 v
2
. ■
EXAMPLE 8
Prove the identity sin
1
x cos
1
x p/2.
SOLUTION Suppose sin
1
x u, with p/2 u p/2. Verify that
0 p/2 u p (Exercise 24). Then we have
sin u x [Definition of inverse sine]
cos
p
2
u
x [Cofunction identity]
cos
1
x
p
2
u. [Definition of inverse cosine]
SECTION 7.4 Inverse Trigonometric Functions 549
Inverse Cosine
Function
For each v with 1 v 1,
cos
1
v the unique number u between 0 and p whose cosine is v;
that is,
cos
1
v u exactly when cos u v.
The inverse cosine function has these properties:
cos
1
(cos u) u if 0 u p;
cos(cos
1
v) v if 1 v 1.
CAUTION
cos
1
x does not mean
(cos x)
1
, or 1/cos x.
Therefore,
sin
1
x cos
1
x u
p
2
u
p
2
. ■
EXAMPLE 9
Prove that
sin(cos
1
x) cos(sin
1
x).
SOLUTION By the identity in Example 8,
sin(cos
1
x) sin
p
2
sin
1
x
cos(sin
1
x) [Cofunction identity] ■
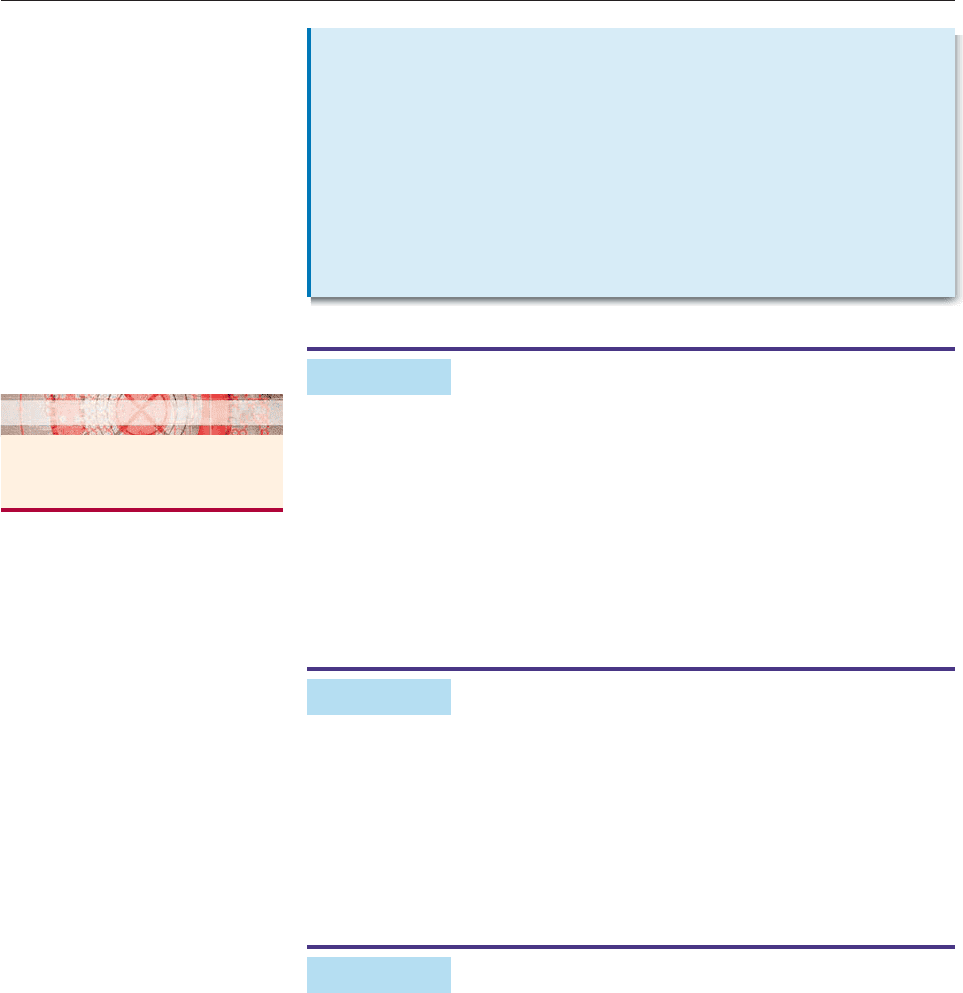
The graph of the inverse cosine function is the reflection of the graph of the
restricted cosine function in the line y x, as shown below.
THE INVERSE TANGENT FUNCTION
The restricted tangent function is defined as follows:
Domain: (p/2, p/2) Rule: f(x) tan x.
Its graph in Figure 7–15 shows that for every real number v, there is exactly one
number u between p/2 and p/2 such that tan u v.
550 CHAPTER 7 Trigonometric Identities and Equations
Restricted Cosine Function Inverse Cosine Function
f (x) cos xg(x) cos
1
x
Domain: [0, p] Domain: [1, 1]
Range: [1, 1] Range: [0, p]
2
π
(−1, π)
(1, 0)
0
−11
π
x
y
(0, 1)
(π, −1)
0
−1
1
2
ππ
x
y
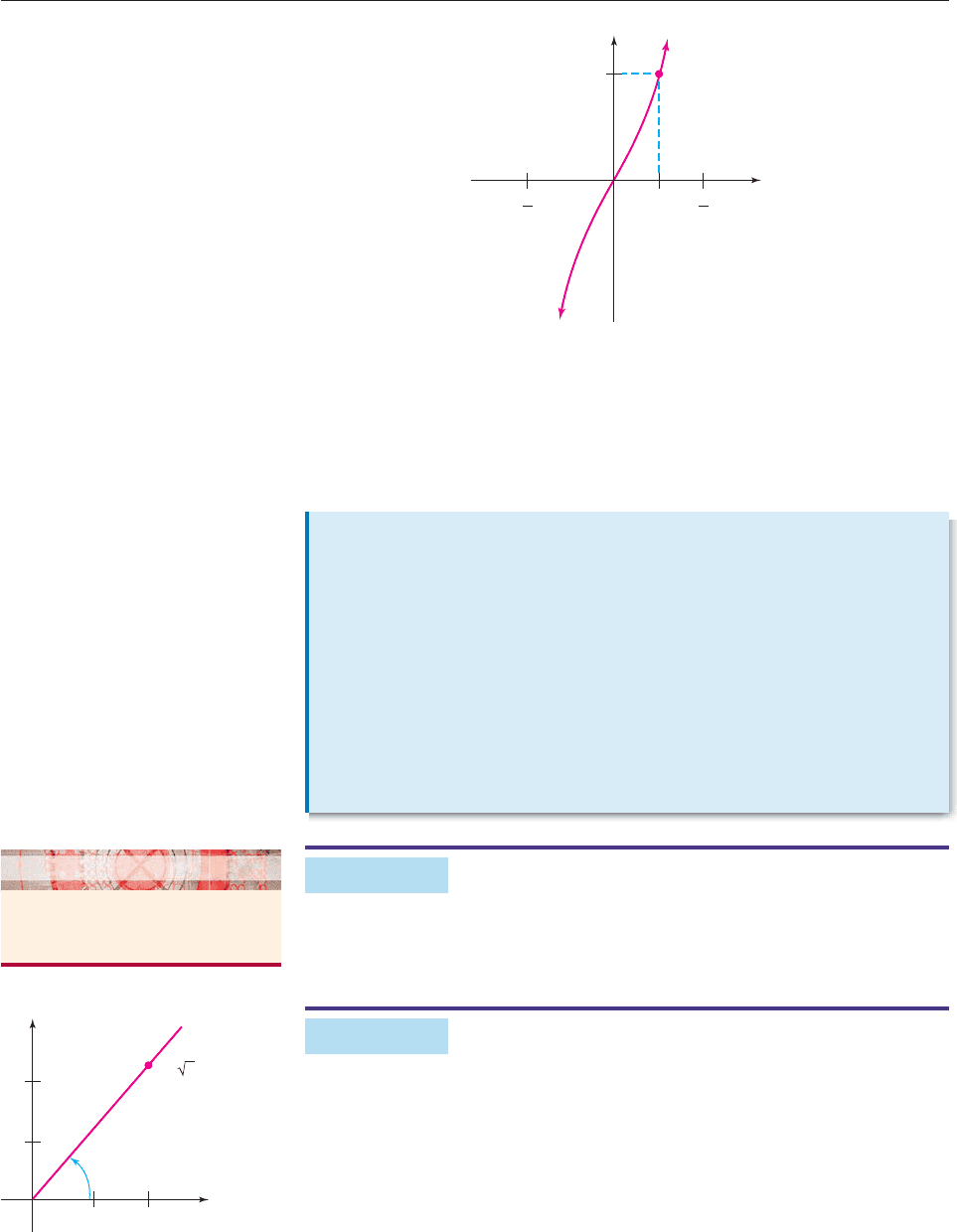
Figure 7–15
Since the graph of the restricted tangent function passes the horizontal line
test, we know that it has an inverse function. This inverse function is called the
inverse tangent (or arctangent) function and is denoted by g(x) tan
1
x or
g(x) arctan x. The domain of the inverse tangent function is the set of all real
numbers, and its rule is as follows.
EXAMPLE 10
Tan
1
1 p/4 because p/4 is the unique number between p/2 and p/2 such
that tan p/4 1. A calculator in radian mode shows that tan
1
(136) 1.5634.
■
EXAMPLE 11
Find the exact value of cos[tan
1
(5
/2)].
SOLUTION Consider an angle of u radians in standard position whose terminal
side passes through (2, 5
), as in Figure 7–16. By the point-in-the-plane description,
tan u 5
/2.
Since u is between p/2 and p/2 and tan u 5
/2, we must have
u tan
1
(5
/2).
π
2
(u, v) = (u, tan u)
v
−
x
u
y
π
2
SECTION 7.4 Inverse Trigonometric Functions 551
Inverse Tangent
Function
For each real number v,
tan
1
v the unique number u between p/2 and p/2 whose tangent is v;
that is,
tan
1
v u exactly when tan u v.
The inverse tangent function has these properties:
tan
1
(tan u) u if
p
2
u
p
2
;
tan(tan
1
v) v for every number v.
CAUTION
tan
1
x does not mean
(tan x)
1
, or 1/tan x.
u
2
2
x
y
(2, 5)
Figure 7–16

Furthermore, the distance from (2, 5
) to the origin is
(2 0
)
2
(
5
0)
2
4 5
3,
so
cos u 2/3.
Therefore,
cos[tan
1
(5
/2)] cos u 2/3. ■
The graph of the inverse tangent function is the reflection of the graph of the
restricted tangent function in the line y x, as shown below.
EXAMPLE 12
A 26-foot high movie screen is located 12 feet above the ground, as shown in
Figure 7–17. Assume that when you are seated your eye is 4 feet above the ground.
(a) Express the angle of t radians as a function of your distance x from the wall
holding the screen.
(b) How far should you be from the wall to make t as large as possible?
552 CHAPTER 7 Trigonometric Identities and Equations
Restricted Tangent Function Inverse Tangent Function
f (x) tan xg(x) tan
1
x
Domain: (p/2, p/2) Domain: All real numbers
Range: All real numbers Range: (p/2, p/2)
−1
0
2
π
2
π
4
π
1,
)
)
4
π
−1,
−
−
)
)
x
y
−1
1
−
0
2
π
2
π
4
π
, 1
)
)
4
π
, −1
−
)
)
x
y
26
12
4
x
t
Figure 7–17
t
u
(x, 8)
(x, 34)
x
y
Figure 7–18

SOLUTION
(a) Imagine that the x-axis is at your eye level with your eye at the origin. Since
your eye is 4 feet above the ground, the bottom of the screen is 8 feet above
your eye level and the situation looks like Figure 7–18. The point-in-the-
plane description shows that
tan u
8
x
and tan(u t)
3
x
4
.
Hence,
u tan
1
8
x
and u t tan
1
3
x
4
,
so that
t (u t) u tan
1
3
x
4
tan
1
8
x
.
(b) We graph the function t tan
1
3
x
4
tan
1
8
x
and use a maximum finder to
determine that t is largest when x 16.5 feet (Figure 7–19). ■
SECTION 7.4 Inverse Trigonometric Functions 553
Figure 7–19
1
020
EXERCISES 7.4
In Exercises 1–14, find the exact functional value without using
a calculator.
1. sin
1
1 2. cos
1
0 3. tan
1
(1)
4. sin
1
(1) 5. cos
1
1 6. tan
1
1
7. tan
1
(3
/3) 8. cos
1
(3
/2)
9. sin
1
(2
/2) 10. sin
1
(3
/2)
11. tan
1
(3
) 12. cos
1
(2
/2)
13. cos
1
1
2
14. sin
1
1
2
In Exercises 15–23, use a calculator in radian mode to approx-
imate the functional value.
15. sin
1
.35 16. cos
1
.76
17. tan
1
(3.256) 18. sin
1
(.795)
19. sin
1
(sin 7) [The answer is not 7.]
20. cos
1
(cos 3.5) 21. tan
1
[tan(4)]
22. sin
1
[sin(2)] 23. cos
1
[cos(8.5)]
24. Let u be a number such that
p
2
u
p
2
.
Prove that
0
p
2
u p.
25. Given that u sin
1
(3
/2), find the exact value of
cos u and tan u.
26. Given that u tan
1
(4/3), find the exact value of sin u and
sec u.
In Exercises 27–48, find the exact functional value without
using a calculator.
27. sin
1
(cos 0) 28. cos
1
(sin p/6)
29. cos
1
(sin 4p/3) 30. tan
1
(cos p)
31. sin
1
(cos 7p/6) 32. cos
1
(tan 7p/4)
33. sin
1
(sin 2p/3) (See Exercise 19.)
34. cos
1
(cos 5p/4) 35. cos
1
[cos(p/6)]
36. tan
1
[tan(4p/3)]
37. sin[cos
1
(3/5)] (See Example 11.)
38. tan[sin
1
(3/5)] 39. cos[tan
1
(3/4)]
40. cos[sin
1
(12/13)] 41. tan[cos
1
(5/13)]
42. sin[tan
1
(12/5)] 43. cos[sin
1
(3
/5)]
44. tan[sin
1
(7
/12)] 45. sin[cos
1
(3/13)]
46. tan[cos
1
(8/9)] 47. sin[tan
1
(5
/10)]
48. cos[tan
1
(3/7)]
In Exercises 49–55, write the expression as an algebraic
expression in v, as in Example 7.
49. cos(sin
1
v) 50. tan(cos
1
v)
51. tan(sin
1
v) 52. sin(tan
1
v)
53. cos(tan
1
v) 54. sin(2 sin
1
v)
55. sin(2 cos
1
v)
In Exercises 56–58, prove the identity.
56. tan(sin
1
v) cot(cos
1
v)
57. tan(cos
1
v) cot(sin
1
v)
58. sec(sin
1
v) csc(cos
1
v)
In Exercises 59–62, graph the function.
59. f (x) cos
1
(x 1) 60. g(x) tan
1
x p
61. h(x) sin
1
(sin x) 62. k(x) sin(sin
1
x)
63. In an alternating current circuit, the voltage is given by the
formula
V V
max
sin(2pft f),
where V
max
is the maximum voltage, f is the frequency (in
cycles per second), t is the time in seconds, and f is the
phase angle.
(a) If the phase angle is 0, solve the voltage equation for t.
(b) If f 0, V
max
20, V 8.5, and f 120, find the
smallest positive value of t.
64. Calculus can be used to show that the area A between the x-
axis and the graph of y
x
2
1
1
from x a to x b is
given by
A tan
1
b tan
1
a.
Find the area A when
(a) a 0 and b 1 (b) a 1 and b 2
(c) a 2.5 and b .5.
Note: Example 12 may be helpful for Exercises 65–71.
65. A model plane 40 feet above the ground is flying away from
an observer.
(a) Express the angle of elevation u of the plane as a func-
tion of the distance x from the observer to the plane.
(b) What is u when the plane is 250 feet away from the
observer?
66. Suppose that another model plane is flying while attached
to the ground by a 100 foot long wire that is always kept
taut. Let h denote the height of the plane above the ground
and u the radian measure of the angle the wire makes with
the ground. (The figure for Exercise 65 is the case when x
100 and h 40.)
(a) Express u as a function of the height h.
(b) What is u when the plane is 55 feet above the ground?
(c) When u 1 radian, how high is the plane?
x
Observer
40
θ
ba
y
x
2
1
1
y
x
67. A rocket is fired straight up. The line of sight from an ob-
server 4 miles away makes an angle of t radians with the
horizontal.
(a) Express t as a function of the height h of the rocket.
(b) Find t when the rocket is .25 mile, 1 mile, and 2 miles
high respectively.
(c) When t .4 radian, how high is the rocket?
68. A cable from the top of a 60-foot high tower is to be attached
to the ground x feet from the base of the tower.
(a) If the cable makes an angle of t radians with the ground
when attached, express t as a function of x. [Hint: Select
a coordinate system in which both x and t are positive,
or use Section 8.1.]
(b) What is t when the distance x 40 feet? When x
70 feet? When x 100 feet?
(c) If t p/5, how far is the end of the cable from the base
of the tower?
69. Suppose that the movie screen in Example 12 is 24 feet high
and is 10 feet above the ground and that the eye level of the
watcher is 4 feet above the ground.
(a) Express the angle t at the watcher’s eye as a function of
her distance x from the wall holding the screen.
(b) At what distance from the screen is the angle t as large
as possible?
70. Section 8.1 is a prerequisite for this exercise. A camera on a
5-foot-high tripod is placed in front of a 6-foot-high picture
that is mounted 3 feet above the floor.
x
6 ft
3 ft
5 ft
θ
x
t
60
h
t
4 mi
observer
554 CHAPTER 7 Trigonometric Identities and Equations

(a) Express angle u as a function of the distance x from the
camera to the wall.
(b) The photographer wants to use a particular lens, for
which u 36° (p/5 radians). How far should she place
the camera from the wall to be sure that the entire pic-
ture will show in the photograph?
71. A 15-foot-wide highway sign is placed 10 feet from a road,
perpendicular to the road (see figure). A spotlight at the
edge of the road is aimed at the sign.
(a) Express u as a function of the distance x from point A to
the spotlight.
(b) How far from point A should the spotlight be placed so
that the angle u is as large as possible?
72. Show that the restricted secant function, whose do-
main consists of all numbers x such that 0 x p and
x p/2, has an inverse function. Sketch its graph.
73. Show that the restricted cosecant function, whose domain
consists of all numbers x such that p/2 x p/2 and
x 0, has an inverse function. Sketch its graph.
74. Show that the restricted cotangent function, whose domain is
the interval (0, p), has an inverse function. Sketch its graph.
Sign
10
Spotlight
θ
A
75. Show that the inverse cosine function actually has the two
properties listed in the box on page 549.
76. Show that the inverse tangent function actually has the two
properties listed in the box on page 551.
In Exercises 77–84, prove the identity.
77. sin
1
(x) sin
1
x [Hint: Let u sin
1
(x) and show
that sin
1
x u.]
78. tan
1
(x) tan
1
x
79. cos
1
(x) p cos
1
x [Hint: Let u cos
1
(x) and
show that 0 p u p ; use the identity
cos(p u) cos u.]
80. sin
1
(cos x) p/2 x (0 x p)
81. tan
1
(cot x) p/2 x (0 x p)
82. tan
1
x tan
1
1
x
p
2
83. sin
1
x tan
1
(1 x 1)
[Hint: Let u sin
1
x and show that
tan u x/
1 x
2
. Since sin u x,
cos u
1 x
2
. Show that in this case,
cos u
1 x
2
.]
84. cos
1
x
p
2
tan
1
(1 x 1)
[Hint: See Example 8 and Exercise 83.]
85. Is it true that tan
1
x
c
s
o
in
s
1
1
x
x
? Justify your answer.
86. Using the viewing window with 2p x 2p and
4 y 4 graph the functions f(x) cos(cos
1
x) and
g(x) cos
1
(cos x). How do you explain the shapes of
the two graphs?
x
1 x
2
x
1 x
2
SECTION 7.5 Trigonometric Equations 555
7.5 Trigonometric Equations
■ Solve basic trigonometric equations.
■ Solve other trigonometric equations.
Any equation that involves trigonometric functions can be solved graphically, and
many can be solved algebraically. Unlike the equations solved previously,
trigonometric equations typically have an infinite number of solutions. In most
cases, these solutions can be systematically determined by using periodicity, as
we now see.
Section Objectives
