Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


EXAMPLE 1
If p x 3p/2 and cos x 8/17, find sin 2x and cos 2x, and show that
5p/2 2x 3p.
SOLUTION To use the double-angle identities, we first must determine sin x.
It can be found by using the Pythagorean identities.
sin
2
x 1 cos
2
x 1
1
8
7
2
1
2
6
8
4
9
2
2
2
8
5
9
.
Since p x 3p/2, we know sin x is negative. Therefore,
sin x
2
2
2
8
5
9
1
1
5
7
.
We now substitute these values in the double-angle identities.
sin 2x 2 sin x cos x 2
1
1
5
7
1
8
7
2
2
4
8
0
9
.83
cos 2x cos
2
x sin
2
x
1
8
7
2
1
1
5
7
2
2
6
8
4
9
2
2
2
8
5
9
1
2
6
8
1
9
.56.
Since p x 3p/2, we know that 2p 2x 3p. The calculations above show
that at 2x, sine is positive and cosine is negative. This can occur only if 2x lies
between 5p/2 and 3p. ■
EXAMPLE 2
Express the rule of the function f (x) sin 3x in terms of sin x and constants.
SOLUTION We first use the addition identity for sin(x y) with y 2x.
f (x) sin 3x sin(x 2x) sin x cos 2x cos x sin 2x.
Next apply the double-angle identities for cos 2x and sin 2x.
f (x) sin 3x sin x cos 2x cos x sin 2x
sin x(cos
2
x sin
2
x) cos x(2 sin x cos x)
sin x cos
2
x sin
3
x 2 sin x cos
2
x
3 sin x cos
2
x sin
3
x.
Finally, use the Pythagorean identity.
f (x) sin 3x 3 sin x cos
2
x sin
3
x 3 sin x(1 sin
2
x) sin
3
x
3 sin x 3 sin
3
x sin
3
x 3 sin x 4 sin
3
x. ■
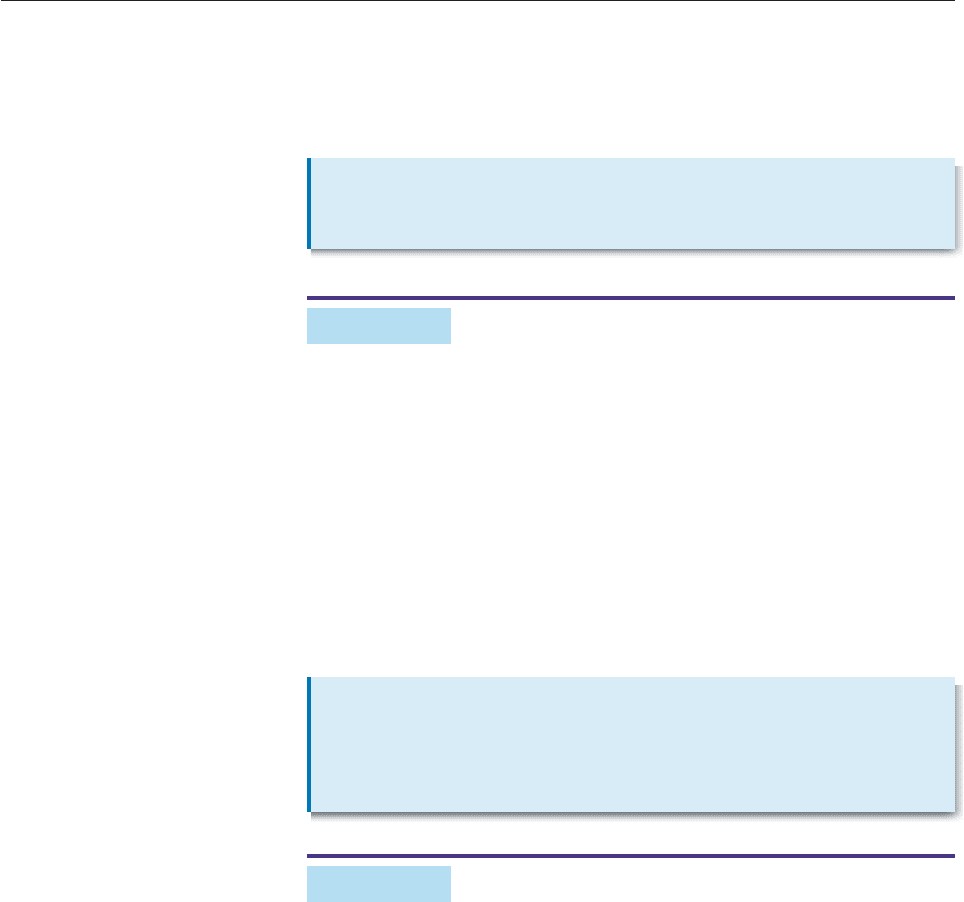
The double-angle identity for cos 2x can be rewritten in several useful ways.
For instance, we can use the Pythagorean identity in the form of cos
2
x 1 sin
2
x
to obtain:
cos 2x cos
2
x sin
2
x (1 sin
2
x) sin
2
x 1 2 sin
2
x.
536 CHAPTER 7 Trigonometric Identities and Equations
Similarly, using the Pythagorean identity in the form sin
2
x 1 cos
2
x, we have:
cos 2x cos
2
x sin
2
x cos
2
x (1 cos
2
x) 2 cos
2
x 1.
In summary:
EXAMPLE 3
Prove that
1
sin
co
2
s
x
2x
tan x.
SOLUTION The first identity in the preceding box and the double-angle iden-
tity for sine show that
1
sin
co
2
s
x
2x
1
2s
(1
in
x c
2
o
s
s
in
x
2
x)
2s
2
in
s
x
in
c
2
o
x
s x
c
s
o
in
s
x
x
tan x. ■
If we solve the first equation in the preceding box for sin
2
x and the second
one for cos
2
x, we obtain a useful alternate form for these identities.
EXAMPLE 4
Express the rule of the function f (x) sin
4
x in terms of constants and first pow-
ers of the cosine function.
SOLUTION We begin by applying the power-reducing identity.
f (x) sin
4
x sin
2
x sin
2
x
1 c
2
os 2x
1 c
2
os 2x
.
Next we apply the power-reducing identity for cosine to cos
2
2x. Note that this
means using 2x in place of x in the identity.
cos
2
2x
1 co
2
s 2(2x)
1 c
2
os 4x
.
1 2 cos 2x cos
2
2x
4
SECTION 7.3 Other Identities 537
More Double-Angle
Identities
cos 2x 1 2 sin
2
x
cos 2x 2 cos
2
x 1
Power-Reducing
Identities
sin
2
x
1 c
2
os 2x
cos
2
x
1 c
2
os 2x

Finally, we substitute this last result in the expression for sin
4
x above.
f (x) sin
4
x
1
4
1
2
cos 2x
1
8
(1 cos 4x)
3
8
1
2
cos 2x
1
8
cos 4x. ■
HALF-ANGLE IDENTITIES
If we use the power-reducing identity with x/2 in place of x, we obtain
sin
2
2
x
1
2
cos x
.
Consequently, we must have
sin
2
x
1
2
co
s x
.
This proves the first of the half-angle identities.
The half-angle identity for cosine is derived from a power-reducing identity, as
was the half-angle identity for sine. The half-angle identity for tangent then fol-
lows immediately since tan(x/2) sin(x/2)/cos(x/2). In all cases, the sign in
front of the radical depends on the quadrant in which x/2 lies.
EXAMPLE 5
Find the exact value of
(a) cos
5
8
p
(b) sin
1
p
2
.
SOLUTION
(a) Since
5
8
p
1
2
5
4
p
5p
2
/4
, we use the half-angle identity with x 5p/4
and the fact that cos(5p/4) 2
/2. The sign chart in Exercise 63 on
1 cos 2
2
x
2
1 2 cos 2x
1 c
2
os 4x
4
1 2 cos 2x cos
2
2x
4
538 CHAPTER 7 Trigonometric Identities and Equations
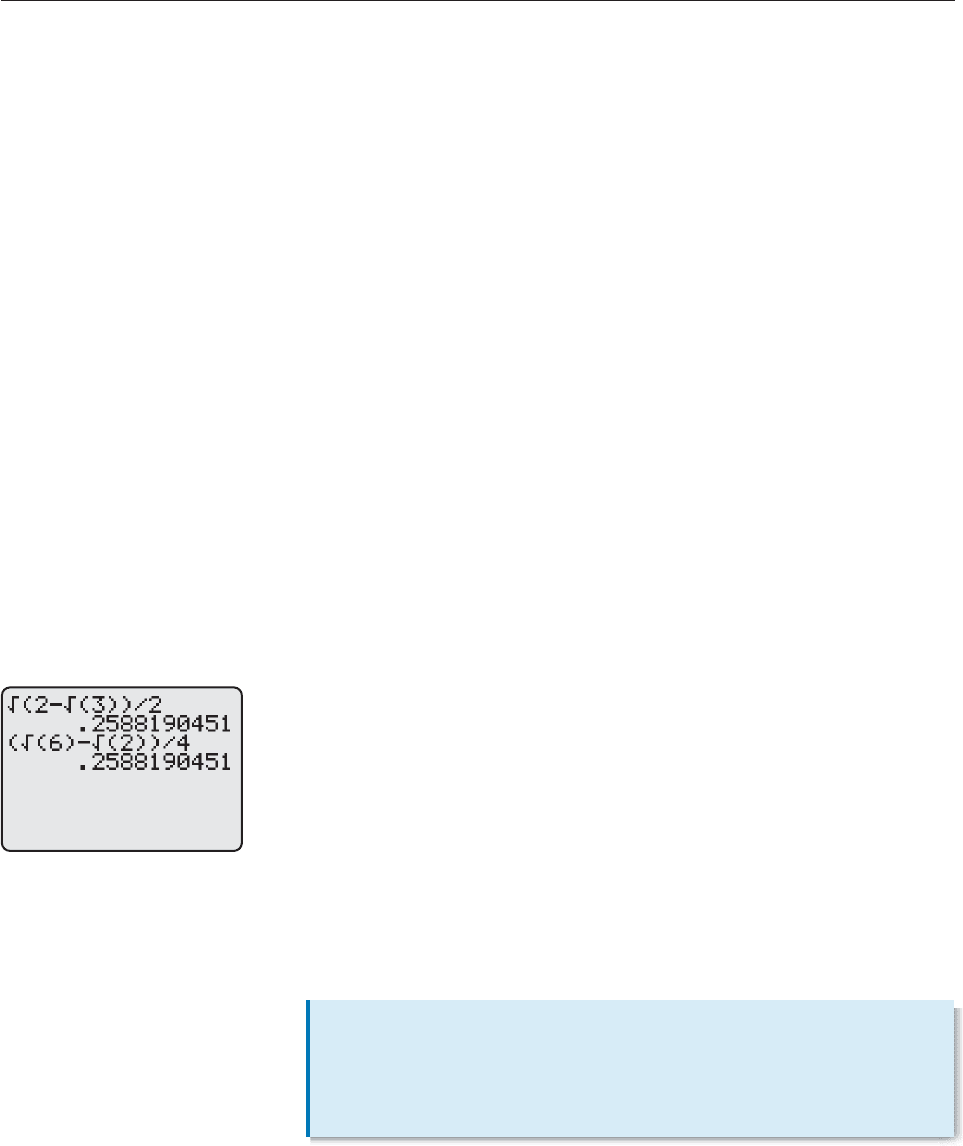
Half-Angle
Identities
sin
2
x
1
2
co
s x
cos
2
x
1
2
co
s x
tan
2
x
1
1
c
c
o
o
s
s
x
x
page 451 shows that cos(5p/8) is negative because 5p/8 is in the second
quadrant. So we use the negative sign in front of the radical.
cos
5
8
p
cos
5p
2
/4
1 co
2
s(5p/4
)
1 (
2
2
/2
)
(2
2
2
)/2
2
4
2
2
2
2
.
(b) Since
1
p
2
1
2
p
6
p
2
/6
and p/12 is in the first quadrant, where sine is
positive, we have
sin
1
p
2
sin
p
2
/6
1 co
2
s(p/6
)
1
2
3
/2
(2
2
3
)/2
2
4
3
2
2
3
■
Example 5(b) shows that
sin
1
p
2
2
2
3
.
On the other hand, in Example 1(a) of Section 7.2 we proved that
sin
1
p
2
6
4
2
.
So we can conclude that
2
2
3
6
4
2
,
a fact that can readily be confirmed by a calculator (Figure 7–9). The moral here
is that there may be several correct ways to express the exact value of a trigono-
metric function.
The problem of determining signs in the half-angle formulas can be elimi-
nated with tangent by using these identities.
Proof In the identity
tan x
1
sin
co
2
s
x
2x
,
SECTION 7.3 Other Identities 539
Half-Angle Identities
for Tangent
tan
2
x
1
sin
co
x
s x
tan
2
x
1
sin
co
x
s x
Figure 7–9
which was proved in Example 3, replace x by x/2.
tan
2
x
1
sin
co
2
s
(x
2
/
(x
2
/
)
2)
1
sin
co
x
s x
.
The second identity in the box is proved in Exercise 89. ■
EXAMPLE 6
If tan x
3
2
and p x
3
2
p
, find tan
2
x
.
SOLUTION The terminal side of an angle of x radians in standard position lies
in the third quadrant, as shown in Figure 7–10. The tangent of the angle in stan-
dard position whose terminal side passes through the point (2, 3) is
3
2
3
2
.
Since there is only one angle in the third quadrant with tangent 3/2, the point
(2, 3) must lie on the terminal side of the angle of x radians.
Since the distance from (2, 3) to the origin is
(2
0)
2
(3
0)
2
13,
we have
sin x
1
3
3
and cos x
1
2
3
.
Therefore, by the first of the half-angle identities for tangent
tan
2
x
1
sin
co
x
s x
13
3
2
. ■
SUM/PRODUCT IDENTITIES
The following identities were proved in Example 5 and Exercises 60–62 of
Section 7.2.
13
1
3
2
1
3
3
1
1
2
3
1
3
3
540 CHAPTER 7 Trigonometric Identities and Equations
−2
−3
(−2, −3)
13
1
−1
x
x
y
Figure 7–10
Product to Sum
Identities
sin x cos y
1
2
[sin(x y) sin(x y)]
sin x sin y
1
2
[cos(x y) cos(x y)]
cos x cos y
1
2
[cos(x y) cos(x y)]
cos x sin y
1
2
[sin(x y) sin(x y)]

EXAMPLE 7
Express sin(3x) cos(5x) as a sum or difference of trigonometric functions.
SOLUTION We use the first product to sum identity, with 3x in place of x and
5x in place of y.
sin(3x) cos(5x)
1
2
[sin(3x 5x) sin(3x 5x)]
1
2
[sin(8x) sin(2x)]
1
2
[sin(8x) sin(2x)] [Negative angle identity]
1
2
sin(8x)
1
2
sin(2x) ■
If we use the first product to sum identity with
1
2
(x y) in place of x and
1
2
(x y) in place of y, we obtain
sin
1
2
(x y)
cos
1
2
(x y)
1
2
sin
1
2
(x y)
1
2
(x y)
sin
1
2
(x y)
1
2
(x y)
1
2
(sin x sin y).
Multiplying both sides of the last equation by 2 produces the first of the following
identities.
SECTION 7.3 Other Identities 541
The last three sum to product identities are proved in the same way as the first.
(See Exercises 59–61.)
EXAMPLE 8
Express cos(7x) cos(3x) as a product of trigonometric functions.
SOLUTION We use the third sum to product identity with 7x in place of x and
3x in place of y.
cos(7x) cos(3x) 2 cos
7x
2
3x
cos
7x
2
3x
2 cos
1
2
0x
cos
4
2
x
2 cos(5x)cos(2x) ■
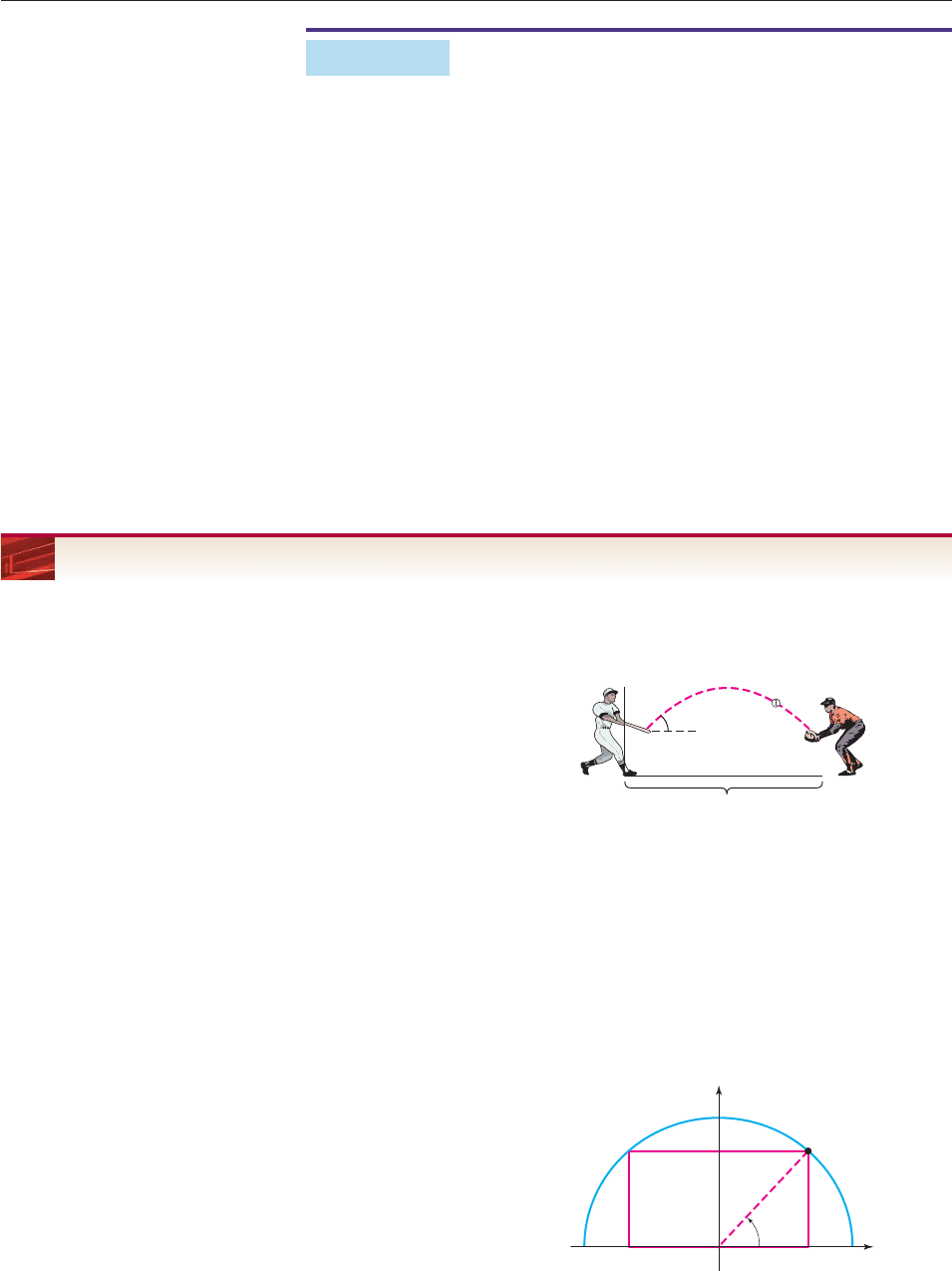
Sum to Product
Identities
sin x sin y 2 sin
x
2
y
cos
x
2
y
sin x sin y 2 cos
x
2
y
sin
x
2
y
cos x cos y 2 cos
x
2
y
cos
x
2
y
cos x cos y 2 sin
x
2
y
sin
x
2
y
EXAMPLE 9
Prove the identity
c
s
o
in
s
t
t
s
c
i
o
n
s
3
3
t
t
tan 2t.
SOLUTION Using the first factoring identity with x t and y 3t yields
sin t sin 3t 2 sin
t
2
3t
cos
t
2
3t
2 sin 2t cos(t).
Similarly,
cos t cos 3t 2 cos
t
2
3t
cos
t
2
3t
2 cos 2t cos(t),
so
c
s
o
in
s
t
t
s
c
i
o
n
s
3
3
t
t
2
2
c
s
o
in
s
2
2
t
t
c
c
o
o
s
s
(
(
t
t
)
)
c
s
o
in
s
2
2
t
t
tan 2t. ■
542 CHAPTER 7 Trigonometric Identities and Equations
EXERCISES 7.3
In Exercises 1–7, find sin 2x, cos 2x, and tan 2x under the given
conditions.
1. sin x
1
5
3
0 x
p
2
2. sin x
4
5
p x
3
2
p
3. cos x
3
5
p x
3
2
p
4. cos x
1
3
p
2
x p
5. tan x
3
4
p x
3
2
p
6. tan x
3
2
p
2
x p
7. csc x 4
0 x
p
2
8. A batter hits a baseball that is caught by a fielder. If the ball
leaves the bat at an angle of u radians to the horizontal, with
an initial velocity of v feet per second, then the approximate
horizontal distance d traveled by the ball is given by
d
v
2
sin
1
u
6
cos u
.
(a) Use an identity to show that
d
v
2
s
3
in
2
2u
.
(b) If the initial velocity is 115 ft/second, what angle u will
produce the maximum distance? [Hint: Use part (a).
For what value of u is sin 2u as large as possible?]
9. A rectangle is inscribed in a semicircle of radius 3 inches
and the radius to the corner makes an angle of t radians with
the horizontal, as shown in the figure.
(a) Express the horizontal length, vertical height, and area
of the rectangle in terms of x and y.
(b) Express x and y in terms of sine and cosine.
(c) Use parts (a) and (b) and suitable identities to show that
the area A of the rectangle is given by
A 9 sin 2t.
(x, y)
y
x
t
d
θ

10. In Exercise 9, what angle will produce a rectangle with
largest possible area? What is this maximum area?
In Exercises 11–26, use the half-angle identities to evaluate the
given expression exactly.
11. cos
p
8
12. tan
p
8
13. sin
3
8
p
14. cos
3
8
p
15. tan
1
p
2
16. sin
5
8
p
17. cos
1
p
2
18. tan
5
8
p
19. sin
7
8
p
20. cos
7
8
p
21. tan
7
8
p
22. cot
p
8
23. cos
1
p
6
[Hint: Exercise 11] 24. sin
1
p
6
25. sin
2
p
4
[Hint: Exercise 17] 26. cos
2
p
4
In Exercises 27–32, find sin
2
x
, cos
2
x
, and tan
2
x
under the
given conditions.
27. cos x .4
0 x
p
2
28. sin x .6
p
2
x p
29. sin x
3
5
3
2
p
x 2p
30. cos x .8
3
2
p
x 2p
31. tan x
1
2
p x
3
2
p
32. cot x 1
p x
p
2
In Exercises 33–38, write each expression as a sum or
difference.
33. sin 4x cos 6x 34. sin 5x sin 7x
35. cos 2x cos 4x 36. sin 3x cos 5x
37. sin 17x sin(3x) 38. cos 13x cos(5x)
In Exercises 39–44, write each expression as a product.
39. sin 3x sin 5x 40. cos 2x cos 6x
41. sin 9x sin 5x 42. cos 5x cos 7x
43. cos 2x cos 5x 44. sin 4x sin 3x
In Exercises 45–50, assume sin x .6 and 0 x p/2 and
evaluate the given expression.
45. sin 2x 46. cos 4x 47. cos 2x 48. sin 4x
49. sin
2
x
50. cos
2
x
51. Express cos 3x in terms of cos x.
SECTION 7.3 Other Identities 543
52. (a) Express the rule of the function f (x) cos
3
x in terms of
constants and first powers of the cosine function as in
Example 4.
(b) Do the same for f(x) cos
4
x.
In Exercises 53–58, simplify the given expression.
53.
2
si
s
n
in
2x
x
54. 1 2 sin
2
2
x
55. 2 cos 2y sin 2y (Think!)
56. cos
2
2
x
sin
2
2
x
57. (sin x cos x)
2
sin 2x
58. 2 sin x cos
3
x 2 sin
3
x cos x
In Exercises 59–61, prove the given sum to product identity.
[Hint: See the proof on page 541.]
59. sin x sin y 2 cos
x
2
y
sin
x
2
y
60. cos x cos y 2 cos
x
2
y
cos
x
2
y
61. cos x cos y 2 sin
x
2
y
sin
x
2
y
62. When you press a key on a touch-tone phone, the key emits
two tones that combine to produce the sound wave
f(t) sin(2pLt) sin(2pHt),
Where t is in seconds, L is the low frequency tone for the
row the key is in, and H is the high frequency tone for the
column the key is in, as shown in the diagram below. For
example, pressing 2 produces the sound wave f (t)
sin [2p (697)t] sin [2p(1336)t].
(a) Write the function that gives the sound wave produced
by pressing the 6 key.
(b) Express the 6 key function in part (a) as the product of
a sine and a cosine function.
In Exercises 63–76, determine graphically whether the equa-
tion could possibly be an identity. If it could, prove that it is.
63. sin 16x 2 sin 8x cos 8x 64. cos 8x cos
2
4x sin
2
4x
65. cos
4
x sin
4
x cos 2x 66. sec 2x
1 2
1
sin
2
x
123
4
5
6
7
8
9
*0
#
697 Hz
1209 1336 1477 Hz
High frequency
Low
frequency
770 Hz
852 Hz
941 Hz
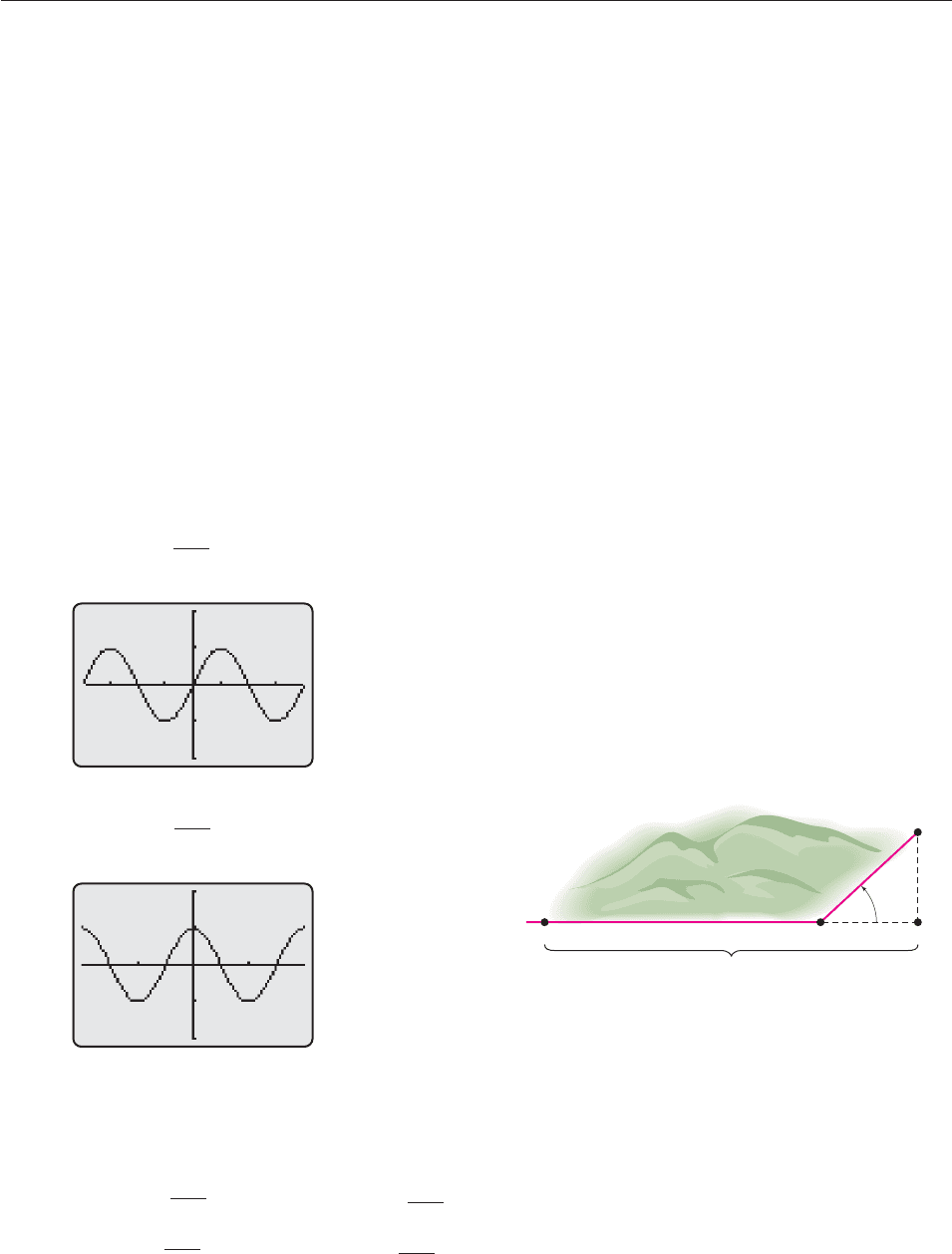
67. cos 4x 2 cos 2x 1 68. sin
2
x cos
2
x 2 sin x
69.
1
sin
co
2
s
x
2x
cot x 70. sin 2x
2
cs
c
c
o
2
t
x
x
71. sin 3x (sin x)(3 4 sin
2
x)
72. sin 4x (4 cos x sin x)(1 2 sin
2
x)
73. cos 2x
2
se
ta
c
n
2
x
x
74. cos 3x (cos x)(3 4 cos
2
x)
75. csc
2
2
x
1
2
cos x
76. sec
2
2
x
1
2
cos x
In Exercises 77 and 78, the graph of the left side of the expres-
sion is shown. Fill the blank on the right side with a simple
trigonometric expression and prove that the resulting equation
is an identity. [Hint: What trigonometric function has a graph
that closely resembles the given one?]
77.
sin
2
5x
co
s
s
4
i
x
n3x
78.
sin 5
2
x
s
in 4
si
x
n3x
In Exercises 79–82, fill the blank on the right side with a sim-
ple trigonometric expression and prove that the resulting equa-
tion is an identity. [Hint: Exercises 77 and 78.]
79.
cos
2
x
c
os
c
2
o
x
s3x
80.
c
s
o
in
s
4
4
x
x
c
si
o
n
s
6
6
x
x
81.
c
s
o
in
s x
3x
co
si
s
n
3
x
x
82.
c
s
o
in
s
x
x
c
si
o
n
s
3
3
x
x
2
2
2 2
2
2
2 2
544 CHAPTER 7 Trigonometric Identities and Equations
In Exercises 83–88, prove the identity.
83.
c
s
o
in
s
x
x
s
c
i
o
n
s
3
3
x
x
tan x 84.
c
s
o
in
s
x
x
s
c
i
o
n
s
3
3
x
x
cot 2x
85.
c
s
o
in
s
4
4
x
x
s
c
i
o
n
s
6
6
x
x
cot x
86.
c
c
o
o
s
s
8
8
x
x
c
c
o
o
s
s
4
4
x
x
cot 6x cot 2x
87.
c
s
o
in
s
x
x
s
c
i
o
n
s
y
y
cot
x
2
y
88.
c
s
o
in
s
x
x
s
c
i
o
n
s
y
y
tan
x
2
y
89. (a) Prove that
1
sin
co
x
s x
1
sin
co
x
s x
.
(b) Use part (a) and the half-angle identity proved in the
text to prove that
tan
2
x
1
sin
co
x
s x
.
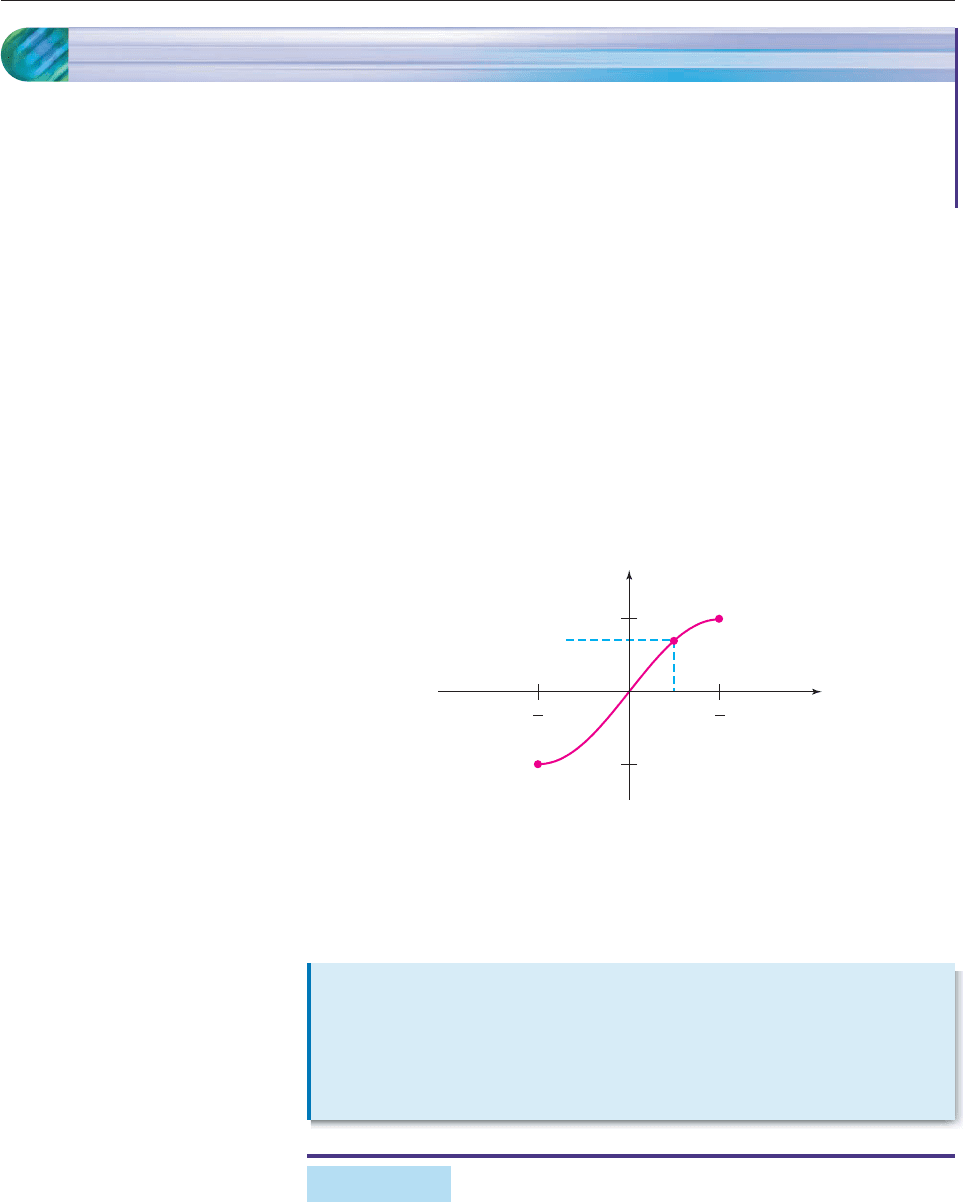
90. To avoid a steep hill, a road is being built in straight seg-
ments from P to Q and from Q to R; it makes a turn of t
radians at Q, as shown in the figure. The distance from P to
S is 40 miles, and the distance from R to S is 10 miles. Use
suitable trigonometric functions to express:
(a) c in terms of b and t [Hint: Place the figure on a coordi-
nate plane with P and Q on the x-axis, with Q at the
origin. Then what are the coordinates of R?]
(b) b in terms of t
(c) a in terms of t [Hint: a 40 c; use parts (a) and (b).]
(d) Use parts (b) and (c) and a suitable identity to show that
the length a b of the road is
40 10 tan
2
t
.
91. Find the exact value of cos
3
p
2
. [Hint: Exercise 23.]
92. (a) List the exact values of cos
p
4
, cos
p
8
, cos
1
p
6
, and
cos
3
p
2
. [Hint: Exercises 11, 23 and 91.]
(b) Based on the pattern you see in the answers to part
(a) make a conjecture about the exact value of cos
6
p
4
.
Use a calculator to support your answer.
(c) Make a conjecture about the exact value of cos
1
p
28
and
support the truth of your conjecture with a calculator.
(d) What do you think the exact value of cos
2
p
56
is?
t
R
S
40
10
QP
ac
b
SECTION 7.4 Inverse Trigonometric Functions 545
7.4 Inverse Trigonometric Functions
Section Objectives
■ Evaluate the inverse sine, cosine, and tangent functions.
■ Investigate the properties of the inverse trigonometric functions.
■ Prove identities involving inverse trigonometric functions.
■ Use inverse trigonometric functions to to solve applied problems.
Before reading this section, you should review the concept of an inverse function
(Section 3.7). As explained there, a function f has an inverse function only when
its graph passes the Horizontal Line Test:
No horizontal line intersects the graph of f more than once.
The graphs of the sine, cosine, and tangent functions certainly do not have this
property. However, functions that are closely related to them (same rules but
smaller domains) do have inverse functions.
The restricted sine function is defined as follows:
Domain: [p/2, p/2] Rule: f (x) sin x.
Its graph in Figure 7–11 shows that for each number v between 1 and 1, there is
exactly one number u between p/2 and p/2 such that sin u v.
Figure 7–11
Since the graph of the restricted sine function passes the horizontal line test, we
know that it has an inverse function. This inverse function is called the inverse sine
(or arcsine) function and is denoted by g(x) sin
1
x or g(x) arcsin x. The domain
of the inverse sine function is the interval [1, 1], and its rule is as follows.
EXAMPLE 1
Find
(a) sin
1
(1/2) (b) sin
1
(2
/2).
x
y
v
u
π
−1
−
1
(u, v) = (u, sin u)
2
π
2
Inverse Sine
Function
For each v with 1 v 1,
sin
1
v the unique number u between p/2 and p/2 whose sine is v;
that is,
sin
1
v u exactly when sin u v.
