Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


101. The number of hours of daylight in Detroit on day t of a
non–leap year (with t 0 being January 1) is given by the
function
d(t) 3 sin
3
2
6
p
5
(t 80)
12.
(a) On what days of the year are there exactly 11 hours of
daylight?
(b) What day has the maximum amount of daylight?
102. A weight hanging from a spring is set into motion (see Fig-
ure 6–69 on page 484), moving up and down. Its distance
(in centimeters) above or below the equilibrium point at
time t seconds is given by
d 5(sin 6t 4 cos 6t).
At what times during the first 2 seconds is the weight at the
equilibrium position (d 0)?
In Exercises 103–106, use the following fact: When a projectile
(such as a ball or a bullet) leaves its starting point at angle of
elevation u with velocity v, the horizontal distance d it travels is
given by the equation
d
3
v
2
2
sin 2u,
where d is measured in feet and v in feet per second. Note that
the horizontal distance traveled may be the same for two
different angles of elevation, so some of these exercises may
have more than one correct answer.
103. If muzzle velocity of a rifle is 300 feet per second, at what
angle of elevation (in radians) should it be aimed for the
bullet to hit a target 2500 feet away?
104. Is it possible for the rifle in Exercise 103 to hit a target that
is 3000 feet away? [At what angle of elevation would it
have to be aimed?]
105. A fly ball leaves the bat at a velocity of 98 mph and is
caught by an outfielder 288 feet away. At what angle of
elevation (in degrees) did the ball leave that bat?
d
(a)
θ
d
(b)
106. An outfielder throws the ball at a speed of 75 mph to the
catcher who is 200 feet away. At what angle of elevation
was the ball thrown?
THINKERS
107. Under what conditions (on the constant) does a basic equa-
tion involving the sine and cosine function have no
solutions?
108. Prove the formula L 2r sin
2
t
used in Exercises 53–60 as
follows.
(a) Construct the perpendicular line from the center of the
circle to the chord PQ, as shown in the figure. Verify
that triangles OCP and OCQ are congruent. [Hint:
Angles P and Q are equal by the Isosceles Triangle
Theorem,* and in each triangle, angle C is a right angle
(why?). Use the Congruent Triangles Theorem.*]
(b) Use part (a) to explain why angle POC measures t/2
radians.
(c) Show that the length of PC is r sin
2
t
.
(d) Use the fact that PC and QC have the same length to
conclude that the length L of PC is
L 2r sin
2
t
.
109. What is wrong with this so-called solution?
sin x tan x sin x
tan x 1
x
p
4
or
5
4
p
.
[Hint: Solve the original equation by moving all terms to
one side and factoring. Compare your answers with the
ones above.]
110. Let n be a fixed positive integer. Describe all solutions of
the equation sin nx 1/2. [Hint: See Exercises 43–52.]
P
Q
t
r
r
O
C
566 CHAPTER 7 Trigonometric Identities and Equations
*See the Geometry Review Appendix.

CHAPTER 7 Review 567
Chapter 7 Review
IMPORTANT CONCEPTS
Section 7.1
Reciprocal identities 516
Periodicity identities 516
Pythagorean identities 516
Negative angle identities 516
Strategies and proof techniques
for identities 516–521
Section 7.2
Addition and subtraction identities
524, 526
Cofunction identities 527
Special Topics 7.2.A
Angle of inclination 532
Angle between two lines 533
Slope theorem for perpendicular
lines 534
Section 7.3
Double-angle identities 535, 537
Power-reducing identities 537
Half-angle identities 538–539
Product to sum identities 540
Sum to product identities 541
Section 7.4
Inverse sine function 545–546
Inverse cosine function 548–549
Inverse tangent function 551
Section 7.5
Solution algorithms for basic
trigonometric equations 557–559
Algebraic solution of trigonometric
equations 560–562
Graphical solution of trigonometric
equations 562–563
IMPORTANT FACTS & FORMULAS
■ All identities in the Chapter 6 Review
■ Addition and Subtraction Identities:
sin(x y) sin x cos y cos x sin y
sin(x y) sin x cos y cos x sin y
cos(x y) cos x cos y sin x sin y
cos(x y) cos x cos y sin x sin y
tan(x y)
1
ta
n
t
x
a
n x
ta
ta
n
n
y
y
tan(x y)
1
ta
n
t
x
a
n x
ta
ta
n
n
y
y
■ Cofunction Identities:
sin x cos
p
2
x
cos x sin
p
2
x
tan x cot
p
2
x
cot x tan
p
2
x
sec x csc
p
2
x
csc x sec
p
2
x
■ Double-Angle Identities:
sin 2x 2 sin x cos x
cos 2x cos
2
x sin
2
x
cos 2x 2 cos
2
x 1 cos 2x 1 2 sin
2
x
tan 2x
1
2
ta
t
n
an
x
2
x

568 CHAPTER 7 Trigonometric Identities and Equations
■ Half-Angle Identities:
sin
2
x
1
2
co
s x
cos
2
x
1
2
co
s x
tan
2
x
1
sin
co
x
s x
tan
2
x
1
sin
co
x
s x
tan
2
x
1
1
c
c
o
o
s
s
x
x
■ sin
1
v u exactly when sin u v
p
2
u
p
2
, 1 v 1
■ cos
1
v u exactly when cos u v (0 u p, 1 v 1)
■ tan
1
v u exactly when tan u v
p
2
u
p
2
, any v
In Questions 1–4, simplify the given expression.
1.
2.
s
c
e
s
c
c
2
2
t
t
c
se
sc
c
t
t
3.
tan
2
x
se
c
2
x
sin
2
x
4.
In Questions 5–12, determine graphically whether the equation
could possibly be an identity. If it could, prove that it is.
5. sin
4
t cos
4
t 2 sin
2
t 1
6. 1 2 cos
2
t cos
4
t sin
4
t
7.
1
sin
co
t
s t
1
sin
co
t
s t
8.
c
s
o
in
s
2
2
t
t
1
co
1
s
2
t
9.
c
s
o
in
s
2
2
(
(
p
p
t
t
)
)
1
si
1
n
2
t
10. tan x cot x sec x csc x
11. (sin x cos x)
2
sin 2x 1
12.
1
ta
c
n
o
x
s2x
sin 2x
In Questions 13–22, prove the given identity.
13.
tan
2
x
t
an
s
x
in x
sin
2
2
x
14. 2 cos x 2 cos
3
x sin x sin 2x
15. cos(x y)cos(x y) cos
2
x sin
2
y
16.
c
c
o
o
s
s(
x
x
c
os
y
y
)
1 tan x tan y
(sin x cos x)(sin x cos x) 1
sin
2
x
sin
2
t (tan
2
t 2 tan t 4) cos
2
t
3 tan
2
t 3 tan t
17.
sec
ta
x
n
x
1
sec
ta
x
n
x
1
18.
co
1
s
4
x
tan
s
4
in
x
4
x
cos
4
x
19.
1
tan
ta
2
x
n
2
x
csc
2
x
20. sec x cos x sin x tan x
21. tan
2
x sec
2
x cot
2
x csc
2
x
22. sin 2x
tan x
1
cot 2x
23. If tan x 5/12 and sin x 0, find sin 2x.
24. If cos x 15/17 and 0 x p/2, find sin(x/2).
25. If tan x 4/3 with p x 3p/2, and cot y 5/12 with
3p/2 y 2p, find sin(x y).
26. If sin x 12/13 with p x 3p/2, and sec y 13/12
with 3p/2 y 2p, find cos(x y).
27. If sin x 1/4 and 0 x p/2, then sin(p/3 x) ?
28. If sin x 2/5 and 3p/2 x 2p, then cos(p/4 x) ?
29. If sin x 0, is it true that sin 2x 0? Justify your answer.
30. If cos x 0, is it true that cos 2x 0? Justify your answer.
31. Show that
2
3
2
2
6
by computing cos(p/12) in two ways, using the half-angle
identity and the subtraction identity for cosine.
32. True or false: 2 sin x sin 2x. Justify your answer.
33. Compute sin(5p/12) exactly.
34. Express sec(x p) in terms of sin x and cos x.
REVIEW QUESTIONS

CHAPTER 7 Test 569
35.
1
1
c
s
o
i
n
s
2
2
x
x
.
(a) tan x (b) cot x
(c)
1
1
c
s
o
i
n
s
2
2
x
x
(d) sec x
(e) undefined
36.
(csc x)
1
(sec
2
x)
.
(a)
(sin x)
1
(cos
2
x)
(b) sin x sin
3
x
(c)
(sin x)(1
1
tan
2
x)
(d) sin x
1
1
tan
2
x
(e) 1 tan
3
x
37. If sin x .6 and 0 x p/2, find sin 2x.
38. If sin x .6 and 0 x p/2, find sin(x/2).
39. If 1.9 and v
p
3
, find u.
40. A coil of wire rotating in a magnetic field induces voltage k,
where
k 15 sin
p
4
t
p
2
.
Use an appropriate identity to express k in terms of cos
p
4
t
.
41. Find the angle of inclination of the straight line through the
points (2, 6) and (2, 2).
42. Find one of the angles between the line L through the points
(3, 2) and (5, 1) and the line M, which has slope 2.
In Questions 43–52, exact answers are required.
43. cos
1
(2
/2) ? 44. cos
1
(3
/2) ?
45. tan
1
3
/3 ? 46. sin
1
(cos 11p/6) ?
47. cos
1
(sin 5p/3) ? 48. tan
1
(cos 7p/2) ?
49. sin
1
(sin .75) ? 50. cos
1
(cos 2) ?
51. sin
1
(sin 8p/3) ? 52. cos
1
(cos 13p/4) ?
53. Sketch the graph of f(x) tan
1
x p.
54. Sketch the graph of g(x) sin
1
(x 2).
cos
u
2
2
v
cos
u
2
55. Find the exact value of sin[cos
1
(1/4)].
56. Find the exact value of sin[tan
1
(1/2) cos
1
(4/5)].
In Questions 57–76, solve the equation by any means. Find
exact solutions when possible and approximate ones otherwise.
57. 2 sin x 1 58. sin x 3
/2
59. cos x 2
/2 60. cos x .5
61. tan x 1 62. tan x 3
63. sin 3x 3
/2 64. cos 4x .5
65. sin x .4 66. cos x .7
67. tan x 15 68. cot x .3
69. 2 sin
2
x 5 sin x 3 70. 4 cos
2
x 2 0
71. 2 sin
2
x 3 sin x 2
72. cos 2x cos x [Hint: First use an identity.]
73. sec
2
x 3 tan
2
x 13 74. sec
2
x 4 tan x 2
75. 2 sin
2
x sin x 2 0 76. cos
2
x 3 cos x 2 0
In Questions 77–80, solve the equation graphically.
77. 5 tan x 2 sin 2x 78. sin
3
x cos
2
x tan x 2
79. sin x sec
2
x 3
80. cos
2
x csc
2
x tan(x p/2) 5 0
81. Find all angles u with 0° u 360° such that sin u
.7133.
82. Find all angles u with 0° u 360° such that tan u
3.7321.
83. A cannon has a muzzle velocity of 600 feet per second. At
what angle of elevation should it be fired in order to hit a
target 3500 feet away? [Hint: Use the projectile equation
preceding Exercise 103 of Section 7.5.]
84. A weight hanging from a spring is set into motion (see Fig-
ure 6–69 on page 484), moving up and down. Its distance
(in centimeters) above or below the equilibrium point at
time t seconds is given by d 5 sin 3t 3 cos 3t. At what
times during the first 2 seconds is the weight at the equilib-
rium position (d 0)?
Chapter
7
Test
Sections 7.1–7.3
1. Prove: 1 sin x cos x tan x cos
2
x
2. Find the exact value of cos
5
1
p
2
.
3. Find the exact value of tan
3
8
p
.
4. Prove: cos
2
x cot
2
x cos
2
x cot
2
x
5. Simplify: sin(x y) sin x cos(x y) cos x
6. If sin x
4
4
0
1
and p x
3
2
p
, find the exact value of
(a) cos 2x (b) sin 2x (c) tan 2x
7. Prove: (sin
2
x 1)(cot
2
x 1) cot
2
x

8. If cos x
1
4
and p x
3
2
p
, then find the exact value
of cos
p
6
x
.
9. Simplify: 2 cos
2
2
x
1
10. Prove:
1
co
t x
ta
n
1
x
tan x
11. Prove: sin x sin(p x) 1 cos
2
x
12. If sin x .4 and
p
2
x p, find the exact values of
(a) sin
2
x
(b) cos
2
x
.
Sections 7.4 and 7.5
13. Find the exact value of cos
1
2
3
.
14. Find all solutions of the equation 7 cos x 5.
15. Find the exact value of cos
1
sin
p
4
.
570 CHAPTER 7 Trigonometric Identities and Equations
16. Find all solutions in [0, 2p) of the equation cos
2
x
7 cos x 7.
17. A rocket is fired straight up. The line of sight from an
observer 3 miles away makes an angle of t radians with the
horizontal. Find t when the rocket is 4 miles high.
18. Find all solutions of 2 sin
2
x
2
. Exact answers are
required.
19. Assume that
p
2
x
p
2
. Prove that cos
1
(sin x)
p
2
x.
20. When a projectile (such as a ball) leaves its starting point
at an angle of elevation of u radians with velocity v, the
horizontal distance d it travels is given by
d
3
v
2
2
sin 2u,
where d is measured in feet and v in feet per second. Suppose
an outfielder throws a baseball at a speed of 76 mph to the
catcher who is 170 feet away. At what angle of elevation
(in radians) was the ball thrown?

571
Jack Hollingsworth/Getty Images
DISCOVERY PROJECT 7 The Sun and the Moon
It has long been known that the cycles of the sun and the moon are periodic; that
is, the moon is full at regular intervals and new at regular intervals. The same is
true of the sun; the interval between the summer and winter solstices is also regu-
lar. It is therefore quite natural to use the sun and the moon to keep track of time,
and to study the interaction between the two to predict events such as full moons,
new moons, solstices, equinoxes, and eclipses. Indeed, these solar and lunar
events have consequences on the earth, including the succession of the seasons
and the severity of tides.
1. Thep following is a list of the days in 1999 when the moon was full. The
length of the lunar month is the length of time between full moons. Use
the data to approximate the length of the lunar month.
January 2 May 30 October 24
January 31 June 28 November 23
March 2 July 28 December 22
March 31 August 26
April 30 September 25
2. Write a function that has value 1 when the moon is full and 0 when the
moon is new. Measure the independent variable in days with January 2,
1999, set as time 0. Use a function of the form
m(x)
cos k
2
t 1
with period equal to the length of the lunar month.
Sun
Earth
Orbit
Orbit
Moon

572
DISCOVERY PROJECT 7
3. Use your function to predict the date of the first full moon of the 21st
century (in January of the year 2001). Does your function agree with the
actual date of January 9? If not, what could have caused the discrepancy?
4. The solar year is approximately 365.24 days long. Write a function s(x)
with period equal to the length of the solar year so that on the date of the
summer solstice, s(x) 1 and on the day of the winter solstice, s(x) 0.
The summer solstice in 1999 was June 21 and the winter solstice falls
midway between summer solstices.
5. If your functions s(x) and m(x) were accurate, when would you expect to
see the next full moon on the summer solstice?
6. How would you go about making your models s(x) and m(x) more
accurate?

TRIANGLE TRIGONOMETRY
Where are we?
Navigators at sea must determine their location.
Surveyors need to determine the height of a
mountain or the width of a canyon when direct
measurement isn’t feasible. A fighter plane’s
computer must set the course of a missile so that it
will hit a moving target. These and many similar
problems can be solved by using triangle
trigonometry. See Exercise 37 on page 605
and Exercise 33 on page 614.
573
Chapter
© Jerry Kobalenko/ Getty Images
10 16
A
B
c
C
110°

574
Chapter Outline
Interdependence of
Sections
8.1 Trigonometric Functions of Angles
8.1 ALTERNATE Trigonometric Functions of Angles
8.2 Applications of Right Triangle Trigonometry
8.3 The Law of Cosines
8.4 The Law of Sines
8.4.A Special Topics: The Area of a Triangle
Trigonometry was first used by the ancients to solve practical problems
in astronomy, navigation, and surveying that involved triangles. Trigono-
metric functions, as presented in Chapter 6, came much later. The early
mathematicians took a somewhat different viewpoint than we have used
up to now, but their approach is often the best way to deal with problems
involving triangles.
8.1 Trigonometric Functions of Angles
■ Evaluate trigonometric functions of angles.
■ Use right triangles to evaluate trigonometric functions.
■ Solve right triangles.
Trigonometric functions were defined in Chapter 6 as functions whose domains
consist of real numbers. In the classical approach, however, the domains of the
trigonometric functions consist of angles. In other words, instead of starting with
a number t and then moving to an angle of t radians, we start directly with the
angle, as summarized here.
trigonometric functions of real numbers
64444444444444744444444444448
——
——
1444444442444444443
trigonometric functions of angles
In this chapter (and hereafter, whenever convenient), we shall take this classical
approach and begin with angles. From there on, everything is essentially the
same. The values of the trigonometric functions are still numbers and are
obtained as before. For example, the point-in-the-plane description now reads
as follows.
Determine
sin t, cos t, tan t
Form an angle
of t radians
Begin with
a number t
8.3
8.1 8.2
8.4
Section Objectives
NOTE
If you have not read Chapter 6, use
Alternate Section 8.1 on page 584 in
place of this section.
All or part of this chapter may be
read before Chapter 6. Consult
the chart on page xiv for details.
Roadmap
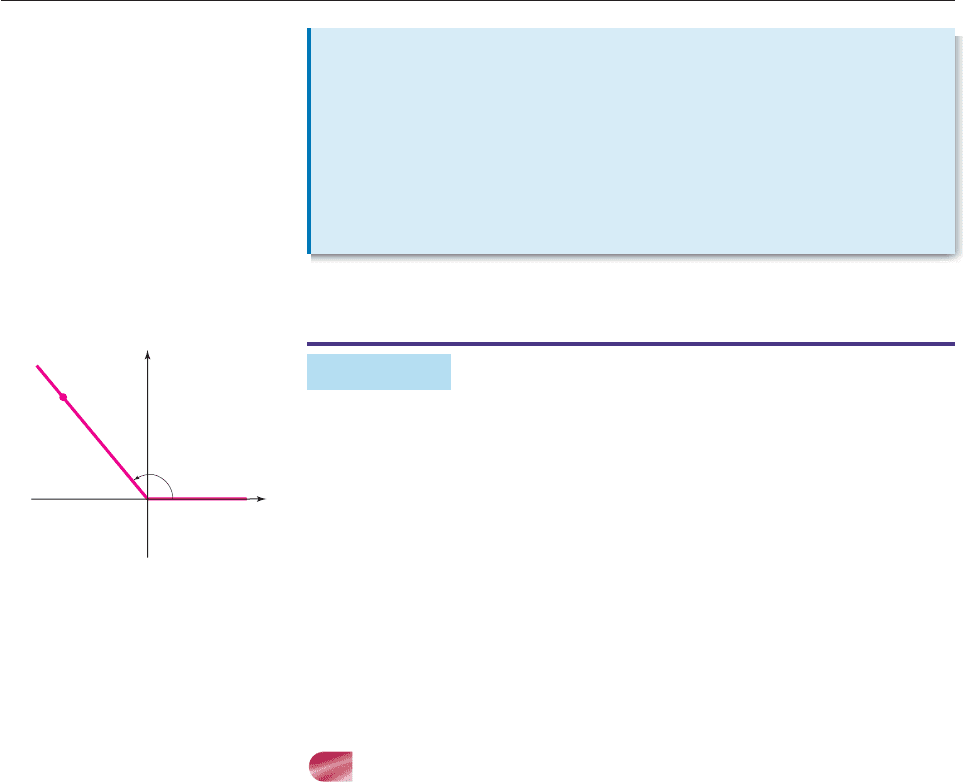
EXAMPLE 1
Evaluate the six trigonometric functions at the angle u shown in Figure 8–1.
SOLUTION We use (3, 4) as the point (x, y), so
r x
2
y
2
9 16
25 5.
Thus,
sin u
y
r
4
5
cos u
x
r
5
3
tan u
y
x
4
3
csc u
y
r
5
4
sec u
x
r
5
3
cot u
x
y
4
3
. ■
DEGREES AND RADIANS
Angles can be measured in either degrees or radians. If radian measure is used (as
was the case in Chapter 6), then everything is the same as before. For example,
sin 30 denotes the sine of an angle of 30 radians.
But when angles are measured in degrees (as will be done in the rest of this
chapter), new notation is needed. To denote the value of the sine function at an
angle of 30 degrees, we write
sin 30° [note the degree symbol]
The degree symbol here is essential for avoiding error. For example, an angle of
30 degrees is the same as an angle of p/6 radians. Therefore,
sin 30° sin p/6 1/2
This is not the same as sin 30 (the sine of an angle of 30 radians); a calculator in
radian mode shows that sin 30 .988.
The various identities proved in earlier sections are valid for angles mea-
sured in degrees, provided that p radians is replaced by 180°. For any angle u
measured in degrees for which the functions are defined, the following identi-
ties hold.
SECTION 8.1 Trigonometric Functions of Angles 575
Point-in-the-Plane
Description
Let u be an angle in standard position and let (x, y) be any point (except the
origin) on the terminal side of u. Let r
x
2
y
2
. Then, the values of
the six trigonometric functions of the angle u are given by
sin u
y
r
cos u
x
r
tan u
y
x
csc u
y
r
sec u
x
r
cot u
x
y
x
y
(−3, 4)
θ
Figure 8–1
