Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

BASIC EQUATIONS
We begin with basic equations, such as
sin x .39, cos x .2, tan x 3.
Basic equations can be solved by the methods illustrated in Examples 1–3.
EXAMPLE 1
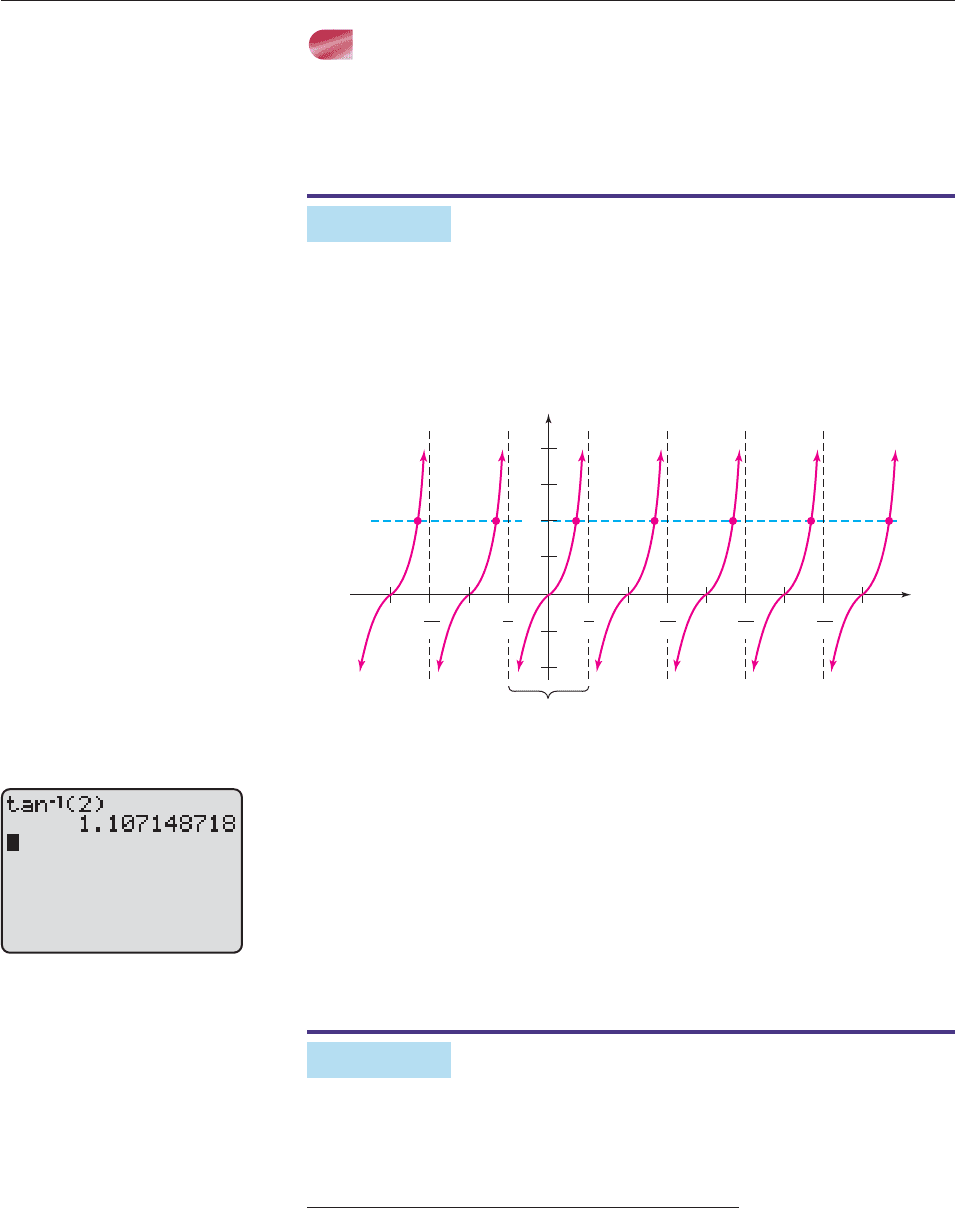
Solve tan x 2.
SOLUTION The equation can be solved graphically by graphing y tan x
and y 2 on the same coordinate axes and finding the intersection points. The x-
coordinate of every such point is a number whose tangent is 2, that is, a solution of
the equation.
Figure 7–20
Figure 7–20 shows that there is exactly one solution in each period of tan x. The
solution between p/2 and p/2 could be found graphically, but it’s faster to
compute tan
1
2 on a calculator.* The calculator then displays the number be-
tween p/2 and p/2 whose tangent is 2, namely, x 1.1071, as shown in Fig-
ure 7–21.
†
Since the tangent graph repeats its pattern with period p, all the other
solutions differ from this one by an integer multiple of p. Thus, all the solutions are
1.1071, 1.1071 p, 1.1071 2p, 1.1071 3p,etc.
These solutions are customarily written like this:
x 1.1071 kp (k 0, 1, 2, 3, . . .). ■
EXAMPLE 2
Solve tan
1
x 1.
SOLUTION We can construct a picture of the situation by replacing the hori-
zontal blue line through 2 in Figure 7–20 by a horizontal line through 1. As in
π
2
One period
−
x
y
π
−π
2
1
−1
2
3
−
3π
−2π 2ππ 3π 4π
2
3π
2
5π
2
7π
2
556 CHAPTER 7 Trigonometric Identities and Equations
Figure 7–21
*Unless stated otherwise, radian mode is used throughout this section.
†
You need not have read about inverse trigonometric functions in Section 7.4 to understand this
section. Here the calculator’s tan
1
key is used only to produce one number with the given tangent,
and similarly for the sin
1
and cos
1
keys.
Example 1, there is just one solution between p/2 and p/2. Our knowledge of
special values tells us that this solution is x p/4 (because tan(p/4) 1 by
Example 4 of Section 6.2). Since the tangent function has period p, the other so-
lutions differ from x p/4 by integer multiples of p. So all solutions are given by
x
p
4
kp (k 0, 1, 2, 3, . . .). ■
The techniques illustrated in Examples 1 and 2 apply in the general case.
Solving basic sine equations is similar to solving basic tangent equations, but
involves one additional step, as illustrated in the next example.
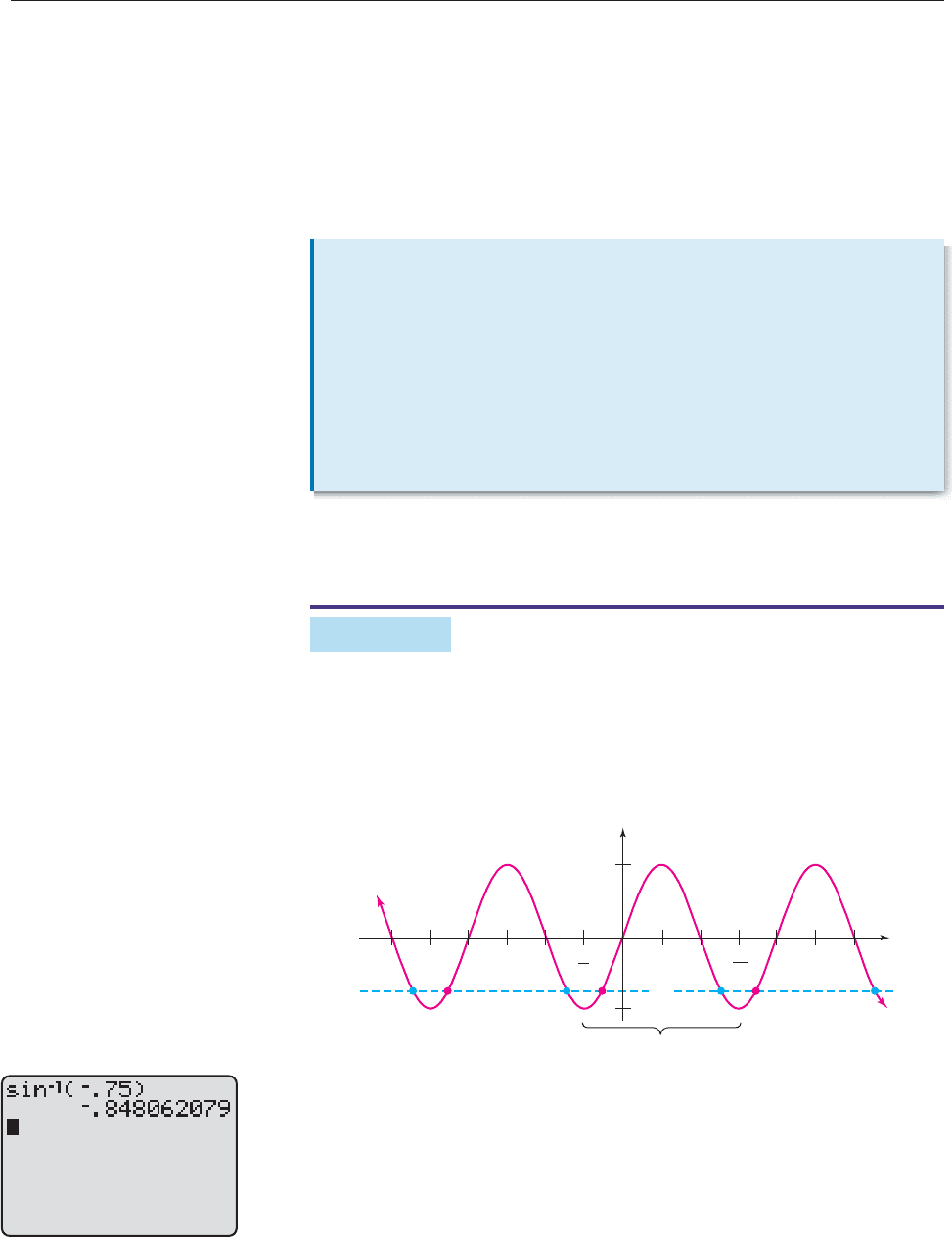
EXAMPLE 3
Solve sin x .75
SOLUTION The solutions are the x-coordinates of the points where the graphs
of y sin x and y .75 intersect (why?). Note that there are exactly two solu-
tions in every period of sin x (for instance, between p/2 and 3p/2).
Figure 7–22
Figure 7–22 shows that there is one solution between p/2 and p/2. It can be
found by computing sin
1
(.75) on a calculator. The calculator displays the
number between p/ 2 and p/2 whose sine is .75, namely x .8481, as
shown in Figure 7–23. Since the sine graph repeats is pattern with period 2p, all
of the following numbers are also solutions:
.8481, .8481 2p, .8481 4p, .8481 6p,etc.
−
x
y
π
2
−1
1
3π
2
−π−2π 2π
.75
one period
π
SECTION 7.5 Trigonometric Equations 557
Solving
tan x c
If c is any real number, then the equation
tan x c
can be solved as follows.
1. Find one solution u by using your knowledge of special values or by
computing tan
1
c on a calculator.
2. Then all solutions are given by
x u kp (k 0, 1, 2, 3, . . .).
Figure 7–23

These solutions correspond to the red intersection points in Figure 7–22, each of
which is 2p units from the next red point. As you can see, there are still more so-
lutions (corresponding to the blue points). One of them can be found by using the
identity that was proved in Example 2 of Section 7.2:
sin(p x) sin x.
Applying this identity with the solution x .8481 shows that
sin[p (.8481] sin(.8481) .75.
In other words, p (.8481) 3.9897 is also a solution of sin x .75. The
other solutions of the equation are
3.9897, 3.9897 2p, 3.9897 4p, 3.9897 6p, etc.,
corresponding to the blue intersection points in Figure 7–22, each of which is
2p units from the next blue point. Therefore, all the solutions of sin x 0.75 are
x .8481 2kp and x 3.9897 2kp
(k 0, 1, 2, 3, . . .). ■
The solution methods of Example 3 extend to the general case.
EXAMPLE 4
Solve sin v 2
/2 without using a calculator.
SOLUTION Our knowledge of special values shows that v p/4 is one solu-
tion (see Example 4 of Section 6.2). Hence, a second solution is
p v p
p
4
3
4
p
,
and all solutions are
v
p
4
2kp and v
3
4
p
2kp (k 0, 1, 2, 3, . . .). ■
558 CHAPTER 7 Trigonometric Identities and Equations
Solving
sin x c
If c is a number between 1 and 1, then the equation
sin x c
can be solved as follows.*
1. Find one solution u by using your knowledge of special values or by
computing sin
1
c on a calculator.
2. A second solution is p u.
3. All solutions are given by
x u 2kp and x (p u) 2kp (k 0, 1, 2, 3, . . .).
*Equations of the form sin x c, with |c| 1, have no solutions because the values of sine are always
between 1 and 1, as we saw in Chapter 6.

Solving basic cosine equations is similar to solving basic sine equations,
except that a different identity must be used to find the second solution.
EXAMPLE 5
Solve cos x 3
/2.
SOLUTION By graphing y cos x and y 3
/2 on the same screen (Fig-
ure 7–24), we see that there are two solutions of the equation between p and p
(one full period of cosine). The positive solution could be approximated by com-
puting cos
1
(3
/2) on a calculator. However, our knowledge of special values
provides an exact solution. Example 3 of Section 6.2 shows that cos(p/6)
3
/2. So one solution of the equation is x p/6. The negative angle identity
cos(x) cos x shows that the second solution is x p/6, because
cos
p
6
cos
p
6
2
3
.
Since the interval [p, p] is one full period of cosine, all the solutions of the
equation are
x
p
6
2kp and x
p
6
2kp (k 0, 1, 2, 3, . . .). ■
In the general case, we have the following result.
EXAMPLE 6
Find all solutions of sec x 8 in the interval [0, 2p).
SOLUTION Note that sec x 8 exactly when
co
1
s x
8 or, equivalently, cos x
1
8
.125.
Since cos
1
(.125) 1.4455, the solutions of cos x .125, and hence of sec x 8,
are
x 1.4455 2kp and x 1.4455 2kp
(k 0, 1, 2, 3, . . .).
SECTION 7.5 Trigonometric Equations 559
1.5
−1.5
π
−π
Figure 7–24
Solving
cos x c
If c is a number between 1 and 1, then the equation
cos x c
can be solved as follows.*
1. Find one solution u by using your knowledge of special values or by
computing cos
1
c on a calculator.
2. A second solution is u.
3. All solutions are given by
x u 2kp and x u 2kp (k 0, 1, 2, 3, . . .).
*Equations of the form cos x c, with |c| 1, have no solutions because the values of cosine are
always between 1 and 1, as we saw in Chapter 6.
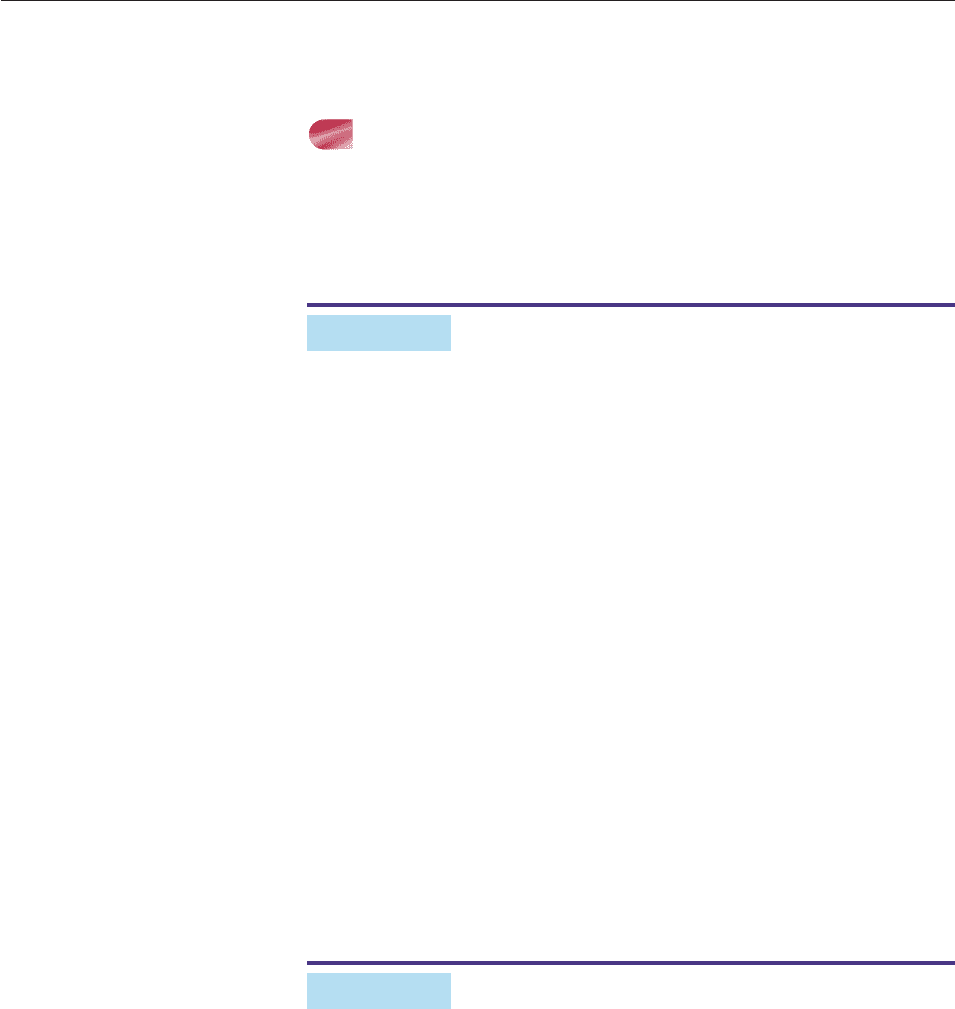
Of these solutions, the two between 0 and 2p are
x 1.4455 and x 1.4455 2p 4.8377. ■
ALGEBRAIC SOLUTION OF OTHER
TRIGONOMETRIC EQUATIONS
Many trigonometric equations can be solved algebraically by using substitution,
factoring, the quadratic formula, and identities to reduce the problem to an equiv-
alent one that involves only basic equations.
EXAMPLE 7
Solve exactly: sin 2x 2
/2.
SOLUTION First, let v 2x and solve the basic equation sin v 2
/2. As
we saw in Example 4, the solutions are
v
p
4
2kp and v
3
4
p
2kp (k 0, 1, 2, 3, . . .).
Since v 2x, each of these solutions leads to a solution of the original equation.
2x v
p
4
2kp or, equivalently, x
1
2
p
4
2kp
p
8
kp.
Similarly,
2x v
3
4
p
2kp or, equivalently, x
1
2
3
4
p
2kp
3
8
p
kp.
Therefore, all solutions of sin 2x 2
/2 are given by
x
p
8
kp and x
3
8
p
kp (k 0, 1, 2, 3, . . .).
The fact that the solutions are obtained by adding multiples of p rather than 2p is
a reflection of the fact that the period of sin 2x is p. ■
EXAMPLE 8
Solve 10 cos
2
x 3 sin x 9 0.
SOLUTION We first use the Pythagorean identity to rewrite the equation in
terms of the sine function.
10 cos
2
x 3 sin x 9 0
10(1 sin
2
x) 3 sin x 9 0
10 10 sin
2
x 3 sin x 9 0
10 sin
2
x 3 sin x 1 0.
560 CHAPTER 7 Trigonometric Identities and Equations

Now factor the left side:*
(2 sin x 1)(5 sin x 1) 0
2 sin x 1 0 or 5 sin x 1 0
2 sin x 1 5 sin x 1
sin x 1/2 sin x 1/5 .2.
Each of these basic equations is readily solved. We note that sin(p/6) 1/2, so
x p/6 and x p p/6 5p/6 are solutions of the first one. Since
sin
1
(.2) .2014, both x .2014 and x p (.2014) 3.3430 are
solutions of the second equation. Therefore, all solutions of the original equation
are given by
x
p
6
2kp, x
5
6
p
2kp,
x .2014 2kp, x 3.3430 2kp,
where k 0, 1, 2, 3, . . . . ■
EXAMPLE 9
Solve sec
2
x 5 tan x 2.
SOLUTION We use the Pythagorean identity sec
2
x 1 tan
2
x to obtain an
equivalent equation.
sec
2
x 5 tan x 2
sec
2
x 5 tan x 2 0
(1 tan
2
x) 5 tan x 2 0
tan
2
x 5 tan x 3 0.
If we let u tan x, this last equation becomes u
2
5u 3 0. Since the left side
does not readily factor, we use the quadratic formula to solve the equation.
u
5
2
13
.
Since u tan x, the original equation is equivalent to
tan x
5
2
13
.6972 or tan x
5
2
13
4.3028.
Solving these basic equations as above, we find that x .6089 is a solution of
the first and x 1.3424 is a solution of the second. Hence, the solutions of the
original equation are
x .6089 kp and x 1.3424 kp
(k 0, 1, 2, 3, . . .). ■
5
5
2
4
1
3
2
SECTION 7.5 Trigonometric Equations 561
*The factorization may be easier to see if you first substitute v for sin x, so that 10 sin
2
x 3 sin x 1
becomes 10v
2
3v 1 (2v 1)(5v 1).
EXAMPLE 10
Solve 5 cos x 3 cos 2x 3.
SOLUTION We use the double-angle identity: cos 2x 2 cos
2
x 1 as
follows.
5 cos x 3 cos 2x 3
Use double-angle identity: 5 cos x 3(2 cos
2
x 1) 3
Multiply out left side: 5 cos x 6 cos
2
x 3 3
Rearrange terms: 6 cos
2
x 5 cos x 6 0
Factor left side: (2 cos x 3)(3 cos x 2) 0
2 cos x 3 0 or 3 cos x 2 0
2 cos x 3 3 cos x 2
cos x
3
2
cos x
2
3
.
The equation cos x 3/2 has no solutions because cos x always lies between
1 and 1. A calculator shows that the solutions of cos x 2/3 are
x .8411 2kp and x .8411 2kp
(k 0, 1, 2, 3, . . .). ■
GRAPHICAL SOLUTION METHOD
When the techniques of the preceding examples are inadequate, trigonometric
equations may be solved by the following graphical procedure.
562 CHAPTER 7 Trigonometric Identities and Equations
Graphical Method
for Solving
Trigonometric Equations
1. Write the equation in the form f (x) 0.
2. Determine the period of p of f (x).
3. Graph f (x) over an interval of length p.
4. Use a graphical root finder to determine the x-intercepts of the graph in
this interval.
5. For each x-intercept u, all of the numbers
u kp (k 0, 1, 2, 3, . . .)
are solutions of the equation.
2
−4
0
2π
Figure 7–25
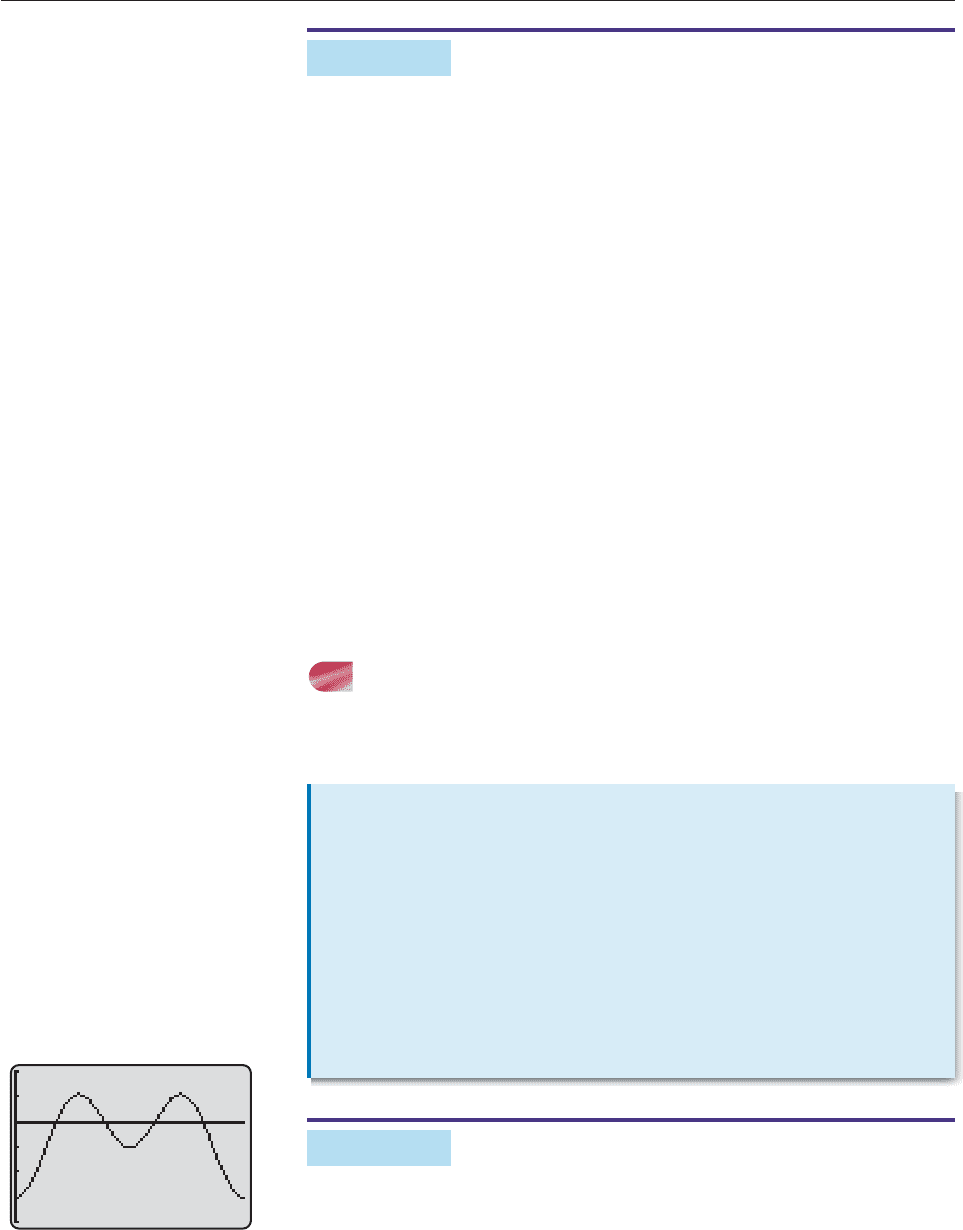
EXAMPLE 11
Solve 3 sin
2
x cos x 2 0.
SOLUTION Both sine and cosine have period 2p, so f (x) 3 sin
2
x cos x 2
also has period 2p. Figure 7–25 shows one full period of the graph of f. A graphical
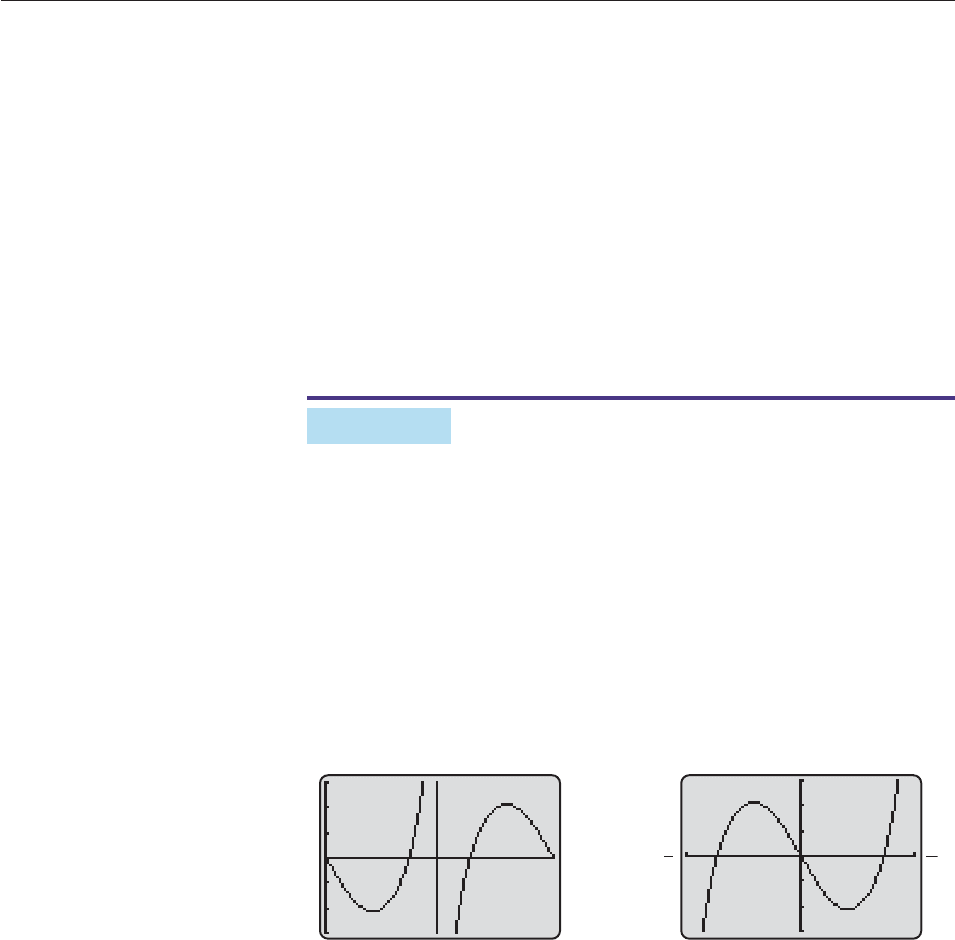
root finder shows that the four x-intercepts (solutions of the equation) in this
window are
x 1.1216, x 2.4459, x 3.8373, x 5.1616.
Since the graph repeats its pattern to the left and right, the other x-intercepts (so-
lutions) will differ from these four by multiples of 2p. For instance, in addition to
the solution x 1.1216, each of the following is a solution.
x 1.1216 2p, x 1.1216 4p, x 1.1216 6p, etc.
A similar analysis applies to the other solutions between 0 and 2p. Hence, all
solutions of the equation are given by
x 1.1216 2kp, x 2.4459 2kp, x 3.8373 2kp,
x 5.1616 2kp, where k 0, 1, 2, 3, . . . . ■
EXAMPLE 12
Solve tan x 3 sin 2x.
SOLUTION We first rewrite the equation as
tan x 3 sin 2x 0.
Both tan x and sin 2x have period p (see pages 472 and 478). Hence, the function
given by the left side of the equation, f (x) tan x 3 sin 2x, also has period p. The
graph of f on the interval [0, p) (Figure 7–26) shows an erroneous vertical line
segment at x p/2, where tangent is not defined, as well as x-intercepts at
the endpoints of the interval. Consequently, we use the more easily read graph f in
Figure 7–27, which uses the interval (p/2, p/2).
Figure 7–26 Figure 7–27
Even without the graph, we can verify that there is an x-intercept at the origin
because
f (0) tan 0 3 sin(2
0) 0.
A root finder shows that the other two x-intercepts in Figure 7–22 are
x 1.1503 and x 1.1503.
Since f(x) has period p, all solutions of the equation are given by
x 1.1503 kp, x 0 kp, x 1.1503 kp
(k 0, 1, 2, 3, . . .). ■
3
−3
π
−
2
π
2
3
−3
0
π
SECTION 7.5 Trigonometric Equations 563

564 CHAPTER 7 Trigonometric Identities and Equations
EXERCISES 7.5
In all exercises, find exact solutions if possible (as in Examples
2, 4, 5, and 7) and approximate ones otherwise. When a calcu-
lator is used, round your answers (but not any intermediate
results) to four decimal places.
In Exercises 1–10, find all solutions of the equation.
1. sin x .465
2. sin x .682
3. cos x .564
4. cos x .371
5. tan x .354
6. tan x 10
7. cot x 2.3 [Remember: cot x 1/tan x.]
8. cot x 3.5 9. sec x 1.6
10. csc x 6.4
In Exercises 11–14, approximate all solutions in [0, 2p) of the
given equation.
11. sin x .119 12. cos x .958
13. tan x 4 14. tan x 18
In Exercises 15–24, use your knowledge of special values to
find the exact solutions of the equation.
15. sin x
3
/2 16. 2 cos x
2
17. tan x
3
18. tan x 1
19. 2 cos x
3
20. sin x 0
21. 2 sin x 1 0 22. csc x
2
23. csc x 2 24. 2 sec x 4
In Exercises 25–34, find all angles u with 0° u 360° that
are solutions of the given equation. [Hint: Put your calculator
in degree mode and replace p by 180° in the solution algo-
rithms for basic equations.]
25. tan u 7.95 26. tan u 69.4
27. cos u .42 28. cot u 2.4
29. 2 sin
2
u 3 sin u 1 0
30. 4 cos
2
u 4 cos u 3 0
31. tan
2
u 3 0
32. 2 sin
2
u 1
33. 4 cos
2
u 4 cos u 1 0
34. sin
2
u 3 sin u 10
At the instant you hear a sonic boom from an airplane over-
head, your angle of elevation a to the plane is given by the
equation sin a 1/m, where m is the Mach number for the
speed of the plane (Mach 1 is the speed of sound, Mach 2.5
is 2.5 times the speed of sound, etc.). In Exercises 35–38, find
the angle of elevation (in degrees) for the given Mach number.
Remember that an angle of elevation must be between
0° and 90°.
35. m 1.1 36. m 1.6
37. m 2 38. m 2.4
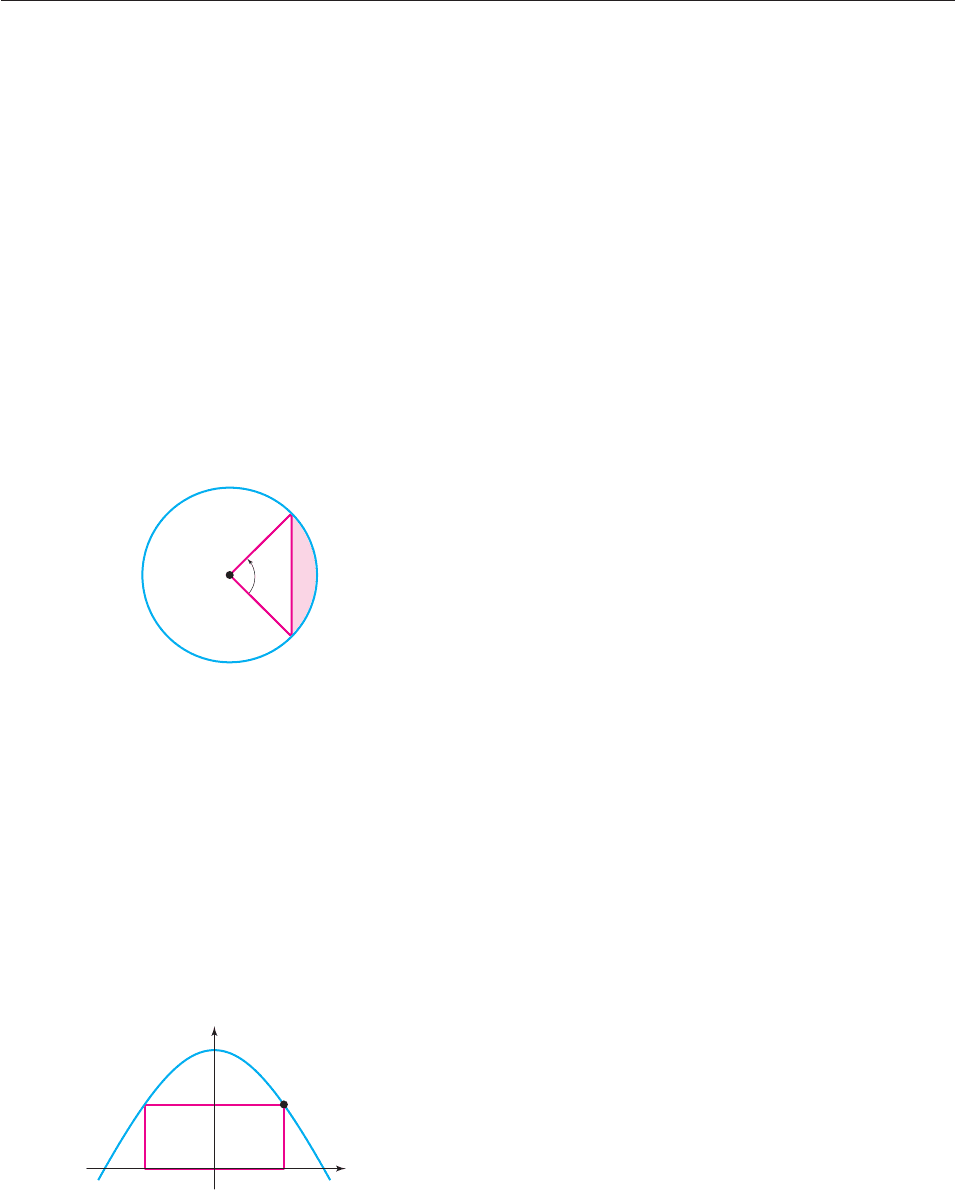
When a light beam passes from one medium to another (for
instance, from air to water), it changes both its speed and
direction. According to Snell’s Law of Refraction,
s
s
i
i
n
n
u
u
1
2
v
v
1
2
,
where v
1
is the speed of light in the first medium, v
2
its speed in
the second medium, u
1
the angle of incidence, and u
2
the angle
of refraction, as shown in the figure. The number v
1
/v
2
is
called the index of refraction. Use this information to do
Exercises 39–42.
39. The index of refraction of light passing from air to water is
1.33. If the angle of incidence is 38°, find the angle of
refraction.
40. The index of refraction of light passing from air to ordinary
glass is 1.52. If the angle of incidence is 17°, find the angle
of refraction.
41. The index of refraction of light passing from air to dense
glass is 1.66. If the angle of incidence is 24°, find the angle
of refraction.
42. The index of refraction of light passing from air to quartz is
1.46. If the angle of incidence is 50°, find the angle of
refraction.
2
θ
1
θ
Angle of incidence
Incident ray,
speed v
1
Angle of refraction
Refracted ray,
speed v
2
In Exercises 43–52, use an appropriate substitution (as in
Example 7) to find all solutions of the equation.
43. sin 2x
3
/2 44. cos 2x
2
/2
45. 2 cos
2
x
2
46. 2 sin
3
x
1
47. tan 3x
3
48. 5 sin 2x 2
49. 5 cos 3x 3 50. 2 tan 4x 16
51. 4 tan
2
x
8 52. 5 sin
4
x
4
Exercises 53–60, deal with a circle of radius r and a central
angle of t radians, (0 t p), as shown in the figure. The
length L of the chord determined by the angle and the area A
of the shaded segment are given by
L 2r sin
2
t
and A
r
2
2
(t sin t).
(See Exercise 108 for a proof of the first of these formulas.)
In Exercises 53–56, find the radian measure of the angle and
the area of the segment under the given conditions.
53. r 5 and L 8 54. r 8 and L 5
55. r 1 and L 1.5 56. r 10 and L 12.
In Exercises 57–60, find the radian measure of the angle and
the length L of the chord under the given conditions.
57. r 10 and A 50 58. r 1 and A .5
59. r 8 and A 20 60. r 5 and A 2
Exercises 61 and 62 deal with a rectangle inscribed in the
segment of the graph of f (x) 2 cos 2x shown in the figure.
61. (a) Find a formula for the area of the rectangle in terms
of x. [Hint: The length is 2x.]
(x, 2 cos 2x)
y
x
r
r
L
t
(b) For what values of x does the rectangle have an area of
1 square unit?
62. Use the formula in Exercise 61(a) to determine the value of
x that determines the rectangle with the largest possible
area. What is this maximum area?
In Exercises 63–88, use factoring, the quadratic formula, or
identities to solve the equation. Find all solutions in the
interval [0, 2p).
63. 3 sin
2
x 8 sin x 3 0
64. 5 cos
2
x 6 cos x 8
65. 2 tan
2
x 7 tan x 5 0
66. 3 sin
2
x 2 sin x 5
67. cot x cos x cos x [Be careful; see Exercise 109.]
68. tan x cos x cos x 69. cos x csc x 2 cos x
70. tan x sec x 3 tan x 0
71. 4 sin x tan x 3 tan x 20 sin x 15 0
[Hint: One factor is tan x 5.]
72. 25 sin x cos x 5 sin x 20 cos x 4
73. sin
2
x 2 sin x 2 0 74. cos
2
x 5 cos x 1
75. tan
2
x 1 3 tan x 76. 4 cos
2
x 2 cos x 1
77. 2 tan
2
x 1 3 tan x 78. 6 sin
2
x 4 sin x 1
79. sin
2
x 3 cos
2
x 0 80. sec
2
x 2 tan
2
x 0
81. sin 2x cos x 0 82. cos 2x sin x 1
83. 9 12 sin x 4 cos
2
x 84. sec
2
x tan x 3
85. cos
2
x sin
2
x sin x 0
86. 2 tan
2
x tan x 5 sec
2
x
87. sin
2
x
1 cos x 88. 4 sin
2
2
x
cos
2
x 2
In Exercises 89–100, solve the equation graphically.
89. 4 sin 2x 3 cos 2x 2
90. 5 sin 3x 6 cos 3x 1
91. 3 sin
3
2x 2 cos x
92. sin
2
2x 3 cos 2x 2 0
93. tan x 5 sin x 1
94. 2 cos
2
x sin x 1 0
95. cos
3
x 3 cos x 1 0 96. tan x 3 cos x
97. cos
4
x 3 cos
3
x cos x 1
98. sec x tan x 3
99. sin
3
x 2 sin
2
x 3 cos x 2 0
100. csc
2
x sec x 1
SECTION 7.5 Trigonometric Equations 565
