Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


EXAMPLE 5
Prove that
cos x cos y
1
2
[cos(x y) cos(x y)].
SOLUTION We begin with the more complicated right side and use the addi-
tion and subtraction identities for cosine to transform it into the left side.
1
2
[cos(x y) cos(x y)]
1
2
[(cos x cos y sin x sin y)
(cos x cos y sin x sin y)]
1
2
(cos x cos y cos x cos y)
1
2
(2 cos x cos y) cos x cos y. ■
The addition and subtraction identities for sine and cosine can be used to
obtain the following identities, as outlined in Exercise 38.
It is sometimes convenient to say that x is a number in the first quadrant if
0 x p/2, that x is a number in the second quadrant if p/2 x p, and so on.
EXAMPLE 6
Suppose x is a number in the first quadrant and y is a number in the third quadrant.
If sin x 3/4 and cos y 1/3, find the exact values of sin(x y) and
tan(x y) and determine in which quadrant x y lies.
SOLUTION We want to apply the addition identities for sine and tangent. To
do so we must first find cos x, tan x, sin y and tan y. Using the Pythagorean iden-
tity and the fact that cos x and tan x are positive when 0 x p/2, we have
cos x
1 si
n
2
x
1
3
4
2
1
1
9
6
1
7
6
4
7
,
tan x
c
s
o
in
s
x
x
3/
7
/
4
4
3
4
4
7
3
7
3
7
7
.
Since y lies between p and 3p/2, its sine is negative; hence,
sin y
1 co
s
2
y
1
1
3
2
8
9
3
8
2
3
2
,
tan y
c
s
o
in
s
y
y
2
1/
2
3
/3
2
3
2
3
1
2
2
.
526 CHAPTER 7 Trigonometric Identities and Equations
Addition and Subtraction
Identities for Tangent
tan(x y)
1
ta
n
t
x
a
n x
ta
ta
n
n
y
y
tan(x y)
1
ta
n
t
x
a
n x
ta
ta
n
n
y
y
The addition identities for sine and tangent now show that
sin(x y) sin x cos y cos x sin y
3
4
3
1
4
7
2
3
2
12
3
2
12
14
3
12
214
,
tan(x y)
1
ta
n
t
x
a
n x
ta
ta
n
n
y
y
.
The numerator of sin(x y) is negative and the denominator of tan(x y) is neg-
ative, as you can easily verify, so the sine and tangent of x y are negative num-
bers. The fourth quadrant is the only one in which both sine and tangent are neg-
ative (see the sign chart in Exercise 63 on page 451). Hence, x y must be in the
fourth quadrant, that is, in the interval (3p/2, 2p). ■
COFUNCTION IDENTITIES
Other special cases of the addition and subtraction identities are the cofunction
identities:
The first confunction identity is proved by using the identity for cos(x y)
with p/2 in place of x and x in place of y.
cos
p
2
x
cos
p
2
cos x sin
p
2
sin x (0)(cos x) (1)(sin x) sin x.
Since the first cofunction identity is valid for every number x, it is also valid with
the number p/2 x in place of x.
sin
p
2
x
cos
p
2
p
2
x
cos x.
Thus, we have proved the second cofunction identity. The others now follow from
these two. For instance,
tan
p
2
x
c
s
o
in
s
[
[
(
(
p
p
/
/
2
2
)
)
x
x
]
]
c
s
o
in
s
x
x
cot x.
37
142
7 614
37
7
142
7 6
7
14
3
7
7
22
1
3
7
7
(22
)
SECTION 7.2 Addition and Subtraction Identities 527
Cofunction
Identities
sin x cos
p
2
x
cos x sin
p
2
x
tan x cot
p
2
x
cot x tan
p
2
x
sec x csc
p
2
x
csc x sec
p
2
x
EXAMPLE 7
Verify that
cos(x
co
s x
p/2)
tan x.
SOLUTION Beginning on the left side, we see that the term cos(x p/2)
looks almost, but not quite, like the term cos(p/2 x) in the cofunction identity.
But note that (x p/2) p/2 x. Therefore,
c
s
o
in
s
x
x
[Cofunction identity]
tan x. [Reciprocal identity] ■
PROOF OF THE ADDITION
AND SUBTRACTION IDENTITIES
We first prove the subtraction identity for cosine:
cos(x y) cos x cos y sin x sin y.
If x y, then this is true by the Pythagorean identity:
cos(x x) cos 0 1 cos
2
x sin
2
x cos x cos x sin x sin x.
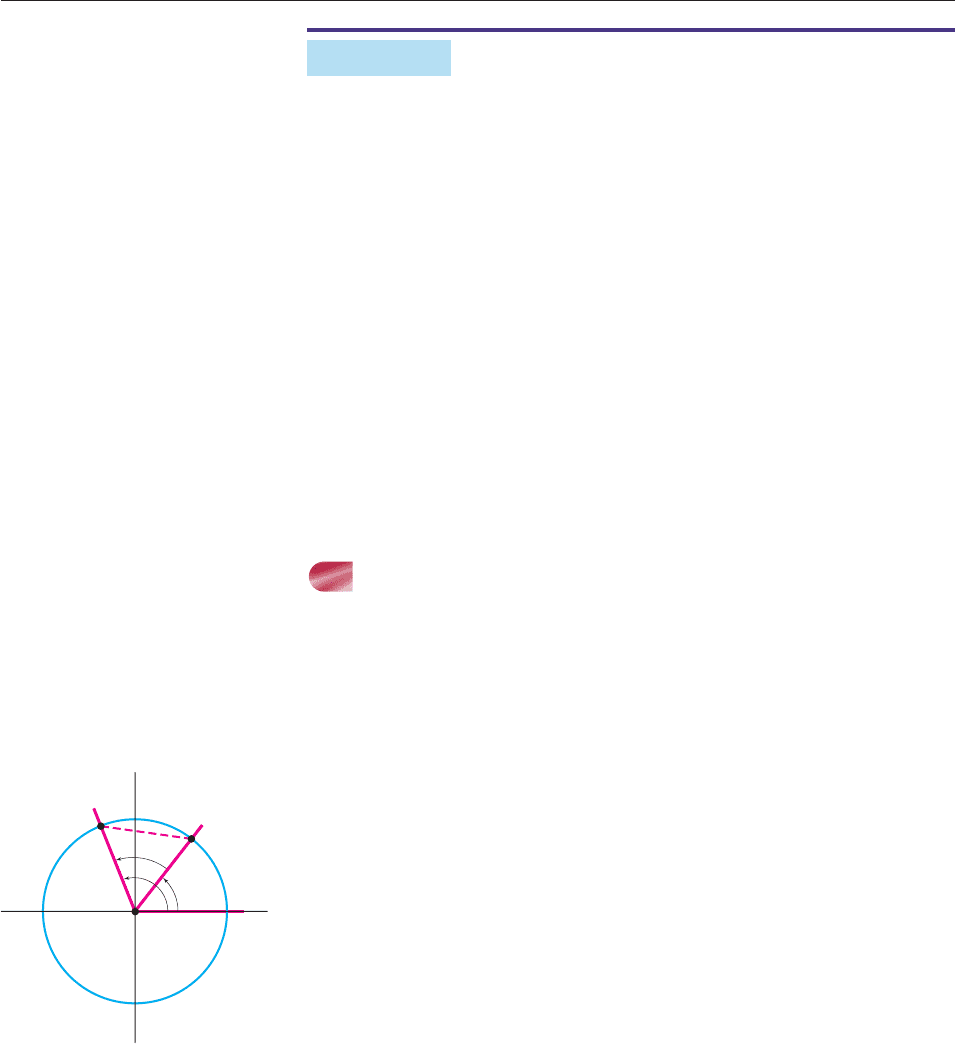
Next we prove the identity in the case when x y. Let P be the point where the
terminal side of an angle of x radians in standard position meets the unit circle and
let Q be the point where the terminal side of an angle of y radians in standard posi-
tion meets the circle, as shown in Figure 7–2. According to the definitions of sine
and cosine, P has coordinates (cos x, sin x) and Q has coordinates (cos y, sin y).
Using the distance formula, we have
Distance from P to Q
(cos x
cos
y)
2
(sin x
sin y)
2
cos
2
x
2 cos
x cos y
cos
2
y s
in
2
x
2 sin x
sin y
sin
2
y
(cos
2
x
sin
2
x) (c
os
2
y
sin
2
y)
2 c
os x co
s y 2
sin x s
in y
1 1
2 co
s x cos
y 2
sin x s
in y
2 2
cos x c
os y
2 sin x
sin y
.
The angle QOP formed by the two terminal sides has radian measure x y
(Figure 7.2). Rotate this angle clockwise until side OQ lies on the horizontal axis,
as shown in Figure 7–3. Angle QOP is now in standard position, and its terminal
side meets the unit circle at P. Since angle QOP has radian measure x y, the
cos
p
2
x
cos x
[Negative angle identity with
x
p
2
in place of x]
cos
x
p
2
cos x
cos
x
p
2
cos x
528 CHAPTER 7 Trigonometric Identities and Equations
x
y
x − y
O
Q
P
1
1
−1
−1
(cos y, sin y)
(cos x, sin x)
Figure 7–2
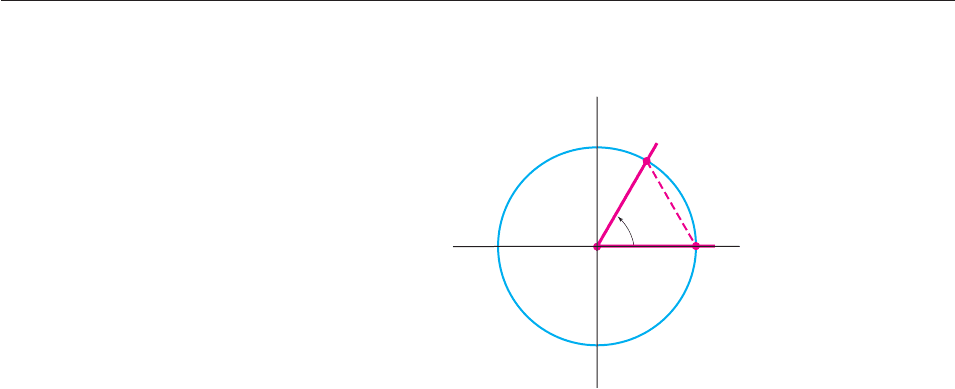
definitions of sine and cosine show that the point P, in this new location, has co-
ordinates (cos(x y), sin(x y)). Q now has coordinates (1, 0).
Figure 7–3
Using the coordinates of P and Q after the angle is rotated shows that
Distance from P to Q
[cos(x
y)
1]
2
[sin(x
y)
0]
2
cos
2
(x
y)
2 cos(
x y)
1
sin
2
(x
y)
cos
2
(x
y)
sin
2
(x
y)
2 cos(
x y)
1
1 2
cos(x
y) 1
[Pythagorean identity]
2 2
cos(x
y)
.
The two expressions for the distance from P to Q must be equal. Hence,
2 2
cos(x
y)
2 2
cos x c
os y
2 sin x
sin y
.
Squaring both sides of this equation and simplifying the result yields
2 2 cos(x y) 2 2 cos x cos y 2 sin x sin y
2 cos(x y) 2(cos x cos y sin x sin y)
cos(x y) cos x cos y sin x sin y.
This completes the proof of the subtraction identity for cosine when x y. If
y x, then the proof just given is valid with the roles of x and y interchanged; it
shows that
cos(y x) cos y cos x sin y sin x
cos x cos y sin x sin y.
The negative angle identity with x y in place of x shows that
cos(x
y) cos[(x y)] cos(y x).
Combining this fact with the previous one shows that
cos(x y) cos x cos y sin x sin y
in this case also. Therefore, the subtraction identity for cosine is proved.
Next, we prove the addition identity for cosine:
cos(x y) cos x cos y sin x sin y.
x − y
O
Q
P
(1, 0)
(cos (x − y), sin(x − y))
SECTION 7.2 Addition and Subtraction Identities 529

The proof uses the subtraction identity for cosine just proved and the fact that
x y x (y).
cos(x y) cos[x (y)]
cos x cos(y) sin x sin(y)
[Subtraction identity for cosine]
cos x cos y sin x(sin y) [Negative angle identities]
cos x cos y sin x sin y.
The proofs of the addition and subtraction identities for sine are in Exercises 36
and 37.
530 CHAPTER 7 Trigonometric Identities and Equations
EXERCISES 7.2
In Exercises 1–12, find the exact value.
1. cos
1
p
2
2. tan
1
p
2
3. sin
5
1
p
2
4. cos
5
1
p
2
5. cot
5
1
p
2
6. sin
7
1
p
2
7. tan
7
1
p
2
8. sin
1
1
1
2
p
9. cos
1
1
1
2
p
10. sin 75° [Hint: 75° 45° 30°.]*
11. sin 105°* 12. cos 165°*
In Exercises 13–18, rewrite the given expression in terms of
sin x and cos x.
13. sin
p
2
x
14. cos
x
p
2
15. cos
x
3
2
p
16. csc
x
p
2
17. sec(x p) 18. cot(x p)
In Exercises 19–24, simplify the given expression.
19. sin 3 cos 5 cos 3 sin 5
20. sin 37° sin 53° cos 37° cos 53°*
21. cos(x y) cos y sin(x y) sin y
22. sin(x y) cos y cos(x y) sin y
23. cos(x y) cos(x y)
24. sin(x y) sin(x y)
25. If sin x
1
3
and 0 x
p
2
, then sin
p
4
x
?
26. If cos x
1
4
and
p
2
x p, then cos
p
6
x
?
27. If cos x
1
5
and p x
3
2
p
, then sin
p
3
x
?
28. If sin x
3
4
and
3
2
p
x 2p, then cos
p
4
x
?
In Exercises 29–32, assume that sin x .8 and sin y .75
and
that x and y lie between 0 and p/2. Evaluate the given expressions.
29. sin(x y) 30. cos(x y)
31. sin(x y) 32. tan(x y)
33. The figure shows an angle of t radians. Prove that for any
number x,
5 sin(x t) 3 sin x 4 cos x.
34. The figure shows an angle of t radians. Prove that for any
number y,
13 cos(t y) 12 cos y 5 sin y.
35. If f (x) cos x and h is a fixed nonzero number, prove that:
f(x h
h
) f (x)
cos x
cos h
h
1
sin x
sin
h
h
.
36. Prove the subtraction identity for sine:
sin(x y) sin x cos y cos x sin y.
[Hint: Use the first cofunction identity*
sin(x y) cos
p
2
(x y)
cos
p
2
x
y
and the addition identity for cosine.]
(12, 5)
t
x
y
(3, 4)
t
x
y
*Skip Exercises 10–12 and 20 if you haven’t read Section 8.1.
*The cofunction identity may be validly used here because its proof on
page 527 depends only on the subtraction identity for cosine which was
proved in the text.

37. Prove the addition identity for sine:
sin(x y) sin x cos y cos x sin y.
[Hint: You may assume Exercise 36. Use the same method
by which the addition identity for cosine was obtained from
the subtraction identity for cosine in the text.]
38. Prove the addition and subtraction identities for the tangent
function (page 526). [Hint:
tan (x y)
c
s
o
in
s
(
(
x
x
y
y
)
)
.
Use the addition identities on the numerator and denomi-
nator; then divide both numerator and denominator by
cos x cos y and simplify.]
In Exercises 39–44, prove the identity.
39.
c
c
o
o
s
s(
x
x
c
os
y
y
)
1 tan x tan y
40.
s
s
i
i
n
n
(
x
x
s
in
y
y
)
cot x cot y
41.
s
s
i
i
n
n
(
x
x
s
in
y
y
)
cot y cot x
42.
c
s
o
in
s(
x
x
s
in
y
y
)
1 cot x cot y
43.
s
s
i
i
n
n(
x
x
c
os
y
y
)
1 cot x tan y
44.
s
s
i
i
n
n(
x
x
c
os
y
y
)
1 cot x tan y
45. If x is in the first and y is in the second quadrant,
sin x 24/25, and sin y 4/5, find the exact value of
sin(x y) and tan(x y) and the quadrant in which x y
lies.
46. If x and y are in the second quadrant, sin x 1/3, and
cos y 3/4, find the exact value of sin(x y),
cos(x y), tan(x y), and find the quadrant in which
x y lies.
47. If x is in the first and y is in the second quadrant,
sin x 4/5, and cos y 12/13, find the exact value of
cos(x y) and tan(x y) and the quadrant in which
x y lies.
48. If x is in the fourth and y is in the first quadrant,
cos x 1/3, and cos y 2/3, find the exact value of
sin(x y) and tan(x y) and the quadrant in which x y
lies.
49. Express sin(u v w) in terms of sines and cosines of
u, v, and w. [Hint: First apply the addition identity with
x u v and y w.]
SECTION 7.2 Addition and Subtraction Identities 531
50. Express cos(x y z) in terms of sines and cosines of
x, y, and z.
51. If x y p/2, show that sin
2
x sin
2
y 1.
52. Prove that cot(x y)
c
c
o
o
t
t
x
x
c
ot
c
y
o
t y
1
.
In Exercises 53–64, prove the identity.
53. sin(x p) sin x
54. cos(x p) cos x
55. cos(p x) cos x
56. tan(p x) tan x
57. sin(x p) sin x
58. cos(x p) cos x
59. tan(x p) tan x
60. sin x cos y
1
2
[sin(x y) sin(x y)]
61. sin x sin y
1
2
[cos(x y) cos(x y)]
62. cos x sin y
1
2
[sin(x y) sin(x y)]
63. cos(x y) cos(x y) cos
2
x cos
2
y sin
2
x sin
2
y
64. sin(x y) sin(x y) sin
2
x cos
2
y cos
2
x sin
2
y
In Exercises 65–74, determine graphically whether the equa-
tion could possibly be an identity (by choosing a numerical
value for y and graphing both sides). If it could, prove that
it is.
65.
c
si
o
n
s(
x
x
c
os
y
y
)
cot x tan y
66.
c
si
o
n
s(
x
x
c
os
y
y
)
cot x tan y
67. sin(x y) sin x sin y
68. cos(x y) cos x cos y
69.
s
s
i
i
n
n
(
(
x
x
y
y
)
)
t
t
a
a
n
n
x
x
t
t
a
a
n
n
y
y
70.
s
s
i
i
n
n
(
(
x
x
y
y
)
)
c
c
o
o
t
t
y
y
c
c
o
o
t
t
x
x
71.
c
c
o
o
s
s
(
(
x
x
y
y
)
)
c
c
o
o
t
t
x
x
t
t
a
a
n
n
y
y
72.
c
c
o
o
s
s
(
(
x
x
y
y
)
)
c
c
o
o
t
t
y
y
t
t
a
a
n
n
x
x
73. tan(x y) tan x tan y
74. cot(x y) cot x cot y
532 CHAPTER 7 Trigonometric Identities and Equations
■ Find the angle between two lines.
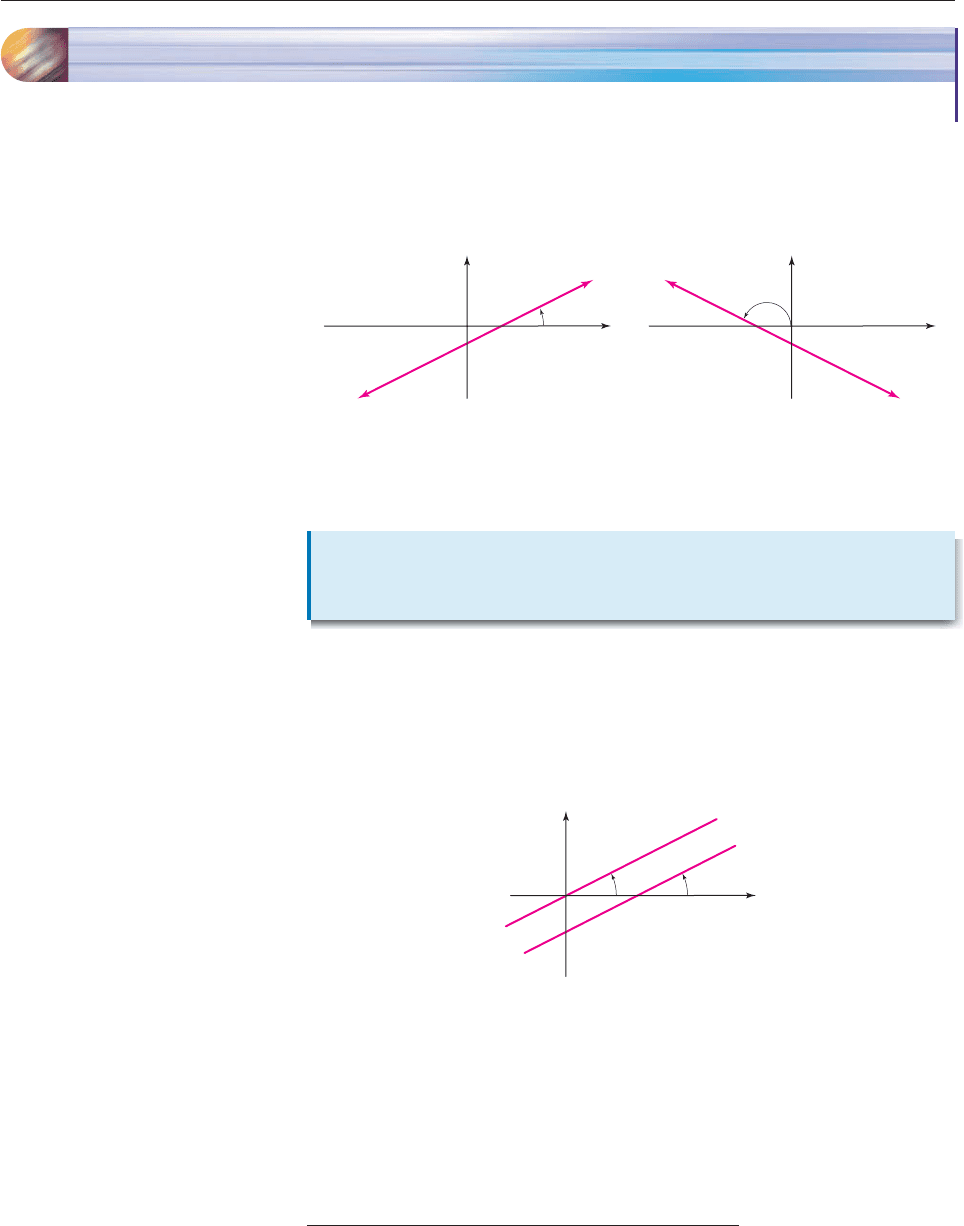
If L is a nonhorizontal straight line, the angle of inclination of L is the angle u
formed by the part of L above the x-axis and the x-axis in the positive direction, as
shown in Figure 7–4.
Figure 7–4
The angle of inclination of a horizontal line is defined to be u 0. Thus, the radian
measure of the angle of inclination of any line satisfies 0 u p. Furthermore,
Proof First, suppose L is horizontal. Then L has slope 0 and angle of incli-
nation u 0. Hence,
tan u tan 0 0 slope L.
Next, suppose L is not horizontal. L is parallel to a line M through the origin, as
shown in Figure 7–5.*
Figure 7–5
Basic facts about parallel lines show that M has the same angle of inclination u
as L. Furthermore, M lies on the terminal side of an angle of u radians in standard
position. Therefore, as we proved in Section 6.4,
slope M tan u.
Since parallel lines have the same slope, we have
slope L slope M tan u. ■
θ
L
M
θ
x
y
θ
x
y
L
θ
x
y
L
7.2.A SPECIAL TOPICS Lines and Angles
Section Objective
Angle of
Inclination
If L is a nonvertical line with an angle of inclination of u radians, then
tan u slope of L.
*Figure 7–5 illustrates the case when u is acute and L lies to the right of M. The pictures are different
in the other possible cases, but the argument is the same.
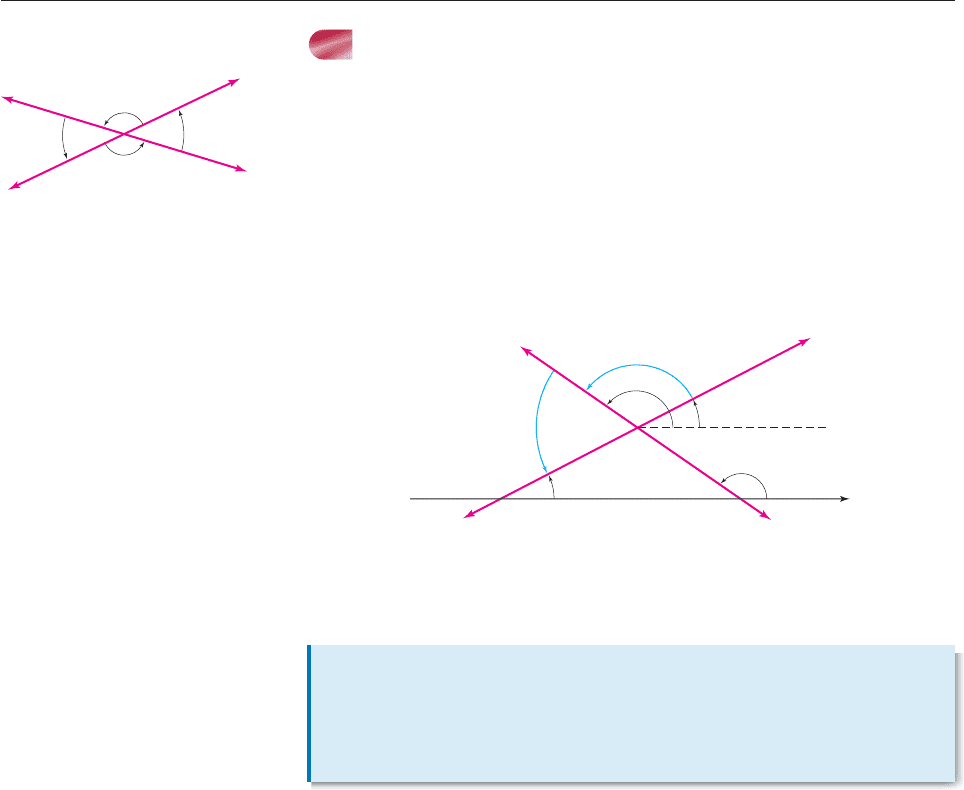
ANGLES BETWEEN TWO LINES
If two lines intersect, then they determine four angles with vertex at the point of
intersection, as shown in Figure 7–6. If one of these angles measures u radians,
then each of the two angles adjacent to it measures p u radians. (Why?) The
fourth angle also measures u radians by the vertical angle theorem from plane
geometry.
The angles between intersecting lines can be determined from the angles of
inclination of the lines. Suppose L and M have angles of inclination a and b,
respectively, such that b a. Basic facts about parallel lines, as illustrated in
Figure 7–7, show that b a is one angle between L and M and p (b a) is
the other one.
Figure 7–7
The angle between two lines can also be found from their slopes by using this
fact.
Proof Suppose the line with slope k has angle of inclination a and the line
with slope m has angle of inclination b. Then
tan a k and tan b m.
If b a, then u b a is one angle between the lines. By the subtraction iden-
tity for tangent,
tan u tan(b a)
1
ta
n
t
b
an
b
ta
ta
n
n
a
a
1
m
m
k
k
.
The other angle between the lines is p u, and
tan(p u) tan(u) [tangent has period p]
tan u [negative angle identity]
1
m
m
k
k
.
By the definition of absolute value,
1
m
m
k
k
1
m
m
k
k
,
x
M
L
α
α
β
β − α
π − (β − α)
β
SPECIAL TOPICS 7.2.A Lines and Angles 533
θ
θ
π −
θ
π −
θ
Figure 7–6
Angle Between
Two Lines
If two nonvertical, nonperpendicular lines have slopes m and k, then one
angle u between them satisfies
tan u
1
m
m
k
k
.
whichever is positive. Thus, the tangent of one of the angles u or p u is
1
m
m
k
k
.
This completes the proof when b a. The proof when a b is similar. ■
EXAMPLE 1
Find the angle between a line L with slope 8 and a line M of slope 3.
SOLUTION One angle u between the lines satisfies
tan u
1
8
8
(
(
3
3
)
)
1
2
1
3
1
2
1
3
.
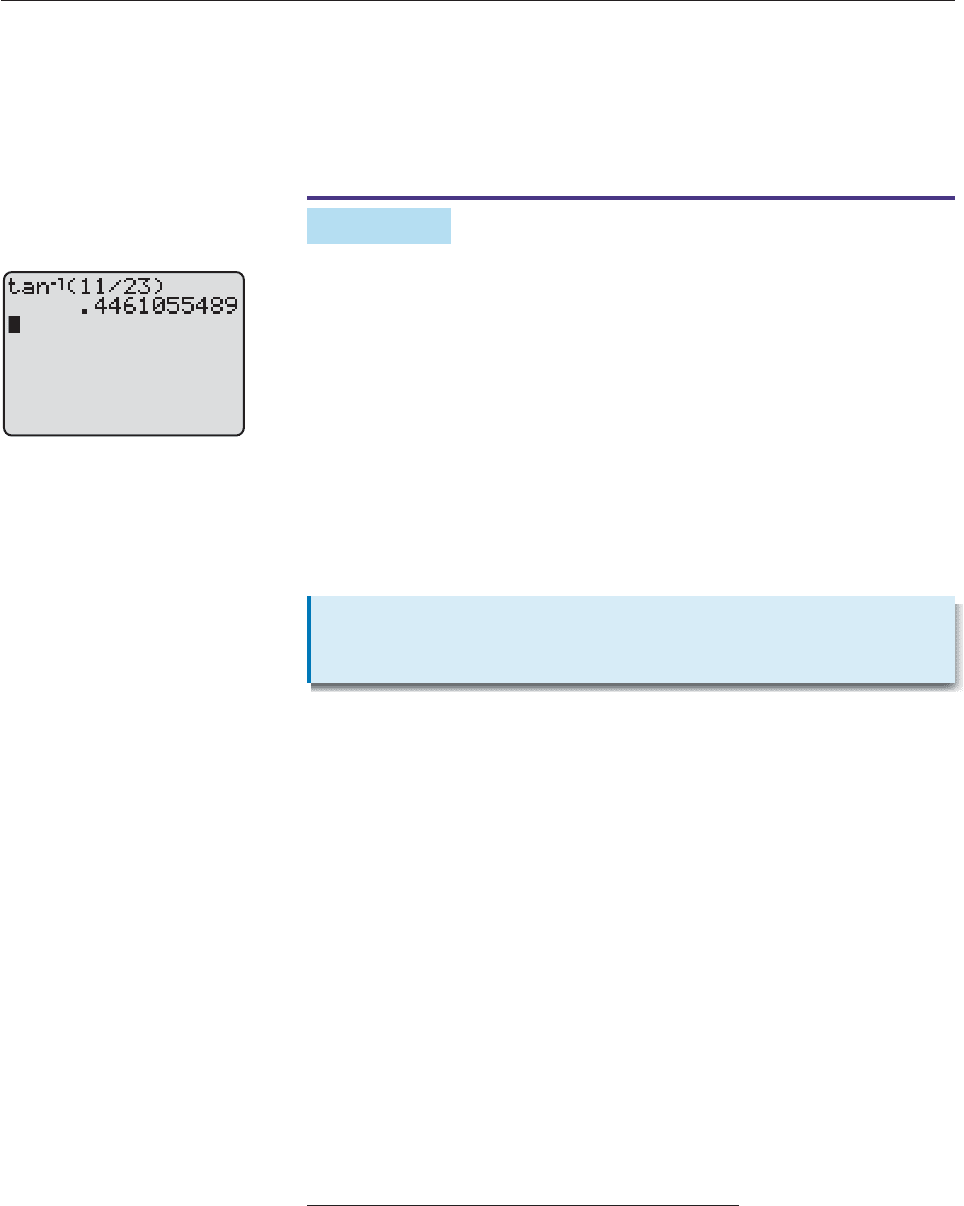
Although you could solve the equation tan u 11/23 graphically, it is easier to
use the TAN
1
key on your calculator. When you key in TAN
1
(11/23), the cal-
culator displays an angle between 0 and p/2 radians such that tan u 11/23, as
in Figure 7–8.* Therefore, u .4461 radians. ■
We can now prove the following fact, which was first presented in Section 1.4.
Proof First, suppose L and M are perpendicular. We must show that km 1.
If a and b (with b a) are the angles of inclination of L and M, then b a is the
angle between L and M, so b a p/2, or, equivalently, b a p/2. There-
fore, by the addition identities for sine and cosine,
m tan b tan
a
p
2
c
s
o
in
s
[
[
a
a
(
(
p
p
/
/
2
2
)
)
]
]
c
s
o
in
s
a
a
cot a
ta
n
1
a
k
1
.
Thus, m 1/k, and hence, mk 1.
Now suppose that mk 1. We must show that L and M are perpendicular.
If L and M are not perpendicular, then neither of the angles between them is p/2.
sin a(0) cos a(1)
cos a(0) sin a(1)
sin a cos(p/2) cos a sin(p/2)
cos a cos(p/2) sin a sin(p/2)
534 CHAPTER 7 Trigonometric Identities and Equations
Figure 7–8
*Tan
1
(x) denotes the inverse tangent function, which is explained in Section 7.4. In this context,
using the TAN
1
key is the electronic equivalent of searching through a table of tangent values until
you find a number whose tangent is 11/23.
Slope Theorem
for Perpendicular Lines
Let L be a line with slope k and M a line with slope m. Then
L and M are perpendicular exactly when km 1.

In this case, if u is either of the angles between L and M, then tan u is a well-
defined real number. But we know that one of these angles must satisfy
tan u
1
m
m
k
k
1
m
(
k
1)
m
0
k
,
which is not defined. This contradiction shows that L and M must be perpen-
dicular. ■
SECTION 7.3 Other Identities 535
EXERCISES 7.2.A
In Exercises 1–6, find tan u, where u is the angle of inclination
of the line through the given points.
1. (1, 2), (3, 5) 2. (0, 4), (5, 1)
3. (1, 4), (6, 0) 4. (4, 2), (3, 2)
5. (3, 7), (3, 5) 6. (0, 0), (4, 5)
In Exercises 7–13, find one of the angles between the straight
lines L and M.
7. L has slope 3/2 and M has slope 1.
8. L has slope 1 and M has slope 3.
9. L has slope 1 and M has slope 0.
10. L has slope 2 and M has slope 3.
11. (3, 2) and (5, 6) are on L; (0, 3) and (4, 0) are on M.
12. (1, 2) and (3, 3) are on L; (3, 3) and (6, 1) are on M.
13. L is parallel to the line with equation y 3x 2 and M is
perpendicular to the line with equation y .5x 1.
14. If u is an angle between two nonperpendicular lines with
slopes m and k, respectively, and tan u
1
m
m
k
k
,
explain why u is an acute angle. [Hint: For what values of u
is tan u positive?]
7.3 Other Identities
■ Use the double-angle, power-reducing, and half-angle identities
to evaluate and simplify trigonometric functions.
■ Use the product-to-sum and sum-to-product identities to prove
other identities.
We now present a variety of identities that are special cases of the addition and
subtraction identities of Section 7.2, beginning with
Proof Let x y in the addition identities:
sin 2x sin(x x) sin x cos x cos x sin x 2 sin x cos x,
cos 2x cos(x x) cos x cos x sin x sin x cos
2
x sin
2
x,
tan 2x tan(x x)
1
ta
n
t
x
a
n x
ta
ta
n
n
x
x
1
2
ta
t
n
an
x
2
x
. ■
Section Objectives
Double-Angle
Identities
sin 2x 2 sin x cos x
cos 2x cos
2
x sin
2
x
tan 2x
1
2
ta
t
n
an
x
2
x
