Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


496 CHAPTER 6 Trigonometric Functions
EXERCISES 6.5.A
In Exercises 1–6, estimate constants A, b, c such that
f(t) A sin(bt c).
1. f(t) sin t 2 cos t
2. f(t) 3 sin t 2 cos t
3. f(t) 2 sin 4t 5 cos 4t
4. f(t) 3 sin(2t 1) 4 cos(2t 3)
5. f(t) 5 sin(3t 2) 2 cos(3t 1)
6. f(t) .3 sin(2t 4) .4 cos(2t 3)
In Exercises 7–16, find a viewing window that shows a com-
plete graph of the function.
7. g(t) (5 sin 2t)(cos 5t) 8. h(t) e
sin t
9. f(t) t/2 cos 2t
10. g(t) sin
3
t
2
2 cos
4
t
2
11. h(t) sin 100t cos 50t
12. f (t) 3 sin(200t 1) 2 cos(300t 2)
13. g(t) 6 sin(250pt 5) 3 cos(400pt 7)
14. h(t) 4 sin(600pt 3) 6 cos(500pt 3)
15. f (t) 4 sin .2pt 8 cos .1pt
16. g(t) 9 sin .05pt 5 cos .04pt
In Exercises 17–24, describe the graph of the function verbally
(including such features as asymptotes, undefined points, am-
plitude and number of waves between 0 and 2p, etc.) as in Ex-
amples 4–6. Find viewing windows that illustrate the main fea-
tures of the graph.
17. g(t) sin e
t
18. h(t)
1
co
s2
t
t
2
19. f(t) t
cos t 20. g(t) e
t
2
/8
sin 2pt
21. h(t)
1
t
sin t 22. f (t) t sin
1
t
23. g(t) ln cos t 24. h(t) ln sin t 1
25. At a beach in Maui, Hawaii, the level of the tides is approx-
imated by
f (t) .7 sin(.52t 1.3728) .73 cos(.26t .6864) 1.4,
where t is measured in hours and f (t) in feet.
(a) Graph the tide function over a three-day period.
(b) At approximately what times during the day does the
highest tide occur? The lowest?
(c) What is the period of this function?
6.6 Other Trigonometric Functions
■ Define and graph the cotangent, secant and cosecant functions.
■ Use the point-in-the-plane description of these functions.
■ Apply the periodicity and Pythagorean identities for these
functions.
This section introduces three more trigonometric functions. It is divided into three
parts, each of which may be covered earlier, as shown in the table.
Section Objectives
Subsection of May be covered
Section 6.6 at the end of
Part I Section 6.2
Part II Section 6.3
Part III Section 6.4
SECTION 6.6 Other Trigonometric Functions 497
Definition of Cotangent,
Secant, and
Cosecant Functions
Value of Function
Name of Function at t Is Denoted Rule of Function
contangent cot t cot t
c
s
o
in
s
t
t
secant sec t sec t
co
1
s t
cosecant csc t csc t
si
1
n t
Function Domain
f (t) cot t All real numbers except
0, p, 2p, 3p, . . .
g(t) sec t All real numbers except
p/2, 3p/2, 5p/2, . . .
h(t) csc t All real numbers except
0, p, 2p, 3p, . . .
*This identity is valid except for t p/2, 3p/2, 5p/2, . . . . At these values, cos t 0 and
sin t 1, so cot t 0, but tan t is not defined.
PART I: Definitions and Descriptions
The three remaining trigonometric functions are defined in terms of sine and
cosine, as follows.
The domain of each function consists of all real numbers for which the denomi-
nator is not 0. The graphs of the sine and cosine function in Section 6.4 show that
sin t 0 only when t 0, p, 2p, 3p, . . . and cos t 0 only when
t p/2, 3p/2, 5p/2, . . . . So the domains of cotangent, secant, and cose-
cant are as follows.
The values of these functions may be approximated on a calculator by using
the SIN and COS keys. For instance,
cot(3.1)
c
s
o
in
s
(
(
3
3
.
.
1
1
)
)
24.0288, sec 7
co
1
s7
1.3264,
csc 18.5
sin
1
18.5
2.9199.
The cotangent function can also be evaluated with the TAN key, by using this fact:
cot t
c
s
o
in
s
t
t
ta
1
n t
.
*
For example,
cot(5)
tan(
1
5)
.2958.
1
c
s
o
in
s
t
t
CAUTION
The calculator keys labeled SIN
1
,
COS
1
, and TAN
1
do not denote the
functions 1/sin t, 1/cos t, and
1/tan t. For instance, if you key in
COS
1
7 ENTER
you will get an error message, not the
number sec 7, and if you key in
TAN
1
5 ENTER
you will obtain 1.3734, which is not
cot(5).
EXAMPLE 1
A batter hits a baseball. The ball is three feet above the ground and leaves the bat
with an initial velocity of 100 feet per second at an angle of t radians from the hor-
izontal. According to physics, the ball reaches a maximum height of
156
s
.2
e
5
c
2
t
t
an
2
t
3 feet.*
What is the maximum height of the ball when it leaves the bat at an angle of .6
radians?
SOLUTION Use a calculator to evaluate the formula for t .6. The maximum
height is
156
s
.2
e
5
c
2
ta
.6
n
2
.6
3 3 156.25(tan .6)
2
(cos .6)
2
3
52.816 feet. ■
These new trigonometric functions may be evaluated exactly at any integer
multiple of p/3, p/4, or p/6.
EXAMPLE 2
Evaluate the cotangent, secant, and cosecant functions at t p/3.
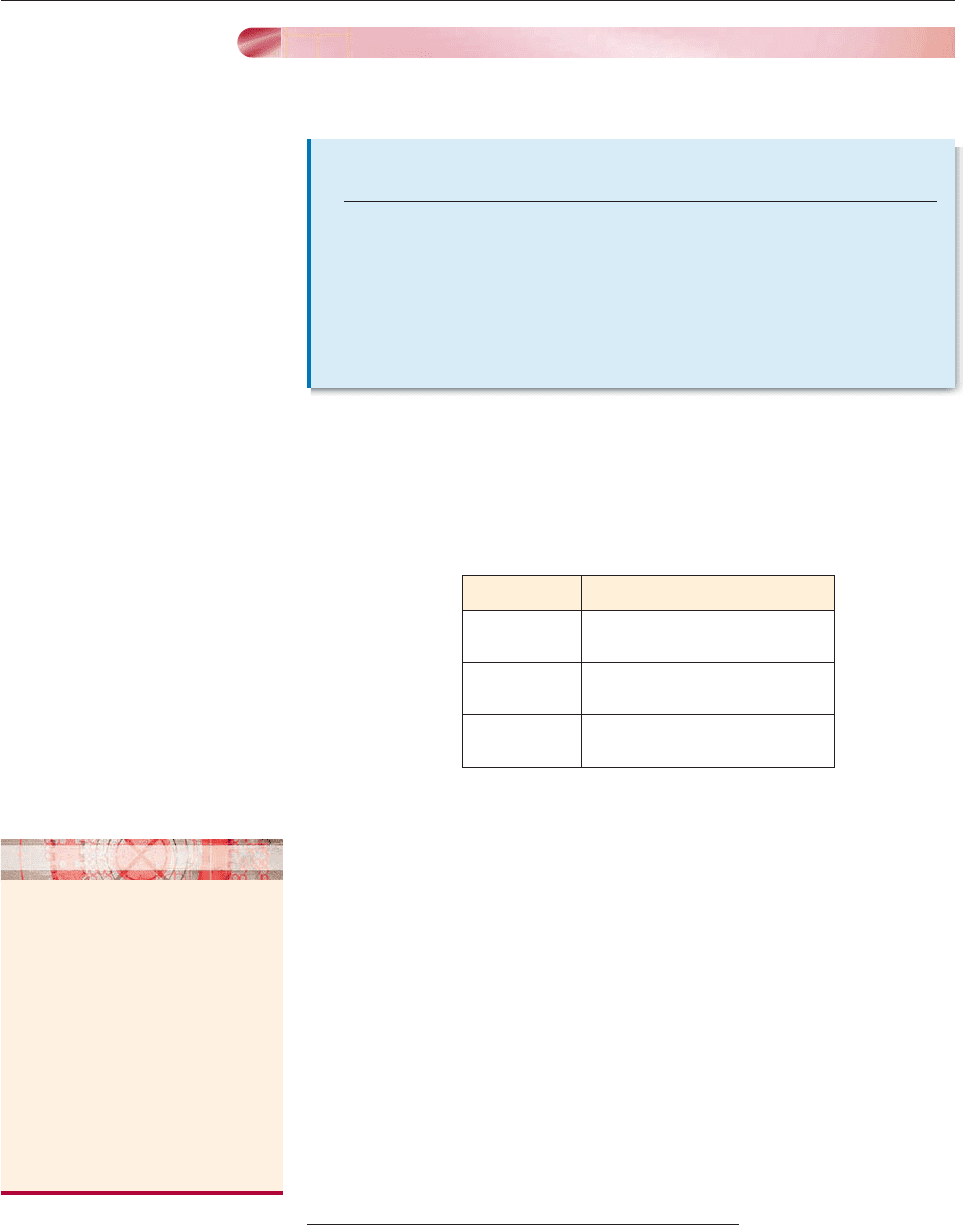
SOLUTION Let P be the point where the terminal side of an angle of p/3
radians in standard position meets the unit circle (Figure 6–82). Draw the vertical
line from P to the x-axis, forming a right triangle with hypotenuse 1, angles of
p/3 and p/6 radians, and sides of lengths of 1/2 and 3
/2 as explained on
page 445. Then P has coordinates (1/2, 3
/2), and by definition,
sin
p
3
y-coordinate of P 3
/2,
cos
p
3
x-coordinate of P 1/2.
Therefore,
csc
p
3
sin(p
1
/3)
2
3
3
,
sec
p
3
cos(
1
p/3)
1/
1
2
2,
cot
p
3
c
s
o
in
s
(
(
p
p
/
/
3
3
)
)
3
3
. ■
ALTERNATE DESCRIPTIONS
The point-in-the-plane description of sine, cosine, and tangent readily extends to
these new functions.
1
3
1/2
3
/2
2
3
1
3
/2
156.25 tan
2
.6
cos
1
2
.6
498 CHAPTER 6 Trigonometric Functions
*Wind resistance is ignored here.
1
2
3
1
1
1
2
π
6
π
3
P
y
Figure 6–82
These statements are proved by using the similar descriptions of sine and cosine.
For instance,
cot t
c
s
o
in
s
t
t
x
y
/
/
r
r
x
y
.
The proofs of the other statements are similar.
EXAMPLE 3
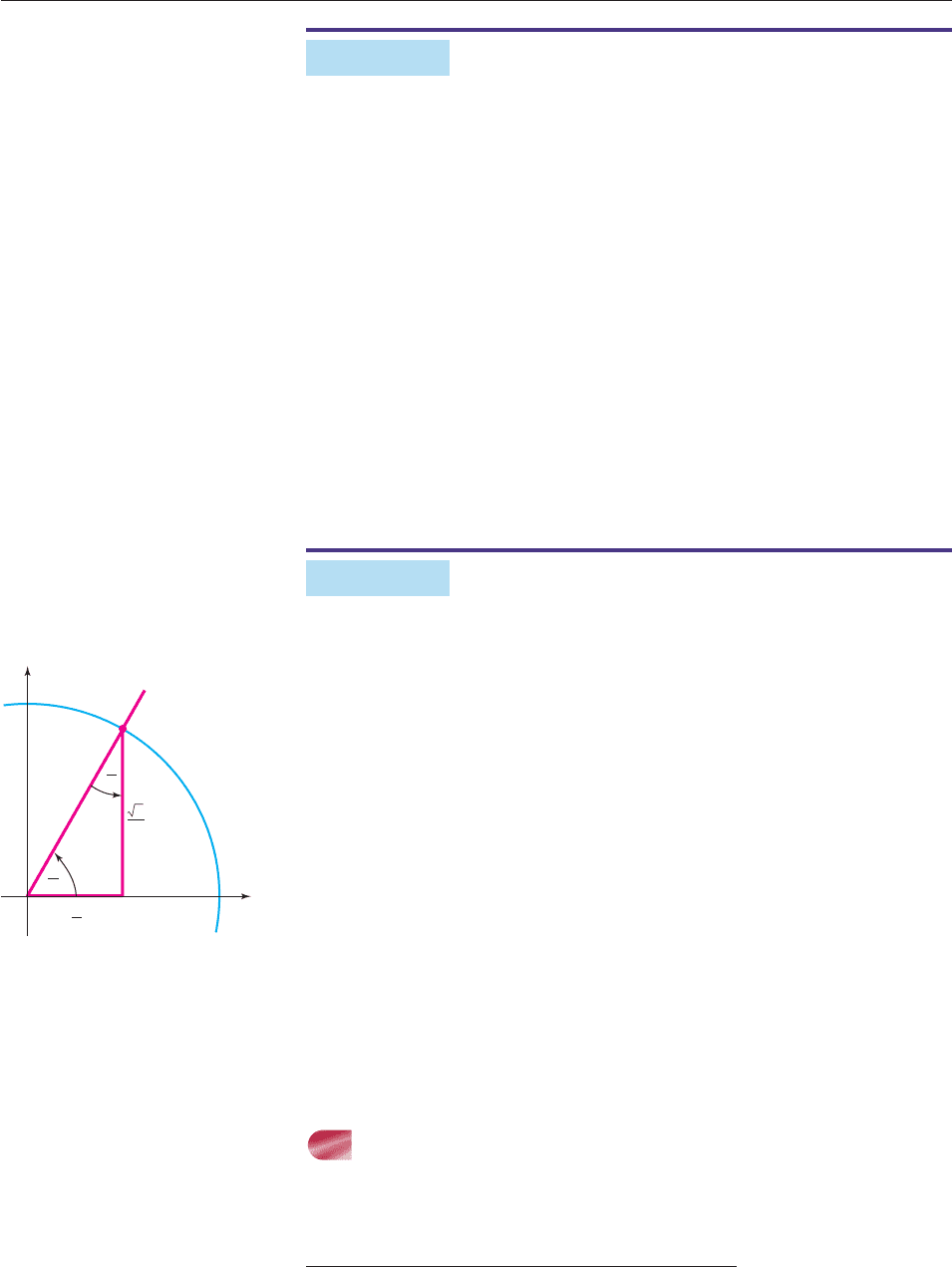
Evaluate all six trigonometric functions at t 3p/4.
SOLUTION The terminal side of an angle of 3p/4 radians in standard position
lies on the line y x, as shown in Figure 6–83. We shall use the point
(1, 1) on this line to compute the function values. In this case,
r
x
2
y
2
(1)
2
1
2
2
.
Therefore,
sin
3
4
p
y
r
2
2
cos
3
4
p
x
r
2
2
tan
3
4
p
y
x
1
1
1 csc
3
4
p
y
r
1
2
2
sec
3
4
p
x
r
1
2
2
cot
3
4
p
x
y
1
1
1. ■
PART II: Algebra and Identities
We begin by noting the relationship between the cotangent and tangent functions.
1
2
1
2
SECTION 6.6 Other Trigonometric Functions 499
Point-in-the-Plane
Description
Let t be a real number and (x, y) any point (except the origin) on the termi-
nal side of an angle of t radians in standard position. Let
r
x
2
y
2
.
Then,
cot t
x
y
, sec t
x
r
, csc t
y
r
for each number t in the domain of the given function.
3π
(−1, 1)
4
x
y
Figure 6–83
Reciprocal
Identities
The cotangent and tangent functions are reciprocals; that is,
cot t
ta
1
n t
and tan t
co
1
t t
for every number t in the domain of both functions.
The first of these identities was proved on page 497, and the second is proved sim-
ilarly (Exercise 49).

The proof of these statements uses the fact that each of these functions is the
reciprocal of a function whose period is known. For instance,
csc(t 2p)
sin(t
1
2p)
si
1
n t
csc t,
cot(t p)
tan(t
1
p)
ta
1
n t
cot t.
The other details are left as an exercise.
Proof By the definitions of the functions and the Pythagorean identity
(sin
2
t cos
2
t 1), we have
1 tan
2
t 1
c
s
o
in
s
2
2
t
t
cos
2
c
t
o
s
2
t
sin
2
t
co
1
s
2
t
co
1
s t
2
sec
2
t.
The second identity is proved similarly. ■
EXAMPLE 4
Simplify the expression
3
6
0
s
c
in
o
2
s
t
3
t
c
s
o
i
s
n
t
t
, assuming that sin t 0, cos t 0.
SOLUTION
3
6
0
s
c
in
o
2
s
t
3
t
c
s
o
i
s
n
t
t
5
c
c
o
o
s
s
t
3
t
si
s
n
in
2
t
t
5
s
c
in
os
t
2
t
5
c
s
o
in
s
t
t
cos t 5 cot t cos t. ■
EXAMPLE 5
Assume that cos t 0 and simplify cos
2
t cos
2
t tan
2
t.
500 CHAPTER 6 Trigonometric Functions
Period of Secant,
Cosecant, Cotangent
The secant and cosecant functions are periodic with period 2p and the
cotangent function is periodic with period p. In symbols,
sec(t 2p) sec t, csc(t 2p) csc t,
cot(t p) cot t
for every number t in the domain of the given function.
Pythagorean
Identities
For every number t in the domain of both functions,
1 tan
2
t sec
2
t
and
1 cot
2
t csc
2
t.
SOLUTION
cos
2
t cos
2
t tan
2
t cos
2
t(1 tan
2
t) cos
2
t sec
2
t cos
2
t
co
1
s
2
t
1. ■
EXAMPLE 6
If tan t 3/4 and sin t 0, find cot t, cos t, sin t, sec t, and csc t.
SOLUTION First we have cot t 1/tan t 1/(3/4) 4/3. Next we use the
Pythagorean identity to obtain
sec
2
t 1 tan
2
t 1
3
4
2
1
1
9
6
2
1
5
6
sec t
2
1
5
6
5
4
co
1
s t
5
4
or, equivalently, cos t
4
5
.
Since sin t is given as negative and tan t sin t/cos t is positive, cos t must be
negative. Hence, cos t 4/5. Consequently,
3
4
tan t
c
s
o
in
s
t
t
(
si
4
n
/
t
5)
so
sin t
4
5
3
4
3
5
.
Therefore,
sec t
co
1
s t
(4
1
/5)
5
4
and csc t
si
1
n t
(3
1
/5)
5
3
. ■
PART III: Graphs
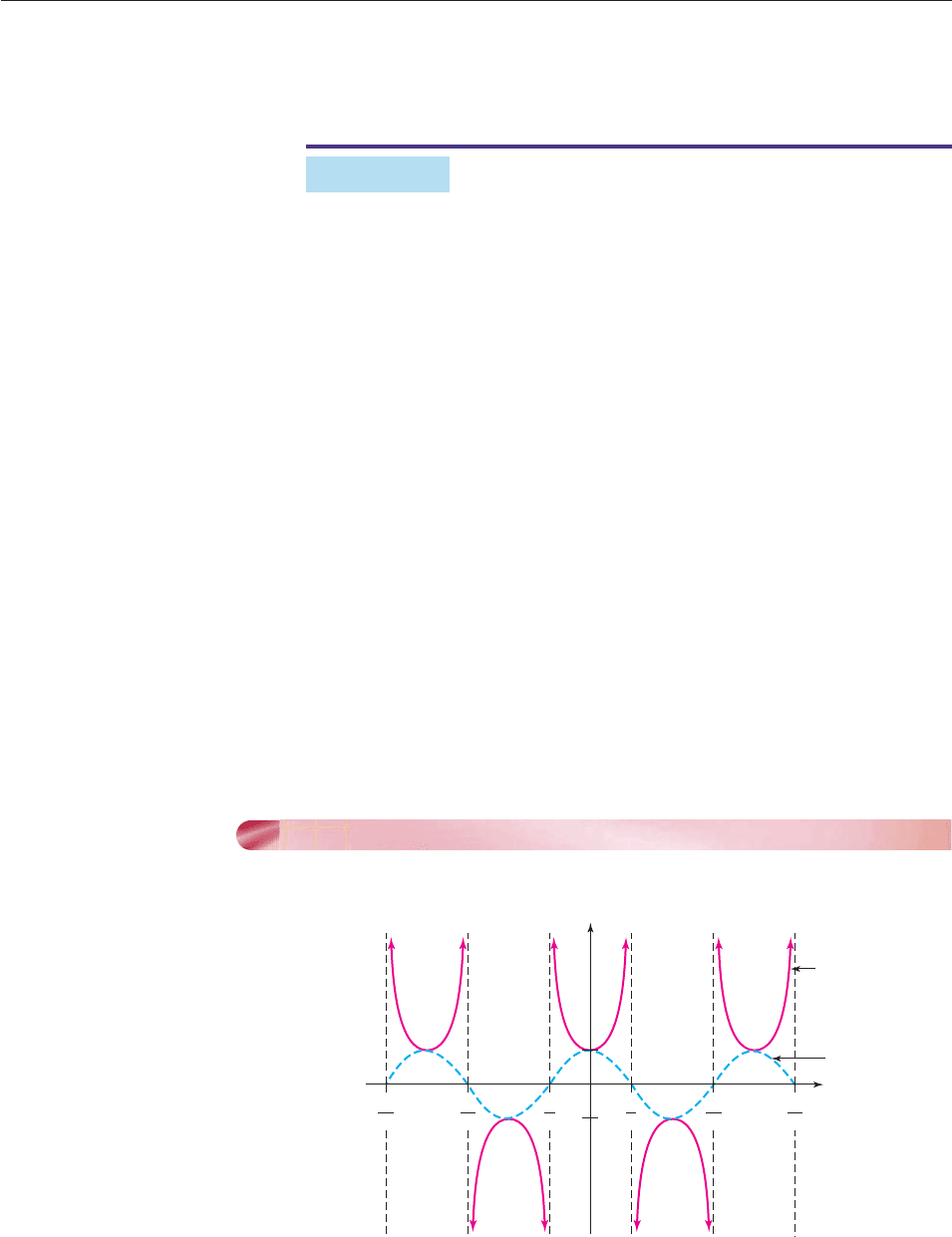
The graph of the secant function is shown in red in Figure 6–84.
Figure 6–84
g(t) = sec t
y = cos t
1
−1
π
2
−
t
y
π
2
3π
2
−
3π
2
5π
2
−
5π
2
SECTION 6.6 Other Trigonometric Functions 501
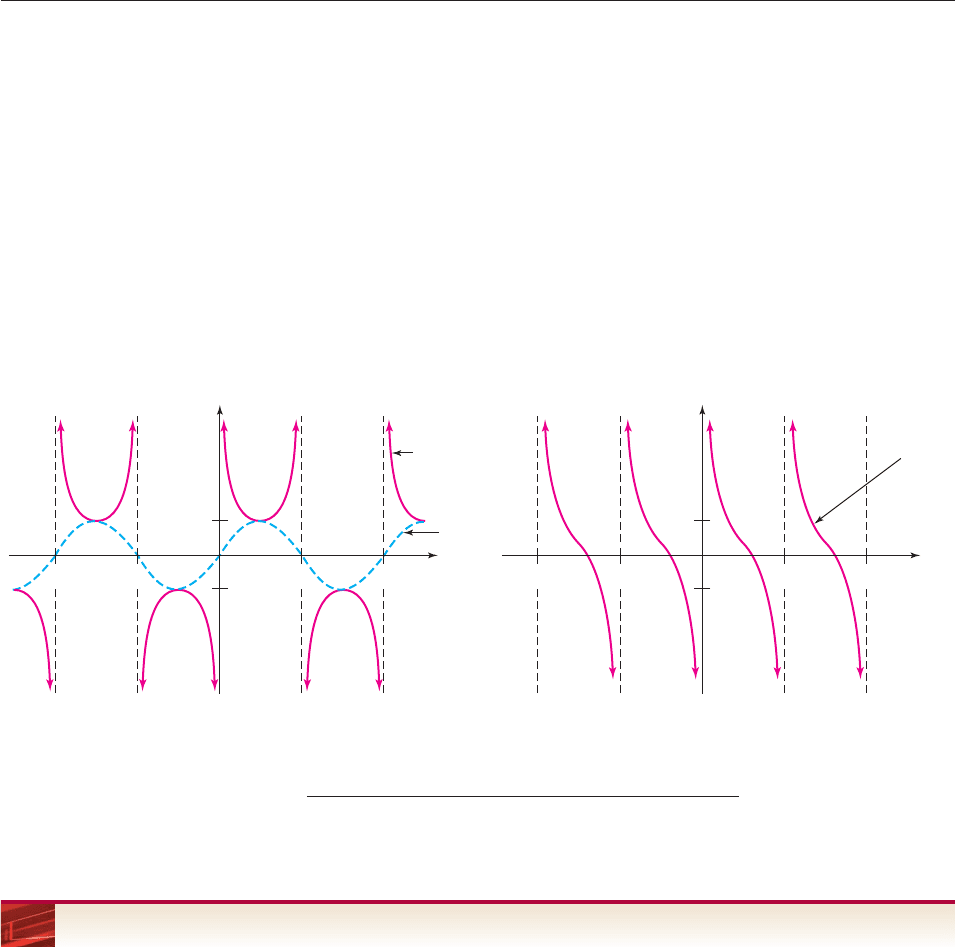
The shape of the secant graph can be understood by looking at the graph of cosine
(blue in Figure 6–84) and noting these facts:
1. sec t 1/cos t is not defined when cos t 0, that is, when t p/2,
3p/2, 5p/2, and so on.
2. The graph of sec t has a vertical asymptote at t p/2, 3p/2,
5p/2,...Thereason is that when cos t is close to 0 (graph close to
t-axis), then sec t 1/cos t is very large in absolute value,* so its graph
is far from the axis.
3. When cos t is near 1 or 1 (that is, when t is near 0, p, 2p,
3p, . . .), then so is sec t 1/cos t.
The graphs of h(t) csc t 1/sin t and f
(t) cot t 1/tan t can be
obtained in a similar fashion (Figure 6–85).
Figure 6–85
h(t) = csc t
1
−1
t
y
−π π−2π 2π
f(t) = cot t
1
−1
t
y
−π π−2π 2π
y = sin t
502 CHAPTER 6 Trigonometric Functions
*See the Big-Little Principle on page 288.
EXERCISES 6.6
Note: The arrangement of the exercises corresponds to the sub-
sections of this section.
Part I: Definitions and Descriptions
In Exercises 1–6, determine the quadrant containing the termi-
nal side of an angle of t radians in standard position under the
given conditions.
1. cos t 0 and sin t 0
2. sin t 0 and tan t 0
3. sec t 0 and cot t 0
4. csc t 0 and sec t 0
5. sec t 0 and cot t 0
6. sin t 0 and sec t 0
In Exercises 7–16, evaluate all six trigonometric functions at t,
where the given point lies on the terminal side of an angle of t
radians in standard position.
7. (3, 4) 8. (0, 6)
9. (5, 12) 10. (2, 3)
11. (1/5, 1) 12. (4/5, 3/5)
13. (2
, 3
) 14. (2 3
, 3
)
15. (1 2
, 3) 16. (1 3
, 1 3
)

SECTION 6.6 Other Trigonometric Functions 503
17. Suppose the batter in Example 1 hits a popup (the ball
leaves the bat at an angle of 1.4 radians). What is the maxi-
mum height of the ball?
Exercises 18–20 deal with the path of a projectile (such as a
baseball, a rocket, or an arrow). If the projectile is fired with
an initial velocity of v feet per second at angle of t radians and
its initial height is k feet, then the path of the projectile is
given by
y
v
1
2
6
sec
2
t
x
2
(tan t)x k.*
You can think of the projectile as being fired in the direction of
the x-axis from the point (0, k) on the y-axis.
18. (a) Find a viewing window that shows the path of a pro-
jectile that is fired from a 20-foot high platform at an
initial velocity of 120 feet per second at an angle
of .8 radians.
(b) What is the maximum height reached by the projectile?
(c) How far down range does the projectile hit the
ground?
19. Do Exercise 18 for a projectile that is fired from ground
level at an initial velocity of 80 feet per second at an angle
of .4 radians.
20. Do Exercise 18 for a projectile that is fired from a 40-foot
high platform at an initial velocity of 125 feet per second at
an angle of 1.2 radians.
In Exercises 21–25, evaluate all six trigonometric functions at
the given number without using a calculator.
21.
4
3
p
22.
7
6
p
23.
7
4
p
24.
11
3
p
25.
1
4
1p
26. Fill in the missing entries in the following table. Give exact
answers, not decimal approximations.
27. Find the average rate of change of f (t) cot t from t 1 to
t 3.
28. Find the average rate of change of g(t) csc t from t 2 to
t 3.
29. (a) Find the average rate of change of f (t) tan t from
t 2 to t 2 h, for each of these values of h: .01,
.001, .0001, and .00001.
(b) Compare your answers in part (a) with the number
(sec 2)
2
. What would you guess that the instantaneous
rate of change of f (t) tan t is at t 2?
Part II: Algebra and Identities
In Exercises 30–36, perform the indicated operations, then
simplify your answers by using appropriate definitions and
identities.
30. tan t (cos t csc t) 31. cos t sin t (csc t sec t)
32. (1 cot t)
2
33. (1 sec t)
2
34. (sin t csc t)
2
35. (cot t tan t)(cot
2
t 1 tan
2
t)
36. (sin t csc t)(sin
2
t csc
2
t 1)
In Exercises 37–42, factor and simplify the given expression.
37. sec t csc t csc
2
t 38. tan
2
t cot
2
t
39. tan
4
t sec
4
t 40. 4 sec
2
t 8 sec t 4
41. cos
3
t sec
3
t 42. csc
4
t 4 csc
2
t 5
In Exercises 43–48, simplify the given expression. Assume that
all denominators are nonzero and all quantities under radicals
are nonnegative.
43.
c
si
o
n
s
2
2
t
t
c
s
o
in
s
t
t
44.
sec
2
t
s
2
ec
se
t
c t 1
45. 46.
s
c
e
s
c
c
2
2
t
t
c
se
sc
c
t
t
47. (2 tan t
)(2 tan t
)
4 tan t sec t 2 sec t
6 sin t sec t 2 sec t
t 0
p
6
p
4
p
3
p
2
2
3
p
3
4
p
5
6
p
p
3
2
p
sin t
cos t
tan t ——
cot t ——
sec t ——
csc t ——
*Wind resistance is ignored in this equation.
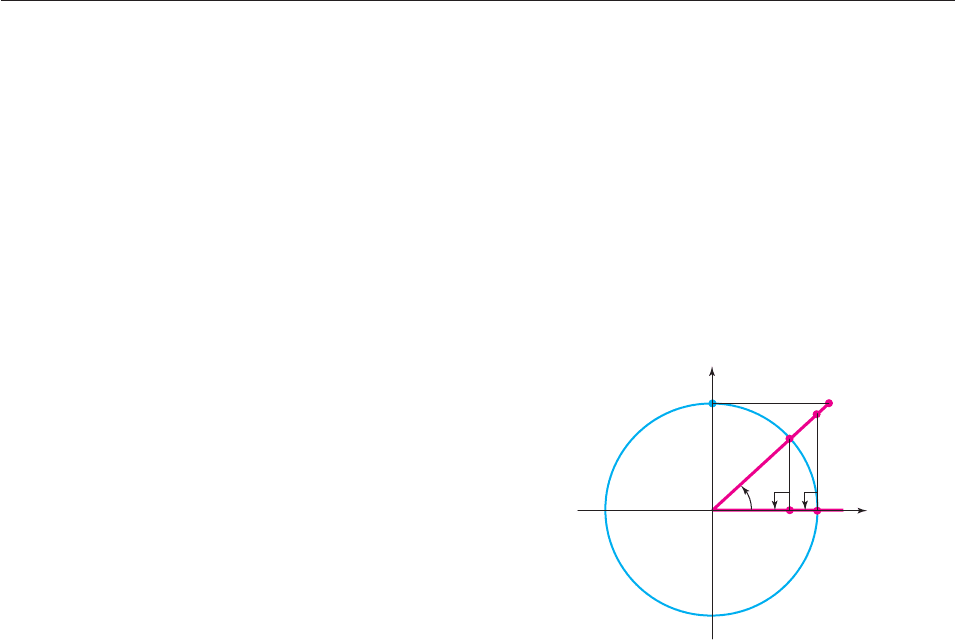
504 CHAPTER 6 Trigonometric Functions
48.
In Exercises 49–54, prove the given identity.
49. tan t
co
1
t t
[Hint: See page 497.]
50. sec(t 2p) sec t [Hint: See page 500.]
51. 1 cot
2
t csc
2
t [Hint: Look at the proof of the similar
identity on page 500]
52. cot(t) cot t [Hint: Express the left side in terms of
sine and cosine; then use the negative angle identities and
express the result in terms of cotangent.]
53. sec(t) sec t [Adapt the hint for Exercise 52.]
54. csc(t) csc t
In Exercises 55–60, find the values of all six trigonometric
functions at t if the given conditions are true.
55. cos t 1/2 and sin t 0
[Hint: sin
2
t cos
2
t 1.]
56. cos t
1
2
and sin t 0
57. cos t 0 and sin t 1
58. sin t 2/3 and sec t 0
59. sec t 13/5 and tan t 0
60. csc t 8 and cos t 0
Part III: Graphs
In Exercises 61–64, use graphs to determine whether the equa-
tion could possibly be an identity or is definitely not an identity.
61. tan t cot
p
2
t
62.
cos(t
co
s
p
t
/2)
cot t
6 tan t sin t 3 sin t
9 sin
2
t 3 sin t
63.
1
sin
co
t
s t
cot t
64.
se
1
c
t
ta
c
n
sc
t
t
csc t
65. Show graphically that the equation sec t t has infinitely
many solutions, but none between p/2 and p/2.
THINKERS
66. In the diagram of the unit circle in the figure, find six line
segments whose respective lengths are sin t, cos t, tan t,
cot t, sec t, csc t. [Hint: sin t length CA. Why? Note that
OC has length 1 and various right triangles in the figure are
similar.]
67. In the figure for Exercise 66, find the following areas in
terms of u.
(a) triangle OCA
(b) triangle ODB
(c) circular segment OCB
θ
A
O
B = (1, 0)
F = (0, 1)
E
D
C
y

CHAPTER 6 Review 505
Chapter 6 Review
IMPORTANT CONCEPTS
Section 6.1
Angle 428
Vertex 428
Initial side 428
Terminal side 428
Coterminal angles 429
Standard position 429
Positive and negative angles 429
Degree measure 429
Radian measure 430
Special Topics 6.1.A
Arc length 435
Area of a sector 437
Linear speed 438–439
Angular speed 438–439
Section 6.2 [Alternate Section 6.2]
Sine function 442 [452, 455]
Cosine function 442 [452, 455]
Tangent function 443 [452, 455]
Special values 445 [456]
Point-in-the-plane description 447
[453]
Section 6.3
Algebra with trigonometric
functions 458
Pythagorean identity 460
Periodicity 462
Negative angle identities 463
Section 6.4
Graphs of sine, cosine, and tangent
functions 466–472
Graphs and identities 473
Section 6.5
Period 478
Amplitude 480
Phase shift 482
Simple harmonic motion 485
Special Topics 6.5.A
Sinusoidal graphs 491
Damped and compressed graphs 493
Section 6.6
Cotangent function 497
Secant function 497
Cosecant function 497
Point-in-the-plane descriptions 499
Identities 499–500
Graphs of cotangent, secant, and
cosecant functions 501–502
IMPORTANT FACTS & FORMULAS
■
Conversion Rules: To convert radians to degrees, multiply by 180/p. To convert degrees to radians,
multiply by p/180.
■
Definition of Trigonometric Functions: If P is the point where the terminal side of an angle of t radians in
standard position meets the unit circle, then
sin t y-coordinate of P,
cos t x-coordinate of P,
tan t
c
s
o
in
s
t
t
, cot t
c
s
o
in
s
t
t
, sec t
co
1
s t
, csc t
si
1
n t
.
■
Point-in-the-Plane Description: If (x, y) is any point other than the origin on the terminal side of an angle
of t radians in standard position and r
x
2
y
2
, then
sin t
y
r
, cos t
x
r
,
tan t
y
x
, cot t
x
y
,
sec t
x
r
, csc t
y
r
.
