Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

6.4 Basic Graphs
■ Analyze the graphs of the sine, cosine, and tangent functions.
■ Derive the graphs of other trigonometric functions from the
graphs of sine, cosine, and tangent.
■ Explore trigonometric identities graphically.
Although a graphing calculator will quickly sketch the graphs of the sine, cosine,
and tangent functions, it will not give you much insight into why these graphs
have the shapes they do and why these shapes are important. So the emphasis
here is on the connection between the definition of these functions and their
graphs.
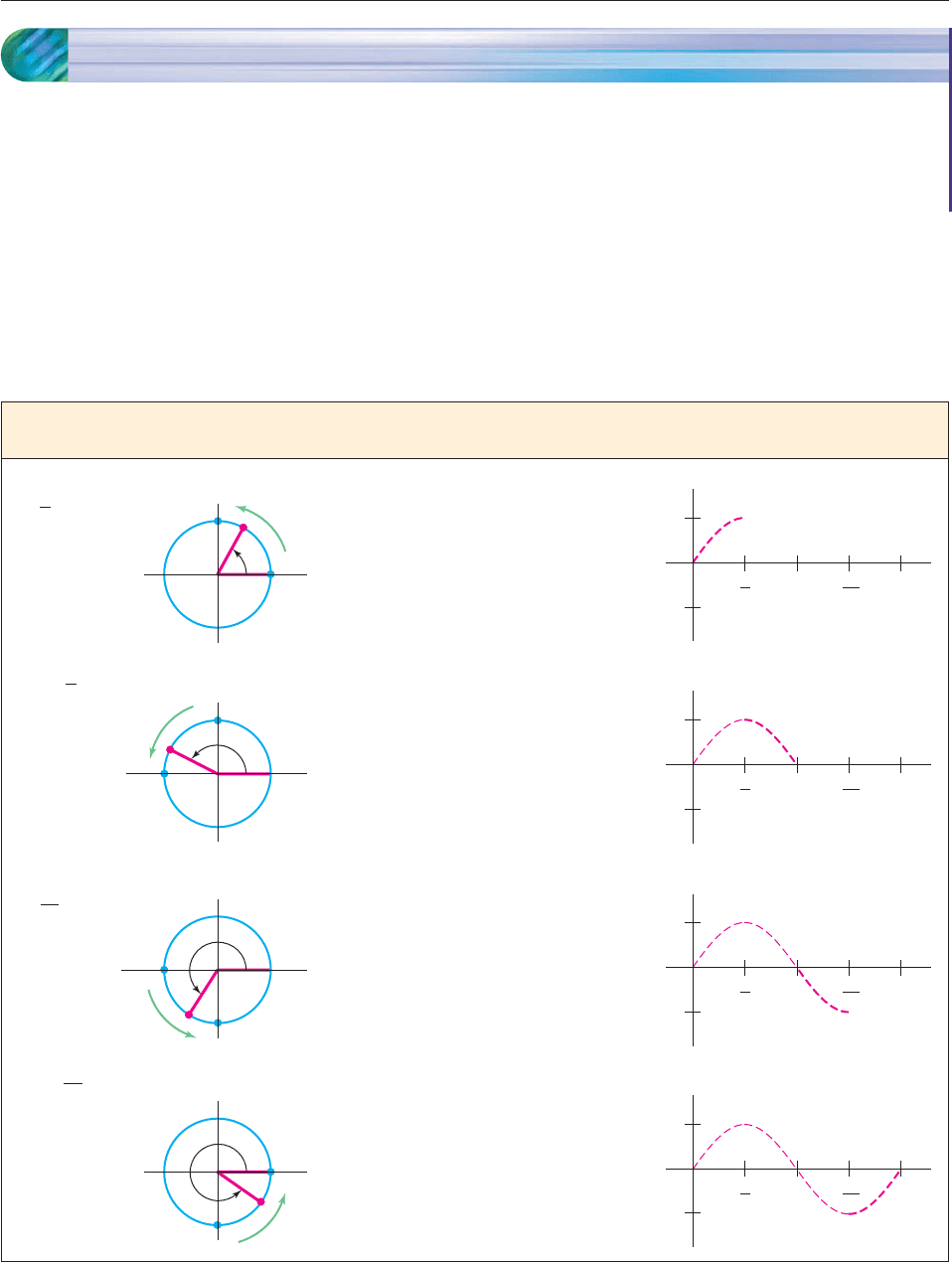
As t The y-coordinate Rough Sketch
Increases The Point P Moves of P( sin t) of the Graph
3π
2
1
from 0
to
π
2
from (1, 0) to (0, 1)
(1, 0)
(0, 1)
P
t
t
t
t
increases from 0
to 1
−1
ππ 2π
2
3π
2
1
−1
ππ 2π
2
3π
2
1
−1
ππ 2π
2
3π
2
1
−1
ππ 2π
2
from
to π
from (0, 1) to (−1, 0)
(−1, 0)
(−1, 0)
(0, 1)
decreases from 1
to 0
from π
to
from (−1, 0) to (0, −1)
(0, −1)
(0, −1)
decreases from 0
to −1
from
to 2π
from (0, −1) to (1, 0)
(1, 0)
increases from −1
to 0
P
P
P
π
2
3π
2
3π
2
Section Objectives
466 CHAPTER 6 Trigonometric Functions
If P is the point where the unit circle meets the terminal side of an angle of t
radians, then the y-coordinate of P is the number sin t. As shown in the chart on
the facing page, we can get a rough sketch of the graph of f (t) sin t by watch-
ing the y-coordinate of P.
SECTION 6.4 Basic Graphs 467
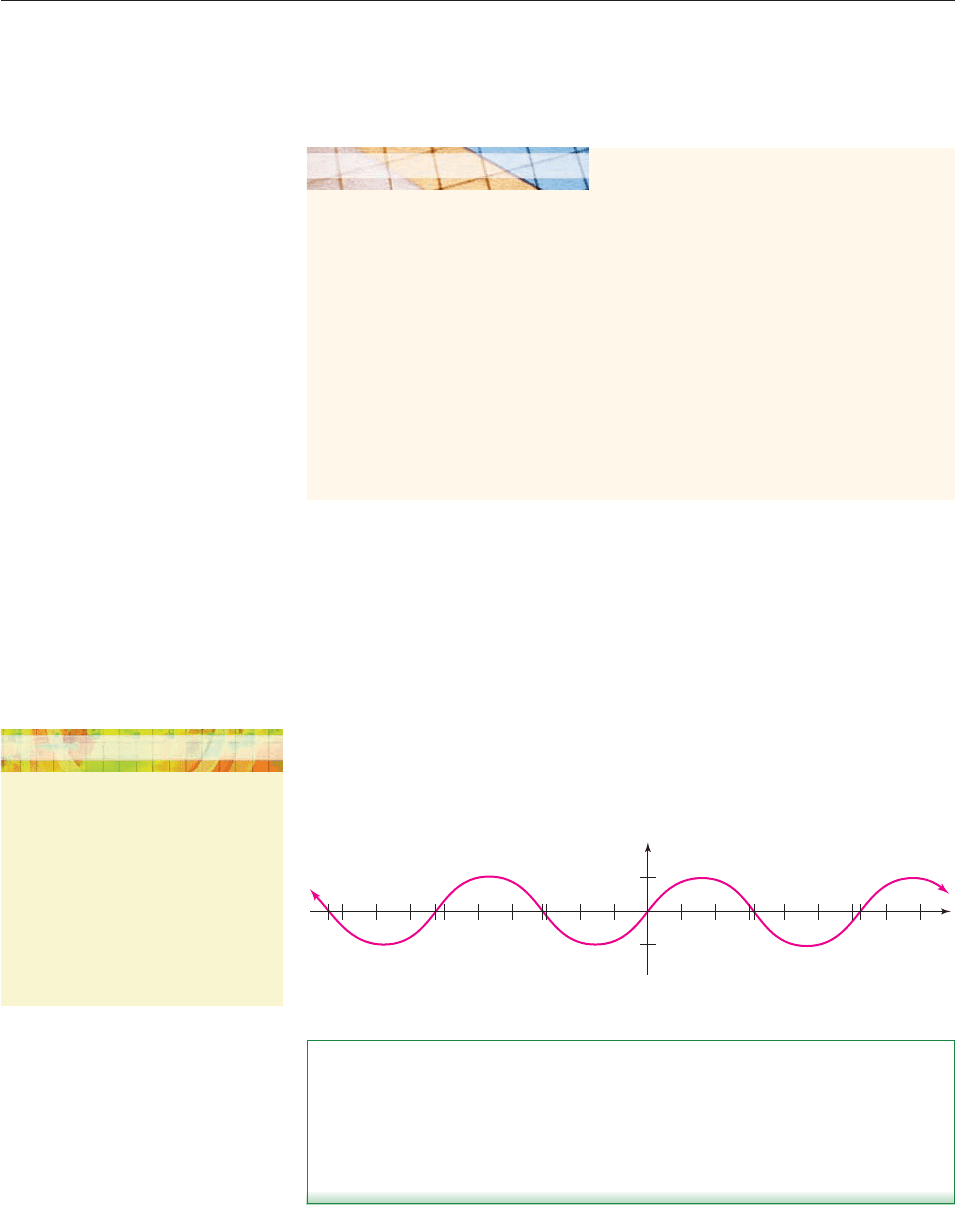
To complete the graph of the sine function, note that as t goes from 2p to 4p, the
point P on the unit circle retraces the path it took from 0 to 2p, so the same wave
shape will repeat on the graph. The same thing happens when t goes from 4p to
6p, or from 2p to 0, and so on. This repetition of the same pattern is simply the
graphical expression of the fact that the sine function has period 2p: For any num-
ber t, the points
(t, sin t) and (t 2p, sin(t 2p))
on the graph have the same second coordinate.
A graphing calculator or some point plotting with an ordinary calculator now
produces the graph of f (t) sin t (Figure 6– 44).
Figure 6–44
The graph of the sine function and the techniques of Section 3.4 can be used
to graph other trigonometric functions.
f(t) = sin t
1 π 2π
1
−1
−1−π−2π
t
y
Your calculator can provide a dynamic simulation of this process. Put it in paramet-
ric graphing mode and set the range values as follows:
0 t 6.28 1 x 6.28 2.5 y 2.5.
On the same screen, graph the two functions given by
x
1
cos t, y
1
sin t and x
2
t, y
2
sin t.
Using the trace feature, move the cursor along the first graph (the unit circle). Stop
at a point on the circle, and note the value of t and the y-coordinate of the point.
Then switch the trace to the second graph (the sine function) by using the up or
down cursor arrows. The value of t remains the same. What are the x- and y-coordinates
of the new point? How does the y-coordinate of the new point compare with the
y-coordinate of the original point on the unit circle?
GRAPHING EXPLORATION
NOTE
Throughout this chapter, we use t as the variable for trigonometric functions to avoid any confu-
sion with the x ’s and y’s that are part of the definition of these functions. For cal-
culator graphing in “function mode,” however, you must use x as the variable: f (x) sin x,
g(x) cos x, etc.
TECHNOLOGY TIP
Calculators have built-in windows for
trigonometric functions, in which the
x-axis tick marks are at intervals of
p/2.
Choose TRIG or ZTRIG in this menu:
TI: ZOOM
HP-39gs: VIEWS
Casio: V-WINDOW
EXAMPLE 1
The graph of h(t) 3 sin t is the graph of f (t) sin t stretched away from the
horizontal axis by a factor of 3, as shown in Figure 6–45. ■
Figure 6–45
EXAMPLE 2
The graph of k(t)
1
2
sin t is the graph of f (t) sin t shrunk by a factor of 1/2
toward the horizontal axis and then reflected in the horizontal axis, as shown in
Figure 6–46. ■
Figure 6–46
GRAPH OF THE COSINE FUNCTION
To obtain the graph of g(t) cos t, we follow the same procedure as with sine,
except that we now watch the x-coordinate of P (which is cos t).
f(t) = sin t
k(t) =− sin t
1
2
π 2π
1
−1
−π−2π
t
y
f(t) = sin t
h(t) = 3 sin t
π 2π
1
3
−1
−3
−π−2π
y
468 CHAPTER 6 Trigonometric Functions
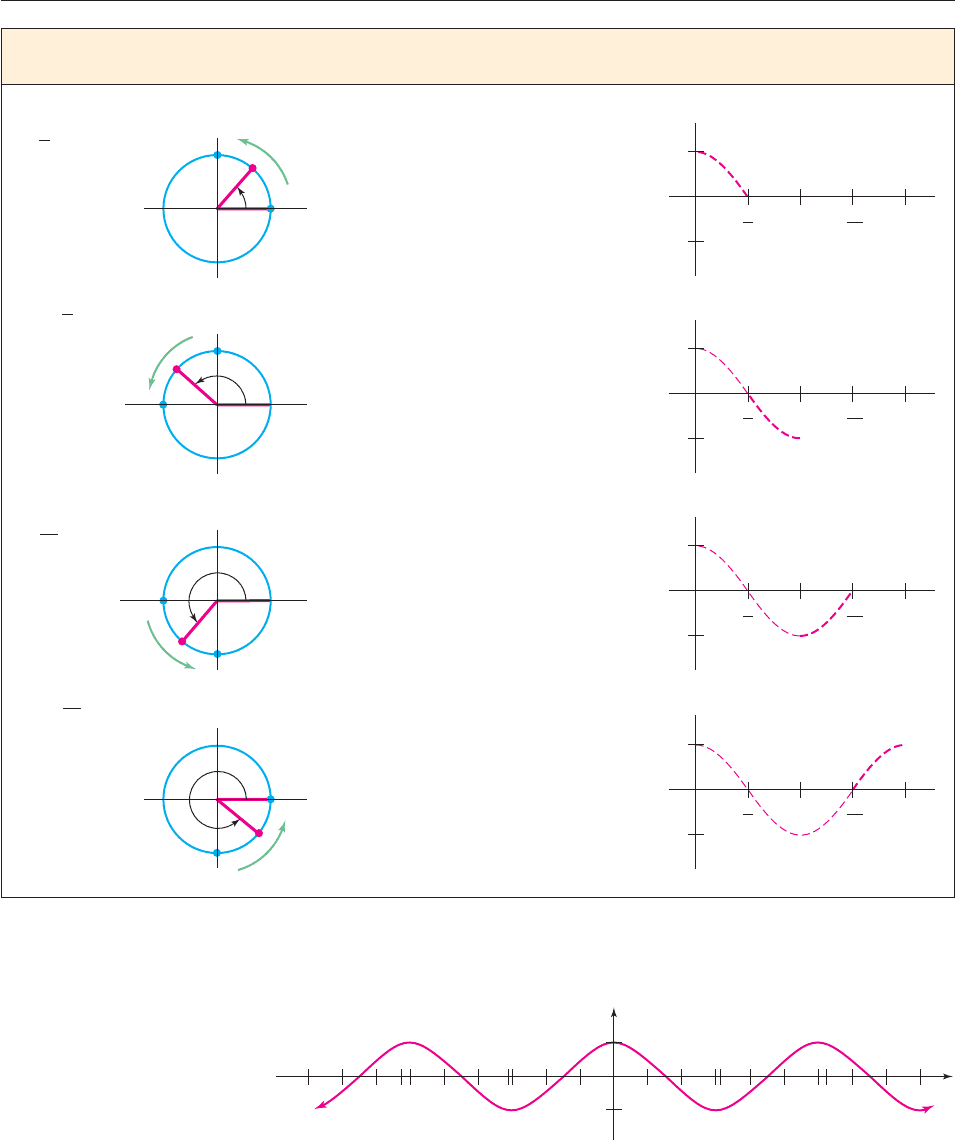
As t The x-coordinate Rough Sketch
Increases The Point P Moves of P ( cos t) of the Graph
As t takes larger values, P begins to retrace its path around the unit circle, so
the graph of g(t) cos t repeats the same wave pattern, and similarly for negative
values of t. So the graph looks like Figure 6– 47.
Figure 6– 47
For a dynamic simulation of the cosine graphing process described above, see
Exercise 69.
The techniques of Section 3.4 can be used to graph variations of the cosine
function.
g(t) = cos t
1 π 2π
1
−1
−1−π−2π
t
y
3π
2
1
from 0
to
from (1, 0) to (0, 1)
(1, 0)
(0, 1)
P
t
t
t
t
decreases from 1
to 0
−1
ππ 2π
2
3π
2
1
−1
ππ 2π
2
3π
2
1
−1
ππ 2π
2
3π
2
1
−1
ππ 2π
2
from
to π
from (0, 1) to (−1, 0)
(−1, 0)
(−1, 0)
(0, 1)
decreases from 0
to −1
from π
to
from (−1, 0) to (0, −1)
(0, −1)
(0, −1)
increases from −1
to 0
from
to 2π
from (0, −1) to (1, 0)
(1, 0)
increases from 0
to 1
P
P
P
3π
2
3π
2
π
2
π
2
SECTION 6.4 Basic Graphs 469
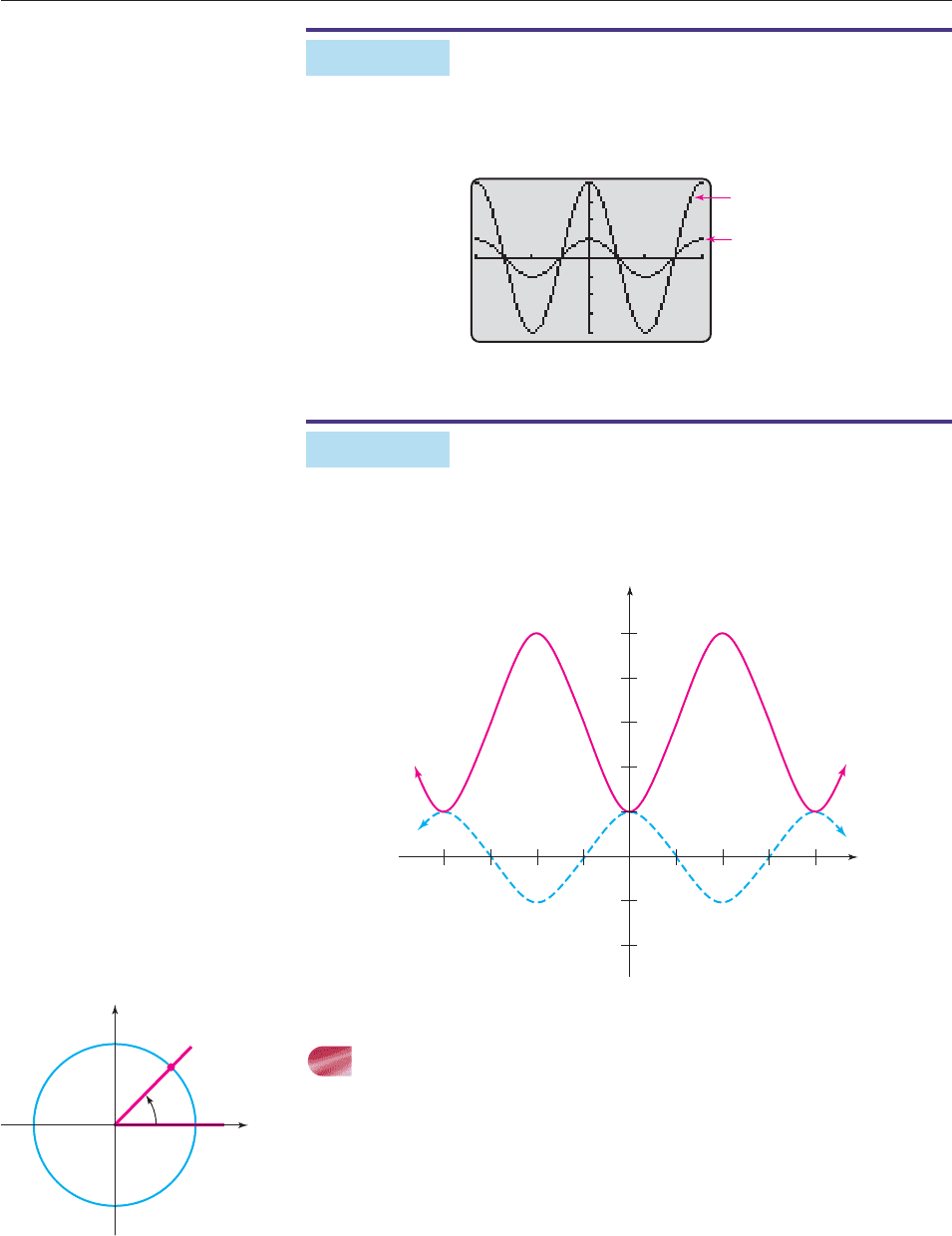
EXAMPLE 3
The graph of h(t) 4 cos t is the graph of g(t) cos t stretched away from the
horizontal axis by a factor of 4, as shown in Figure 6– 48. ■
Figure 6– 48
EXAMPLE 4
The graph of k(t) 2 cos t 3 is the graph of g(t) cos t stretched away from
the horizontal axis by a factor of 2, reflected in the horizontal axis, and shifted
vertically 3 units upward as shown in Figure 6– 49. ■
Figure 6– 49
GRAPH OF THE TANGENT FUNCTION
To determine the shape of the graph of h(t) tan t, we use an interesting connec-
tion between the tangent function and straight lines. As shown in Figure 6–50, the
point P where the terminal side of an angle of t radians in standard position meets
the unit circle has coordinates (cos t, sin t). We can use this point and the
point (0, 0) to compute the slope of the terminal side.
slope
c
s
o
in
s
t
t
0
0
c
s
o
in
s
t
t
tan t
g(t) = cos t
k(t) =−2 cos t + 3
π 2π
1
2
3
4
5
−1
−π−2π
t
y
g(t) = cos t
h(t) = 4 cos t
−4
−2π 2π
4
470 CHAPTER 6 Trigonometric Functions
1
−1
−1
1
(cos t, sin t)
x
P
t
y
Figure 6–50
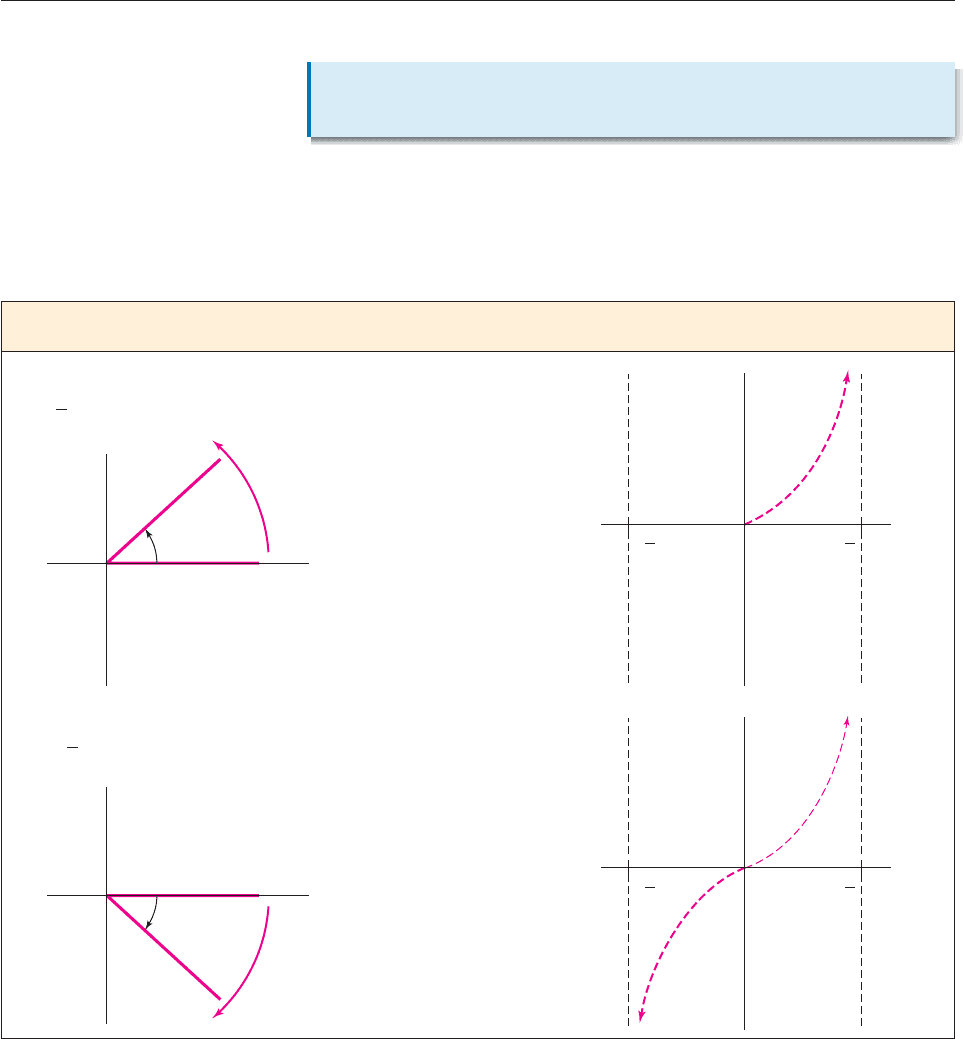
Therefore, we have the following.
The graph of h(t) tan t can now be sketched by watching the slope of the
terminal side of an angle of t radians, as t takes different values. Recall that the
more steeply a line rises from left to right, the larger its slope. Similarly, lines that
fall from left to right have negative slopes that increase in absolute value as the
line falls more steeply.
As t The Terminal Side Rough Sketch
Changes of the Angle Moves Its Slope (tan t) of the Graph
When t p/2, the terminal side of the angle is vertical, and hence its slope is
not defined. This corresponds to the fact that the tangent function is not defined
when t p/2. The vertical lines through p/2 are vertical asymptotes of the
graph: It gets closer and closer to these lines but never touches them.
As t goes from p/2 to 3p/2, the terminal side goes from almost vertical with
negative slope to horizontal to almost vertical with positive slope (draw a picture),
exactly as it does between p/2 and p/2. So the graph repeats the same pattern.
The same thing happens between 3p/2 and 5p/2, between 3p/2 and p/2, etc.
Therefore, the entire graph looks like Figure 6–51 on the next page.
from 0
to
from horizontal upward
toward vertical
increases from 0
in the positive
direction and
keeps getting
larger
π
2
π
−
2
from 0
to −
from horizontal downward
toward vertical
decreases from 0
in the negative
direction and
keeps getting
larger in absolute
value
π
2
π
−
2
t
t
π
2
π
2
SECTION 6.4 Basic Graphs 471
Slope and
Tangent
The slope of the terminal side of an angle of t radians in standard position
is the number tan t.
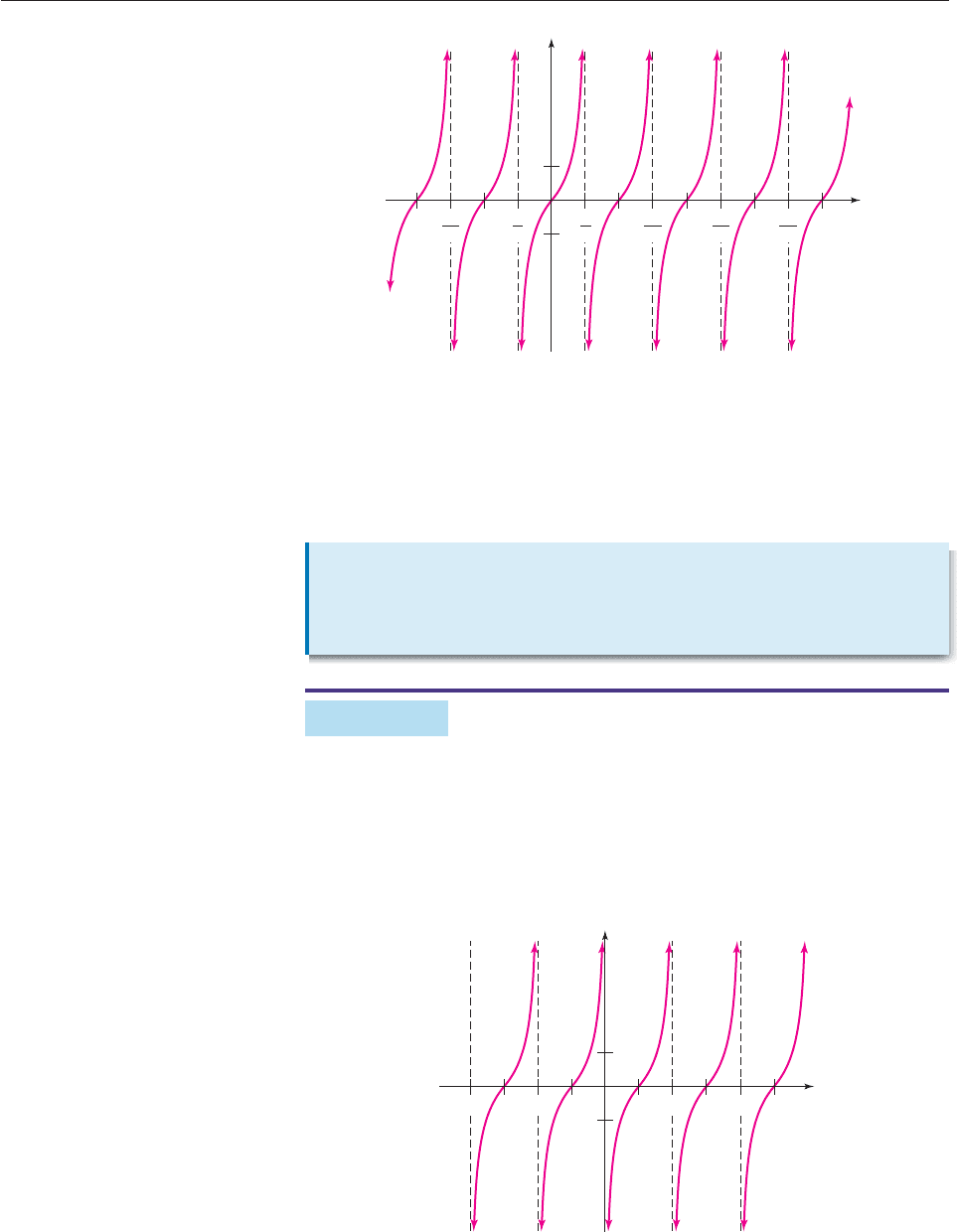
Figure 6–51
Because calculators sometimes do not graph accurately across vertical asymp-
totes, the graph may look slightly different on a calculator screen (with vertical line
segments where the asymptotes should be).
The graph of the tangent function repeats the same pattern at intervals of
length p. This means that the tangent function repeats its values at intervals of p.
EXAMPLE 5
As we saw in Section 3.4, the graph of
k(t) tan
t
p
2
is the graph of h(t) tan t shifted horizontally p/2 units to the right (Fig-
ure 6–52). ■
Figure 6–52
π
1
−1
−π
t
y
0
2π−2π
h(t) = tan t
π
2
π
3π 4π
1
−1
−−
−π
t
y
π
2
3π
2
0
2π−2π
3π
2
5π
2
7π
2
472 CHAPTER 6 Trigonometric Functions
Period of
Tangent
The tangent function is periodic with period p: For every real number t in
its domain,
tan(t p) tan t.
GRAPHS AND IDENTITIES
Graphing calculators can be used to identify equations that could possibly be
identities. A calculator cannot prove that such an equation is an identity; but it can
provide evidence that it might be one. On the other hand, a calculator can prove
that a particular equation is not an identity.
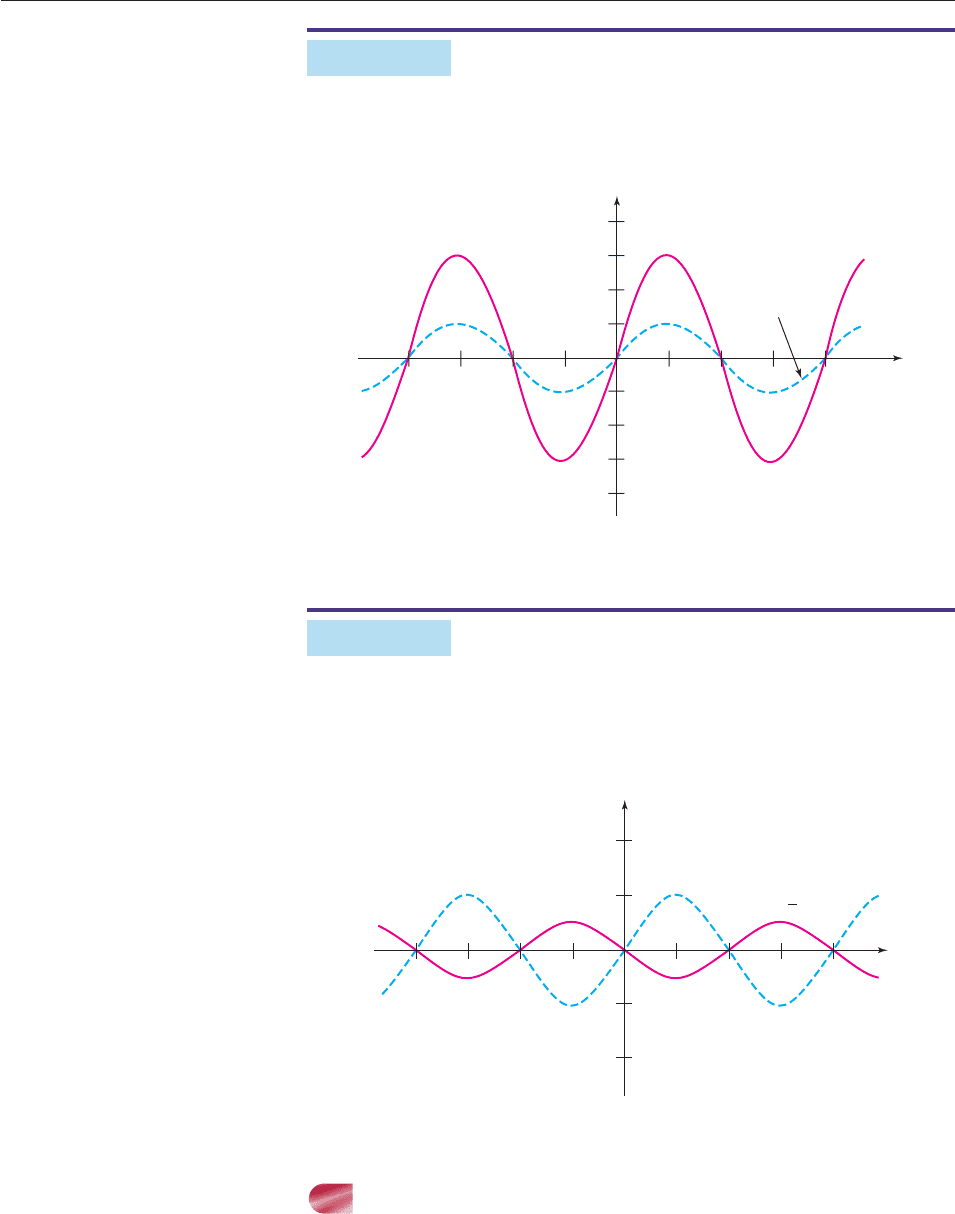
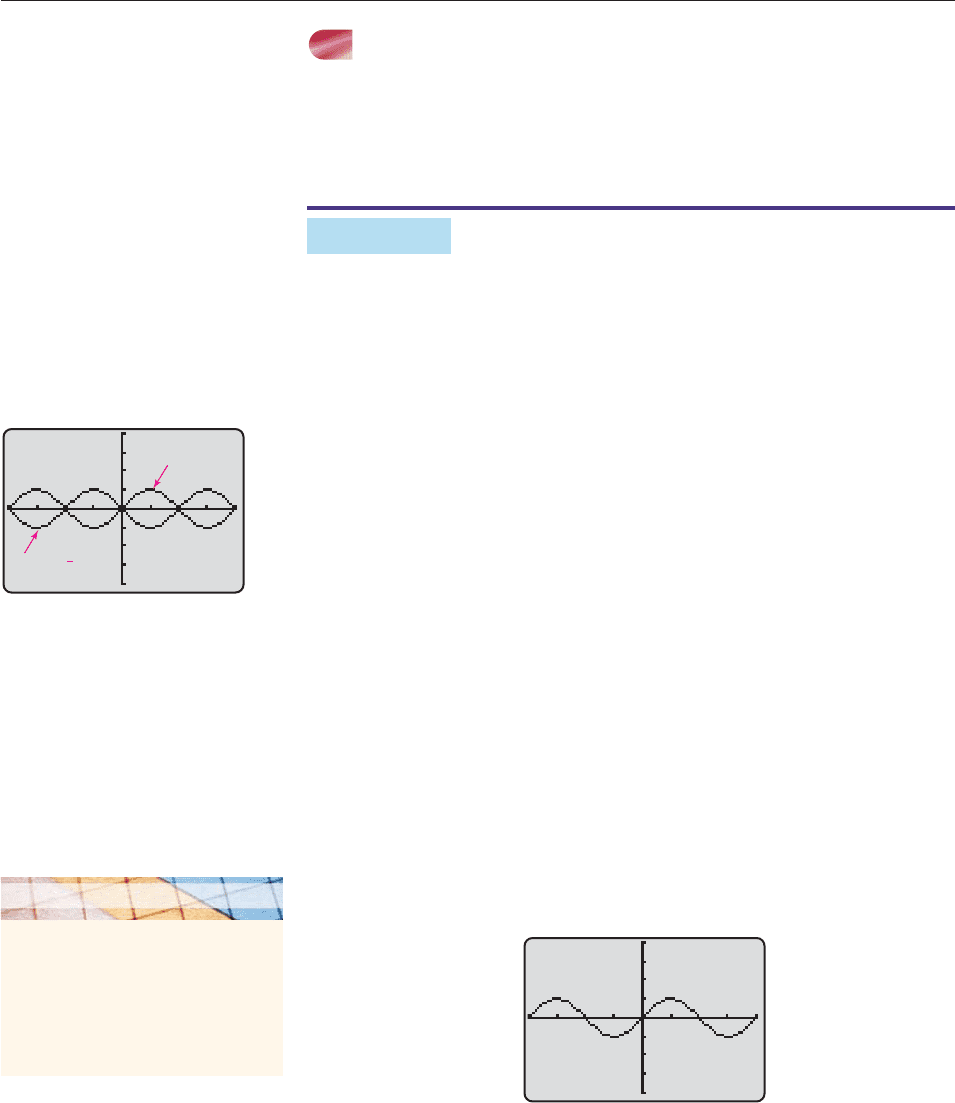
EXAMPLE 6
Which of the following equations could possibly be an identity?
(a) cos
p
2
t
sin t (b) cos
p
2
t
sin t
SOLUTION
(a) Consider the functions f (t) cos
p
2
t
and g(t) sin t, whose rules are
given by the two sides of the equation
cos
p
2
t
sin t.
If this equation is an identity, then f(t) g(t) for every real number t, and
hence, f and g have the same graph. But the graphs of f and g on the interval
[2p, 2p] (Figure 6–53) are obviously different. Therefore, this equation is
not an identity.
(b) We can test this equation in the same manner. The graph of the left side, that
is, the graph of
h(t) cos
p
2
t
,
in Figure 6–54 appears to be the same as the graph of g(t) sin t on the inter-
val [2p, 2p] (Figure 6–53). To check this, do the Graphing Exploration in
the margin.
SECTION 6.4 Basic Graphs 473
g(t) = sin t
f(t) = cos + t
()
π
2
−4
4
Figure 6–53
−4
4
Figure 6–54
The fact that the graphs appear to be identical means that the two functions have
the same value at every number t that the calculator computed in making the
graphs (at least 95 numbers). This evidence strongly suggests that the equation
GRAPHING EXPLORATION
Graph h(t) cos
p
2
t
and
g(t) sin t on the same screen
and use the trace feature to con-
firm that the graphs appear to be
identical.

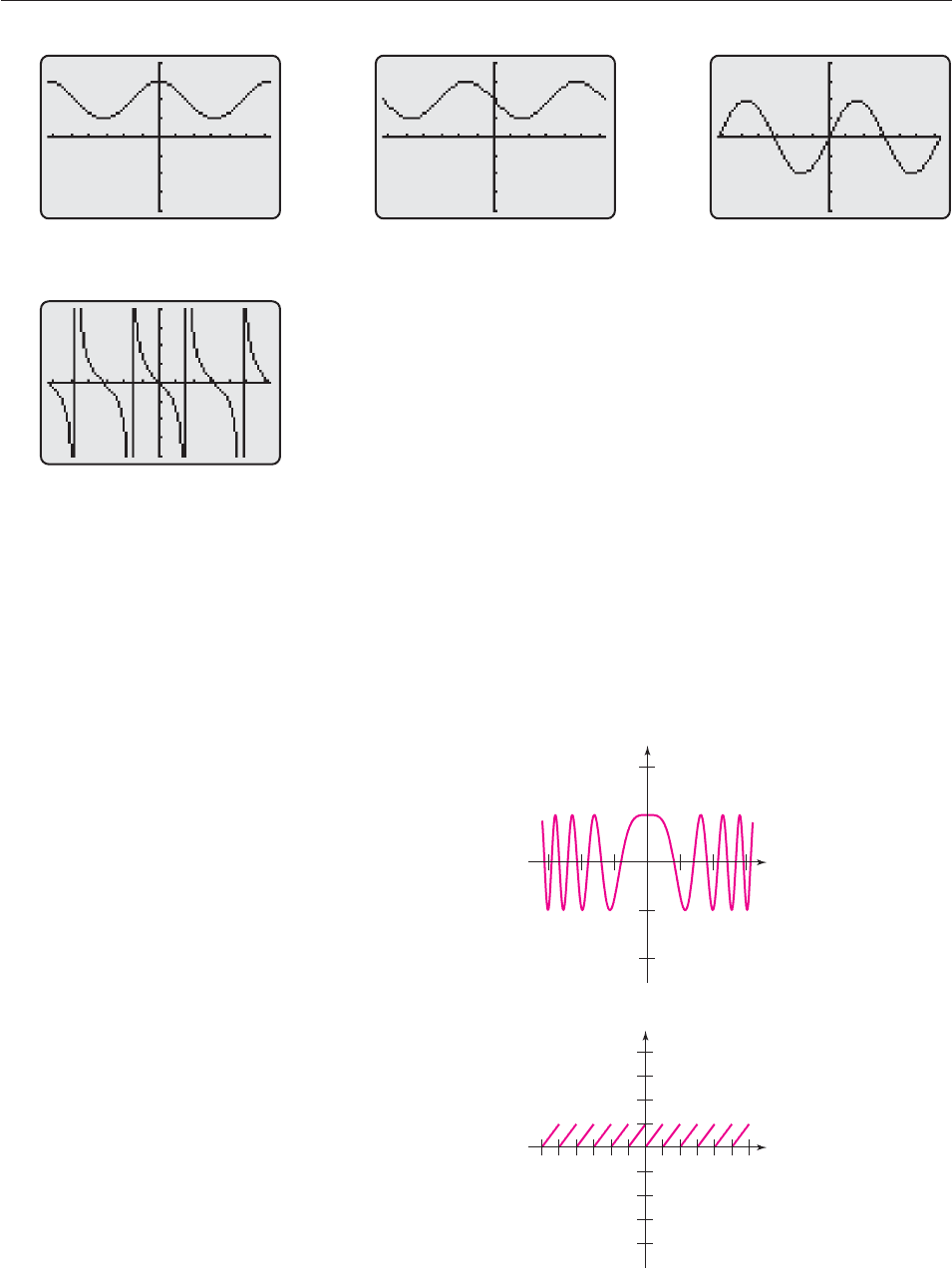
In Exercises 23–30 match the function with its graph, which is one of A–J below. [Note: the tangent graphs have erroneous vertical
lines where the vertical asymptotes should be.]
23. f(t) 4 sin t 24. g(t) tan t 25. h(t) 3 tan t 26. k(t) 2 sin t
27. f(t) 2 cos t 28. g(t) 2 sin t 29. h(t) cos t 2 30. k(t) 2 2 sin t
474 CHAPTER 6 Trigonometric Functions
EXERCISES 6.4
In Exercises 1–6, use the graphs of the sine and cosine func-
tions to find all the solutions of the equation.
1. sin t 0 2. cos t 0 3. sin t 1
4. sin t 1 5. cos t 1 6. cos t 1
In Exercises 7–10, find tan t, where the terminal side of an
angle of t radians lies on the given line.
7. y 11x 8. y 1.5x 9. y 1.4x 10. y .32x
In Exercises 11–22, list the transformations needed to change
the graph of f(t) into the graph of g(t). [See Section 3.4.]
11. f(t) sin t; g(t) sin t 3
12. f(t) cos t; g(t) cos t 2
13. f(t) cos t; g(t) cos t
14. f(x) sin t; g(t) 3 sin t
15. f(t) tan t; g(t) tan t 5
16. f(t) tan t; g(t) tan t
17. f(t) cos t; g(t) 3 cos t
18. f(t) sin t; g(t) 2 sin t
19. f(t) sin t; g(t) 3 sin t 2
20. f(t) cos t; g(t) 5 cos t 3
21. f(t) sin t; g(t) sin(t 2)
22. f(t) cos t; g(t) 3 cos(t 2) 3
4
4
2 2
4
4
2 2
4
4
2 2
4
4
2 2
4
4
2 2
4
4
2 2
A. B. C.
D. E. F.
cos
p
2
t
sin t is an identity, but does not prove it. All we can say at this
point is that the equation possibly is an identity. ■
CAUTION
Do not assume that two graphs that look the same on a calculator screen actually are the same.
Depending on the viewing window, two graphs that are actually quite different may appear to be
identical. See Exercises 61, 62, and 64–67 for some examples.
SECTION 6.4 Basic Graphs 475
In Exercises 31–38, use the graphs of the trigonometric func-
tions to determine the number of solutions of the equation
between 0 and 2p.
31. sin t 3/5 [Hint: How many points on the graph of
f(t) sin t between t 0 and t 2p have second coor-
dinate 3/5?]
32. cos t 1/4 33. tan t 4
34. cos t 2/3 35. sin t 1/2
36. sin t k, where k is a nonzero constant such that
1 k 1.
37. cos t k, where k is a constant such that 1 k 1.
38. tan t k, where k is any constant.
In Exercises 39–50, use graphs to determine whether the
equation could possibly be an identity or definitely is not an
identity.
39. sin(t) sin t
40. cos(t) cos t
41. sin
2
t cos
2
t 1
42. sin(t p) sin t
43. sin t cos(t p/2)
44. sin
2
t tan
2
t (sin
2
t)(tan
2
t)
45.
1
sin
co
t
s t
tan t
46.
1
cos
si
t
n t
co
1
s t
tan t
47. cos
p
2
t
sin t
4
4
2 2
48. sin
p
2
t
cos t
49. (1 tan t)
2
co
1
s t
50. (cos
2
t 1)(tan
2
t 1) tan
2
t
In Exercises 51–54, determine if the graph appears to be the
graph of a periodic function. If it is, state the period.
51.
52.
246
2
4
−4
−2
−2−6 −4
t
y
π
2
1
−1
−2
−π
t
y
G. H. I.
4
4
2 2
4
4
2 2
4
4
2 2
J.
