Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

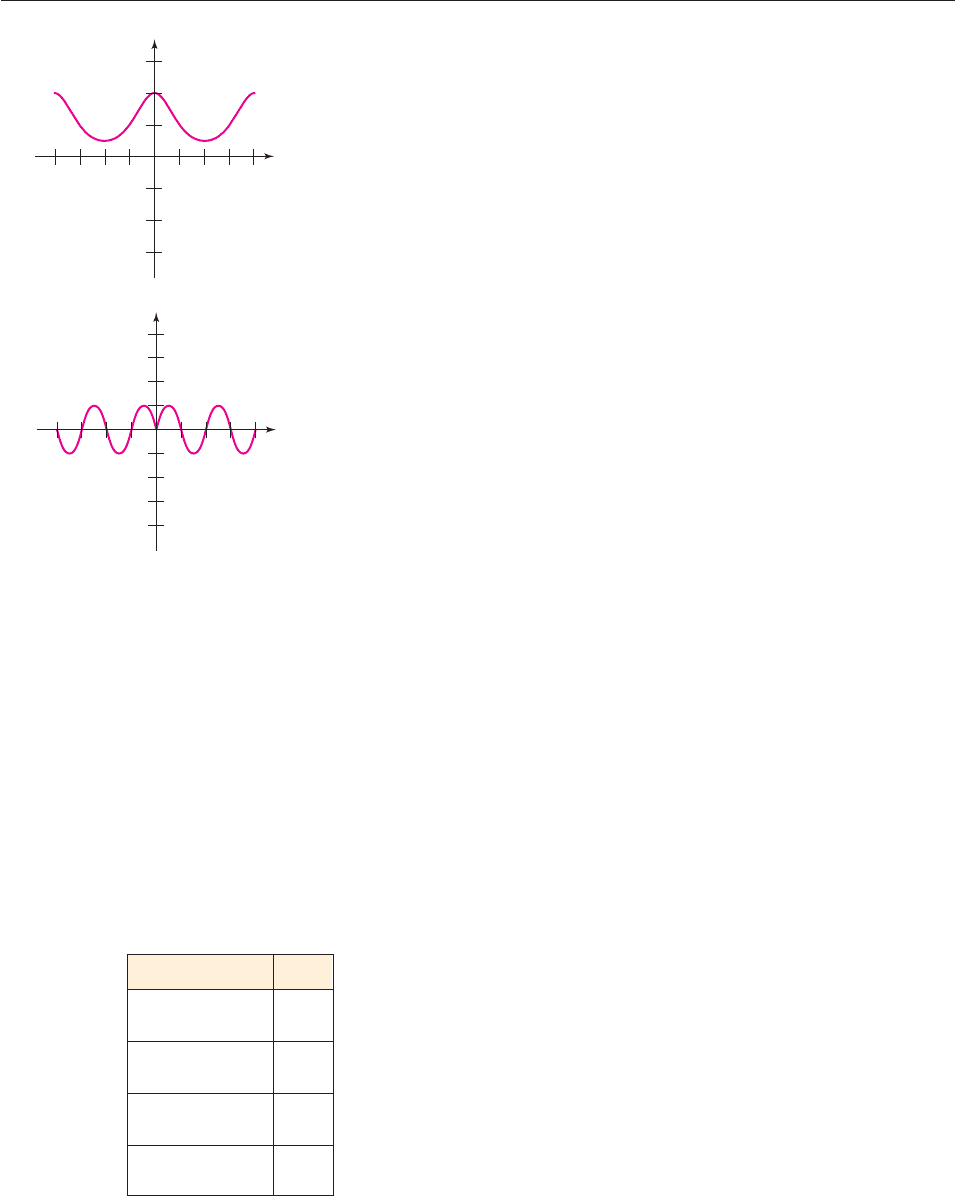
476 CHAPTER 6 Trigonometric Functions
53.
54.
In Exercises 55–60, graph the function. Does the function
appear to be periodic? If so, what is the period?
55. f(t) cos t 56. f(t) cos t
57. g(t) sin t 58. g(t) sin t
59. h(t) tan t 60. h(t) tan t
THINKERS
Exercises 61–64, explore various ways in which a calculator
can produce inaccurate graphs of trigonometric functions.
These exercises also provide examples of two functions, with
different graphs, whose graphs appear identical in certain
viewing windows.
61. Choose a viewing window with 3 y 3 and 0 x k,
where k is chosen as follows.
(a) Graph y cos x and the constant function y 1 on the
same screen. Do the graphs look identical? Are the
functions the same?
π
2π
1
2
3
4
−1
−2
−3
−4
−π−2π
t
y
π
2π
2
1
3
−1
−2
−3
−π−2π
t
y
(b) Use the trace feature to move the cursor along the graph
of y cos x, starting at x 0. For what values of x did
the calculator plot points? [Hint: 2p 6.28.] Use this
information to explain why the two graphs look
identical.
62. Using the viewing window in Exercise 61, graph
y tan x 2 and y 2 on the same screen. Explain why
the graphs look identical even though the functions are not
the same.
63. The graph of g(x) cos x is a series of repeated waves (see
Figure 6–47). A full wave (from the peak, down to the
trough, and up to the peak again) starts at x 0 and finishes
at x 2p.
(a) How many full waves will the graph make between
x 0 and x 502.65 ( 80
2p)?
(b) Graph g(t) cos t in a viewing window with
0 t 502.65. How many full waves are shown on
the graph? Is your answer the same as in part (a)?
What’s going on?
64. Find a viewing window in which the graphs of y cos x and
y .54 appear identical. [Hint: See the chart in Exercise 61
and note that cos 1 .54.]
Exercises 65–68 provide further examples of functions with
different graphs, whose graphs appear identical in certain
viewing windows.
65. Approximating trigonometric functions by polynomials. For
each odd positive integer n, let f
n
be the function whose
rule is
f
n
(t) t
3
t
3
!
5
t
5
!
7
t
7
!
n
t
n
!
.
Since the signs alternate, the sign of the last term might be
instead of , depending on what n is. Recall that n!
is the product of all integers from 1 to n; for instance,
5! 1
2
3
4
5 120.
(a) Graph f
7
(t) and g(t) sin t on the same screen in a
viewing window with 2p t 2p. For what
values of t does f
7
appear to be a good approximation
of g?
(b) What is the smallest value of n for which the graphs of
f
n
and g appear to coincide in this window? In this
case, determine how accurate the approximation is by
finding f
n
(2) and g(2).
66. For each even positive integer n, let f
n
be the function
whose rule is
f
n
(t) 1
2
t
2
!
4
t
4
!
6
t
6
!
8
t
8
!
n
t
n
!
.
(The sign of the last term may be instead of , depending
on what n is.)
(a) In a viewing window with 2p t 2p, graph f
6
,
f
10
, and f
12
.
Width of Screen k
95 pixels 188p
(TI-8384)
127 pixels 252p
(TI-86, Casio)
131 pixels 260p
(HP-39gs)
159 pixels 316p
(TI-89)

■ Identify the period, amplitude, and phase shift of the functions
f(t) A sin(bt c) and g(t) A cos(bt c)
■ Explore simple harmonic motion.
We now analyze functions whose rule is of the form
f (t) A sin(bt c)org(t) A cos(bt c),
where A, b, and c are constants. Many periodic phenomena can be modeled by
such functions, as we shall see below.
PERIOD
The functions f(t) sin t and g(t) cos t have period 2p, so each of their graphs
makes one full wave between 0 and 2p. The sine wave begins on the horizontal
axis, rises to height 1, falls to 1, and returns to the axis (Figure 6–55). The
cosine wave between 0 and 2p begins at height 1, falls to 1, and rises to height
1 again (Figure 6–56).
SECTION 6.5 Periodic Graphs and Simple Harmonic Motion 477
6.5 Periodic Graphs and Simple Harmonic Motion
Section Objectives
f(t) = sin t
−2
2
02π
2
g(t) = cos t
−2
2π
0
Figure 6–56
Figure 6–55
Graph the following functions, one at a time, in a viewing window with 0 t 2p.
Determine the number of complete waves in each graph and the period of the func-
tion (the length of one wave).
f (t) sin 2t, g(t) cos 3t, h(x) sin 4t, k(x) cos 5t.
GRAPHING EXPLORATION
(b) Find a value of n for which the graph of f
n
appears to
coincide (in this window) with the graph of a well-
known trigonometric function. What is the function?
67. Find a rational function whose graph appears to coincide
with the graph of h(t) tan t when
2p t 2p.
[Hint: Exercises 65 and 66.]
68. Find a periodic function whose graph consists of “square
waves.” [Hint: Consider the sum
sin pt
1
3
sin 3pt
1
5
sin 5pt
1
7
sin 7pt .]
69. With your calculator in parametric graphing mode and the
range values
0 t 6.28 1 x 6.28 2.5 y 2.5,
graph the following two functions on the same screen:
x
1
cos t, y
1
sin t and x
2
t, y
2
cos t.
Using the trace feature, move the cursor along the first
graph (the unit circle). Stop at a point on the circle, note the
value of t and the x-coordinate of the point. Then switch
the trace to the second graph (the cosine function) by using
the up or down cursor arrows. The value of t remains the
same. How does the y-coordinate of the new point compare
with the x-coordinate of the original point on the unit circle?
Explain what’s going on.
70. (a) Judging from their graphs, which of the functions
f (t) sin t, g(t) cos t, and h(t) tan t appear to be
even functions? Which appear to be odd functions?
(b) Confirm your answers in part (a) algebraically by using
appropriate identities from Section 6.3.
Although we arrived at this statement by generalizing from several graphs, it can
also be explained algebraically.
EXAMPLE 1
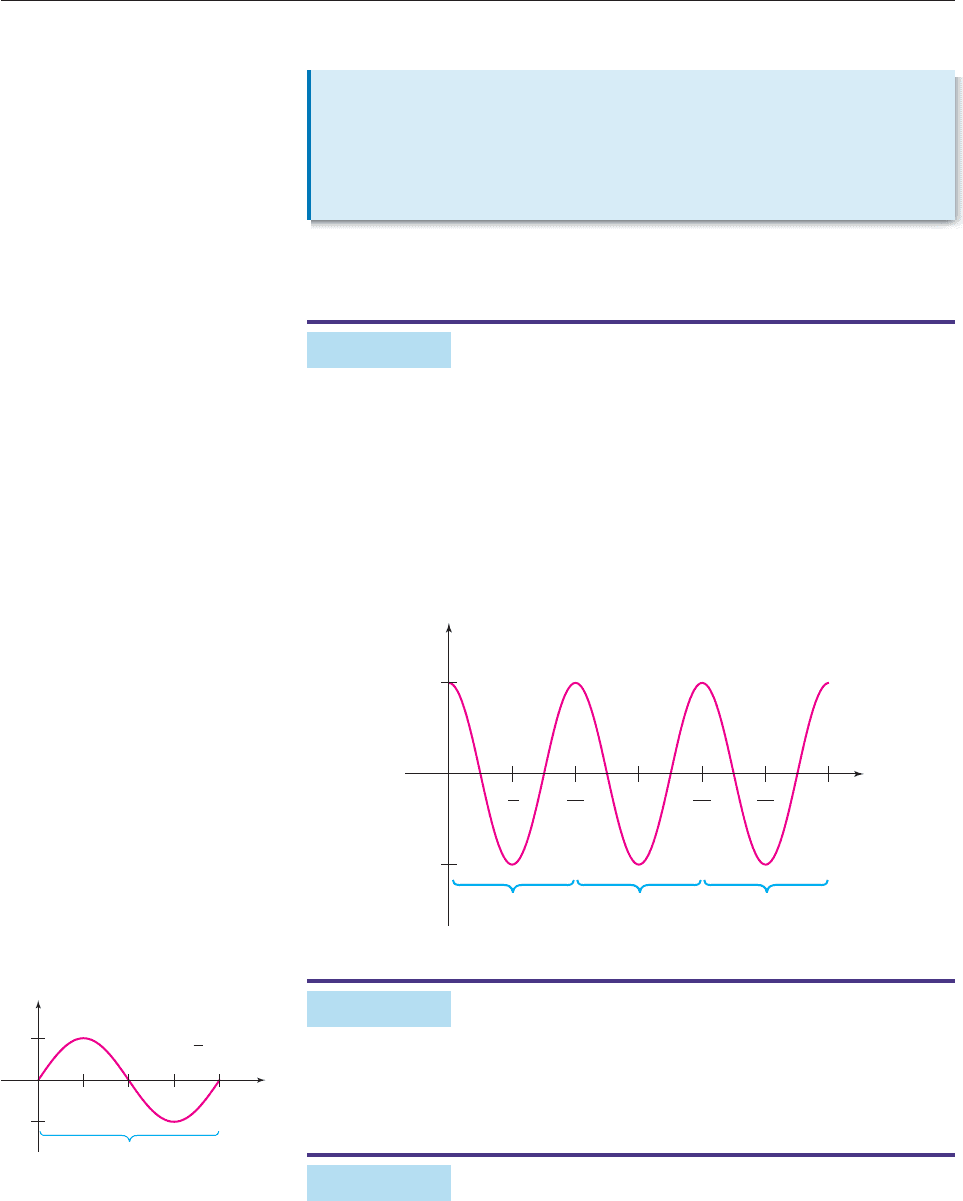
The graph of g(t) cos t makes one complete wave as t takes values from 0 to
2p. Similarly, the graph of k(t) cos 3t will complete one wave as the quantity
3t takes values from 0 to 2p. However,
3t 0 when t 0 and 3t 2p when t 2p/3.
So the graph of k(t) cos 3t makes one complete wave between t 0 and
t 2p/3, as shown in Figure 6–57, and hence k has period 2p/3. Similarly, the
graph makes a complete wave from t 2p/3 to t 4p/3 and another one from
t 4p/3 to t 2p, as shown in Figure 6–57. ■
478 CHAPTER 6 Trigonometric Functions
k(t) = cos 3t
π
3
π
1
−1
t
y
2π
1 wave 1 wave 1 wave
3
2π
5π
3
4π
3
Figure 6–57
EXAMPLE 2
According to the box above, the function f (t) sin
1
2
t has period
1
2
/
p
2
4p. Its graph
makes half a wave from t 0 to t 2p ( just as sin t does from t 0 to t p) and
the other half of the wave from t 2p to t 4p, as shown in Figure 6–58. ■
EXAMPLE 3
Except over very tiny intervals, your calculator is incapable of accurately graphing
f (t) sin bt or g(t) cos bt when b is large. For instance, we know that the graph of
f (t) sin 500t
f(t) = sin
π
1
−1
t
y
2π
t
2
1 wave
4π3π
Figure 6–58
Period
If b 0, then the graph of either
f(t) sin bt or g(t) cos bt
makes b complete waves between 0 and 2p. Hence, each function has
period 2p/b.
This exploration suggests the following.
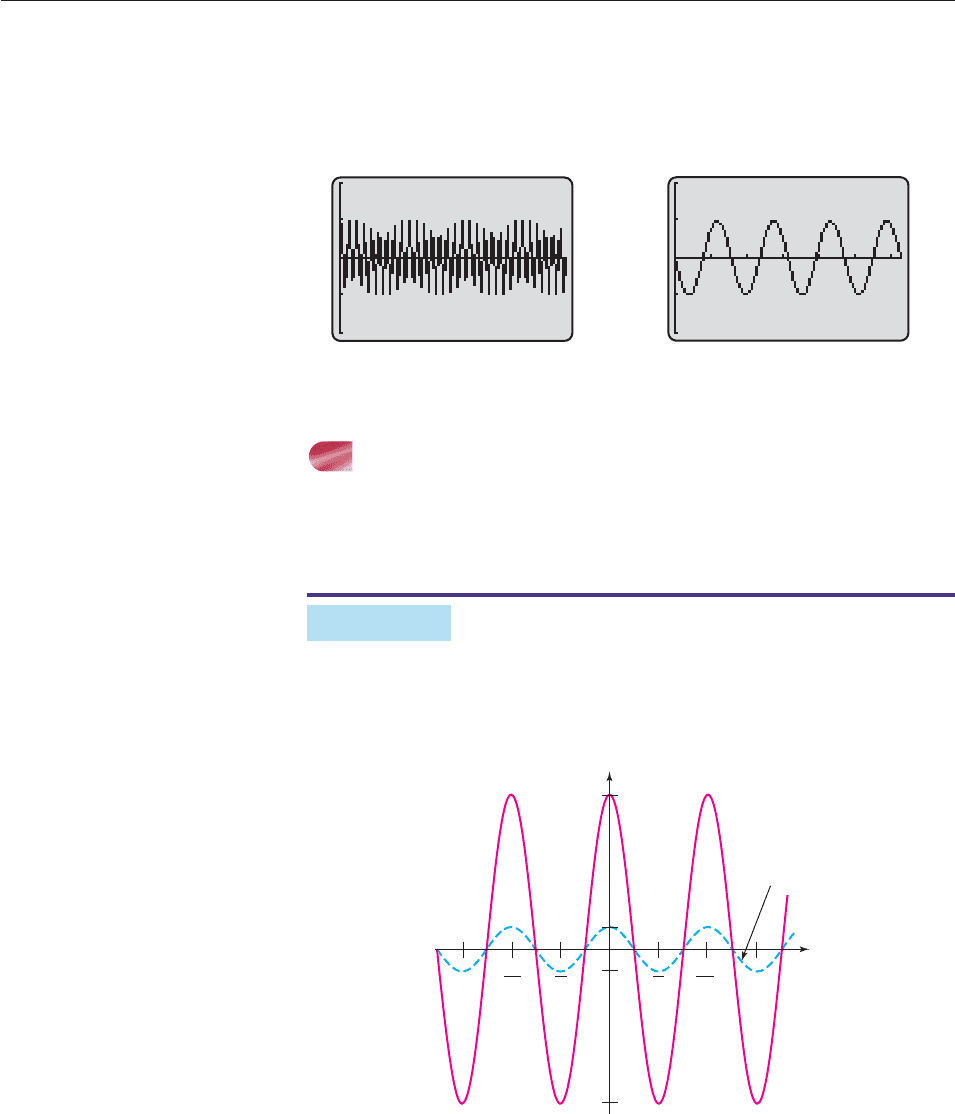
should show 500 complete waves between 0 and 2p. Depending on the model,
however, your calculator will produce either garbage (Figure 6–59) or a graph
with far fewer than 500 waves (Figure 6–60). For the reason why, see Exercises
59 and 60. ■
SECTION 6.5 Periodic Graphs and Simple Harmonic Motion 479
−2
2
02π
−2
2
02π
Figure 6–59
Figure 6–60
AMPLITUDE
As we saw in Section 3.4, multiplying the rule of a function by a positive constant
has the effect of stretching its graph away from or shrinking it toward the hori-
zontal axis.
EXAMPLE 4
The function g(t) 7 cos 3t is just the function k(t) cos 3t multiplied by 7. Con-
sequently, the graph of g is just the graph of k (which was obtained in Example 1)
stretched away from the horizontal axis by a factor of 7, as shown in Figure 6–61.
g(t) = 7 cos 3t
k(t) = cos 3t
−π
−−
7
−7
−1
t
y
1
π
3
π
3
2ππ
3
2π
3
Figure 6–61
Stretching the graph affects only the height of the waves, not the period of the func-
tion: Both graphs have period 2p/3, and each full wave has length 2p/3. ■
The waves of the graph of g(t) 7 cos 3t in Figure 6–61 rise 7 units above
the t-axis and drop 7 units below the axis. More generally, the waves of the graph
of f (t) A sin bt or g(t) A cos bt move a distance of A units above and below
the t-axis, and we say that these functions have amplitude A. In summary, we
have the following.
480 CHAPTER 6 Trigonometric Functions
Amplitude
and Period
If A 0 and b 0, then each of the functions
f (t) A sin bt or g(t) A cos bt
has amplitude A and period 2p/b.
EXAMPLE 5
The function f (t) 2 sin 4t has amplitude 2 2 and period 2p/4 p/2.
So the graph consists of waves of length p/2 that rise and fall between 2 and 2.
But be careful: The waves in the graph of 2 sin 4t (like the waves of sin t) begin at
height 0, rise, and then fall. But the graph of f (t) 2 sin 4t is the graph of
2 sin 4t reflected in the horizontal axis (see page 184). So its waves start at
height 0, move downward, and then rise, as shown in Figure 6–62. ■
f(t) =−2 sin 4t
−π
−
2
−2
−1
t
y
1
π
2
ππ
2
Figure 6–62
PHASE SHIFT
Next, we consider horizontal shifts. As we saw in Section 3.4, the graph of sin(t 3)
is the graph of sin t shifted 3 units to the right, and the graph of sin(t 3) is the
graph of sin t shifted 3 units to the left.
EXAMPLE 6
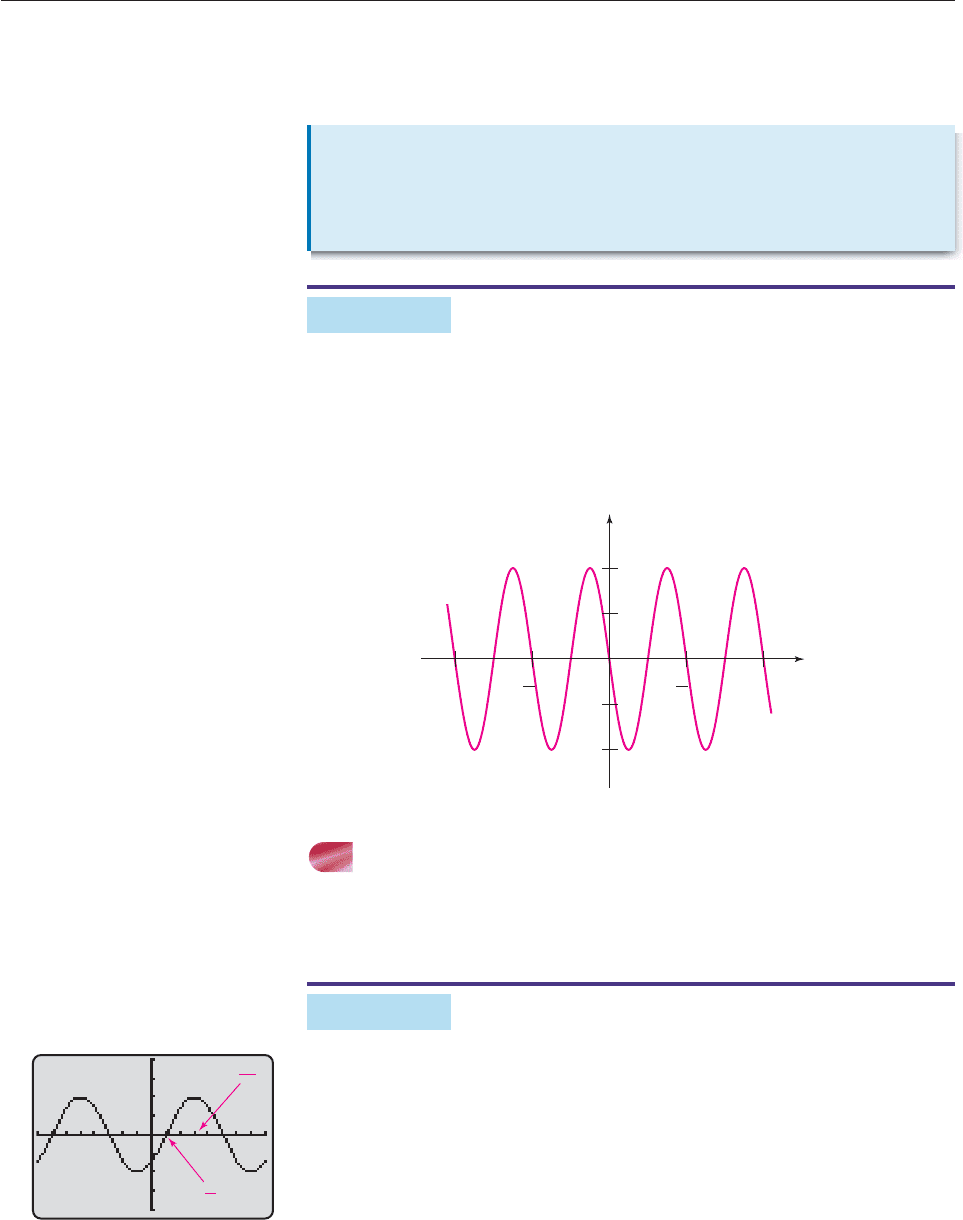
(a) Find a sine function whose graph looks like Figure 6–63.
(b) Find a cosine function whose graph looks like Figure 6–63.
SOLUTION
(a) Since each wave has height 2, Figure 6–63 looks like the graph of 2 sin t
shifted p/4 units to the right (so that a sine wave starts at t p/4). Since the
graph of 2 sin(t p/4) is the graph of 2 sin t shifted p/4 units to the right
(see page 181), we conclude that Figure 6–63 closely resembles the graph of
f (t) 2 sin(t p/4).
−4
−2π 2π
4
3π
4
π
4
2
−2
Figure 6–63

(b) Figure 6–63 also looks like the graph of 2 cos t shifted 3p/4 units to the right
(so that a cosine wave starts at t 3p/4). Hence, Figure 6–63 could also be
the graph of g(t) 2 cos(t 3p/4). ■
EXAMPLE 7
(a) Find the amplitude and the period of
f (t) 3 sin(2t 5).
(b) Do the same for the function f (t) A sin (bt c), where A, b, c are constants.
SOLUTION The analysis of f (t) 3 sin(2t 5) is in the left-hand column
below, and the analysis of the general case f (t) A sin(bt c) is in the right-hand
column. Observe that exactly the same procedure is used in both cases: Just
change 3 to A, 2 to b, and 5 to c.
SECTION 6.5 Periodic Graphs and Simple Harmonic Motion 481
(a) Rewrite the rule of f (t) 3 sin(2t 5) as (b) Rewrite the rule of f (t) A sin(bt c) as
f (t) 3 sin(2t 5) 3 sin
2
t
5
2
. f (t) A sin(bt c) A sin
b
t
b
c
.
Thus, the rule of f can be obtained from the rule Thus, the rule of f can be obtained from the rule
of the function k(t) 3 sin 2t by replacing t with of the function k(t) A sin bt by replacing t with
t
5
2
. Therefore, the graph of f is just the graph t
b
c
. Therefore, the graph of f is just the graph
of k shifted horizontally 5/2 units to the left, as of k shifted horizontally by c/b units.
shown in Figure 6–64.
Hence, f (t) 3 sin(2t 5) has the same ampli- Hence, f (t) A sin(bt c) has the same ampli-
tude as k(t) 3 sin 2t, namely, 3, and the same tude as k(t) A sin bt, namely, A, and the same
period, namely, 2p/2 p. period, namely, 2p/b.
On the graph of k(t) 3 sin 2t, a wave begins On the graph of k(t) A sin bt, a wave begins
when t 0. On the graph of when t 0. On the graph of
f (t) 3 sin 2
t
5
2
, f (t) A sin b
t
b
c
,
the shifted wave begins when t 5/2 0, that the shifted wave begins when t c/b 0, that is,
is, when t 5/2. when t c/b. ■
f(t) = 3 sin(2t + 5)
π
3
−3
−
−π
t
y
k(t) = 3 sin 2t
π
3
−3
−π
t
y
5
2
Figure 6–64

We say that the function f (t) A sin(bt c) has phase shift c/b. A similar
analysis applies to the function g(t) cos(bt c) and leads to this conclusion.
482 CHAPTER 6 Trigonometric Functions
Amplitude, Period,
and Phase Shift
If A 0 and b 0, then each of the functions
f (t) A sin(bt c) and g(t) A cos(bt c)
has
amplitude A, period 2p/b, phase shift c/b.
A wave of the graph begins at t c/b.
EXAMPLE 8
Describe the graph of g(t) 2 cos(3t 4).
SOLUTION The rule of g can be rewritten as
g(t) 2 cos(3t (4)).
This is the case described in the preceding box with A 2, b 3, and c 4.
Therefore, the function g has
amplitude A 2 2, period
2
b
p
2
3
p
,
phase shift
b
c
3
4
4
3
.
Hence, the graph of g consists of waves of length of 2p/3 that run vertically
between 2 and 2. A wave begins at t 4/3.
Verify the accuracy of this analysis by graphing y 2 cos(3t 4) in the viewing
window with 2p t 2p and 3 y 3.
GRAPHING EXPLORATION
Many other types of trigonometric graphs, including those consisting of
waves of varying height and length, are considered in Special Topics 6.5.A.
APPLICATIONS
The sine and cosine functions, or variations of them, can be used to describe many
different phenomena.
EXAMPLE 9
A typical person’s blood pressure can be modeled by the function
f (t) 22 cos(2.5pt) 95,
where t is time (in seconds) and f (t) is in millimeters of mercury. The highest pres-
sure (systolic) occurs when the heart beats, and the lowest pressure (diastolic)
■
occurs when the heart is at rest between beats. The blood pressure is the ratio
systolic/diastolic.
(a) Graph the blood pressure function over a period of two seconds and deter-
mine the person’s blood pressure.
(b) Find the person’s pulse rate (number of heartbeats per minute).
SOLUTION
(a) The graph of f is shown in Figure 6–65. The systolic pressure occurs at
each local maximum of the graph and the diastolic pressure at each local
minimum. Their heights can be determined by using our knowledge of
periodic functions. The graph of f is the graph of 22 cos(2.5pt) shifted
upward by 95 units (as explained in Section 3.4). Since the amplitude of
22 cos(2.5pt) is 22, its graph rises 22 units above and falls 22 units
below the x-axis. When this graph is shifted 95 units upward, it rises and
falls 22 units above and below the horizontal line y 95 (see Figure
6–66), that is
from a high of 95 22 117 to a low of 95 22 73.
In other words, the systolic pressure is 117 and the diastolic pressure is 73. So the
person’s blood pressure is 117/73.
SECTION 6.5 Periodic Graphs and Simple Harmonic Motion 483
150
0
0
95
2
Figure 6–66
Use a maximum/minimum finder to confirm that the local maxima of the graph in
Figure 6–65 occur when y 117 and the local minima when y 73.
GRAPHING EXPLORATION
(b) The time between heartbeats is the horizontal distance between peaks of the
graph, that is, the period of the function. The period of cos(2.5pt) is
2
b
p
2
2
.5
p
p
.8 second.
Since one minute is 60 seconds, the number of beats per minute (pulse rate) is
6
.8
0
75. ■
EXAMPLE 10
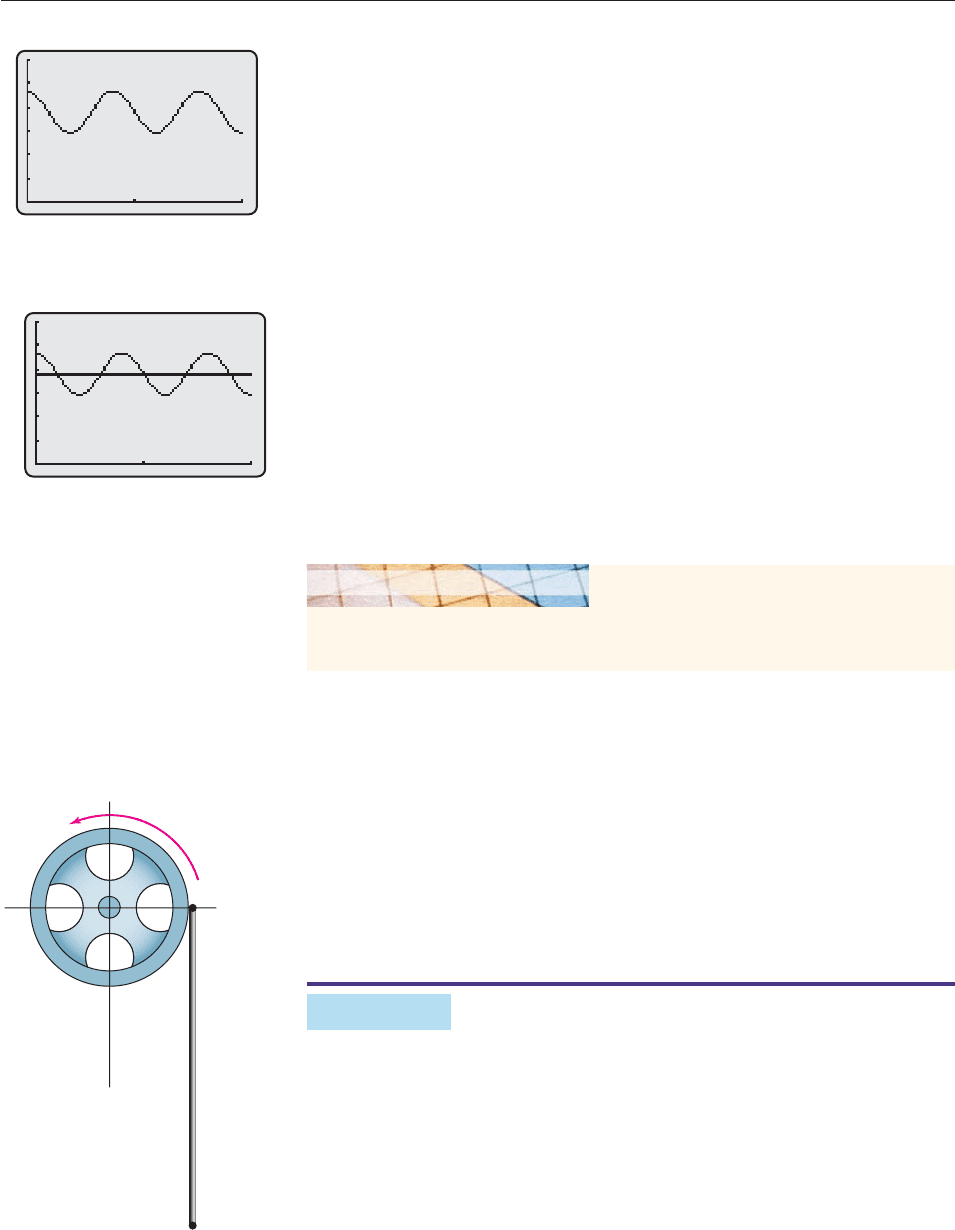
A wheel of radius 2 centimeters is rotating counterclockwise at 3 radians per
second. A free-hanging rod 10 centimeters long is connected to the edge of the
wheel at point P and remains vertical as the wheel rotates (Figure 6–67).
Assuming that the center of the wheel is at the origin and that P is at (2, 0) at
time t 0, find a function that describes the y-coordinate of the tip E of the rod
at time t.
SOLUTION The wheel is rotating at 3 radians per second, so after t seconds,
the point P has moved through an angle of 3t radians and is 2 units from the
P
E
Figure 6–67
150
0
02
Figure 6–65
origin, as shown in Figure 6–68. By the point-in-the-plane description, the coor-
dinates (x, y) of P satisfy
2
x
cos 3t
2
y
sin 3t
x 2 cos 3ty 2 sin 3t.
Since E lies 10 centimeters directly below P, its y-coordinate is 10 less than the
y-coordinate of P. Hence, the function giving the y-coordinate of E at time t is
f (t) y 10 2 sin 3t 10. ■
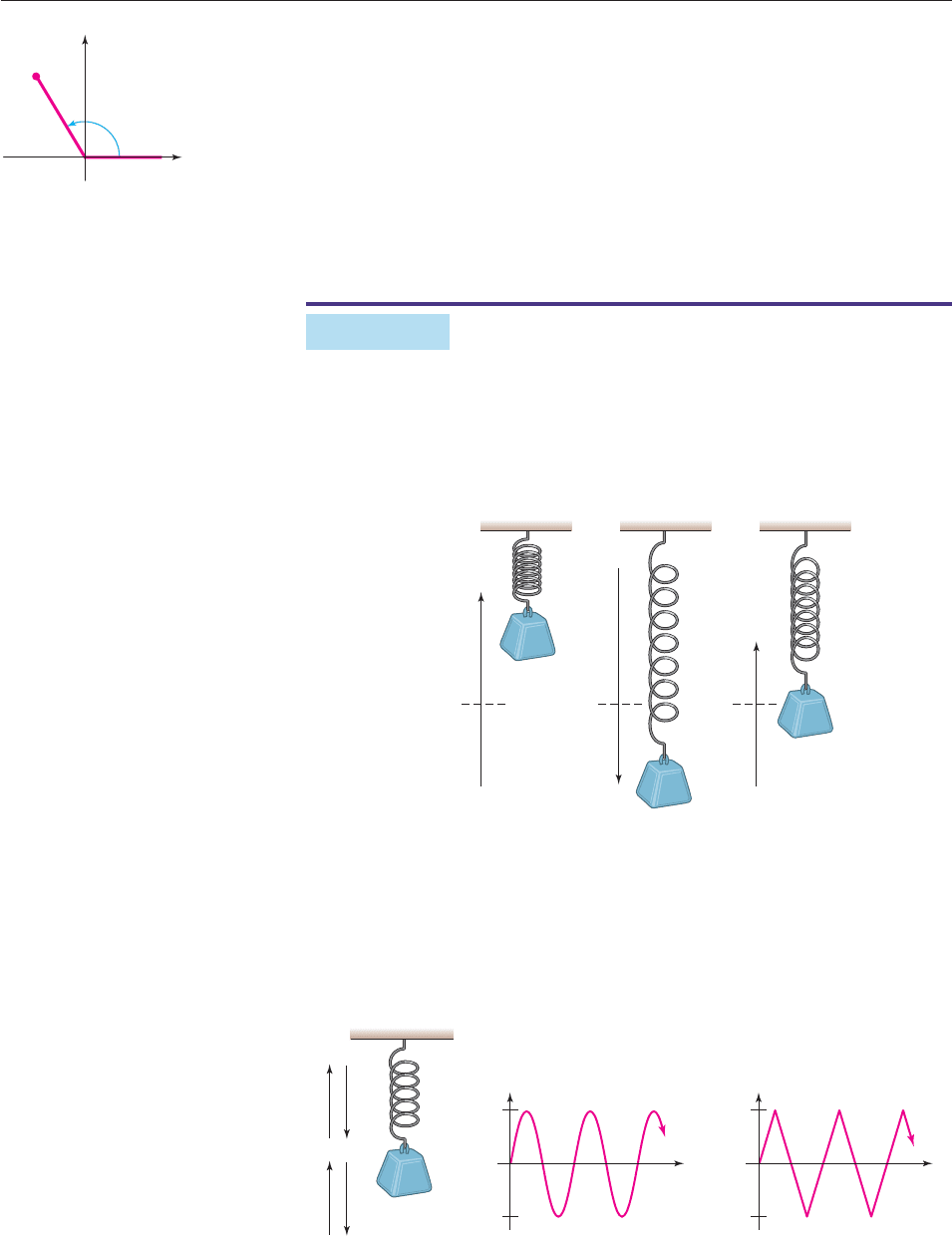
EXAMPLE 11
Suppose that a weight hanging from a spring is set in motion by an upward push
(Figure 6–69) and that it takes 5 seconds for it to move from its equilibrium posi-
tion to 8 centimeters above, then drop to 8 centimeters below, and finally return to
its equilibrium position. [We consider an idealized situation in which the spring
has perfect elasticity and friction, air resistance, etc., are negligible.]
484 CHAPTER 6 Trigonometric Functions
(x, y)
2
3t
x
y
P
Figure 6–68
Equilibrium
position
Figure 6–69
Let h(t) denote the distance of the weight above () or below () its equilibrium
position at time t. Then h(t) is 0 when t 0. As t runs from 0 to 5, h(t) increases
from 0 to 8, decreases to 8, and increases again to 0. In the next 5 seconds, it
repeats the same pattern, and so on. Thus, the graph of h has some kind of wave
shape. Two possibilities are shown in Figure 6–70.
8
or
−8
h(t)
t
8
−8
h(t)
t
Figure 6–70
Careful physical experimentation suggests that the left-hand curve in Fig-
ure 6–70, which resembles the sine graphs studied earlier, is a reasonably accurate
model of this process. Facts from physics, calculus, and differential equations
show that the rule of the function h is the form h(t) A sin(bt c) for some con-
stants A, b, c. Since the amplitude of h is 8, its period is 5, and its phase shift is 0,
the constants A, b, and c must satisfy
A 8,
2
b
p
5,
b
c
0
or, equivalently,
A 8 b
2
5
p
, c 0.
Therefore, the motion of the moving spring can be described by the function
h(t) A sin(bt c) 8 sin
2
5
p
t 0
8 sin
2
5
pt
. ■
Motion that can be described by a function of the form f (t) A sin(bt c)
or f (t) A cos(bt c) is called simple harmonic motion. Many kinds of physi-
cal motion are simple harmonic motions. Other periodic phenomena, such as
sound waves, are more complicated to describe. Their graphs consist of waves of
varying amplitude. Such graphs are discussed in Special Topics 6.5.A.
EXAMPLE 12*
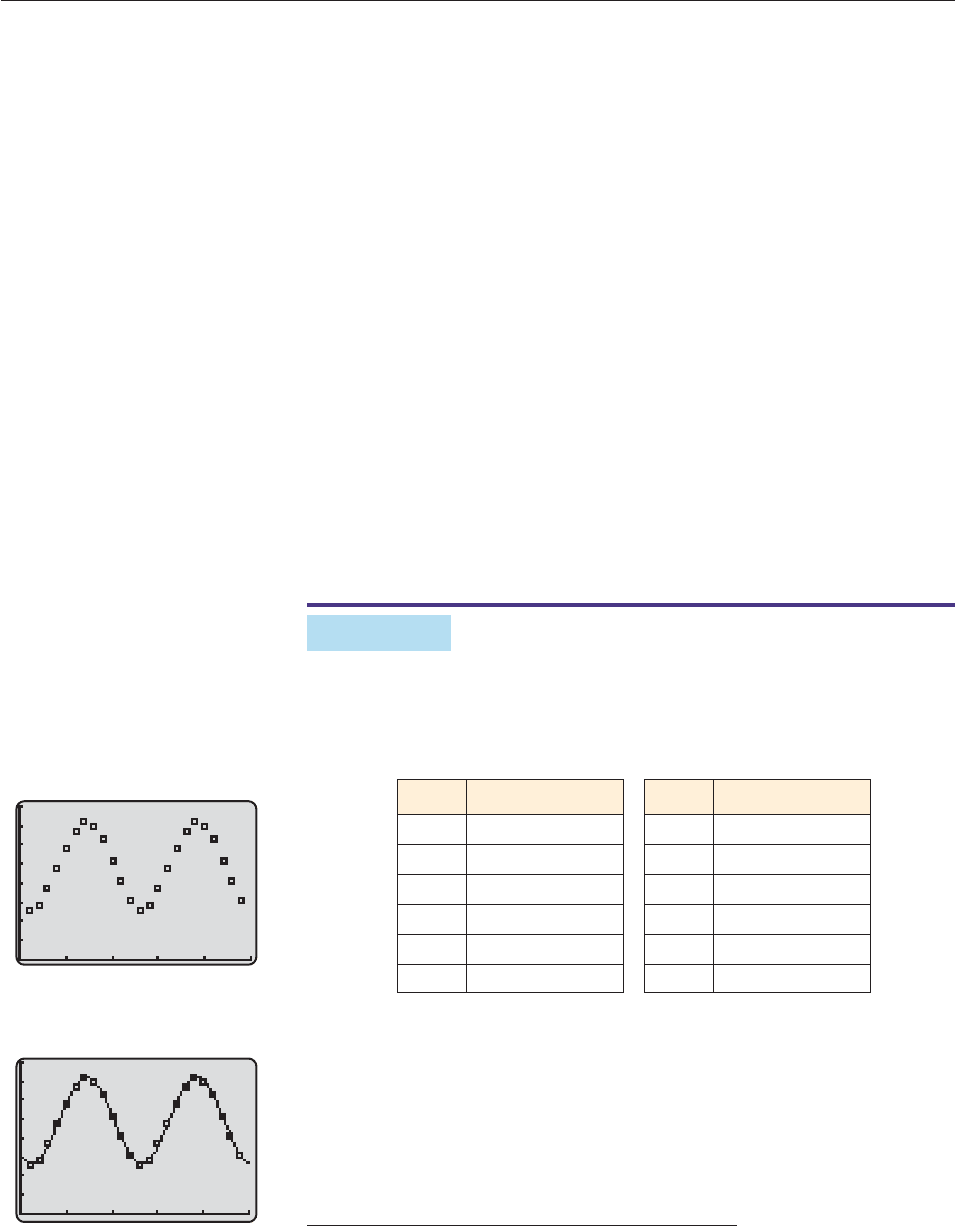
The table shows the average monthly temperature in Cleveland, OH, based on 30
years of data from the National Climatic Data Center. Since average temperatures
are not likely to vary much from year to year, the data essentially repeats the same
pattern in subsequent years. So a periodic model is appropriate.
SECTION 6.5 Periodic Graphs and Simple Harmonic Motion 485
Month Temperature (°F)
Jan 25.7
Feb 28.4
Mar 37.5
Apr 47.6
May 58.5
Jun 67.5
Month Temperature (°F)
Jul 71.9
Aug 70.2
Sep 63.3
Oct 52.2
Nov 41.8
Dec 31.1
The data for a two-year period is plotted in Figure 6–71 (with x 1 correspon-
ding to January, x 2 to February, and so on).
†
The sine regression feature on a
calculator produces this model from the 24 data points:
y 22.7 sin(.5219x 2.1842) 49.5731.
The period of this function is 2p/.5219 12.04 slightly off from the 12-month
period we would expect. However, its graph in Figure 6–72 appears to fit the data
well. ■
*Skip this example if you haven’t read Sections 2.5 and 5.5 on regression.
†
The reasons why a two-year period is used are considered in Exercises 62 and 63.
0
80
025
Figure 6–71
0
80
025
Figure 6–72
