Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


(b) An angle of p/2 radians (Figure 6–34) has its terminal side on the positive
y-axis and intersects the unit circle at P (0, 1).
cos
p
2
x-coordinate of P 0
sin
p
2
y-coordinate of P 1
tan
p
2
c
s
o
in
s
(
(
p
p
/
/
2
2
)
)
1
0
undefined. ■
The definitions of sine and cosine show that sin t and cos t are defined for
every real number t. Example 5(b), however, shows that tan t is not defined when
the x-coordinate of the point P is 0. This occurs when P has coordinates (0, 1) or
(0, 1), that is, when t p/2, 3p/2, 5p/2, etc. Consequently, the domain
(set of inputs) of each trigonometric function is as follows.
456 CHAPTER 6 Trigonometric Functions
π
1
2
−1
x
P
y
Figure 6–34
Function Domain
f(t) sin t All real numbers
g(t) cos t All real numbers
h(t) tan t All real numbers except
p/2, 3p/2, 5p/2, . . .
SPECIAL VALUES
The trigonometric functions can be evaluated exactly at t p/3, t p/4,
t p/6, and any integer multiples of these numbers by using the following facts
(which are explained in Examples 2–4 of the Geometry Review Appendix).*
A right triangle with hypotenuse A right triangle with hypotenuse
1 and angles of p/6 and p/3 1 and two angles of p/4 radians
radians has sides of lengths 1/2 has two sides of length 2
/2.
(opposite the angle of p/6) and
3
/2 (opposite the angle of p/3).
1
2
3
1
2
π
2
π
3
π
6
2
1
2
π
2
π
4
π
4
2
2
Figure 6–35
EXAMPLE 6
Evaluate the trigonometric functions at 5p/4.
SOLUTION Construct an angle of 5p/4 radians in standard position and let
P be the point where the terminal side intersects the unit circle. Draw a vertical
*Angles in the Geometry Review are given in degree measure: 60°, 45°, 30° instead of radian measure
p/3, p/4, p/6, as is done here.
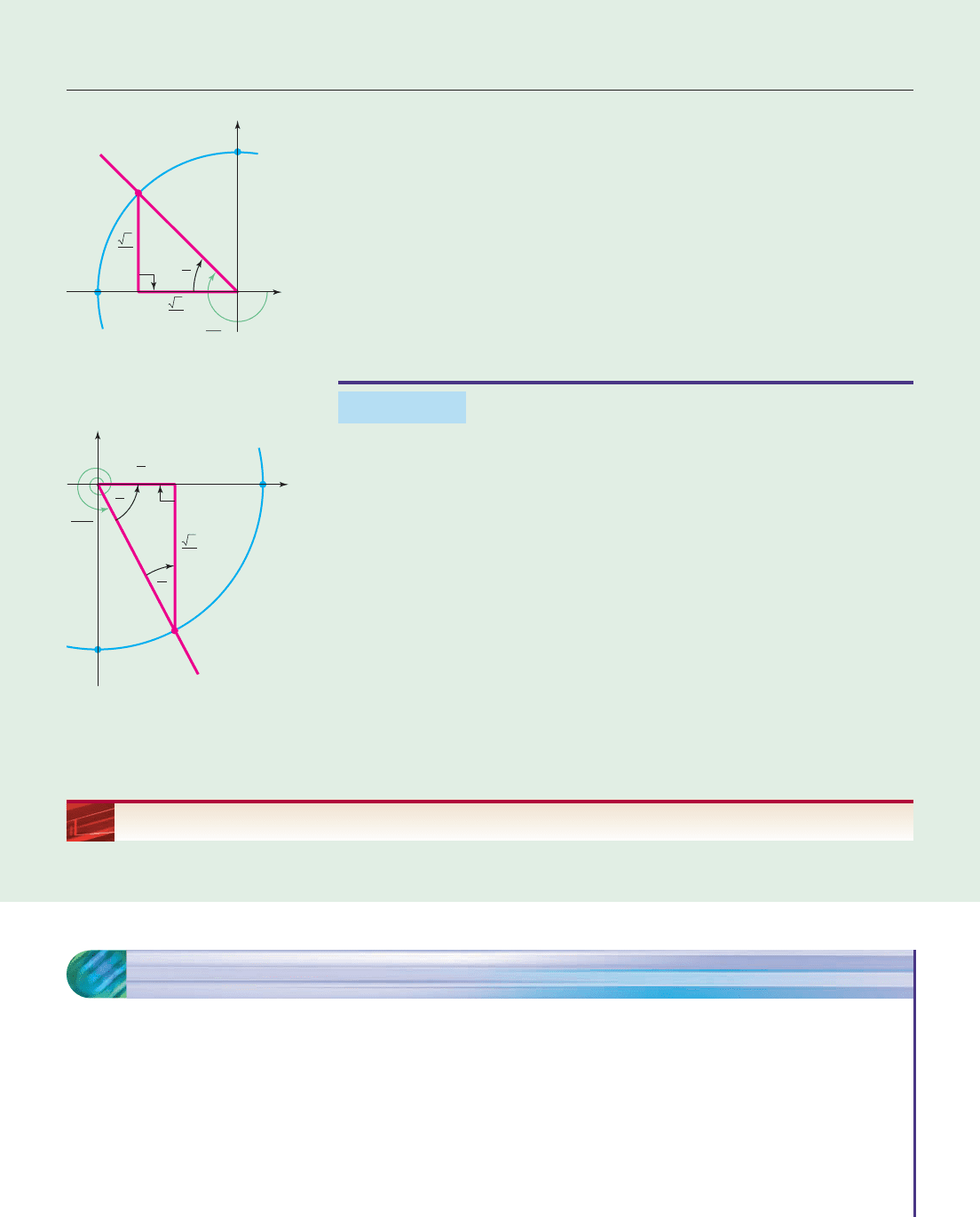
line from P to the x-axis, as shown in Figure 6–36, forming a right triangle that
matches the second triangle in Figure 6–35. The sides of the triangle in Figure
6–35 show that P has coordinates (2
/2, 2
/2). Hence,
sin
4
5p
y-coordinate of P
2
2
cos
4
5p
x-coordinate of P
2
2
tan
4
5p
c
s
o
in
s
t
t
2
2
/
/
2
2
1. ■
EXAMPLE 7
Evaluate the trigonometric functions at 11p/3.
SOLUTION Construct an angle of 11p/3 radians in standard position and
draw a vertical line from the x-axis to the point P where the terminal side of the
angle meets the unit circle, as shown in Figure 6–37. The right triangle formed in
this way matches the first triangle in Figure 6–35. The sides of the triangle in
Figure 6–36, show that the coordinates of P are (1/2, 3
/2). Therefore,
sin
11
3
p
y-coordinate of P
2
3
cos
11
3
p
x-coordinate of P
1
2
tan
11
3
p
(
(
c
s
o
in
s
1
1
1
1
p
p
/
/
3
3
)
)
1/
3
2
/2
3
. ■
SECTION 6.3 Algebra and Identities 457
2
1
⫺1
2
π
4
2
2
5π
4
1
x
P
y
⫺
Figure 6–36
3
1
2
π
6
π
3
1
2
11π
3
1
−1
x
P
y
Figure 6–37
EXERCISES ALTERNATE 6.2
Use the exercises for Section 6.2 on page 449.
6.3 Algebra and Identities
■ Learn how functional notation is used with trigonometric
functions.
■ Apply the rules of algebra to trigonometric functions.
■ Use the Pythagorean identity to evaluate and simplify
trigonometric expressions.
■ Use the periodic identities to evaluate trigonometric expressions.
■ Use the negative angle identities to evaluate and simplify
trigonometric expressions.
Section Objectives

In the previous section, we concentrated on evaluating the trigonometric func-
tions. In this section, the emphasis is on the algebra of such functions. When deal-
ing with trigonometric functions, two conventions are normally observed:
1. Parentheses are omitted whenever no confusion can result.
For example,
sin(t) is written sin t
(cos(5t)) is written cos 5t
4(tan t) is written 4 tan t.
On the other hand, parentheses are needed to distinguish
cos(t 3) from cos t 3,
because the first one says, “Add 3 to t and take the cosine of the result,”
but the second one says, “Take the cosine of t and add 3 to the result.” When
t 5, for example, these are different numbers, as shown in Figure 6–38.*
Figure 6–38
2. When dealing with powers of trigonometric functions, positive expo-
nents are written between the function symbol and the variable.
For example,
(cos t)
3
is written cos
3
t
(sin t)
4
(tan 7t)
2
is written sin
4
t tan
2
7t.
Furthermore,
sin t
3
means sin(t
3
)[not (sin t)
3
or sin
3
t]
For instance, when t 4, we have Figure 6–39.
Figure 6–39
Except for these two conventions and the Caution in the margin, the algebra
of trigonometric functions is just like the algebra of other functions. They may be
added, subtracted, multiplied, composed, etc.
458 CHAPTER 6 Trigonometric Functions
*Figures 6–38 and 6–39 show a TI-86 screen.
TECHNOLOGY TIP
TI-84 and HP-39gs automatically
insert an opening parenthesis when
the COS key is pushed. The display
COS(5 3 is interpreted as
COS(5 3). If you want cos 5 3,
you must insert a parenthesis after the
5: COS(5) 3.
TECHNOLOGY TIP
Calculators do not use convention 2. To
obtain sin
3
4, you must enter (sin 4)
3
.
CAUTION
Convention 2 is not used when the
exponent is 1. For example, sin
1
t
does not mean (sin t )
1
or 1/(sin t );
it has an entirely different meaning
that will be discussed in Section 7.4.
Similar remarks apply to cos
1
t and
tan
1
t.
Section 8.1 may be covered at
this point by instructors who
prefer to introduce right triangle
trigonometry early.
Roadmap
EXAMPLE 1
If f (t) sin
2
t tan t and g(t) tan
3
t 5, then the product function fg is given
by the rule
( fg)(t) f (t)g(t) (sin
2
t tan t)(tan
3
t 5)
sin
2
t tan
3
t 5 sin
2
t tan
4
t 5 tan t. ■
EXAMPLE 2
Factor 2 cos
2
t 5 cos t 3.
SOLUTION You can do this directly, but it may be easier to understand if you
make a substitution. Let u cos t, then
2 cos
2
t 5 cos t 3 2(cos t)
2
5 cos t 3
2u
2
5u 3
(2u 1)(u 3)
(2 cos t 1)(cos t 3). ■
EXAMPLE 3
If f (t) cos
2
t 9 and g(t) cos t 3, then the quotient function f/g is given by
the rule
g
f
(t)
g
f (
(
t
t
)
)
c
c
o
o
s
s
2
t
t
3
9
cos t 3. ■
EXAMPLE 4
If f (t) sin t and g(t) t
2
3, then the composite function g f is given by the rule
(g f )(t) g( f (t)) g(sin t) sin
2
t 3.
The composite function f g is given by the rule
( f g)(t) f (g(t)) f (t
2
3) sin(t
2
3).
The parentheses are crucial here because sin(t
2
3) is not the same function as
sin t
2
3. For instance, a calculator in radian mode shows that for t 5,
sin(5
2
3) sin(25 3) sin 28 .2709,
(cos t 3)(cos t 3)
cos t 3
SECTION 6.3 Algebra and Identities 459
CAUTION
You are dealing with functional notation here, so the symbol sin t is a single entity, as are cos t
and tan t. Don’t try some nonsensical “canceling” operation, such as
c
s
o
in
s
t
t
c
s
o
in
s
or
c
c
o
o
s
s
t
t
2
c
c
o
o
s
s
t
t.
whereas
sin 5
2
3 sin 25 3 (.1324) 3 2.8676. ■
THE PYTHAGOREAN IDENTITY
Trigonometric functions have numerous interrelationships that are usually
expressed as identities. An identity is an equation with this property: For every
value of the variable for which both sides of the equation are defined, the equation
is true. Here is one of the most important trigonometric identities.
Proof For each real number t, the point P, where the terminal side of an angle
of t radians intersects the unit circle, has coordinates (cos t, sin t), as in Fig-
ure 6–40. Since P lies on the unit circle, its coordinates must satisfy the equation
of the unit circle: x
2
y
2
1, that is, cos
2
t sin
2
t 1. ■
EXAMPLE 5
If p/2 t p and sin t 2/3, find cos t and tan t.
SOLUTION By the Pythagorean identity,
cos
2
t 1 sin
2
t 1
2
3
2
1
4
9
5
9
.
So there are two possibilities:
cos t 5/9
5
/3orcost 5/9
5
/3.
Since p/2 t p, cos t is negative (see Exercise 63 on page 451). Therefore,
cos t 5
/3, and
tan t
c
s
o
in
s
t
t
2/
5
3
/3
2
5
2
5
5
. ■
EXAMPLE 6
The Pythagorean identity is valid for any number t. For instance, if t 3k 7,
then sin
2
(3k 7) cos
2
(3k 7) 1. ■
460 CHAPTER 6 Trigonometric Functions
Pythagorean
Identity
For every real number t,
sin
2
t cos
2
t 1.
Recall that the graph of y 1 is a horizontal line through (0, 1). Verify the
Pythagorean identity by graphing the equation
y (sin x)
2
(cos x)
2
in the window with 10 x 10 and 3 y 3 and using the trace feature.
GRAPHING EXPLORATION
1
−1
−1
1
(cos t, sin t)
x
P
t
y
Figure 6–40

EXAMPLE 7
To simplify the expression tan
2
t cos
2
t cos
2
t, we use the definition of tangent and
the Pythagorean identity:
tan
2
t cos
2
t cos
2
t
c
s
o
in
s
2
2
t
t
cos
2
t cos
2
t
sin
2
t cos
2
t 1. ■
For every real number t, the point (cos t, sin t) is on the unit circle, as illus-
trated in Figure 6–40. Since the coordinates of any point on the unit circle are
between 1 and 1, we have this useful fact:
As we shall see in Section 6.4,
The range of the tangent function consists of all real numbers.
You can confirm this fact by doing the following Exploration.
SECTION 6.3 Algebra and Identities 461
Range of Sine
and Cosine
For every real number t
1 sin t 1
and
1 cos t 1.
Use the table feature to evaluate tan
p
2
x
when x .01, .001, .0001, and so on.
What does this suggest about the outputs of the tangent function? Now evaluate
when x .01, .001, .0001, and so on, and answer the same question.
CALCULATOR EXPLORATION
PERIODICITY IDENTITIES
Let t be any real number and construct two angles in standard position of measure
t and t 2p radians, respectively, as shown in Figure 6–41. As we saw in Section
6.1, both of these angles have the same terminal side. Therefore, the point P where
the terminal side meets the unit circle is the same in both cases.
Figure 6–41
(cos t, sin t)
x
P
t
y
(cos (t + 2π), sin (t + 2π))
t + 2π
x
P
y

Therefore, the coordinates of P are the same, that is,
sin t sin(t 2p) and cos t cos(t 2p).
Furthermore, since an angle of t radians has the same terminal side as angles of
radian measure t 2p, t 4p, t 6p, and so forth, the same argument shows that
sin t sin(t 2p) sin(t 4p) sin(t 6p)
. . .
cos t cos(t 2p) cos(t 4p) cos(t 6p)
. . .
as illustrated (for t 5) in Figure 6–42.
There is a special name for functions that repeat their values at regular inter-
vals. A function f is said to be periodic if there is a positive constant k such that
f (t) f (t k) for every number t in the domain of f. There will be more than one
constant k with this property; the smallest one is called the period of the function f.
We have just seen that sine and cosine are periodic with k 2p. Exercises 69 and
70 show that 2p is the smallest such positive constant k. Therefore, we have the
following.
462 CHAPTER 6 Trigonometric Functions
Figure 6–42
Period of Sine
and Cosine
The sine and cosine functions are periodic with period 2p: For every real
number t,
sin t sin(t 2p) sin(t 4p) sin(t 6p)
. . .
and
cos t cos(t 2p) cos(t 4p) cos(t 6p)
. . .
EXAMPLE 8
As we saw in Examples 3 and 5 of Section 6.2, sin
p
6
1
2
and cos
5
4
p
2
2
. Use these facts to find
(a) sin
13
6
p
(b) cos
29
4
p
.
SOLUTION The key is to write the given number as a sum in which one sum-
mand is an even multiple of p, and then apply a periodicity identity.
(a) sin
13
6
p
sin
p
6
12
6
p
sin
p
6
2p
sin
p
6
1
2
[Periodicity Identity]
(b) cos
29
4
p
cos
5
4
p
24
4
p
cos
5
4
p
6p
cos
5
4
p
2
2
[Periodicity Identity] ■
The tangent function is also periodic (see Exercise 36), but its period is p
rather than 2p, that is,
tan(t p) tan t for every real number t,
as we shall see in Section 6.4.
NEGATIVE ANGLE IDENTITIES
The preceding Graphing Exploration suggests the truth of the following
statement.
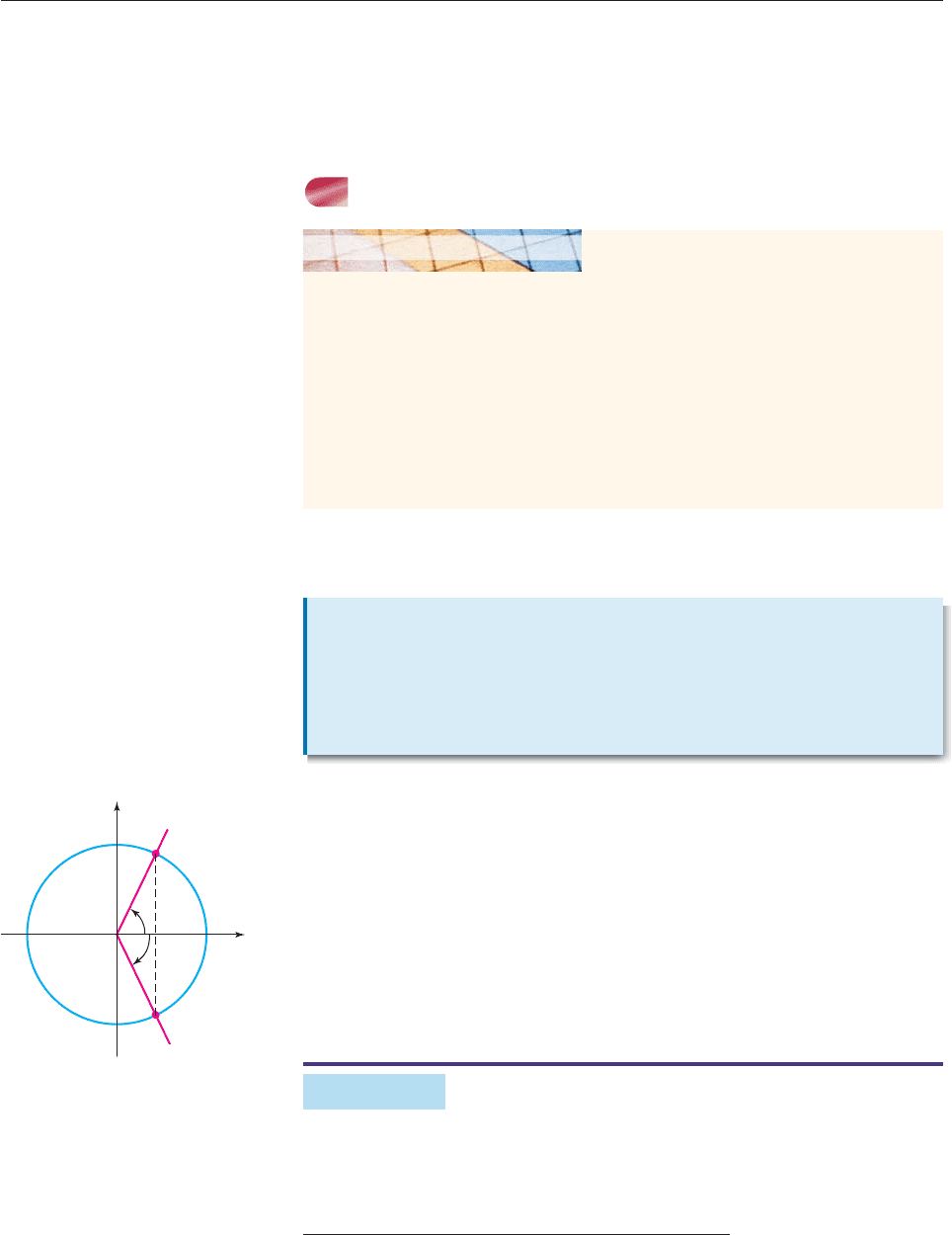
Proof Consider angles of t radians and t radians in standard position, as in
Figure 6–43. By the definition of sine and cosine, P has coordinates (cos t, sin t),
and Q has coordinates (cos(t), sin(t)). As Figure 6–43 suggests, P and Q lie on
the same vertical line. Therefore, they have the same first coordinate, that is,
cos(t) cos t. As the figure also suggests, P and Q lie at equal distances from
the x-axis.* So the y-coordinate of Q must be the negative of the y-coordinate of
P, that is, sin(t) sin t. Finally, by the definition of the tangent function and
the two identities just proved, we have
tan(t)
c
s
o
in
s
(
(
t
t
)
)
co
si
s
n
t
t
c
s
o
in
s
t
t
tan t. ■
EXAMPLE 9
In Example 3 of Section 6.2, we showed that
sin
p
6
1
2
, cos
p
6
2
3
, tan
p
6
3
3
.
SECTION 6.3 Algebra and Identities 463
(a) In a viewing window with 2p x 2p, graph y
1
sin x and y
2
sin(x)
on the same screen. Use trace to move along y
1
sin x. Stop at a point and note
its y-coordinate. Use the up or down arrow to move vertically to the graph of
y
2
sin(x). The x-coordinate remains the same, but the y-coordinate is differ-
ent. How are the two y-coordinates related? Is one the negative of the other?
Repeat the procedure for other points. Are the results the same?
(b) Now graph y
1
cos x and y
2
cos(x) on the same screen. How do the graphs
compare?
(c) Repeat part (a) for y
1
tan x and y
2
tan(x). Are the results similar to those
for sine?
GRAPHING EXPLORATION
Negative Angle
Identities
For every real number t,
sin(t) sin t
cos(t) cos t
tan(t) tan t.
(cos t, sin t)
(cos (−t), sin (−t))
t
−t
−1
−11
1
x
P
Q
y
Figure 6–43
*These facts can be proved by using congruent triangles. (See Exercise 13 in the Geometry Review
Appendix.)
Using the negative angle identities, we have
sin
p
6
sin
p
6
1
2
, cos
p
6
cos
p
6
2
3
,
tan
p
6
tan
p
6
3
3
. ■
EXAMPLE 10
To simplify (1 sin t)(1 sin(t)), we use the negative angle identity and the
Pythagorean identity.
(1 sin t)(1 sin(t)) (1 sin t)(1 sin t)
1 sin
2
t
cos
2
t. ■
464 CHAPTER 6 Trigonometric Functions
EXERCISES 6.3
In Exercises 1–4, find the rule of the product function fg.
1. f(t) 3 sin t; g(t) sin t 2 cos t
2. f(t) 5 tan t; g(t) tan
3
t 1
3. f(t) 3 sin
2
t; g(t) sin t tan t
4. f(t) sin 2t cos
4
t; g(t) cos 2t cos
2
t
In Exercises 5–14, factor the given expression.
5. cos
2
t 4 6. 25 tan
2
t
7. sin
2
t cos
2
t 8. sin
3
t sin t
9. tan
2
t 6 tan t 9 10. cos
2
t cos t 2
11. 6 sin
2
t sin t 1 12. tan t cos t cos
2
t
13. cos
4
t 4 cos
2
t 5 14. 3 tan
2
t 5 tan t 2
In Exercises 15–18, find the rules of the composite functions
f g and g f.
15. f (t) cos t; g(t) 2t 4
16. f (t) sin t 2; g(t) t
2
17. f(t) tan(t 3); g(t) t
2
1
18. f(t) cos
2
(t 2); g(t) 5t 2
In Exercises 19–24, determine if it is possible for a number t to
satisfy the given conditions. [Hint: Think Pythagorean.]
19. sin t 5/13 and cos t 12/13
20. sin t 2 and cos t 1
21. sin t 1 and cos t 1
22. sin t 1/2
and cos t 1/2
23. sin t 1 and tan t 1
24. cos t 8/17 and tan t 15/8
In Exercises 25–28, use the Pythagorean identity to find sin t.
25. cos t .5 and p t 3p/2
26. cos t 3/10 and p/2 t p
27. cos t 1/2 and 0 t p/2
28. cos t 2/5
and 3p/2 t 2p
In Exercises 29–35, assume that sin t 3/5 and
0 t p/2. Use identities in the text to find the number.
29. sin(t) 30. sin(t 10p) 31. sin(2p t)
32. cos t 33. tan t 34. cos(t)
35. tan(2p t)
36. (a) Show that tan(t 2p) tan t for every t in the domain
of tan t. [Hint: Use the definition of tangent and some
identities proved in the text.]
(b) Verify that it appears true that tan(x p) tan x for
every t in the domain by using your calculator’s table
feature to make a table of values for y
1
tan(x p)
and y
2
tan x.
In Exercises 37–42, assume that
cos t 2/5 and p t 3p/2.
Use identities to find the number.
37. sin t 38. tan t 39. cos(2p t)
40. cos(t) 41. sin(4p t) 42. tan(4p t)

SECTION 6.3 Algebra and Identities 465
In Exercises 43–46, assume that
sin(p/8)
2
2
2
and use identities to find the exact functional value.
43. cos(p/8) 44. tan(p/8)
45. sin(17p/8) 46. tan(15p/8)
In Exercises 47–58, use algebra and identities in the text to
simplify the expression. Assume all denominators are nonzero.
47. (sin t cos t)(sin t cos t)
48. (sin t cos t)
2
49. tan t cos t
50. (sin t)/(tan t) 51.
sin
3
t c
os t
cos t
52. (tan t 2)(tan t 3) (6 tan t) 2 tan t
53.
4
s
c
in
o
2
s
t
2
t
4
s
c
in
os
t
t
2
54.
5
s
c
in
o
2
s
t
t
sin
s
2
i
t
n
2
t
sin
co
t
s
c
2
o
t
s t
55.
56.
sin
2
t
s
in
2
t
s
in
1
t 1
57.
co
1
s t
sin t tan t
58.
1
1
t
t
a
a
n
n
2
2
t
t
2 sin
2
t
59. The average monthly temperature in Cleveland, Ohio is
approximated by
f(t) 22.7 sin(.52x 2.18) 49.6,
where t 1 corresponds to January, t 2 to February, and
so on.
(a) Construct a table of values (t 1, 2, . . . , 12) for the
function f(t) and another table for f(t 12.083).
(b) Based on these tables would you say that the function f
is (approximately) periodic? If so, what is the period?
Is this reasonable?
60. A typical healthy person’s blood pressure can be modeled
by the periodic function
f(t) 22 cos(2.5pt) 95,
where t is time (in seconds) and f(t) is in millimeters of mer-
cury. Which one of .5, .8, or 1 appears to be the period of
this function?
61. The percentage of the face of the moon that is illuminated
(as seen from earth) on day t of the lunar month is given by
g(t) .5
1 cos
2
2
9
p
.5
t
.
(a) What percentage of the face of the moon is illuminated
on day 0? Day 10? Day 22?
cos
2
t 4 cos t 4
cos t 2
(b) Construct appropriate tables to confirm that g is a peri-
odic function with period 29.5 days.
(c) When does a full moon occur (g(t) 1)?
In Exercises 62–67, show that the given function is periodic
with period less than 2p. [Hint: Find a positive number k with
k 2p such that f (t k) f (t) for every t in the domain of f.]
62. f(t) sin 2t
63. f (t) cos 3t
64. f(t) sin 4t
65. f(t) sin(pt)
66. f (t) cos(3pt/2)
67. f(t) tan 2t
68. Fill the blanks with “even” or “odd” so that the resulting
statement is true. Then prove the statement by using an
appropriate identity. [Hint: Special Topics 3.4.A may be
helpful.]
(a) f (t) sin t is an function.
(b) g(t) cos t is an function.
(c) h(t) tan t is an function.
(d) f (t) t sin t is an function.
(e) g(t) t tan t is an function.
69. Here is a proof that the cosine function has period 2p. We
saw in the text that cos(t 2p) cos t for every t. We must
show that there is no positive number smaller than 2p with
this property. Do this as follows:
(a) Find all numbers k such that 0 k 2p and cos k 1.
[Hint: Draw a picture and use the definition of the
cosine function.]
(b) Suppose k is a number such that cos(t k) cos t for
every number t. Show that cos k 1. [Hint: Consider
t 0.]
(c) Use parts (a) and (b) to show that there is no posi-
tive number k less than 2p with the property that
cos(t k) cos t for every number t. Therefore,
k 2p is the smallest such number, and the cosine
function has period 2p.
70. Here is proof that the sine function has period 2p. We saw
in the text that sin(t 2p) sin t for every t. We must show
that there is no positive number smaller than 2p with this
property. Do this as follows:
(a) Find a number t such that sin(t p) sin t.
(b) Find all numbers k such that 0 k 2p and sin k 0.
[Hint: Draw a picture and use the definition of the sine
function.]
(c) Suppose k is a number such that sin(t k) sin t for
every number t. Show that sin k 0. [Hint: Consider
t 0.]
(d) Use parts (a)–(c) to show that there is no positive num-
ber k less than 2p with the property that sin(t k)
sin t for every number t. Therefore, k 2p is the small-
est such number, and the sine function has period 2p.
