Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


426
5. In the logistic model, the rate at which the disease spreads tends to fall over
time. This means that the value of r you calculated in Exercise 1 is a little
low. Raise the value of r and find the new value of a as in Exercise 3.
Experiment until you find a value of r for which g(7) 193 (meaning that
the model g matches the data on day 7).
6. Using the function g from Exercise 5, repeat Exercise 4.
DISCOVERY PROJECT 5

TRIGONOMETRIC FUNCTIONS
Don’t touch that dial!
Radio stations transmit by sending out a signal in the
form of an electromagnetic wave that can be described
by a trigonometric function. The shape of this signal is
modified by the sounds being transmitted. AM radio
signals are modified by varying the “height,” or
amplitude, of the waves, whereas FM signals are
modified by varying the frequency of the waves. See
Exercise 47 on page 487.
427
Chapter
© Eduardo Garcia/Getty Images
AM signal
F
M signal

428
428
Chapter Outline
Interdependence of
Sections
6.1 Angles and Their Measurement
6.1.A Special Topics: Arc Length and Angular Speed
6.2 The Sine, Cosine, and Tangent Functions
6.2 ALTERNATE The Sine, Cosine, and Tangent Functions
6.3 Algebra and Identities
6.4 Basic Graphs
6.5 Periodic Graphs and Simple Harmonic Motion
6.5.A Special Topics: Other Trigonometric Graphs
6.6 Other Trigonometric Functions
The ancient Greeks developed trigonometry for measuring angles and
sides of triangles to solve problems in astronomy, navigation, and survey-
ing.
†
But with the invention of calculus in the seventeenth century and the
subsequent explosion of knowledge in the physical sciences, a different
viewpoint toward trigonometry arose.
Whereas the ancients dealt only with angles, the classical trigono-
metric concepts of sine and cosine are now considered as functions of
real numbers. The advantage of this switch in viewpoint is that almost any
phenomenon involving rotation or repetition can be described in terms of
trigonometric functions, including light rays, sound waves, planetary
orbits, weather, animal populations, radio transmission, guitar strings,
pendulums, and many more.
The presentation of trigonometry here reflects this modern viewpoint.
Nevertheless, angles still play an important role in defining the trigono-
metric functions, so the chapter begins with them.
6.1 Angles and Their Measurement
■ Use basic terminology to describe angles.
■ Learn radian measure for angles
■ Convert the measure of an angle from radians to degree and
vice versa.
In trigonometry an angle is formed by rotating a half-line around its endpoint (the
vertex), as shown in Figure 6–1, where the arrow indicates the direction of rota-
tion. The position of the half-line at the beginning is the initial side, and its final
position is the terminal side of the angle.
*Parts of Section 6.6 may be covered much earlier; see the Roadmap at the beginning of Section 6.2.
†
In fact, “trigonometry” means “triangle measurement.”
Section Objectives
6.5
6.1 6.2 6.3 6.4
6.6*
Instructors who want to introduce
triangle trigonometry before (or
simultaneously with) trigonometric
functions of a real variable should
consult the chart on page xiv. It
provides several ways of doing
this.
Roadmap
Figure 6–1
Figure 6–2 shows that different angles (that is, angles obtained by different
rotations) may have the same initial and terminal side.* Such angles are said to be
coterminal.
Figure 6–2
An angle in the coordinate plane is said to be in standard position if its ver-
tex is at the origin and its initial side on the positive x-axis, as in Figure 6–3. When
measuring angles in standard position, we use positive numbers for angles
obtained by counterclockwise rotation (positive angles) and negative numbers for
ones obtained by clockwise rotation (negative angles).
Figure 6–3
The classical unit for angle measurement is the degree (in symbols, °), as
explained in the Geometry Review Appendix. You should be familiar with the
positive angles in standard position shown in Figure 6–4 on the next page. Note
that a 360° angle corresponds to one full revolution and thus is coterminal with
an angle of 0°.
Positive
angle
x
y
Negative
angle
x
y
Initial
Terminal
Vertex
Initial
Terminal
Initial
Initial
Initial
Terminal
Terminal
Terminal
SECTION 6.1 Angles and Their Measurement 429
*They are not the same angle, however. For instance, both
1
2
turn and 1
1
2
turns put a circular faucet
handle in the same position, but the water flow is quite different.
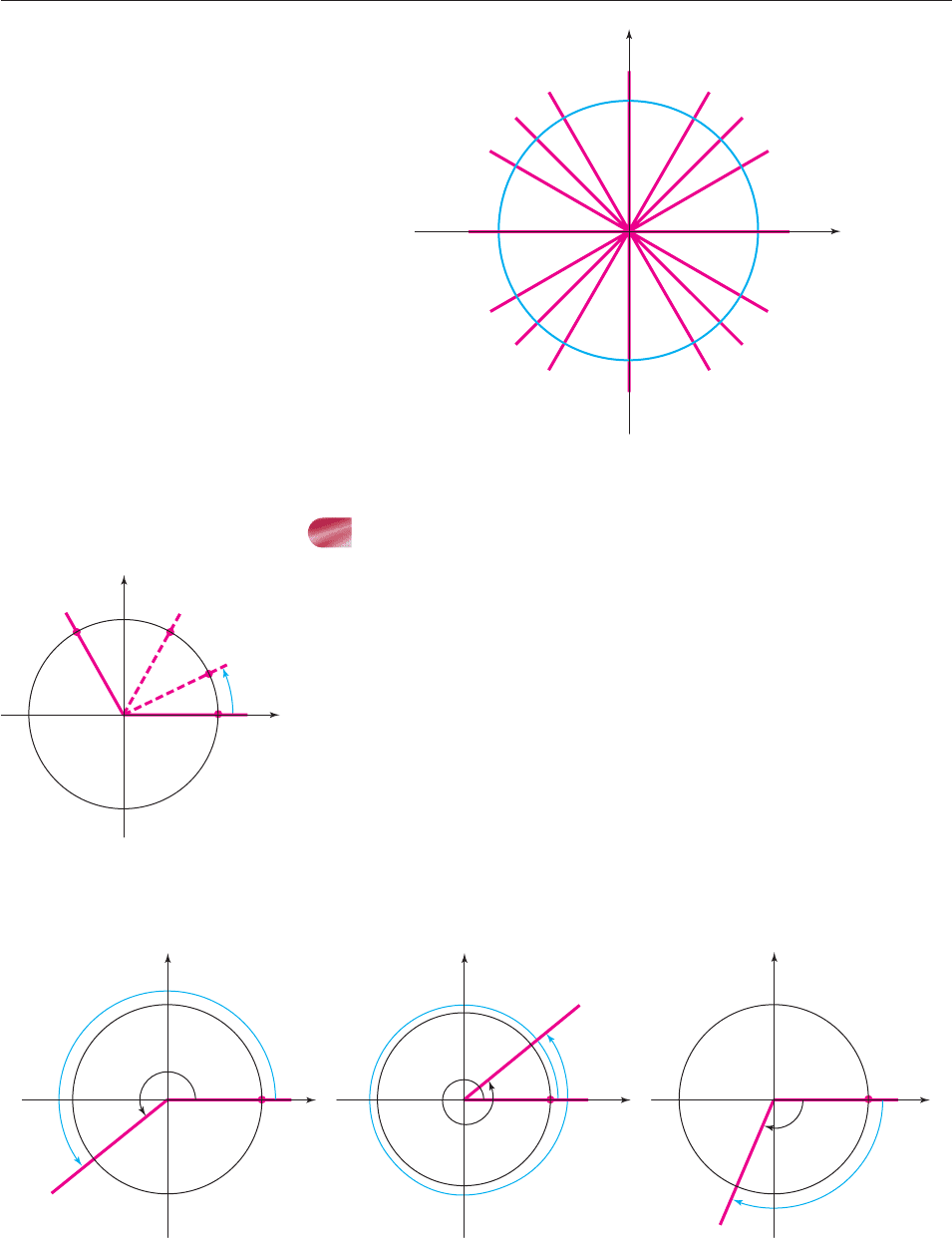
Figure 6–4
RADIAN MEASURE
Because it simplifies many formulas in calculus and physics, a different unit of
angle measurement is used in mathematical and scientific applications. Recall
that the unit circle is the circle of radius 1 with center at the origin; its equation
is x
2
y
2
1. When a positive angle in standard position is formed by rotating
the initial side (the positive x-axis) counterclockwise, then the point P (1, 0)
moves along the unit circle, as in Figure 6–5. The radian measure of the angle
is defined to be
the distance traveled along the unit circle by the point P as
it moves from its starting position on the initial side to its
final position on the terminal side of the angle.
The radian measure of a negative angle in standard position is found in the
same way, except that you move clockwise along the unit circle. Figure 6–6
shows angles of 3.75, 7, and 2 radians, respectively.
Figure 6–6
x
y
(1, 0)
Angle =
7 radians
Distance = 7
x
y
(1, 0)
Angle = −2 radians
Distance = 2
x
y
(1, 0)
Angle =
3.75 radians
Distance = 3.75
x
y
30°
45°
60°120°
135°
150°
210°
225°
240° 300°
330°
Fourth quadrantThird quadrant
First quadrantSecond quadrant
315°
270°
180°
90°
0° (360°)
430 CHAPTER 6 Trigonometric Functions
x
y
(1, 0)
P
P
P
P
Figure 6–5
To become comfortable with radian measure, think of the terminal side of
the angle revolving around the origin: When it makes one full revolution, it
produces an angle of 2p radians (because the circumference of the unit circle
is 2p). When it makes half a revolution, it forms an angle whose radian meas-
ure is 1/2of2p, that is, p radians, and so on, as illustrated in Figure 6–7 and
the table below.
1 revolution 3/4 revolution 1/2 revolution 1
1
4
revolutions
2p radians
3
4
2p
3
2
p
radians
1
2
2p p radians
5
4
2p
5
2
p
radians
Figure 6–7
Although equivalent degree measures are given in the table, you should learn
to “think in radians” as much as possible rather than mentally translating from
radians to degrees.
x
y
1
−1
−1
1
x
y
1
−1
−1
1
x
y
1
−1
−1
1
x
y
1
−1
−1
1
SECTION 6.1 Angles and Their Measurement 431
Radian Measure Equivalent Degree
Terminal Side of Angle Measure
1 revolution 2p 360°
7
8
revolution
7
8
2p
7
4
p
7
8
360 315°
3
4
revolution
3
4
2p
3
2
p
3
4
360 270°
2
3
revolution
2
3
2p
4
3
p
2
3
360 240°
1
2
revolution
1
2
2p p
1
2
360 180°
1
3
revolution
1
3
2p
2
3
p
1
3
360 120°
1
4
revolution
1
4
2p
p
2
1
4
360 90°
1
6
revolution
1
6
2p
p
3
1
6
360 60°
1
8
revolution
1
8
2p
p
4
1
8
360 45°
1
1
2
revolution
1
1
2
2p
p
6
1
1
2
360 30°

EXAMPLE 1
To construct an angle of 16p/3 radians in standard position, note that
16
3
p
6
3
p
6
3
p
4
3
p
2p 2p
4
3
p
.
So the terminal side must be rotated counterclockwise through two complete rev-
olutions (each full-circle revolution is 2p radians) and then rotated an additional
2/3 of a revolution (since 4p/3 is 2/3 of a complete revolution of 2p radians),
as shown in Figure 6–8. ■
EXAMPLE 2
Since 5p/4 p p/4, an angle of 5p/4 radians in standard position is
obtained by rotating the terminal side clockwise for half a revolution (p radians)
plus an additional 1/8 of a revolution (since p/4 is 1/8 of a full-circle revolution
of 2p radians), as shown in Figure 6–9. ■
Consider an angle of t radians in standard position (Figure 6–10). Since 2p
radians corresponds to a full revolution of the terminal side, this angle has the
same terminal side as an angle of t 2p radians or t 2p radians or t 4p
radians.
Figure 6–10
The same thing is true in general.
EXAMPLE 3
Find angles in standard position that are coterminal with an angle of
(a) 23p/5 radians
(b) p/12 radians.
t + 2πt
t − 2π
t + 4π
x
y
−
5π
4
432 CHAPTER 6 Trigonometric Functions
x
y
= 2π+ 2π+
16π
3
4π
3
Figure 6–8
Figure 6–9
Coterminal
Angles
Increasing or decreasing the radian measure of an angle by an integer mul-
tiple of 2p results in a coterminal angle.

SOLUTION
(a) We can subtract 2p to obtain a coterminal angle whose measure is
23
5
p
2p
23
5
p
10
5
p
13
5
p
radians,
or we can subtract 4p to obtain a coterminal angle of measure
23
5
p
4p
3
5
p
radians.
Subtracting 6p produces a coterminal angle of
23
5
p
6p
7
5
p
radians.
(b) An angle of
12
p
radians is coterminal with an angle of
1
p
2
2p
2
1
3
2
p
radians
and with an angle of
1
p
2
2p
2
1
5
2
p
radians. ■
RADIAN/DEGREE CONVERSION
Although we shall generally work with radians, it may occasionally be necessary
to convert from radian to degree measure or vice versa. The key to doing this is
the fact that
(
*
) p radians 180°.
Dividing both sides of (
*
) by p shows that
1 radian
1
p
80
degrees 57.3°,
and dividing both sides of (
*
) by 180 shows that
1°
1
p
80
radians .0175 radians.
Consequently, we have these rules.
EXAMPLE 4
Find the degree measure of the angles with radian measure:
(a) 2.4 radians (b) p60 radians (c) .3 radians.
SECTION 6.1 Angles and Their Measurement 433
Radian/Degree
Conversion
To convert radians to degrees, multiply by
1
p
80
.
To convert degrees to radians, multiply by
1
p
80
.

SOLUTION In each case, multiply the given radian measure by
1
p
80
.
(a) 2.4
1
p
80
4
p
32
137.51. (b)
6
p
0
1
p
80
1
6
8
0
0
3.
(c) (.3)
1
p
80
p
54
17.19. ■
EXAMPLE 5
Find the radian measure of the angles with degree measure:
(a) 12 (b) 150 (c) 236
SOLUTION In each case, multiply by
1
p
80
.
(a) 12
1
p
80
1
p
5
radians. (b) 150
1
p
80
6
5p
radians.
(c) 236
1
p
80
5
4
9
5
p
4.12 radians. ■
434 CHAPTER 6 Trigonometric Functions
TECHNOLOGY TIP
If your TI or Casio calculator is in
radian mode, you can convert an angle
from degrees to radians by using in
the menu/submenu listed below.
TI-84: ANGLE
TI-86/89: MATH/ANGLE
Casio: OPTN/ANGLE
For example, keying in 180 and press-
ing ENTER, produces
3.141592654,
the decimal approximation of p.
Similarly, if the calculator is in de-
gree mode, you can convert an angle
from radians to degrees by using r in
the same menu.
To make conversions on HP-39gs,
use DEG RAD or RAD DEG in the
MATH/REAL menu.
EXERCISES 6.1
In Exercises 1–5, find the radian measure of the angle in standard
position formed by rotating the terminal side by the given amount.
1. 1/9 of a circle 2. 1/24 of a circle
3. 1/18 of a circle 4. 1/72 of a circle
5. 1/36 of a circle
6. State the radian measure of every standard position angle in
the figure.*
x
y
5π
6
π 0 (2π)
4π
3
3π
2
7π
4
π
6
π
4
π
2
In Exercises 7–10, estimate the radian measure of the angle.
7. 8.
9. 10.
In Exercises 11–14, find the radian measure of four angles in
standard position that are coterminal with the angle in stan-
dard position whose measure is given.
11. p/4 12. 7p/5
13. p/6 14. 9p/7
In Exercises 15–18, determine whether or not the given angles
in standard position are coterminal.
15.
5
1
p
2
,
1
1
7
2
p
16.
7
6
p
,
5
6
p
17. 117, 837 18. 170, 550
*This is the same diagram that appears in Figure 6–4 on page 430,
showing positive angles in standard position.
SPECIAL TOPICS 6.1.A Arc Length and Angular Speed 435
In Exercises 19–26, find the radian measure of an angle in
standard position that has measure between 0 and 2p and is
coterminal with the angle in standard position whose measure
is given.
19. p/3 20. 3p/4 21. 19p/4
22. 16p/3 23. 7p/5 24. 45p/8
25. 7 26. 18.5
In Exercises 27–38, convert the given degree measure to radians.
27. 6° 28. 10° 29. 12°
30. 36° 31. 75° 32. 105°
33. 135° 34. 165° 35. 225°
36. 252° 37. 930° 38. 585°
In Exercises 39–50, convert the given radian measure to
degrees.
39. p/5 40. p/6 41. p/10
42. 2p/5 43. 3p/4 44. 5p/3
45. p/45 46. p/60 47. 5p/12
48. 7p/15 49. 27p/5 50. 41p/6
In Exercises 51–56, determine the positive radian measure of
the angle that the second hand of a clock traces out in the
given time.
51. 40 seconds 52. 50 seconds
53. 35 seconds 54. 2 minutes and 15 seconds.
55. 3 minutes and 25 seconds 56. 1 minute and 55 seconds
In Exercises 57–64, a wheel is rotating around its axle. Find
the angle (in radians) through which the wheel turns in the
given time when it rotates at the given number of revolutions
per minute (rpm). Assume that t 0 and k 0.
57. 3.5 minutes, 1 rpm 58. t minutes, 1 rpm
59. 1 minute, 2 rpm 60. 3.5 minutes, 2 rpm
61. 4.25 minutes, 5 rpm 62. t minutes, 5 rpm
63. 1 minute, k rpm 64. t minutes, k rpm
6.1.A SPECIAL TOPICS Arc Length and Angular Speed
■ Find the length of an arc intercepted by a given angle.
■ Find the area of a circular sector.
■ Find the linear and angular speeds of an object moving
around a circle.
Consider a circle of radius r and an angle of u radians, as shown in Figure 6–11.
The sides of the angle of u radians determine an arc of length s on the circle. We
say that the central angle of u radians intercepts an arc of length s on the circle
(or that an arc of length s is intercepted by a central angle of u radians).
It can be shown that the ratio of the arc length s to the circumference 2pr of
the entire circle in Figure 6–11 is the same as the ratio of the central angle of u
radians to the full-circle angle of 2p radians; that is,
2p
s
r
2
u
p
.
Solving this equation for s, we obtain the following fact.
Section Objectives
Arc
Length
A central angle of u radians in a circle of radius r intercepts an arc of length
s ur,
that is, the length s of the arc is the product of the radian measure of the
angle and the radius of the circle.
y
r
s
θ
radians
x
Figure 6–11
