Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

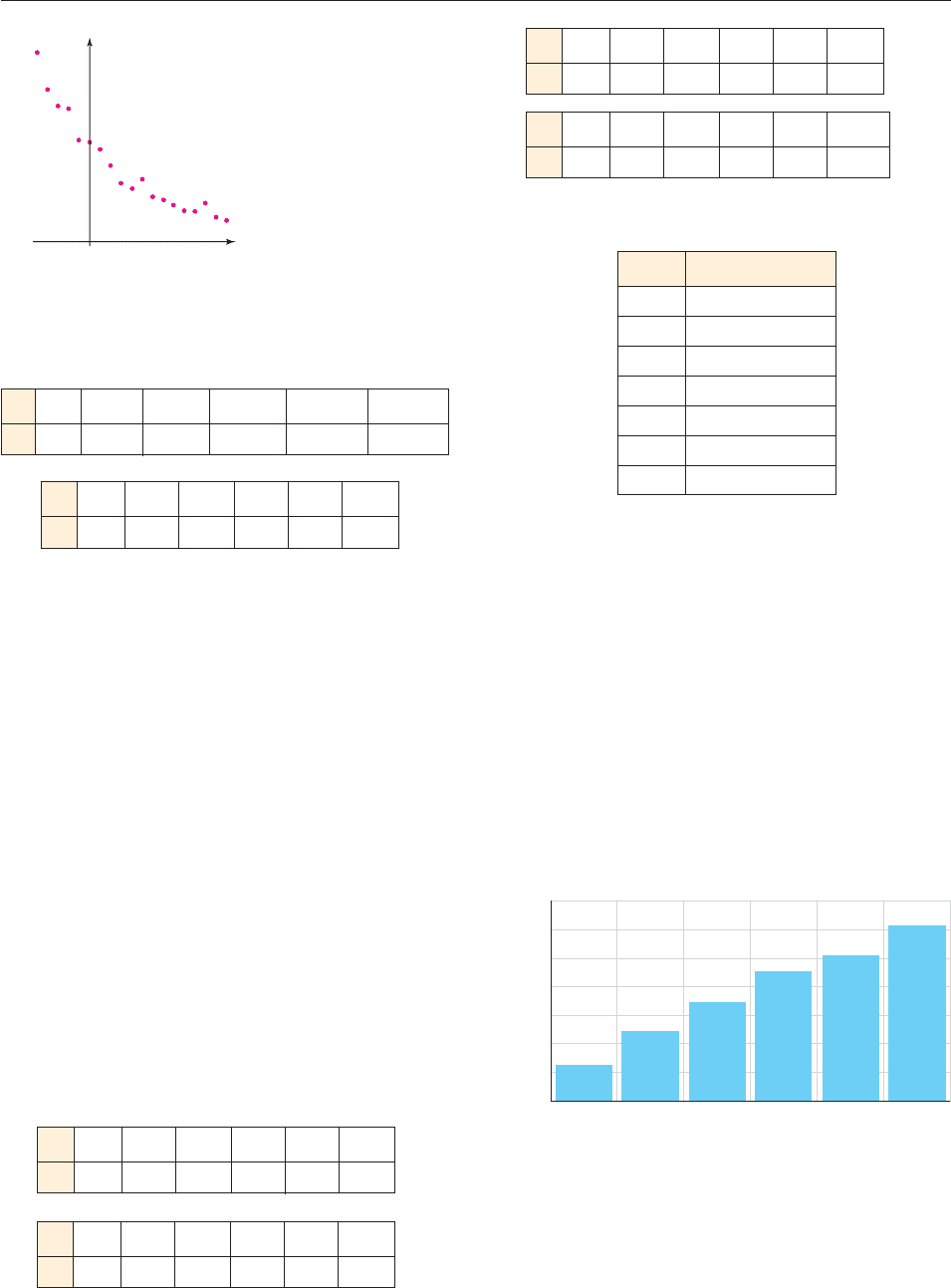
10.
In Exercises 11 and 12, compute the ratios of successive entries
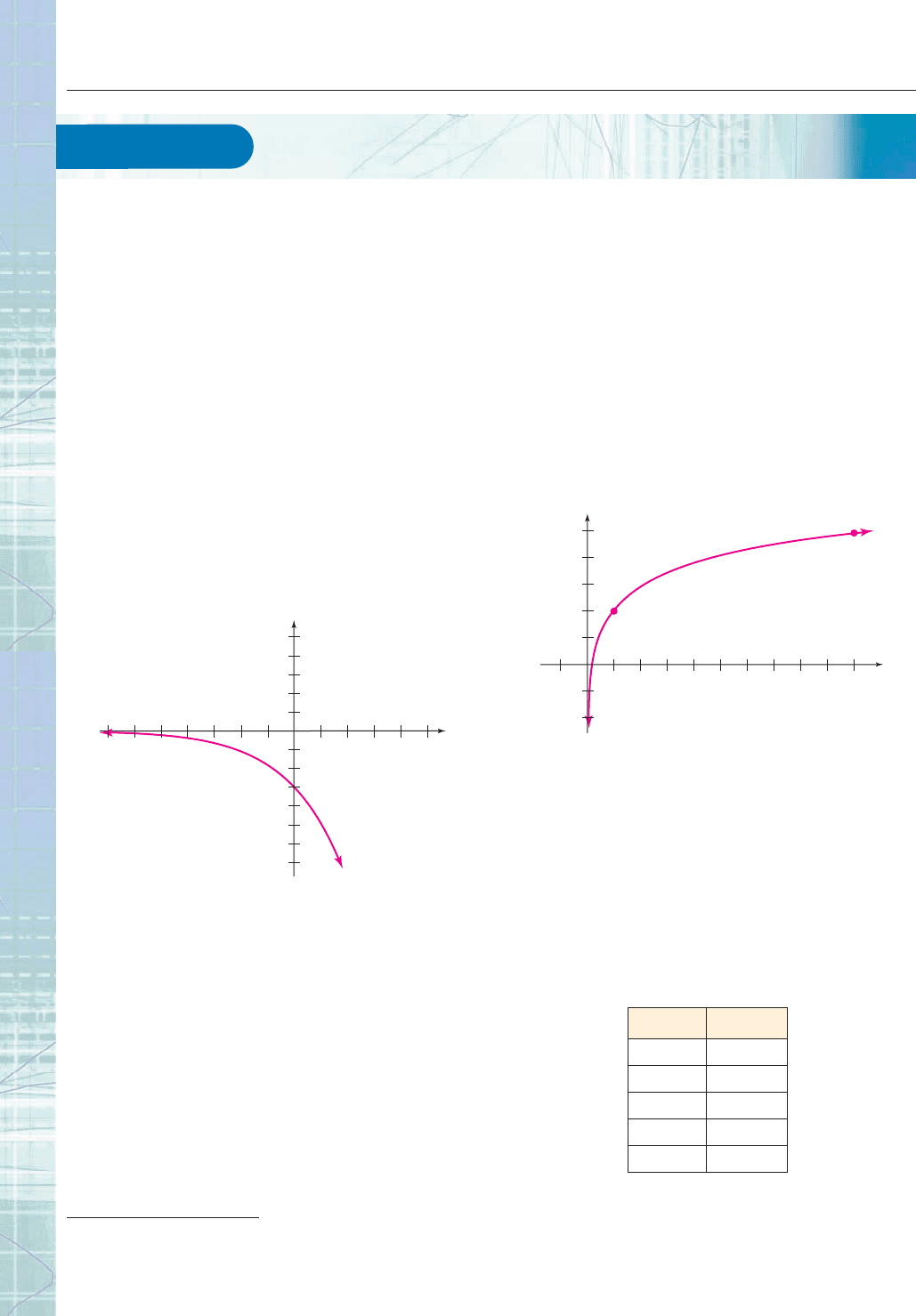
in the table to determine whether or not an exponential model
is appropriate for the data.
11.
12.
13.
(a) Show algebraically that in the logistic model for the
U.S. population in Example 2, the population can never
exceed 442.1 million people.
(b) Confirm your answer in part (a) by graphing the logistic
model in a window that includes the next three centuries.
14. According to estimates by the U.S. Bureau of the Census,
the U.S. population was 287.7 million in 2002. On the basis
of this information, which of the models in Example 2 ap-
pears to be the most accurate predictor?
15. Graph each of the following power functions in a window
with 0 x 20.
(a) f (x) x
1.5
(b) g(x) x
.75
(c) h(x) x
2.4
16. On the basis of your graphs in Exercise 15, describe the
general shape of the graph of y ax
r
when a 0 and
(a) r 0 (b) 0 r 1(c)r 1
In Exercises 17–20, determine whether an exponential, power,
or logarithmic model (or none or several of these) is appropri-
ate for the data by determining which (if any) of the following
sets of points are approximately linear:
{(x, ln y)}, {(ln x, ln y)}, {(ln x, y)}.
where the given data set consists of the points {(x, y)}.
17.
18.
x
y
416 CHAPTER 5 Exponential and Logarithmic Functions
19.
20.
21. The table shows the number of babies born as twins,
triplets, quadruplets, etc., over a 7-year period.
(a) Sketch a scatter plot of the data, with x 1 corresponding
to 1989.
(b) Plot each of the following models on the same screen as
the scatter plot.
f(x) 93,201.973 4,545.977 ln x
g(x)
1
10
.1
2
5
,5
3
1
6
9
e
.9
.
8
4263x
.
(c) Use the table feature to estimate the number of multiple
births in 2000 and 2010.
(d) Over the long run, which model do you think is the bet-
ter predictor?
22. The graph shows the U.S. Census Bureau estimates of future
U.S. population.
(a) How well do the projections in the graph compare with
those given by the logistic model in Example 2?
(b) Find a logistic model of the U.S. population, using the
data given in Example 2 for the years from 1900 to 2000.
(c) How well do the projections in the graph compare with
those given by the model in part (b)?
275
250
300
325
350
375
425
400
2000 2010 2020
Year
U.S. Population Projections: 2000–2050
20302040 2050
Population (in millions)
281.422
308.935
335.805
363.584
377.350
403.687
x 02 4 6 8 10
y 3 15.2 76.9 389.2 1975.5 9975.8
x 13 5 7 9 11
y 3 21 55 105 171 253
x 13 5 7 9 11
y 2 25 81 175 310 497
x 36 9121518
y 385 74 14 2.75 .5 .1
x 510152025 30
y 17 27 35 40 43 48
x 510152025 30
y 2 110 460 1200 2500 4525
Year Multiple Births
1989 92,916
1990 96,893
1991 98,125
1992 99,255
1993 100,613
1994 101,658
1995 101,709
23. Infant mortality rates in the United States are shown in the
table.
(a) Sketch a scatter plot of the data, with x 0 correspond-
ing to 1900.
(b) Verify that the set of points (x, ln y), where (x, y) are the
original data points, is approximately linear.
(c) On the basis of part (b), what type of model would be
appropriate for this data? Find such a model.
24. The number of children who were home schooled in the
United States in selected years is shown in the table.
†
(a) Sketch a scatter plot of the data, with x 0 correspond-
ing to 1980.
(b) Find a quadratic model for the data.
(c) Find a logistic model for the data.
(d) What is the number of home-schooled children pre-
dicted by each model for the year 2015?
(e) What are the limitations of each model?
25. The average number of students per computer in the U.S.
public schools (elementary through high school) is shown
in the table at the top of the next column.
SECTION 5.6 Exponential, Logarithmic, and Other Models 417
(a) Sketch a scatter plot of the data, with x 7 correspon-
ding to 1987.
(b) Find an exponential model for the data.
(c) Use the model to estimate the number of students per
computer in 2015.
(d) In what year, according to this model, will each student
have his or her own computer in school?
(e) What are the limitations of this model?
26. (a) Find an exponential model for the federal debt, based
on the data in the table.* Let x 0 correspond to 1960.
(b) Use the model to estimate the federal debt in 2010.
Infant
Mortality
Year Rate
*
1920 76.7
1930 60.4
1940 47.0
1950 29.2
1960 26.0
1970 20.0
1980 12.6
Infant
Mortality
Year Rate
*
1985 10.6
1990 9.2
1995 7.6
2000 6.9
2001 6.8
2002 7.0
2003 6.9
*Rates are infant (under 1 year) deaths per 1000 live births.
†
National Home Education Research Institute
Fall of Number of
School Year Children (in thousands)
1985 183
1988 225
1990 301
1992 470
1993 588
1994 735
1995 800
1996 920
1997 1100
1999 1400
2000 1700
2005 1900
Fall of
School Year Students/Computer
1987 32
1988 25
1989 22
1990 20
1991 18
1992 16
1993 14
1994 10.5
1995 10
1996 7.8
1997 6.1
1998 5.7
1999 5.4
2000 5
2002 4.9
2003 4.8
GROSS FEDERAL DEBT
End of Amount
Fiscal Year (in billions of dollars)
1960 290.5
1965 322.3
1970 380.9
1975 541.9
1980 909.0
1985 1817.4
1990 3206.3
1995 4920.6
2000 5628.7
2005 8031.4
†
*http//:www.whitehouse.gov/omb/budget/fy2006/pdf/hist.pdf
(pages 118–119)
†
Estimated
2000 1,316,333
2001 1,330,007
2002 1,367,547
2003 1,392,796
2004 1,421,911
27. The number of U.S. adults on probation from 2000 to 2004
is shown in the first two columns of the following table.*
(a) Sketch a scatter plot of the data with x 0 correspon-
ding to 2000.
(b) Fill in column 4 by dividing each entry in column 2 by
the preceding one; round your answers to two decimal
places. In view of column 4, what type of model is ap-
propriate here?
(c) Find an appropriate model for the data.
(d) Use the model to complete column 3 in the table. How
well does the model fit the data?
(e) If the model remains accurate, how many adults will be
on probation in 2010?
28. In the past two decades, more women than men have been
entering college. The table shows the percentage of male
first-year college students in selected years.
†
(a) Find three models for this data: exponential, logarith-
mic, and power, with x 5 corresponding to 1985.
(b) For the years 1985–2005, is there any significant differ-
ence among the models?
(c) Assume that the models remain accurate. What year
does each predict as the first year in which fewer than
43% of first-year college students will be male?
(d) We actually have some additional data:
Which model did the best job of predicting the new
data?
418 CHAPTER 5 Exponential and Logarithmic Functions
29. The table gives the life expectancy (at birth) of a woman
born in the given year.*
(a) Find a logarithmic model for the data, with x 10 cor-
responding to 1910.
(b) Use the model to find the life expectancy of a woman
born in 1996. [For comparison, the actual expectancy is
79.1 years.]
(c) Assume that the model remains accurate. In what year
will the life expectancy of a woman born in that year be
at least 83 years?
30. The table gives the death rate in motor vehicle accidents
(per 100,000 population) in selected years.
(a) Find an exponential model for the data, with x 0 cor-
responding to 1970.
(b) What was the death rate in 1998 and in 2002?
(c) Assume that the model remains accurate, when will the
death rate drop to 13 per 100,000?
Ratio
Adults on Predicted Number of
Year Probation Adults on Probation
Year 1985 1990 1995 1997 1998 1999 2003 2004 2005
Percent 48.9 46.9 45.6 45.5 45.5 45.3 45.1 44.9 45.0
Year 1970 1980 1985 1990 1995 2000 2003
Death Rate 26.8 23.4 19.3 18.8 16.5 15.6 15.4
*Statistical Abstract of the United States.
†Higher Education Research Institute at UCLA.
Year Life Expectancy (in years)
1910 51.8
1930 61.6
1950 71.1
1970 74.7
1990 78.8
1995 78.9
1997 79.4
1999 79.4
2000 79.7
2001 79.8
2002 79.9
2003 80.1
*National Center for Health Statistics.
Year 2000 2001 2002 2006
Percent 45.2 44.9 45.0 45.1

CHAPTER 5 Review 419
Chapter 5 Review
IMPORTANT CONCEPTS
Section 5.1
nth root 342
Principal nth root 343
Rational exponents 344
Exponent Laws 345
Radical notation 346
Rationalizing numerators and
denominators 347
Irrational exponents 348
Special Topics 5.1.A
Power Principle 350
Section 5.2
Exponential functions 358–359
Exponential growth and decay 361–362
The number e 363
Special Topics 5.2.A
Compound interest formula 369
Continuous compounding 373
Section 5.3
Common logarithmic functions 376
Natural logarithmic functions 378
Properties of logarithms 380
Section 5.4
Product Law for Logarithms 385
Quotient Law for Logarithms 387
Power Law for Logarithms 388
Richter scale 390
Special Topics 5.4.A
Logarithmic functions to base b 393
Properties of logarithms 394
Logarithm Laws 395
Change of base formula 397
Section 5.5
Exponential equations 399
Logarithmic equations 403
Section 5.6
Exponential, logarithmic, power, and
logistic models 409
IMPORTANT FACTS & FORMULAS
■ Laws of Exponents:
c
r
c
s
c
rs
(cd)
r
c
r
d
r
c
c
r
s
c
rs
d
c
r
d
c
r
r
(c
r
)
s
c
rs
c
r
c
1
r
■ g(x) log x is the inverse function of f (x) 10
x
:
10
log v
v for all v 0 and log 10
u
u for all u.
■ g(x) ln x is the inverse function of f (x) e
x
:
e
ln v
v for all v 0 and ln (e
u
) u for all u.
■ h(x) log
b
x is the inverse function of k(x) b
x
:
b
log
b
v
v for all v 0 and log
b
(b
u
) u for all u.
■ Logarithm Laws: For all v, w 0 and any k:
ln (vw) ln v ln w log
b
(vw) log
b
v log
b
w
ln
w
v
ln v ln w log
b
w
v
log
b
v log
b
w
ln (v
k
) k(ln v) log
b
(v
k
) k(log
b
v)
420 CHAPTER 5 Exponential and Logarithmic Functions
■ Exponential Growth Functions:
f (x) P(1 r)
x
(0 r 1),
f (x) Pa
x
(a 1),
f (x) Pe
kx
(k 0)
■ Exponential Decay Functions:
f (x) P(1 r)
x
(0 r 1),
f (x) Pa
x
(0 a 1),
f (x) Pe
kx
(k 0)
■ Compound Interest Formula: A P(1 r)
t
■ Change of Base Formula: log
b
v
l
l
n
n
b
v
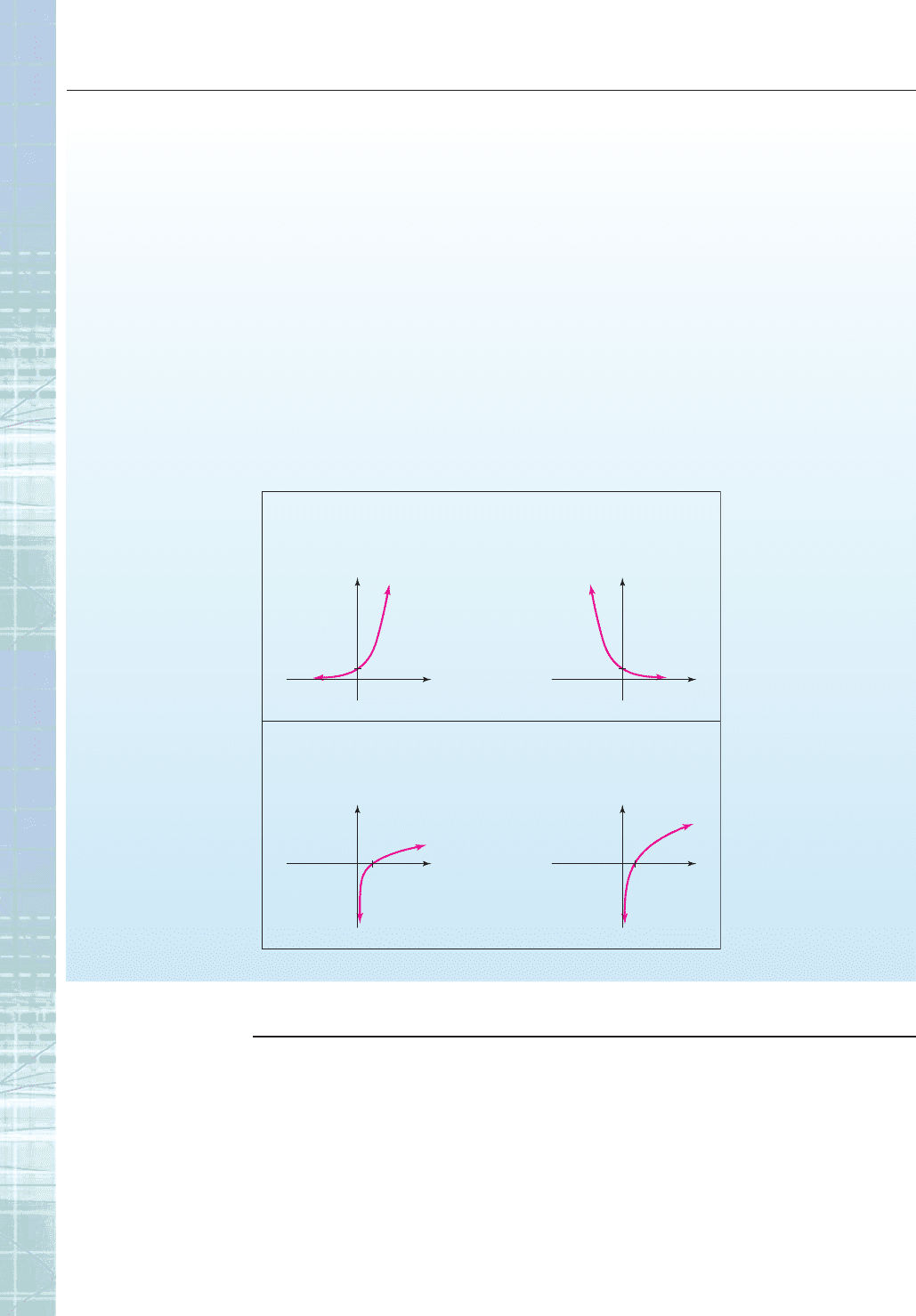
CATALOG OF BASIC FUNCTIONS—PART 3
f(x) = b
x
(b > 1) f(x) = b
x
(0 < b < 1)
Exponential Functions
f(x) = log x
1
1
f(x) = ln x
Logarithmic Functions
x
y
x
y
x
y
x
y
1
1
In Questions 1–6, simplify the expression.
1.
5
a
20
2. (
4
5
a
2
b)
4
(a
3
b
)
2
3. (x
2/5
y
2/3
)(x
2/3
y
4
)
1/2
4.
5. (x
1/3
y
1/3
)(x
1/3
y
1/3
) 6. 2a
3/5
(5a
7/5
4a
3/5
)
(2x)
1/3
(2y)
3
(9x)
1/2
(3x)
2/3
(3y)
2
x
5/2
In Exercises 7 and 8, simplify and write the expression without
radicals or negative exponents:
7. 8.
(9x
4
)
1/
3
3
x
3
9
2
x
5
9. Rationalize the numerator and simplify:
3x 3
h 5
3x 5
h
3
7x
4
y
1
1
3
56x
2
y
2
REVIEW QUESTIONS

10. Rationalize the denominator:
2x
6
8
In Questions 11–16, find all real solutions of the equation.
11. 2x 1
3x 4 12.
3
9 y
2
3
13. 3 x 3
5x 1
2
14. x
2/3
3x
1/3
18 0
15.
3
x
4
2
x
3
6
x 7
x 3
16. x
4/3
x 2x
2/3
x
1/3
4
In Questions 17 and 18, find a viewing window (or windows)
that shows a complete graph of the function.
17. f (x) 2
x
3
x2
18. g(x) ln
x
x
2
In Questions 19–22, sketch a complete graph of the function.
Indicate all asymptotes clearly.
19. g(x) 2
x
1 20. f(x) 2
x1
21. h(x) ln (x 4) 2 22. k(x) ln
x
x
4
23. A computer software company claims the following func-
tion models the “learning curve” for their mathematical
software.
P(t)
1 4
1
8
0
.2
0
e
.52t
,
where t is measured in months and P(t) is the average per-
cent of the software program’s capabilities mastered after
t months.
(a) Initially, what percent of the program is mastered?
(b) After six months, what percent of the program is mas-
tered?
(c) Roughly, when can a person expect to “learn the most in
the least amount of time”?
(d) If the company’s claim is true, how many months will it
take to have completely mastered the program?
24. Compunote has offered you a starting salary of $60,000
with $1000 yearly raises. Calcuplay offers you an initial
salary of $30,000 and a guaranteed 6% raise each year.
(a) Complete the following table for each company.
(b) For each company, write a function that gives your
salary in terms of years employed.
CHAPTER 5 Review 421
(c) If you plan on staying with the company for only five
years, which job should you take to earn the most
money?
(d) In what year does the salary at Calcuplay exceed the
salary at Compunote?
In Questions 25–30, translate the given exponential statement
into an equivalent logarithmic one.
25. e
3.14
23 26.
e
1.8
2
0001
3
27. e
x7y
4a b 28. e
2a
2
9
3.16
29. 10
2.248
177 30. 10
4x1
y
In Questions 31–36, translate the given logarithmic statement
into an equivalent exponential one.
31. ln 404 6.0014 32. ln (3x 2y) b
33. ln (4xy) 15t 34. log 3675 3.565258
35. log
6
(3x 4) y 36. log
a
(uv) w
2
In Questions 37–40, evaluate the given expression without
using a calculator.
37. ln e
2/3
38. ln
4
e
5
39. e
ln (x/2)
40. e
3ln (3x
2
7y)
41. Simplify: 4 ln
5
x
(1/5)ln x
42. Simplify: ln (e
5e
2
)
2
4e
2
In Questions 43–45, write the given expression as a single
logarithm.
43. ln 6a 4 ln b ln 2a
44. log
4
16x
2
2 log
4
y 2
45. 3 ln x 4(ln x
3
5 ln x)
46. log (.001) ?
47. log
30
900 ?
48. You are conducting an experiment about memory. The peo-
ple who participate agree to take a test at the end of your
course and every month thereafter for a period of two
years. The average score for the group is given by the
model
M(t) 91 14 ln (t 1) (0 t 24)
where t is time in months after the first test.
(a) What is the average score on the initial exam?
(b) What is the average score after three months?
(c) When will the average drop below 50%?
(d) Is the magnitude of the rate of memory loss greater in
the first month after the course (from t 0 to t 1) or
after the first year (from t 12 to t 13)?
(e) Hypothetically, if the model could be extended past t
24 months, would it be possible for the average score to
be 0%?
Year Compunote
1 $60,000
2 $61,000
3
4
5
Year Calcuplay
1 $30,000
2 $31,800
3
4
5

422 CHAPTER 5 Exponential and Logarithmic Functions
49. Which of the following statements are true?
(a) ln 10 (ln 2)(ln 5) (b) ln (e/6) ln e ln 6
(c) ln (1/7) ln 7 0 (d) ln (e) 1
(e) None of the above is true.
50. Which of the following statements are false?
(a) 10 (log 5) log 50 (b) log 100 3 log 10
5
(c) log 1 ln 1 (d) log 6/log 3 log 2
(e) All of the above are false.
Use the following six graphs for Questions 51 and 52.
1
−1
2
12
x
y
IV
1
−1
−1
2
1
x
y
III
1
−1
−1
2
3
1
x
y
II
1
−1
−1
2
3
I
1
x
y
51. If b 1, then the graph of f (x) log
b
x could possibly be:
(a) I (b) IV
(c) V (d) VI
(e) none of these
52. If 0 b 1, then the graph of g(x) b
x
1 could possi-
bly be:
(a) II (b) III
(c) IV (d) VI
(e) none of these
53. If log
4
16
5x
2
160, then what is x?
54. What is the domain of the function f (x) ln
x
2
x
1
?
In Questions 55–63, solve the equation for x.
55. 9
9x
3
x
2
5x
56. e
5x
14
57. 2
27
x
7 19/3 58. 248e
3x
620
59. 2a 3b c ln x 60. 4
x
5
2x1
61. ln 5x ln (2x 4) ln 30
62. ln (2x 5) ln 4x 2
63. log (4x
2
9) 2 log (2x 3)
64. At a small community college the spread of a rumor through
the population of 500 faculty and students can be modeled
by.
ln (n) ln (1000 2n) .65t ln 998,
where n is the number of people who have heard the rumor
after t days.
(a) How many people know the rumor initially? (at t 0)
(b) How many people have heard the rumor after four days?
1
−1
−2
−1−2
12
x
y
VI
1
−1
12
x
y
V
CHAPTER 5 Review 423
(c) Roughly, in how many weeks will the entire population
have heard the rumor?
(d) Use the properties of logarithms to write n as a function
of t; in other words solve the model above for n in terms
of t.
(e) Enter the function you found in part (d) into your calcu-
lator and use the table feature to check your answers to
parts (a), (b), and (c). Do they agree?
(f ) Now graph the function. Roughly over what time inter-
val does the rumor seem to “spread” the fastest?
65. The half-life of polonium (
210
Po) is 140 days. If you start
with 10 milligrams, how much will be left at the end of a
year?
66. An insect colony grows exponentially from 100 to 1500 in
2 months time. If this growth pattern continues, how long
will it take the insect population to reach 100,000?
67. Hydrogen-3 decays at a rate of 5.59% per year. Find its
half-life.
68. The half-life of radium-88 is 1590 years. How long will it
take for 10 grams to decay to 1 gram?
69. How much money should be invested at 4.5% per year,
compounded quarterly, in order to have $5000 in 6 years?
70. At what annual rate should you invest your money if you
want it to triple in 20 years (assume continuous com-
pounding)?
71. One earthquake measures 4.6 on the Richter scale. A second
earthquake is 1000 times more intense than the first. What
does it measure on the Richter scale?
72. The table gives the population of Austin, Texas.*
73. The wind-chill factor is the temperature that would produce
the same cooling effect on a person’s skin if there were no
wind. The table shows the wind-chill factors for various
wind speeds when the temperature is 25°F.*
(a) What does a 20-mph wind make 25°F feel like?
(b) Sketch a scatter plot of the data.
(c) Explain why an exponential model would be appro-
priate.
(d) Find an exponential model for the data.
(e) According to the model, what is the wind-chill factor
for a 23-mph wind?
74. Cigarette consumption in the United States has been de-
creasing for some time, as shown in the table (in which the
number of cigarettes each year is in billions).
†
(a) Let x 10 correspond to 1995 and find exponential,
logarithmic, and power models for the data.
(b) Which of the three models do you think is most appro-
priate? Justify your answer.
(c) If you were a doctor, which model would you prefer for
the future? Which one would you prefer if you manufac-
tured cigarettes?
Year Population
1950 132,459
1970 253,539
1980 345,890
1990 465,622
2000 656,562
*U.S. Census Bureau.
(a) Sketch a scatter plot of the data, with x 0 correspon-
ding to 1950.
(b) Find an exponential model for the data.
(c) Use the model to estimate the population of Austin in
1960 and 2005.
(d) It turns out that the 2004 population is 681,804. If we
wanted to estimate the 2009 population, should we
refine our exponential model, or should we decide that
an exponential model isn’t a good one? Why or why
not?
Wind Chill
Wind Speed (mph) Temperature (in °F)
025
519
10 15
15 13
20 11
25 9
30 8
35 7
40 6
45 5
*National Weather Service.
†
U.S. Dept. of Agriculture.
Year Cigarettes
2000 565
2001 562
2002 532
2003 499
2004 494
2005 489
424 CHAPTER 5 Exponential and Logarithmic Functions
Chapter
5
Test
Sections 5.1 and 5.2; Special Topics 5.1.A
and 5.2.A
1. Rationalize the denominator. Assume all constants are pos-
itive, real numbers.
(a)
2
1
h
(b)
a
a
b
b
(a b)
(c)
x
3
4
2. Find all real solutions of each equation.
(a)
x
3
x
2
4x
5
x 1
(b) (x 1)
2/3
4
3. A population grows at the rate P P
0
e
.01t
where t is in
years, and P
0
is a positive constant.
(a) When t 10, the population is 1,000. Find P
0
.
(b) Use your answer to part (a) to find the initial population.
(c) Use your answer to part (a) to find the population when
t 20.
4. The following is a graph of y Ae
kt
(a) Is k positive or negative? How do you know?
(b) Find the value of A
5. Simplify the following expressions. Assume all constants
are positive, real numbers.
(a)
10
5
75
(b)
3ab
2
a
3
a
4
b
7
(c)
a
1/2
(
b
a
3
1
/2
/2
b
5/2
)
6. In 1965, Gordon Moore (a cofounder of Intel) observed that
the amount of computing power possible to put on a chip dou-
bles every two years.* In 1990 there were about 1,000,000
transistors per chip. Assuming that Moore’s law is true:
(a) How many transistors per chip were there in 2000?
(b) How many were there in 1985?
(c) How many will there be in 2020?
−4
−5
−3
−6
−7
21
0
453
−2 −1−3−4−5−6−7
−1
−2
2
4
3
1
5
x
y
7. How much money will be in a savings account after one
year if the initial deposit is $3000 and the interest rate is
8% compounded quarterly?
Sections 5.3–5.6; Special Topics 5.4.A
8. (a) log
5
625 (b) 11
log
11
(xh)
(c) log
3
(9
1138
)
9. The half-life of Carbon 14 is 5730 years. If a sample of bone
has lost 10% of its original C-14, roughly how old is the bone?
10. Simplify the following expressions
(a) ln(e
x
2
y
2
) (b) e
ln(a)2ln(b)
(c) ln
3
1
e
11. The following is a graph of y A log(x) B. Find A and B.
12. Simplify the following expressions, if possible. Assume all
constants are positive real numbers
(a)
ln(x
l
)
n
(ax
l
)
n(a)
(b) ln
b
2
4
4 ln(b)
(c) ln(3 x
2
)
13. A population of mayflies grows according to the equation
P 230e
.6t
where t is in days.
(a) How many mayflies were there initially?
(b) ln how many days will there be 10,000 mayflies?
14. The following data show Madison’s average score at the
game of Fizzbin:
(a) Find a logarithmic model (y a b ln x) for the data
(b) What does the model predict her score was for
February? What will it be in December?
76
0
910821453
−1
−1
−2
2
4
3
1
5
x
y
*Intel Corporation.
Month Score
January 120.00
March 136.48
April 140.79
May 144.14
June 146.88

425
Greg Pease/Getty Images
DISCOVERY PROJECT 5 Exponential and Logistic Modeling
of Diseases
Diseases that are contagious and are transmitted homogeneously through a popu-
lation often appear to be spreading exponentially. That is, the rate of spread is pro-
portional to the number of people in the population who are already infected. This
is a reasonable model as long as the number of infected people is relatively small
in comparison with the number of people in the population who can be infected.
The standard exponential model looks like this:
f (t) Y
0
e
rt
.
Y
0
is the initial number of infected people (the number on the arbitrarily decided
day 0), and r is the rate by which the disease spreads through the population. If the
time t is measured in days, then r is the ratio of new infections to current infec-
tions each day.
Suppose that in Big City, population 3855, there is an outbreak of dingbat dis-
ease. On the first Monday after the outbreak was discovered (day 0), 72 people
have dingbat disease. On the following Monday (day 7), 193 people have dingbat
disease.
1. Using the exponential model, Y
0
is clearly 72. Calculate the value of r.
2. Using your values of Y
0
and r, predict the number of cases of dingbat
disease that will be reported on day 14.
It turns out that eventually, the spread of disease must slow as the number of in-
fected people approaches the number of susceptible people. What happens is that
some of the people to whom the disease would spread are already infected. As
time goes on, the spread of the disease becomes proportional to the number of sus-
ceptible and uninfected people. The disease then follows the logistic model:
g(t) .
Y
0
is still the initial value, and r serves the same function as before, at least at the
initial time. The extra parameter a is not so obvious, but it is inversely related to
the number of people susceptible to the disease. Unfortunately, the algebra to
solve for a is quite complicated. It is much easier to approximate a using the same
r from the exponential model.
3. On day 14 in Big City, 481 people have dingbat disease. Using the val-
ues of Y
0
and r from Exercise 1 in the rule of the function g, determine
the value of a. [Hint: g(14) 481.] Does g overestimate or underesti-
mate the number of people with dingbat disease on day 7?
4. Use the function g from Exercise 3 to approximate the number of people
in Big City who are susceptible to the disease. Does this model make
sense? [Remember, as time goes on, the number of people infected ap-
proaches the number of people susceptible.]
rY
0
aY
0
(r aY
0
)e
rt
