Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


We have
log v log 10
2
2 and log w log 10
3
3,
so that
log v log w 2 3 5.
We also have
log vw log(10
2
10
3
)
log(10
5
) 5.
Hence, log vw log v log w in this case.
Here is the formal proof of the Product Law for natural logarithms.
Proof According to Property 4 of logarithms (in the box on page 380),
e
ln v
v and e
ln w
w.
Therefore, by the first law of exponents (with m ln v and n ln w),
vw e
ln v
e
ln w
e
ln vln w
.
So raising e to the exponent (ln v ln w) produces vw. But the definition of
logarithm says that ln vw is the exponent to which e must be raised to produce
vw. Therefore, we must have ln vw ln v ln w. A similar argument works for
common logarithms. ■
EXAMPLE 1
A calculator shows that ln 7 1.9459 and ln 9 2.1972. Therefore,
ln 63 ln (7
9) ln 7 ln 9 1.9459 2.1972 4.1341. ■
EXAMPLE 2
Use the Product Law to write
(a) log (7xy) as a sum of three logarithms.
(b) log x
2
log y 1 as a single logarithm.
SOLUTION
(a) log (7xy) log 7x log y log 7 log x log y
(b) Note that log 10 1 (why?). Hence,
log x
2
log y 1 log x
2
log y log 10
log (x
2
y) log 10
log (10x
2
y). ■
386 CHAPTER 5 Exponential and Logarithmic Functions
We know that 5
7 35. Key in LOG(35) ENTER. Then key in LOG(5) LOG(7)
ENTER. The answers are the same by the Product Law. Do you get the same answer
if you key in LOG(5) LOG(7) ENTER?
CALCULATOR EXPLORATION
EXAMPLE 3
If a population of cells grows by a factor of ten every year, what do we know
about the common logarithm of the population?
SOLUTION Assume the population is P. Then, next year, the population will
be 10P. The logarithm of the population will be
log (10P) log (10) log (P)
1 log (P).
So the logarithm of the population will increase by one every year. ■
The second law of exponents, namely, b
m
/b
n
b
mn
, may be roughly stated
in words as follows.
The exponent of the quotient is the difference of exponents.
When the exponents are logarithms, this says
The logarithm of a quotient is the difference of the logarithms.
In other words,
The proof of the Quotient Law is very similar to the proof of the Product Law (see
Exercise 27).
EXAMPLE 4
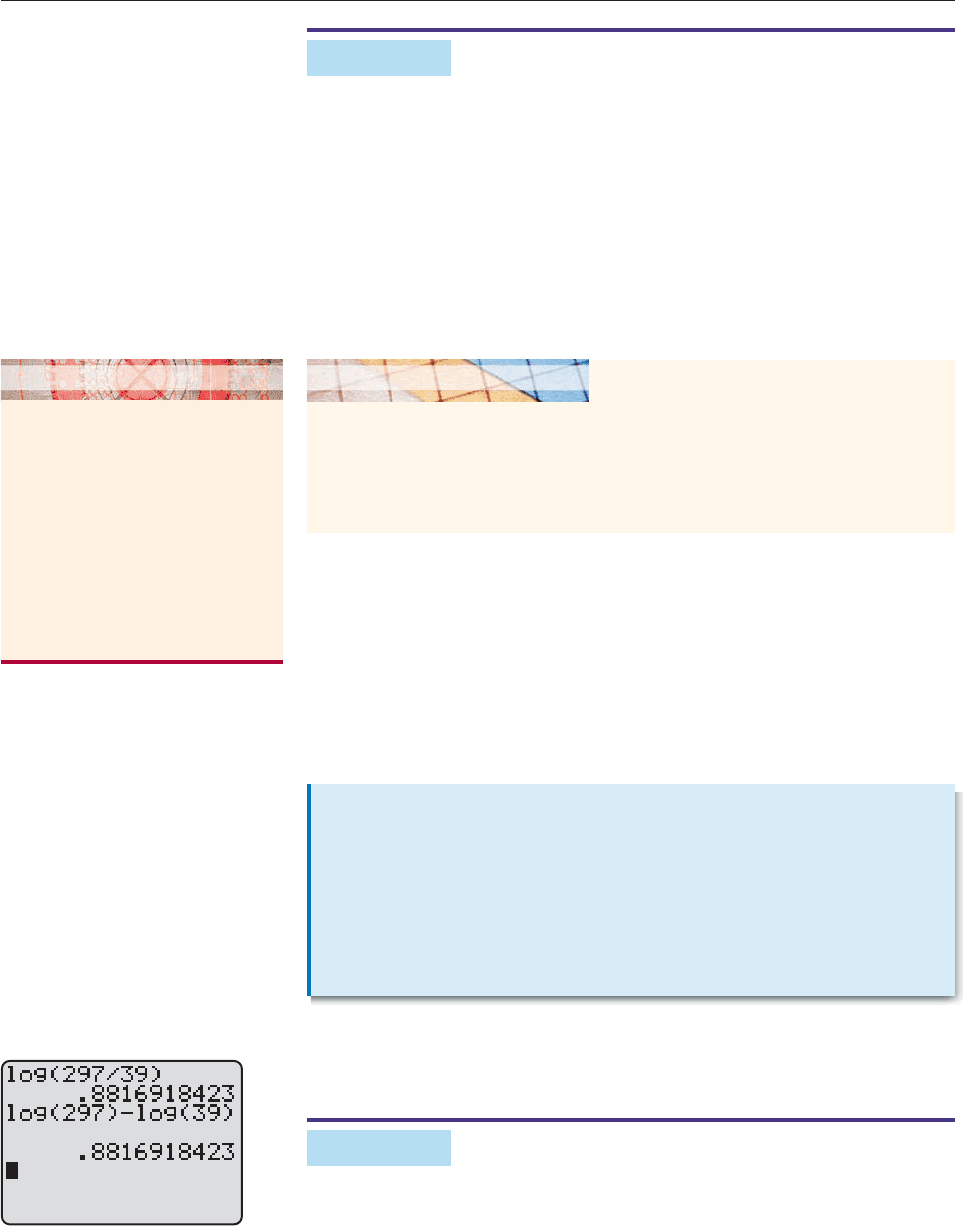
Figure 5–25 illustrates the Quotient Law by showing that
log
2
3
9
9
7
log 297 log 39. ■
SECTION 5.4 Properties of Logarithms 387
Illustrate the Caution in the margin graphically by graphing both
f(x) ln x ln 9 and g(x) ln (x 9)
in the standard viewing window and verifying that the graphs are not the same. In
particular, the functions have different values at x 7.
GRAPHING EXPLORATION
CAUTION
A common error in applying the Product
Law for Logarithms is to write the false
statement
ln 7 ln 9 ln (7 9)
ln 16
instead of the correct statement
ln 7 ln 9 ln (7
9)
ln 63.
Quotient Law
for Logarithms
For all v, w 0,
ln
w
v
ln v ln w
and
log
w
v
log v log w.
Figure 5–25

EXAMPLE 5
For any w 0.
ln
w
1
ln 1 ln w 0 ln w ln w
and
log
w
1
log 1 log w 0 log w log w. ■
The third law of exponents, namely, (b
m
)
k
b
mk
, can also be translated into
logarithmic language.
Proof Since v 10
log v
(why?), the third law of exponents (with b 10 and
m log v) shows that
v
k
(10
log v
)
k
10
(log v)k
10
k(log v)
.
So raising 10 to the exponent k(log v) produces v
k
. But the exponent to which
10 must be raised to produce v
k
is, by definition, log (v
k
). Therefore,
log (v
k
) k(log v), and the proof is complete. A similar argument with e in place
of 10 and “ln” in place of “log” works for natural logarithms. ■
EXAMPLE 6
Express ln 19 without radicals or exponents.
SOLUTION First write 19 in exponent notation, then use the Power Law:
ln 19 ln 19
1/2
1
2
ln 19 or
ln
2
19
. ■
388 CHAPTER 5 Exponential and Logarithmic Functions
CAUTION
Do not confuse ln
w
v
with the quotient
l
l
n
n
w
v
. They are different numbers. For example,
ln
3
3
6
ln (12) 2.4849, but
ln
ln
3
3
6
3
1
.
.
5
0
8
9
3
8
5
6
3.2619.
Power Law
for Logarithms
For all k and all v 0,
ln (v
k
) k(ln v)
and
log (v
k
) k(log v).
GRAPHING EXPLORATION
Illustrate the Caution graphically
by graphing both f (x) ln (x/3)
and g(x) (ln x)/(ln 3) and veri-
fying that the graphs are not the
same at x 36.

EXAMPLE 7
Express as a single logarithm:
log(x
3
2
1)
log x.
SOLUTION
log(x
3
2
1)
log x
1
3
log (x
2
1) log x
log (x
2
1)
1/3
log x [Power Law]
log
3
x
2
1
log x
log
3
x
2
x
1
[Quotient Law] ■
EXAMPLE 8
Express as a single logarithm: ln 3x 4 ln x ln 3xy.
SOLUTION
ln 3x 4
ln x ln 3xy ln 3x ln x
4
ln 3xy [Power Law]
ln (3x
x
4
) ln 3xy [Product Law]
ln
3
3
x
x
y
5
[Quotient Law]
ln
x
y
4
[Cancel 3x] ■
EXAMPLE 9
Simplify: ln
x
x
ln
4
ex
2
.
SOLUTION Begin by changing to exponential notation.
ln
x
1
x
/2
ln (ex
2
)
1/4
ln (x
1/2
) ln (ex
2
)
1/4
1
2
ln x
1
4
ln ex
2
[Power Law]
1
2
ln x
1
4
(ln e ln x
2
) [Product Law]
1
2
ln x
1
4
(ln e 2
ln x) [Power Law]
1
2
ln x
1
4
ln e
1
2
ln x
1
4
ln e
1
4
[ln e 1] ■
SECTION 5.4 Properties of Logarithms 389

APPLICATIONS
Because logarithmic growth is slow, measurements on a logarithmic scale (that is,
on a scale determined by a logarithmic function) can sometimes be deceptive.
EXAMPLE 10
Earthquakes The magnitude R(i) of an earthquake on the Richter scale is given
by R(i) log(i/i
0
), where i is the amplitude of the ground motion of the earth-
quake and i
0
is the amplitude of the ground motion of the so-called zero earth-
quake.* A moderate earthquake might have 1000 times the ground motion of the
zero earthquake (that is, i 1000i
0
). So its magnitude would be
log (1000i
0
/i
0
) log 1000 log 10
3
3.
An earthquake with 10 times this ground motion (that is, i 10
1000i
0
10,000i
0
) would have a magnitude of
log (10,000i
0
/i
0
) log 10,000 log 10
4
4.
So a tenfold increase in ground motion produces only a one-point change on the
Richter scale. In general,
Increasing the ground motion by a factor of 10
k
increases
the Richter magnitude by k units.
†
For instance, the 1989 World Series earthquake in San Francisco measured 7.0 on
the Richter scale, and the great earthquake of 1906 measured 8.3. The difference
of 1.3 points means that the 1906 quake was 10
1.3
20 times more intense than
the 1989 one in terms of ground motion. ■
390 CHAPTER 5 Exponential and Logarithmic Functions
*The zero earthquake has ground motion amplitude of less than 1 micron on a standard seismograph
100 kilometers from the epicenter.
†
Proof: If one quake has ground motion amplitude i and the other 10
k
i, then
R(10
k
i) log (10
k
i/i
0
) log 10
k
log (i/i
0
)
k log (i/i
0
) k R(i).
EXERCISES 5.4
In Exercises 1–10, write the given expression as a single
logarithm.
1. ln x
2
3 ln y
2. 5(ln x) ln 4y ln 3z
3. log (x
2
9) log (x 3)
4. 3(log 2x) 4[log x log (y 5)]
5. 2(ln x) 3(ln x
2
ln x)
6. log
3
2
x
log
5x
7. 3 ln(e
2
e) 3
8. 3 log(7) 4
9. log (10x) log (20y) 1
10. ln (e
3
x
2
) ln (ey
3
) 2
In Exercises 11–16, let u ln x and v ln y. Write the given
expression in terms of u and v. For example,
ln x
3
y ln x
3
ln y 3 ln x ln y 3u v.
11. ln (x
2
y
5
) 12. ln (x
4
y
3
)
13. ln (x
y
2
) 14. ln
15. ln
(
3
x
2
y
)
16. ln
3
x
2
y
2
x
5
xy
y
2

SECTION 5.4 Properties of Logarithms 391
In Exercises 17–23, use graphical or algebraic means to deter-
mine whether the statement is true or false.
17. ln x ln x?
18. ln
1
x
ln
1
x
?
19. log x
5
5(log x)?
20. e
x ln x
x
x
(x 0)?
21. ln x
3
(ln x)
3
?
22. log x
log x
?
23. ln (x 5) ln(x) ln 5?
In Exercises 24 and 25, find values of a and b for which the
statement is false.
24.
l
l
o
o
g
g
a
b
log
a
b
25. log (a b) log a log b
26. If ln b
10
10, what is b?
27. Prove the Quotient Law for Logarithms: For v, w 0,
ln
w
v
ln v ln w. (Use properties of exponents and
the fact that v e
ln v
and w e
ln w
.)
In Exercises 28–31, state the magnitude on the Richter scale of
an earthquake that satisfies the given condition.
28. 100 times stronger than the zero quake.
29. 10
4.7
times stronger than the zero quake.
30. 250 times stronger than the zero quake.
31. 1500 times stronger than the zero quake.
Exercises 32–35 deal with the energy intensity i of a sound,
which is related to the loudness of the sound by the function
L(i) 10
log (i/i
0
), where i
0
is the minimum intensity de-
tectable by the human ear and L(i ) is measured in decibels.
Find the decibel measure of the sound.
32. Ticking watch (intensity is 100 times i
0
).
33. Soft music (intensity is 10,000 times i
0
).
34. Loud conversation (intensity is 4 million times i
0
).
35. Victoria Falls in Africa (intensity is 10 billion times i
0
).
36. How much louder is the sound in Exercise 33 than the sound
in Exercise 32?
37. The perceived loudness L of a sound of intensity I is given
by L k
ln I, where k is a certain constant. By how much
must the intensity be increased to double the loudness?
(That is, what must be done to I to produce 2L?)
THINKERS
38. Compute each of the following pairs of numbers.
(a) log 18 and
l
l
n
n
1
1
8
0
(b) log 456 and
l
l
n
n
4
1
5
0
6
(c) log 8950 and
ln
ln
89
1
5
0
0
(d) What do these results suggest?
39. Prove that for any positive number c, log c
ln
ln
1
c
0
. [Hint:
We know that 10
log c
c (why?). Take natural logarithms
on both sides and use a logarithm law to simplify and solve
for log c.]
40. Find each of the following logarithms.
(a) log 8.753 (b) log 87.53 (c) log 875.3
(d) log 8753 (e) log 87,530
(f ) How are the numbers 8.753, 87.53, . . . , 87,530 related
to one another? How are their logarithms related? State
a general conclusion that this evidence suggests.
41. Prove that for every positive number c, log c can be
written in the form k log b, where k is an integer and
1 b 10. [Hint: Write c in scientific notation and use
logarithm laws to express log c in the required form.]
42. A scientist is measuring the spread of a rumor over time. She
notices a nice pattern when she graphs the natural logarithm
of the number of people who know the rumor after t days:
(a) Find a good model for the number of people who know
the rumor at a given time t, where 0 t 30
(b) A friend of the scientist wonders why she didn’t just
graph the number of people instead of the logarithm of
the number of people. What was the advantage of using
the logarithm in the graph?
10502015 3025
Days
People
0
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
x
y
392 CHAPTER 5 Exponential and Logarithmic Functions
43. Wayland and Christy have been tracking the number of
cases of flu in their city:
Wayland thinks this is exponential growth. Christy doesn’t
think so. After playing around with the data, they plot the
points and still disagree.
(a) Plot the points. Do you agree with Wayland or with
Christy?
(b) They create a new plot, this time using the natural log-
arithms of the number of cases. So they plot the points
(0, ln(10)), (2, ln(13)), etc. As soon as they see this new
plot, they agree! Construct this new plot.
(c) Who was right, Wayland or Christy? Why?
Weeks since January 1 0123456
Number of cases 10 13 16 20 24 31 38
5.4.A SPECIAL TOPICS Logarithmic Functions to Other Bases*
■ Learn the definition and properties of logarithms to any base b.
■ Use the Change of Base formula to evaluate logarithms to base b.
The same procedure used in Sections 5.3–5.4 can be carried out with any positive
number b in place of 10 and e.
Throughout this section, b is a fixed positive
number with b a 1.
†
The exponential function f (x) b
x
, whose graph is shown in Figure 5–26, is
an increasing function and hence is one-to-one (as explained on page 219). There-
fore, f has an inverse function g whose graph is the reflection of the graph of f in
the line y x (see page 225), as shown in Figure 5–27.
Figure 5–26 Figure 5–27
This inverse function g is called the logarithmic function to the base b. The
value g(x) of this function at a number x is denoted log
b
x and called the loga-
rithm to the base b of the number x.
In Section 3.7, we saw that the relationship between a function f and its in-
verse function g is given by
g(v) u exactly when f (u) v.
When f (x) b
x
and g(x) log
b
x, this statement takes the following form.
x
y
y = x
1
1
g(x)
f(x)
x
y
f(x) = b
x
1
Section Objectives
*This material is not needed in the sequel and may be read before Section 5.3 if desired. Section 3.7
(Inverse Functions) is a prerequisite for this section, which replicates the discussion of Sections 5.3
and 5.4 in a more general context.
†
The discussion is also valid when 0 b 1, but in that case, the graphs have a different shape.

EXAMPLE 1
Translate:
(a) log
3
(14) 2.4022* into an equivalent exponential statement
(b) 4
2.67
40.504 into an equivalent logarithmic statement
SOLUTION
(a) Using the preceding definition, we see that log
3
(14) 2.4022 is equivalent to
3
2.4022
14.
(b) Similarly, 4
2.67
40.504 is equivalent to log
4
(40.504)) 2.67. ■
EXAMPLE 2
Compute the following logarithms
(a) log
2
16 (b) log
5
1/5 (c) log
7
1
(d) log
b
(10) where b is greater than 1
SOLUTION
(a) To find log
2
16, ask yourself, “What power of 2 equals 16?” Since 2
4
16,
we see that log
2
16 4.
(b) Similarly, log
5
(1/5) 1 because 5
1
1/5.
(c) We know that 7
0
1, so log
7
1 0.
(d) What power of b equals 10? The graph of f(x) b
x
in figure 5–26 shows
that every power of b is positive. So b
x
can never be 10 or any negative
number or zero, and hence log
b
(10) is not defined. ■
EXAMPLE 3
Logarithms to the base 10 are called common logarithms. Is it customary to write
log v instead of log
10
v. Then
log 100 2 because 10
2
100;
log .001 3 because 10
3
1
1
0
3
10
1
00
.001.
SPECIAL TOPICS 5.4.A Logarithmic Functions to Other Bases 393
Definition of
Logarithms to
Base b
Let u and v be real numbers, with v 0. Then
log
b
v u exactly when b
u
v.
In other words,
log
b
v is the exponent to which b must be raised to produce v.
*Here and below, all logarithms are rounded to four decimal places. So, strictly speaking, the equal
sign should be replaced by an “approximately equal” sign ().

Calculators have a LOG key for evaluating common logarithms. For instance,
log .4 .3979, log 45.3 1.6561, log 685 2.8357. ■
EXAMPLE 4
The most frequently used base for logarithms in modern applications is the num-
ber e ( 2.71828
). Logarithms to the base e are called natural logarithms
and use a different notation: We write ln v instead of log
e
v. Calculators also have
an LN key for evaluating natural logarithms. For example,
ln .5 0.6931, ln 65 4.1744, ln 158 5.0626. ■
You don’t need a calculator to understand the essential properties of loga-
rithms. You need only translate logarithmic statements into exponential ones (or
vice versa).
EXAMPLE 5
Assume b 1.
(a) Compute log
b
1 (b) Compute log
b
b (c) Compute log
b
b
k
SOLUTION
(a) To what power must b be raised to produce 1? The answer is that b
0
1,
therefore log
b
1 0.
(b) To what power must b be raised to produce b? We know that b
1
b; there-
fore log
b
b 1.
(c) To what power must b be raised to produce b
k
? Obviously, b
k
b
k
, therefore
log
b
b
k
k. This property holds even when k is a complicated expression.
For instance, if x and y are positive, then log
6
6
3xy
3x y
(here k
3x y
). ■
EXAMPLE 6
Compute 10
log 439
SOLUTION By definition, log 439 is the power to which 10 must be raised to
produce 439. So 10
log 439
439. Similarly, if b 1, b
log
b
v
⫽ v, for every v 0.
■
Here is a summary of the facts illustrated in Examples 2(d), 5 and 6.
394 CHAPTER 5 Exponential and Logarithmic Functions
Properties
of Logarithms
1. log
b
v is defined only when v 0.
2. log
b
1 0 and log
b
b 1.
3. log
b
(b
k
) k for every real number k.
4. b
log
b
v
v for every v 0.
LOGARITHM LAWS
The first law of exponents states that b
m
b
n
b
mn
, or in words,
The exponent of a product is the sum of the exponents of the factors.
Since logarithms are just particular kinds of exponents, this statement translates as
follows.
The logarithm of a product is the sum of the logarithms of the factors.
The second and third laws of exponents, namely, b
m
/b
n
b
mn
and (b
m
)
k
b
mk
,
can also be translated into logarithmic language.
SPECIAL TOPICS 5.4.A Logarithmic Functions to Other Bases 395
Logarithm
Laws
Let b, v, w, k be real numbers, with b, v, w positive and b 1.
Product Law: log
b
(vw) log
b
v log
b
w.
Quotient Law: log
b
w
v
log
b
v log
b
w.
Power Law: log
b
(v
k
) k(log
b
v).
Proof of the Quotient Law According to Property 4 in the box on page 394,
b
log
b
v
v and b
log
b
w
w.
Therefore, by the second law of exponents (with m log
b
v and n log
b
w), we
have
w
v
b
b
l
l
o
o
g
g
b
b
w
v
b
log
b
vlog
b
w
.
Since log
b
(v/w) is the exponent to which b must be raised to produce v/w, we
must have log
b
(v/w) log
b
v log
b
w. This proves the Quotient Law. The
Product and Power Laws are proved in a similar fashion. ■
EXAMPLE 7
Simplify and write as a single logarithm.
(a) log
3
(x 2) log
3
y log
3
(x
2
4)
(b) 3 log
5
(125x)
SOLUTION
(a) log
3
(x 2) log
3
y log
3
(x
2
4)
log
3
[(x 2)y] log
3
(x
2
4) [Product Law]
log
3
(
x
x
2
2
4
)y
[Quotient Law]
log
3
(x
(x
2
)(x
2)
y
2)
[Factor denominator]
log
3
x
y
2
[Cancel common factor]
