Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

356 CHAPTER 5 Exponential and Logarithmic Functions
28. What is the radius of the base of a cone whose surface area
is 18p square centimeters and whose height is 4 cm?
29. Find the radius of the base of a conical container whose
height is 1/3 of the radius and whose volume is 180 cubic
inches. [Note: The volume of a cone of radius r and height
h is pr
2
h/3.]
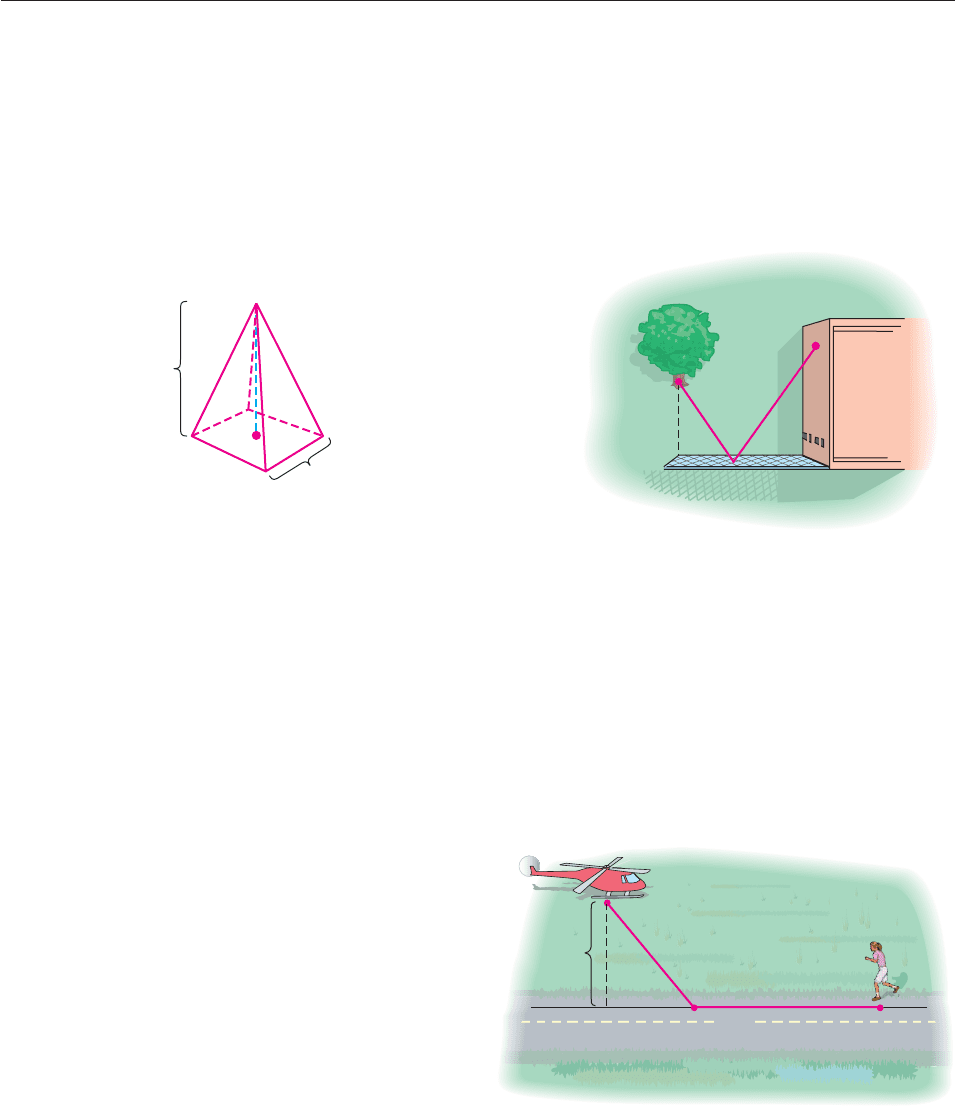
30. The surface area of the right square pyramid in the figure
is given by S b
b
2
4
h
2
. If the pyramid has height
10 feet and surface area 100 square feet, what is the length
of a side b of its base?
In Exercises 31–34, assume that all letters represent positive
numbers and solve each equation for the required letter.
31. A
1
a
b
2
2
for b
32. T 2p
m
g
for g
33. y
34. R
d
2
k
2
for d
In Exercises 35–42, solve each equation algebraically.
35. x 4x
1/2
4 0 [Hint: Let u x
1/2
.]
36. x x
1/2
12 0
37. 2x 8x
24 0
38. 3x 11x
4 0
39. x
2/3
3x
1/3
2 0 [Hint: Let u x
1/3
.]
40. x
4/3
4x
2/3
3 0
41. x
1/2
x
1/4
2 0 [Hint: Let u x
1/4
.]
42. x
1/3
x
1/6
2 0
In Exercises 43–46, solve each equation graphically.
43. x
3/5
2x
2/5
x
1/5
6 0
44. x
5/3
x
4/3
3x
2/3
x 5
45. x
3
2x
2
4x
1
5 0
46. x
2/3
3x
1/3
4
1
1 x
2
h
b
47. A rope is to be stretched at uniform height from a tree to a
35-foot-long fence, which is 20 feet from the tree, and then
to the side of a building at a point 30 feet from the fence, as
shown in the figure.
(a) If 63 feet of rope is to be used, how far from the build-
ing wall should the rope meet the fence?
(b) How far from the building wall should the rope meet
the fence if as little rope as possible is to be used?
48. Anne is standing on a straight road and wants to reach her
helicopter, which is located 2 miles down the road from her,
a mile from the road in a field (see the figure). She can run
5 miles per hour on the road and 3 miles per hour in the
field. She plans to run down the road, then cut diagonally
across the field to reach the helicopter.
(a) If she reaches the helicopter in exactly 42 minutes
(.7 hours) where did she leave the road?
(b) Where should she leave the road to reach the helicopter
as soon as possible?
49. A power plant is located on the bank of a river that is
1
2
mile wide. Wiring is to be laid across the river and then
along the shore to a substation 8 miles downstream, as
shown in the figure. It costs $12,000 per mile for underwa-
ter wiring and $8000 per mile for wiring on land. If $72,000
Anne
Helicopter
1 mile
Road
Field
30
20
Fence
Tree
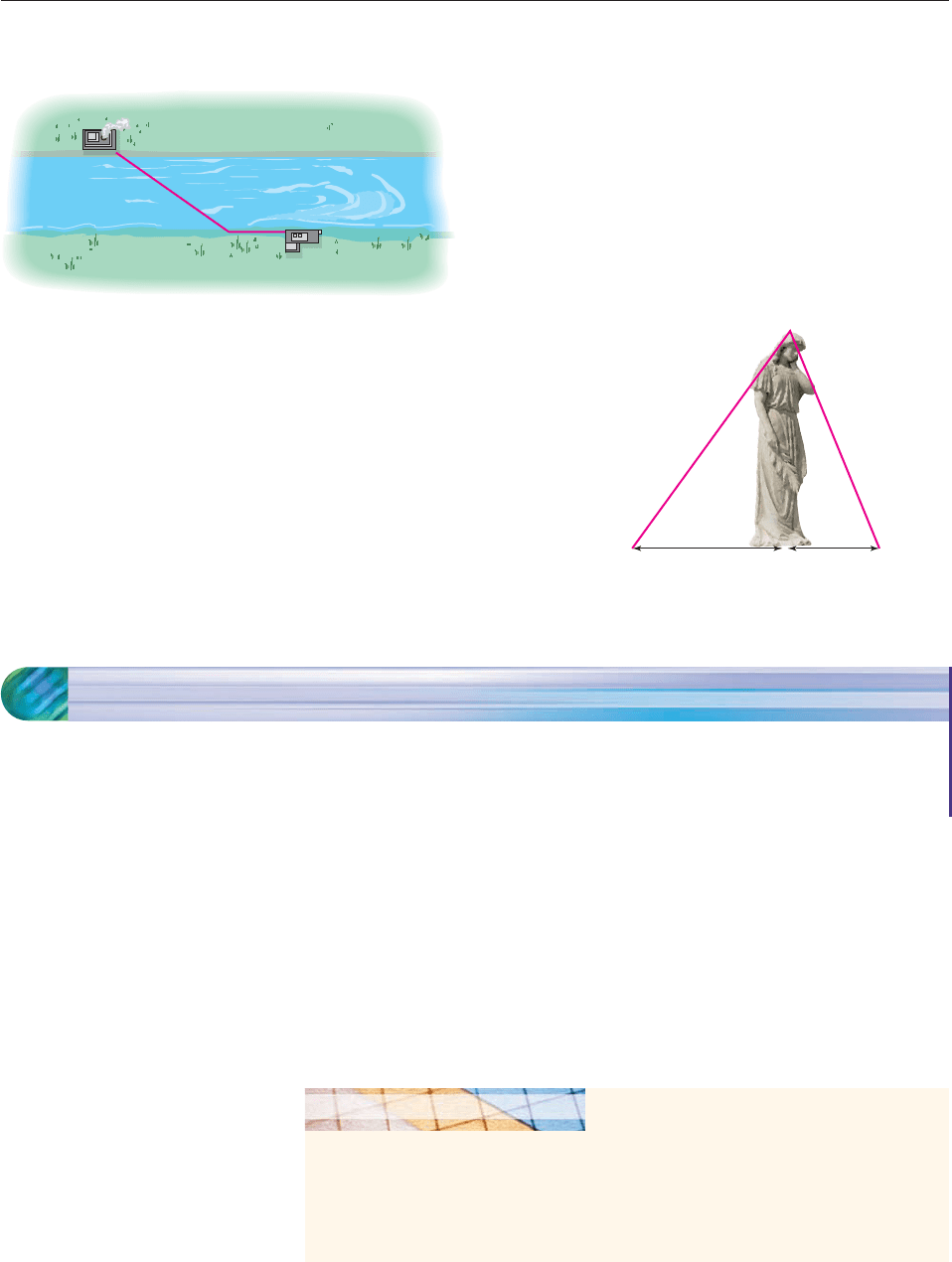
SECTION 5.2 Exponential Functions 357
is to be spent on the project, how far from the substation
should the wiring come to shore?
50. A spotlight is to be placed on a building wall to illuminate a
bench that is 32 feet from the base of the wall. The intensity
I of the light at the bench is known to be x/d
3
, where x is the
height of the spotlight above the ground and d is the dis-
tance from the bench to the spotlight.
(a) Express I as a function of x. [It may help to draw a pic-
ture.]
(b) How high should the spotlight be in order to provide
maximum illumination at the bench?
51. If an object is dropped from a height h
0
feet, it will take
1
4
h
0
seconds to hit the ground, assuming that h
0
is small
enough that air resistance is negligible.
Power plant
Substation
(a) We wish to make a movie by dropping a running cam-
corder off of a building. From how high would we have
to drop it to make a 10-second film?
(b) How long would the camera take to hit the ground if
dropped off of the Sears Tower in Chicago? (See exam-
ple 4 of Section 1.1.)
52. In an attempt to steady a tottering, old, statue, two ropes
are tied to the top, and secured firmly to the ground.
The first rope winds up three feet from the base of the
statue. The second rope winds up five feet from the base of
the statue. If 10 total feet of rope are used, how tall is the
statue?
35
5.2 Exponential Functions
■ Explore graphs of exponential functions.
■ Use exponential functions to model growth and decay.
■ Use the natural exponential function.
For each positive real number a there is a function (called the exponential func-
tion with base a) whose domain is all real numbers and whose rule is f (x) a
x
.
For example,
f (x) 10
x
, g(x) 2
x
, h(x)
1
2
x
, k(x)
3
2
x
.
The graph of f (x) a
x
is the next entry in the catalog of basic functions. To see
how its graph depends on the size of the base a, do the following Graphing
Exploration.
Section Objectives
Using viewing window with 3 x 7 and 2 y 18, graph
f (x) 1.3
x
, g(x) 2
x
, and h(x) 10
x
on the same screen. How is the steepness of the graph of f (x) a
x
related to the
size of a?
GRAPHING EXPLORATION
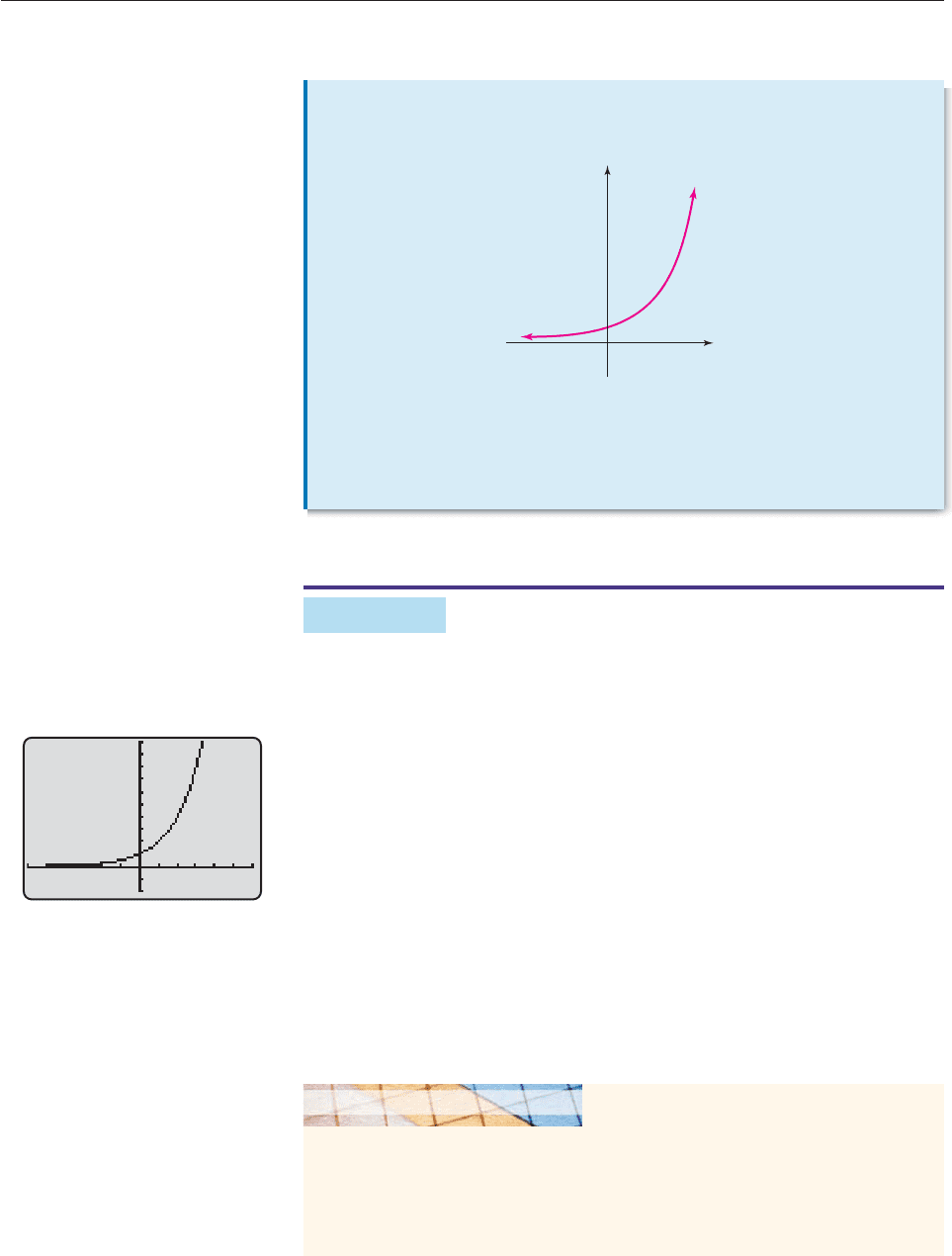
EXAMPLE 1
Graph f (x) 2
x
and estimate the height of the graph when x 50.
SOLUTION A small portion of the graph is shown in Figure 5–7. If the x-axis
were to be extended with the same scale, x 50 would be at the right edge of
the page. At that point, the height of the graph is f (50) 2
50
. Now the y-axis
scale in Figure 5–7 is approximately 12 units to the inch, which is equivalent to
760,320 units per mile, as you can readily verify. Therefore, the height of the
graph at x 50 is
76
2
0
5
,3
0
20
1,480,823,741 MILES,
which would put that part of the graph well beyond the planet Saturn! ■
When the base a is between 0 and 1, then the graph of f (x) a
x
has a differ-
ent shape.
358 CHAPTER 5 Exponential and Logarithmic Functions
The Exponential Function
f (x) a
x
(a a 1)
When a 1, the graph of f(x) a
x
has the shape shown here and the prop-
erties listed below.
The negative x-axis is a horizontal
asymptote.
The larger the base a, the more steeply
the graph rises to the right.
x
y
1
The graph is above the x-axis.
The y-intercept is 1.
f (x) is an increasing function.
The Graphing Exploration illustrates these facts:
Using viewing window with 4 x 4 and 1 y 4, graph
f (x) .2
x
, g(x) .4
x
, h(x) .6
x
, and k(x) .8
x
on the same screen. How is the steepness of the graph of f (x) a
x
related to the size
of a?
GRAPHING EXPLORATION
10
6
−6
−2
Figure 5–7

The exploration supports this conclusion.
SECTION 5.2 Exponential Functions 359
The Exponential Function
f (x) a
x
(0 b a b 1)
When 0 a 1, the graph of f (x) a
x
has the shape shown here and the
properties listed below.
The positive x-axis is a horizontal
asymptote.
The closer the base a is to 0, the more
steeply the graph falls to the right.
x
y
1
The graph is above the x-axis.
The y-intercept is 1.
f (x) is a decreasing function.
EXAMPLE 2
Without graphing, describe the graph of g(x) 3
x
.
SOLUTION Note that
g(x) 3
x
(3
1
)
x
1
3
x
.
So g(x) is an exponential function with a positive base less than 1. Its graph has
the shape shown in the preceding box: It falls quickly to the right and rises very
steeply to the left of the y-axis. ■
Exponential functions that model real-life situations generally have the form
f (x) Pa
kx
, such as
f (x) 5
2
.45x
, g(x) 3.5(10
.03x
), h(x) (6)(1.076
2x
).
Their graphs have the same basic shape as the graph of f (x) a
x
, but rise or fall
at different rates, depending on the constants P, a, and k.
EXAMPLE 3
Figure 5–8 on the next page shows the graphs of
f (x) 3
x
, g(x) 3
.15x
, h(x) 3
.35x
, k(x) 3
x
, p(x) 3
.4x
.
Note how the coefficient of x determines the steepness of the graph. When this
coefficient is positive, the graph rises, and when it is negative, the graph falls from
left to right.
GRAPHING EXPLORATION
Verify the analysis in Example 2
by graphing g(x) 3
x
in the
viewing window with 4 x 4
and 2 y 18.

Figure 5–8 Figure 5–9
Figure 5–9 shows the graphs of
p(x) 3
.4x
, q(x) 4
3
.4x
, r(x) (2)3
.4x
.
As we saw in Section 3.4, the graph of q(x) 4
3
.4x
is the graph of p(x) 3
.4x
stretched away from the x-axis by a factor of 4. The graph of r(x) (2)3
.4x
is
the graph of p(x) 3
.4x
stretched away from the x-axis by a factor of 2 and
reflected in the x-axis. ■
EXPONENTIAL GROWTH
Exponential functions are useful for modeling situations in which a quantity
increases by a fixed multiplier.
EXAMPLE 4
If you deposit $5000 in a savings account that pays 3% interest, compounded an-
nually, how much money is in the account after nine years?
SOLUTION After one year, the account balance is
5000 3% of 5000 5000 (.03)5000 5000(1 .03)
5000(1.03) $5150.
The initial balance has grown by a factor of 1.03. If you leave the $5150 in the ac-
count, then at the end of the second year, the balance is
5150 3% of 5150 5150 (.03)5150 5150(1 .03) 5150(1.03).
Once again, the amount at the beginning of the year has grown by a factor of 1.03.
The same thing happens every year. A balance of P dollars at the beginning of the
year grows to P(1.03). So the balance grows like this:
Year 1 Year 2 Year 3
5000 5000(1.03) [5000(1.03)](1.03) [5000(1.03)(1.03)](1.03)
14 4 424443 1444424443
5000(1.03)
2
5000(1.03)
3
Consequently, the balance at the end of year x is given by
f (x) 5000
1.03
x
.
The balance at the end of nine years is f (9) 5000(1.03
9
) $6523.87 (rounded
to the nearest penny). ■
10
5
−5
−10
3
−.4x
4
.
3
−.4x
(
−2
)
3
−.4x
8
5
−5
−1
3
−.4x
3
.35x
3
.15x
3
−x
3
x
360 CHAPTER 5 Exponential and Logarithmic Functions
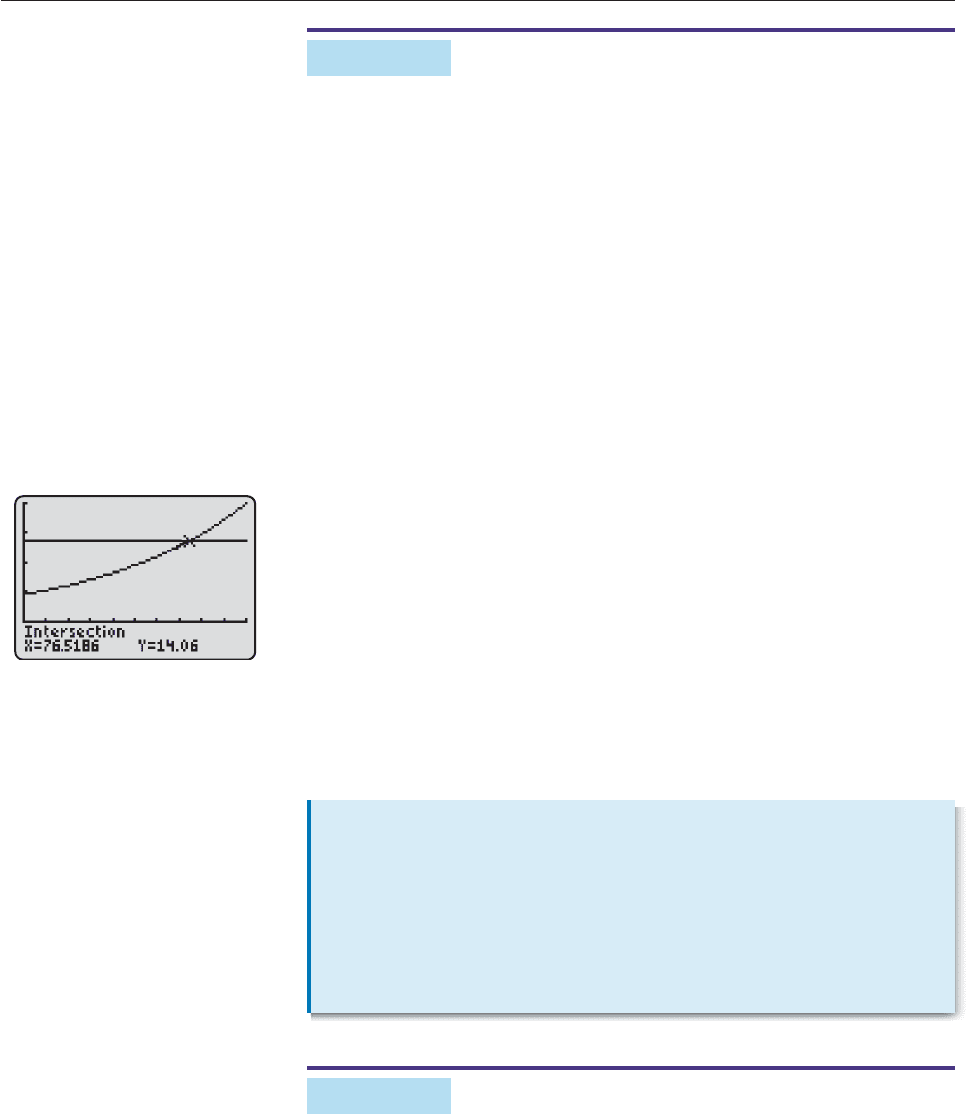
EXAMPLE 5
The world population in 1980 was about 4.5 billion people and has been increas-
ing at approximately 1.5% per year.
(a) Estimate the world population in 2010.
(b) In what year will the population be double what it is in 2010?
SOLUTION
(a) The world population in 1981 was
4.5 1.5% of 4.5 4.5 .015(4.5) 4.5(1 .015) 4.5(1.015).
Similarly, in each successive year, the population increased by a factor of
1.015, so the population (in billions) in year x is given by
g(x) 4.5(1.015
x
),
where x 0 corresponds to 1980. The year 2010 corresponds to x 30, so
the population then is g(30) 4.5(1.015
30
) 7.03 billion people.
(b) Twice the population in 2010 is 2(7.03) 14.06 billion. We must find the
number x such that g(x) 14.06; that is, we must solve the equation
4.5(1.015
x
) 14.06.
This can be done with an equation solver or by graphical means, as in Fig-
ure 5–10, which shows the intersection point of y 4.5(1.015
x
) and y
14.06. The solution is x 76.5, which corresponds to the year 2056. Thus,
according to this model, the world population will double in your lifetime.
This is what is meant by the population explosion. ■
Examples 4 and 5 illustrate exponential growth. The functions developed
there, f (x) 5000(1.03
x
) and g(x) 4.5(1.015
x
), are typical of the general case.
SECTION 5.2 Exponential Functions 361
Exponential
Growth
Exponential growth can be described by a function of the form
f (x) Pa
x
,
where f (x) is the quantity at time x, P is the initial quantity (when x 0) and
a 1 is the factor by which the quantity changes when x increases by 1.
If the quantity is growing at the rate r per time period, then a 1 r, and
f (x) Pa
x
P(1 r)
x
.
20
100
0
Figure 5–10
EXAMPLE 6
At the beginning of an experiment, a culture contains 1000 bacteria. Five hours
later, there are 7600 bacteria. Assuming that the bacteria grow exponentially, how
many will there be after 24 hours?
SOLUTION The bacterial population is given by f (x) Pa
x
, where P is the
initial population, a is the change factor, and x is the time in hours. We are given
that P 1000, so f (x) 1000a
x
. The next step is to determine a. Since there are
7600 bacteria when x 5, we have
7600 f (5) 1000a
5
,
so
1000 a
5
7600
a
5
7.6
a
5
7.6
(7.6)
.2
.
Therefore, the population function is f (x) 1000(7.6
.2
)
x
1000
(7.6)
.2x
. After
24 hours, the bacteria population will be
f (24) 1000(7.6)
.2(24)
16,900,721. ■
EXPONENTIAL DECAY
In some situations, a quantity decreases by a fixed multiplier as time goes on.
EXAMPLE 7
When tap water is filtered through a layer of charcoal and other purifying agents,
30% of the chemical impurities in the water are removed, and 70% remain. If the
water is filtered through a second purifying layer, then the amount of impurities
remaining is 70% of 70%, that is, (.7)(.7) .7
2
.49 or 49%. A third layer results
in .7
3
of the impurities remaining. Thus, the function
f(x) .7
x
gives the percentage of impurities remaining in the water after it passes through x
layers of purifying material. How many layers are needed to ensure that 95% of
the impurities are removed from the water?
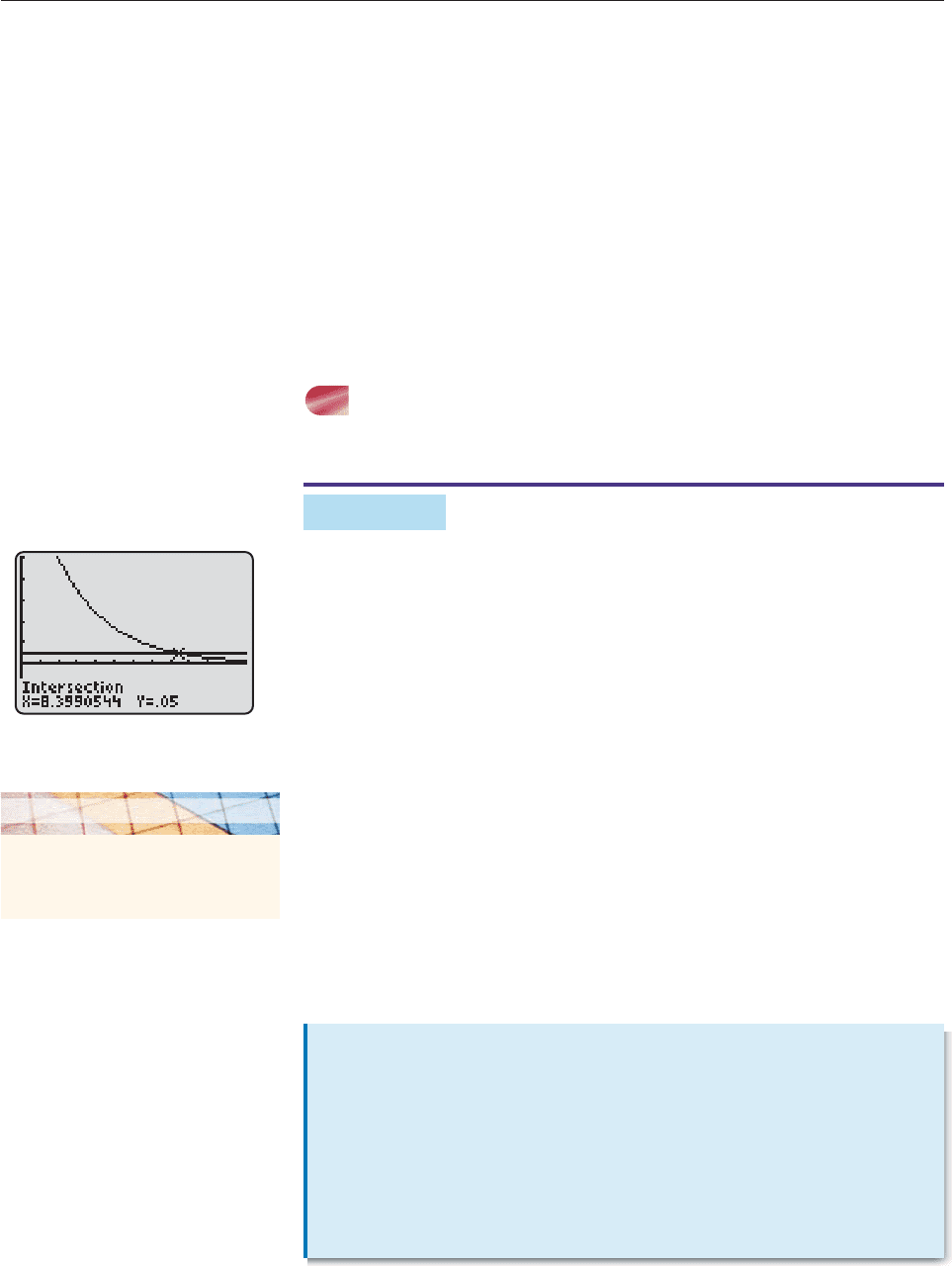
SOLUTION If 95% of the impurities are removed, then 5% will remain.
Hence, we must find x such that f (x) .05, that is, we must solve the equation
.7
x
.05. This can be done numerically or graphically. Figure 5–11 shows that the
solution is x 8.4, so 8.4 layers of material are needed. ■
Example 7 illustrates exponential decay. Note that the impurities were re-
moved at a rate of 30% .3 and that the amount of impurities remaining in the water
was changing by a factor of 1 .30 .7. The same thing is true in the general case.
362 CHAPTER 5 Exponential and Logarithmic Functions
GRAPHING EXPLORATION
Determine how many layers are
needed to ensure that 99% of the
impurities are removed.
Exponential
Decay
Exponential decay can be described by a function of the form
f (x) Pa
x
,
where f (x) is the quantity at time x, P is the initial quantity (when x 0)
and 0 a 1. Here, a is the factor by which the quantity changes when
x increases by 1.
If the quantity is decaying at the rate r per time period, then a 1 r, and
f (x) Pa
x
P(1 r)
x
.
012
−.2
.5
Figure 5–11
One of the important uses of exponential functions is to describe radioactive
decay. The half-life of a radioactive element is the time it takes a given quantity
to decay to one-half of its original mass. The half-life depends only on the sub-
stance and not on the size of the sample. Exercise 82 proves the following result.
EXAMPLE 8
Plutonium (
239
Pu) has a half-life of 24,360 years. So the amount remaining from
1 kilogram after x years is given by
M(x) 1(.5
x/24360
) (.5
1/24360
)
x
.99997
x
.
Thus, M is an exponential function whose base is very close to 1. Its graph falls
very slowly from left to right, as you can easily verify by graphing M in a window
with 0 x 2000. This means that even after an extremely long time, a substan-
tial amount of plutonium will remain. In fact, most of the original kilogram is still
there after ten thousand years because M(10,000) .75 kg. This is the reason that
nuclear waste disposal is such a serious problem. ■
THE NUMBER e AND THE NATURAL
EXPONENTIAL FUNCTION
There is an irrational number, denoted e, that arises naturally in a variety of phe-
nomena and plays a central role in the mathematical description of the physical
universe. Its decimal expansion begins
e 2.718281828459045
.
Your calculator has an e
x
key that can be used to evaluate the natural exponen-
tial function f (x) e
x
. If you key in e
1
, the calculator will display the first part of
the decimal expansion of e.
The graph of f (x) e
x
has the same shape as the graph of g(x) 2
x
in
Figure 5–7 but climbs more steeply.
EXAMPLE 9
Population Growth If the population of the United States continues to grow as
it has recently, then the approximate population of the United States (in millions)
in year t will be given by the function
P(t) 227e
.0093t
,
where 1980 corresponds to t 0.
SECTION 5.2 Exponential Functions 363
Radioactive
Decay
The mass M(x) of a radioactive element at time x is given by
M(x) c(.5
x/h
),
where c is the original mass and h is the half-life of the element.
Graph f (x) e
x
, g(x) 2
x
, and h(x) 3
x
on the same screen in a window with
5 x 5. The Technology Tip in the margin may be helpful.
GRAPHING EXPLORATION
TECHNOLOGY TIP
On most calculators, you use the e
x
key, not the x
y
or
keys to enter the
function f (x) e
x
.

(a) Estimate the population in 2015.
(b) When will the population reach half a billion?
SOLUTION
(a) The population in 2015 (that is, t 35) will be approximately
P(35) 227e
.0093(35)
314.3 million people.
(b) Half a billion is 500 million people. So we must find the value of t for which
P(t) 500, that is, we must solve the equation
227e
.0093t
500.
This can be done graphically by finding the intersection of the graph of P(t) and
the horizontal line y 500, which occurs when t 84.9 (Figure 5–12). There-
fore, the population will reach half a billion late in the year 2064. ■
OTHER EXPONENTIAL FUNCTIONS
The population growth models in earlier examples do not take into account factors
that may limit population growth in the future (wars, new diseases, etc.). Example
10 illustrates a function, called a logistic model, that is designed to model such
situations more accurately.
EXAMPLE 10
Inhibited Population Growth There is an upper limit on the fish population in
a certain lake due to the oxygen supply, available food, etc. The population of fish
in this lake at time t months is given by the function
p(t)
1
20
2
,0
4
0
e
0
t/4
(t 0).
What is the upper limit on the fish population?
SOLUTION The graph of p(t) in Figure 5–13 suggests that the horizontal line
y 20,000 is a horizontal asymptote of the graph.
In other words, the fish population never goes above 20,000. You can confirm
this algebraically by rewriting the rule of p in this form.
p(t)
1
20
2
,0
4
0
e
0
t/4
.
When t is very large, so is t/4, which means that e
t/4
is huge. Hence, by the Big-
Little Principle (page 288),
e
2
t/
4
4
is very close to 0, and p(t) is very close to
2
1
0
,00
0
0
20,000. Since e
t/4
is positive, the denominator of p(t) is slightly bigger
than 1, so p(t) is always less than 20,000. ■
When a cable, such as a power line, is suspended between towers of equal
height as in Figure 5–14, it forms a curve called a catenary, which is the graph of
a function of the form
f (x) A(e
kx
e
kx
)
20,000
1
e
2
t/
4
4
364 CHAPTER 5 Exponential and Logarithmic Functions
0
100
−200
800
Figure 5–12
050
0
25,000
Figure 5–13
for suitable constants A and k. The Gateway Arch in St. Louis (Figure 5–15) has
the shape of an inverted catenary, which was chosen because it evenly distributes
the internal structural forces.
Figure 5–15
SECTION 5.2 Exponential Functions 365
Figure 5–14
Graph each of the following functions in the window with 5 x 5 and
10 y 80.
y
1
10(e
.4x
e
.4x
), y
2
10(e
2x
e
2x
),
y
3
10(e
3x
e
3x
).
How does the coefficient of x affect the shape of the graph?
Predict the shape of the graph of y y
1
80. Confirm your answer by graphing.
GRAPHING EXPLORATION
EXERCISES 5.2
In Exercises 1–10, sketch a complete graph of the function.
1. f (x) 3
x
2. f (x) (1.001)
x
3. g(x) (5/2)
x
4. g(x) (1.001)
x
5. h(x) (1/)
x
6. h(x) (1/e)
x
7. f(x) 1 2
x
8. g(x) (1.2)
x
(.8)
x
9. h(x) 2
x
2
10. h(x) 2
x
2
In Exercises 11–16, list the transformations needed to trans-
form the graph of h(x) 2
x
into the graph of the given func-
tion. [Section 3.4 may be helpful.]
11. f(x) 2
x
5 12. g(x) (2
x
)
