Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

COMMON LOGARITHMS
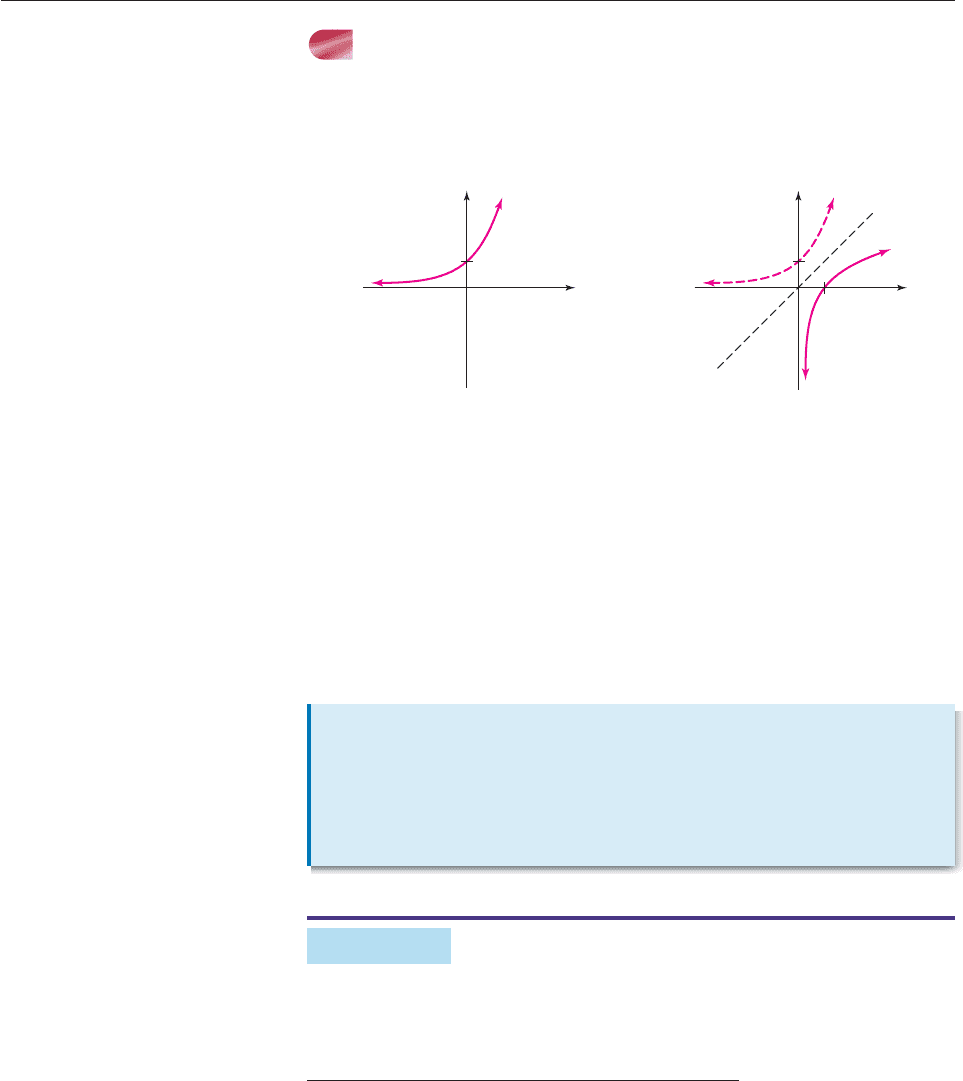
The exponential function f (x) 10
x
, whose graph is shown in Figure 5–18, is an
increasing function and hence is one-to-one (as explained on page 219). There-
fore, f has an inverse function g whose graph is the reflection of the graph of f in
the line y x (see page 225), as shown in Figure 5–19.*
Figure 5–18 Figure 5–19
This inverse function g is called the common logarithmic function. The value of
this function at the number x is denoted log x and called the common logarithm
of the number x. Every calculator has a LOG key for evaluating the function
g(x) log x. For instance,
log .01 2, log .6 .2218, and log 10000 5
†
As we saw in Section 3.7, the relationship between a function f and its inverse
function g is given by
g(v) u exactly when f (u) v.
When f (x) 10
x
and g(x) log x, this statement takes the following form.
EXAMPLE 1
Without using a calculator, find
(a) log 1000 (b) log 1 (c) log 10 (d) log
1
10
x
y
y = x
1
1
g(x)
f(x)
x
y
f(x) = 10
x
1
376 CHAPTER 5 Exponential and Logarithmic Functions
Definition of
Common Logarithms
Let u and v be real numbers, with v 0. Then
log v u exactly when 10
u
v.
In other words,
log v is the exponent to which 10 must be raised to produce v.
*Parametric equations for the graph of f (x) 10
x
can be obtained by letting
x t and y 10
t
(t any real number).
As explained on page 224, parametric equations for the graph of the inverse function g can then be
obtained by letting
x 10
t
and y t (t any real number).
This trick will allow you to display the graphs of Figure 5–19 on your calculator in parametric mode.
†
Here and below, all logarithms are rounded to four decimal places, and an equal sign is used rather
than the more correct “approximately equal.” The word “common” will be omitted except when it is
necessary to distinguish these logarithms from other types that are introduced below.

SOLUTION
(a) To find log 1000, ask yourself, “What power of 10 equals 1000?” The answer
is 3 because 10
3
1000. Therefore, log 1000 3.
(b) To what power must 10 be raised to produce 1? Since 10
0
1, we conclude
that log 1 0.
(c) Log 10 1/2 because 1/2 is the exponent to which 10 must be raised to
produce 10, that is 10
1/2
10.
(d) Log
1
10
1/2 because 10
1/2
1
10
. ■
EXAMPLE 2
Translate each of the following logarithmic statements into an equivalent expo-
nential statement.
log 29 1.4624 log .47 .3279 log (k t) d.
SOLUTION Using the definition above, we have these translations.
Logarithmic Statement Equivalent Exponential Statement
log 29 1.4624 10
1.4624
29
log .47 .3279 10
.3279
.47
log (k t) d 10
d
k t ■
EXAMPLE 3
Translate each of the following exponential statements into an equivalent loga-
rithmic statement.
10
5.5
316,227.766 10
.66
4.5708819 10
rs
t
SOLUTION Translate as follows.
Exponential Statement Equivalent Logarithmic Statement
10
5.5
316,277.766 log 316,277.766 5.5
10
.66
4.5708819 log 4.5708819 .66
10
rs
t log t rs ■
EXAMPLE 4
Solve the equation log x 4.
SOLUTION log x 4 is equivalent to 10
4
x. So the solution is x 10,000.
■
NATURAL LOGARITHMS
Common logarithms are closely related to the exponential function f (x) 10
x
.
With the advent of calculus, however, it became clear that the most useful expo-
nential function in science and engineering is g(x) e
x
. Consequently, a new
type of logarithm, based on the number e instead of 10, was developed. This
SECTION 5.3 Common and Natural Logarithmic Functions 377

development is essentially a copy of what was done above, with some minor
changes in notation.
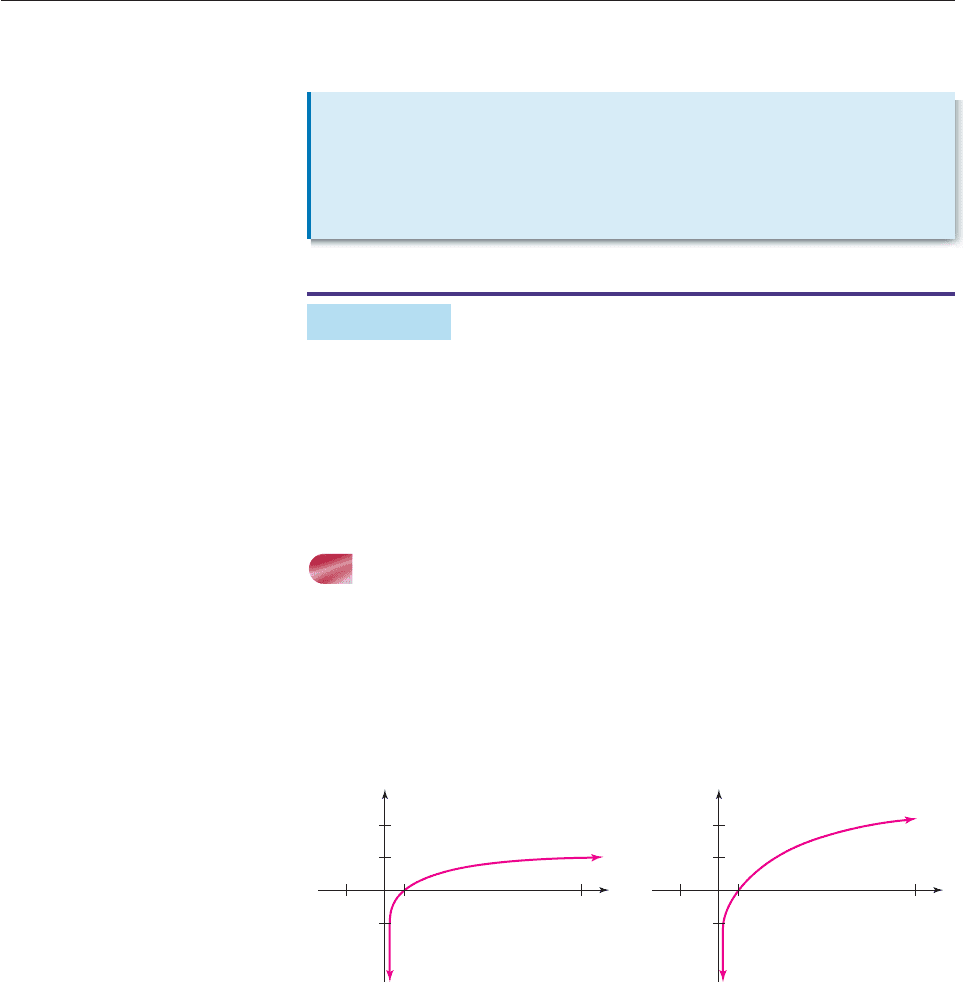
The exponential function f (x) e
x
whose graph is shown in Figure 5–20 is
increasing and hence one-to-one, so f has an inverse function g whose graph is the
reflection of the graph of f in the line y x, as shown in Figure 5–21.
Figure 5–20 Figure 5–21
This inverse function g is called the natural logarithmic function. The value g(x)
of this function at a number x is denoted ln x and called the natural logarithm of
the number x. Every calculator has an LN key for evaluating natural logarithms.
For instance,
ln .15 1.8971, ln 186 5.2257, and ln 2.718 .9999.
When the relationship of inverse functions (Section 3.7)
g(v) u exactly when f (u) v
is applied to the function f (x) e
x
and its inverse g(x) ln x, it says the
following.
EXAMPLE 5
Translate:
(a) ln 14 2.6391 into an equivalent exponential statement.
(b) e
5.0626
158 into an equivalent logarithmic statement.
SOLUTION
(a) Using the preceding definition, we see that ln 14 2.6391 is equivalent to
e
2.6391
14.
(b) Similarly, e
5.0626
158 is equivalent to ln 158 5.0626. ■
x
y
y = x
1
1
g(x)
f(x)
x
y
f(x) = e
x
1
378 CHAPTER 5 Exponential and Logarithmic Functions
Definition of
Natural Logarithms
Let u and v be real numbers, with v 0. Then
ln v u exactly when e
u
v.
In other words,
ln v is the exponent to which e must be raised to produce v.

SECTION 5.3 Common and Natural Logarithmic Functions 379
PROPERTIES OF LOGARITHMS
Since common and natural logarithms have almost identical definitions (just re-
place 10 by e), it is not surprising that they share the same essential properties.
You don’t need a calculator to understand these properties. You need only use the
definition of logarithms or translate logarithmic statements into equivalent expo-
nential ones (or vice versa).
EXAMPLE 6
What is ln (10)?
Translation: To what power must e be raised to produce 10?
Answer: The graph of f (x) e
x
in Figure 5–20 shows that every power of e is
positive. So e
x
can never be 10 or any negative number or zero, and hence,
ln (10) is not defined. Similarly, log(10) is not defined because every power
of 10 is positive. Therefore,
ln v and log v are defined only when v a 0. ■
EXAMPLE 7
What is ln 1?
Translation: To what power must e be raised to produce 1?
Answer: We know that e
0
1, which means that ln 1 0. Combining this fact
with Example 1(b), we have
ln 1 0 and log 1 0. ■
EXAMPLE 8
What is ln e
9
?
Translation: To what power must e be raised to produce e
9
?
Answer: Obviously, the answer is 9. So ln e
9
9 and in general
ln e
k
k for every real number k.
Similarly,
log 10
k
k for every real number k
because k is the exponent to which 10 must be raised to produce 10
k
. In particu-
lar, when k 1, we have
ln e 1 and log 10 1. ■

EXAMPLE 9
Find 10
log 678
and e
ln 678
.
SOLUTION By definition, log 678 is the exponent to which 10 must be raised
to produce 678. So if you raise 10 to this exponent, the answer will be 678, that is,
10
log 678
678.* Similarly, ln 678 is the exponent to which e must be raised to
produce 678, so that e
ln 678
678. The same argument works with any positive
number v in place of 678:
e
ln v
v and 10
log v
v for every v a 0. ■
The facts presented in the preceding examples may be summarized as follows.
EXAMPLE 10
Applying Property 3 with k 2x
2
7x 9 shows that
ln e
2x
2
7x9
2x
2
7x 9. ■
EXAMPLE 11
Solve the equation ln(x 1) 2.
SOLUTION Since ln(x 1) 2, we have
e
ln(x1)
e
2
.
Applying Property 4 with v x 1 shows that
x 1 e
ln(x1)
e
2
x e
2
1 6.3891. ■
Property 4 has another interesting consequence. If a is any positive num-
ber, then e
ln a
a. Hence, the rule of the exponential function f (x) a
x
can be
written as
f(x) a
x
(e
ln a
)
x
e
(ln a)x
.
380 CHAPTER 5 Exponential and Logarithmic Functions
Properties of
Logarithms
Natural Logarithms Common Logarithms
1. ln v is defined only log v is defined only
when v 0; when v 0.
2. ln 1 0 and ln e 1; log 1 0 and log 10 1.
3. ln e
k
k for every real log 10
k
k for every real
number k; number k.
4. e
ln v
v for every v 0; 10
log v
v for every v 0.
*This is equivalent, in a sense, to answering the question “Who is the author whose name is Stephen
King?” The answer is described in the question!
For example, f (x) 2
x
e
(ln 2)x
e
.6931x
. Thus, we have this useful result.
EXAMPLE 12
Write f(x) 3 5
x
in the form f(x) Pe
kx
.
SOLUTION 3 5
x
3 (e
ln5
)
x
3e
ln5 x
3e
1.6094x
■
GRAPHS OF LOGARITHMIC FUNCTIONS
Figure 5–22 shows the graphs of two more entries in the catalog of basic func-
tions, f (x) log x and g(x) ln x. Both are increasing functions with these four
properties:
Domain: all positive real numbers x-intercept: 1
Range: all real numbers Vertical Asymptote: y-axis
Figure 5–22
Calculators and computers do not accurately show that the y-axis is a vertical
asymptote of these graphs. By evaluating the functions at very small numbers
(such as x 1/10
500
), you can see that the graphs go lower and lower as x gets
closer to 0. On a calculator, however, the graph will appear to end abruptly near
the y-axis (try it!).
Some viewing windows may give the impression that logarithmic graphs
(such as those in Figures 5–20 and 5–21) have horizontal asymptotes. Don’t be
fooled! These graphs have no horizontal asymptotes—the y-values get arbitrarily
large.
x
y
f(x) = log x
1
1
−1
2
10−2
x
y
g(x) = ln x
1
1
−1
2
10−2
SECTION 5.3 Common and Natural Logarithmic Functions 381
Exponential
Functions
Every exponential growth or decay function can be written in the form
f (x) Pe
kx
,
where f (x) is the amount at time x, P is the initial quantity, and k is positive
for growth and negative for decay.
EXAMPLE 13
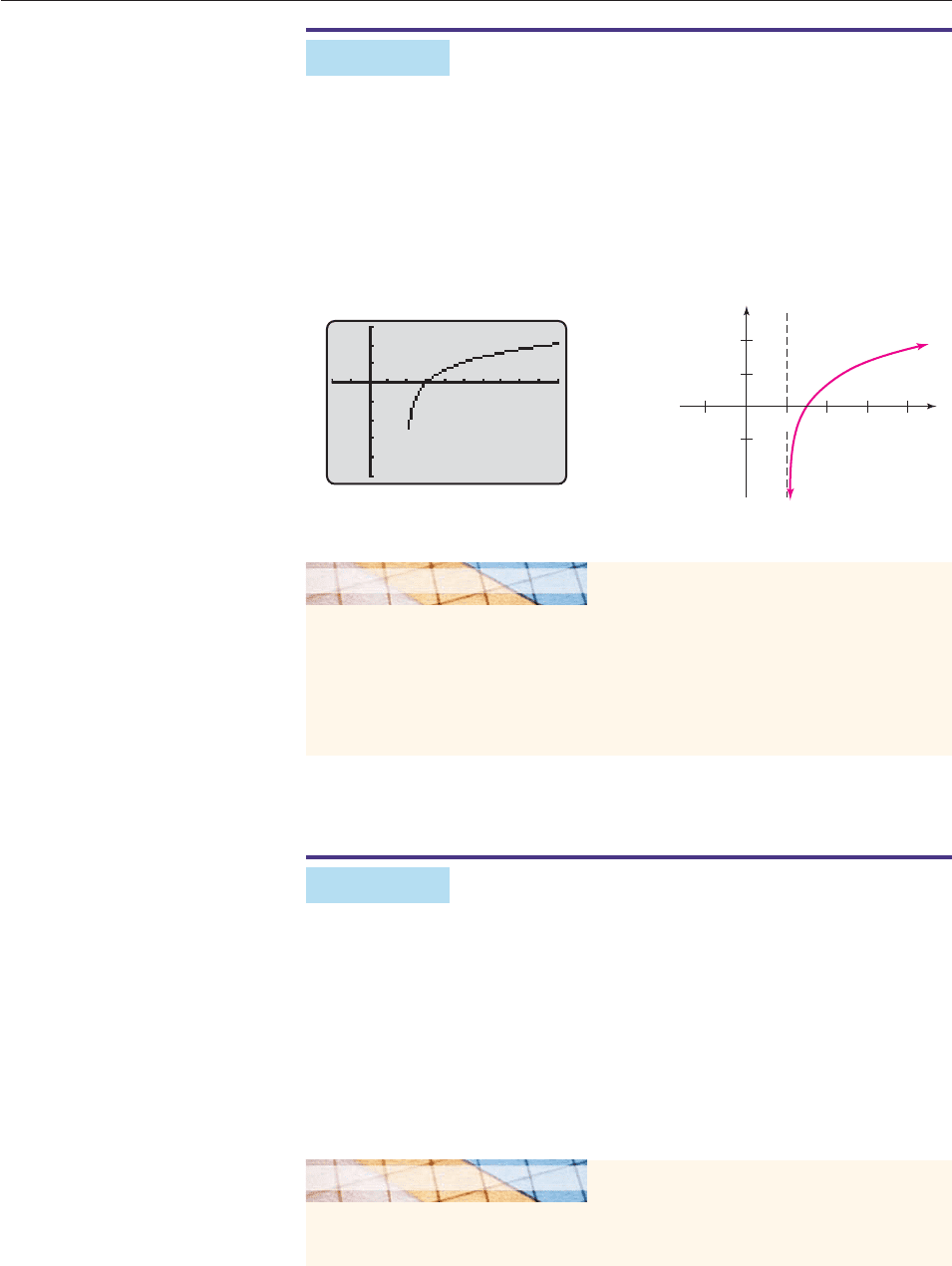
Sketch the graph of f (x) ln (x 2).
SOLUTION Using a calculator to graph f (x) ln (x 2), we obtain Figure 5–23,
in which the graph appears to end abruptly near x 2. Fortunately, however, we have
read Section 3.4, so we know that this is not how the graph looks. From Section 3.4,
we know that the graph of f (x) ln (x 2) is the graph of g(x) ln x shifted hori-
zontally 2 units to the right, as shown in Figure 5–24. In particular, the graph of f has
a vertical asymptote at x 2 and drops sharply downward there. ■
Figure 5–23 Figure 5–24
x
y
1
2
−1
2
4 6 8−2
3
−5
10
−2
382 CHAPTER 5 Exponential and Logarithmic Functions
Graph y
1
ln (x 2) and y
2
5 in the same viewing window and verify that the
graphs do not appear to intersect, as they should. Nevertheless, try to solve the equa-
tion ln (x 2) 5 by finding the intersection point of y
1
and y
2
. Some calculators
will find the intersection point even through it does not show on the screen. Others
produce an error message, in which case the SOLVER feature should be used
instead of a graphical solution.
GRAPHING EXPLORATION
Although logarithms are only defined for positive numbers, many logarith-
mic functions include negative numbers in their domains.
EXAMPLE 14
Find the domain of each of the following functions.
(a) f (x) ln (x 4) (b) g(x) log x
2
SOLUTION
(a) f (x) ln (x 4) is defined only when x 4 0, that is, when x 4. So
the domain of f consists of all real numbers greater than 4.
(b) Since x
2
0 for all nonzero x, the domain of g(x) log x
2
consists of all real
numbers except 0. ■
Verify the conclusions of Example 14 by graphing each of the functions. What is the
vertical asymptote of each graph?
GRAPHING EXPLORATION

SECTION 5.3 Common and Natural Logarithmic Functions 383
EXERCISES 5.3
Unless stated otherwise, all letters represent positive
numbers.
In Exercises 1–4, find the logarithm, without using a
calculator.
1. log 10,000 2. log .001
3. log
10
1
0
0
0
4. log
3
.01
In Exercises 5–14, translate the given logarithmic statement
into an equivalent exponential statement.
5. log 1000 3 6. log .001 3
7. log 750 2.88 8. log (.8) .097
9. ln 3 1.0986 10. log (log(x)) 1
11. ln .01 4.6052 12. ln s r
13. ln (x
2
2y) z w 14. log (a c) d
In Exercises 15–24, translate the given exponential statement
into an equivalent logarithmic statement.
15. 10
2
.01 16. 10
3
1000
17. 10
.4771
3 18. 10
3k
6r
19. e
3.25
25.79 20. e
3.14
23.1039
21. e
12/7
5.5527 22. e
k
t
23. e
2/r
w 24. e
e
15.1543
In Exercises 25–36, evaluate the given expression without
using a calculator.
25. log 10
43
26. log 10
3
r
2
s
2
27. ln e
15
28. e
ln
29. ln e
30. ln
5
e
31. e
ln 931
32. log (log(10,000,000,000))
33. ln e
xy
34. ln e
x
2
2y
35. e
ln x
2
36. e
ln(ln2)
In Exercises 37–40, write the rule of the function in the form
f(x) Pe
kx
. (See the discussion and box after Example 11.)
37. f (x) 4(25
x
) 38. g(x) 3.9(1.03
x
)
39. g(x) 16(30.5
x
) 40. f (x) 2.2(.75
x
)
In Exercises 41–42, write the rule of the function in the form
f(x) a
x
. (See the discussion and box after Example 11.)
41. g(x) e
3x
42. f(x) e
1.6094x
In Exercises 43–46, find the domain of the given function (that
is, the largest set of real numbers for which the rule produces
well-defined real numbers).
43. f (x) ln (x 1) 44. g(x) ln (x 2)
45. h(x) log (x) 46. k(x) log (ln (2) x)
47. (a) Graph y x and y e
ln x
in separate viewing windows
[or use a split-screen if your calculator has that feature].
For what values of x are the graphs identical?
(b) Use the properties of logarithms to explain your answer
in part (a).
48. (a) Graph y x and y ln (e
x
) in separate viewing win-
dows [or a split-screen if your calculator has that fea-
ture]. For what values of x are the graphs identical?
(b) Use the properties of logarithms to explain your answer
in part (a).
49. Do the graphs of f(x) log x
2
and g(x) 2 log x appear to
be the same? How do they differ?
50. Do the graphs of h(x) log x
3
and k(x) 3 log x appear to
be the same?
In Exercises 51–56, list the transformations that will change
the graph of g(x) ln x into the graph of the given function.
[Section 3.4 may be helpful.]
51. f (x) 2
ln x 52. f (x) ln x 7
53. h(x) ln (x 4) 54. k(x) ln (x 2)
55. h(x) ln (x 3) 4 56. k(x) ln (x 2) 2
In Exercises 57–60, sketch the graph of the function.
57. f (x) log (x 3) 58. g(x) 2 ln x 3
59. h(x) 2 log x 60. f (x) ln (x) 3
In Exercises 61–68, find a viewing window (or windows) that
shows a complete graph of the function.
61. f (x)
ln
x
x
62. g(x)
ln
x
x
63. h(x)
ln
x
x
2
64. k(x) e
2/ln x
65. f (x) 10 log x x 66. f (x)
lo
x
g x
67. l(x) e
e
x
68. r(x) ln(e
x
)
In Exercises 69–72, find the average rate of change of the
function.
69. f (x) ln (x 2), as x goes from 3 to 5.
70. g(x) x ln x, as x goes from .5 to 1.

384 CHAPTER 5 Exponential and Logarithmic Functions
71. g(x) log (x
2
x 1), as x goes from 5 to 3.
72. f (x) x log x, as x goes from 1 to 4.
73. (a) What is the average change of f(t) ln t, as t goes from
2 to 2 h?
(b) What is the average change of f (t) ln t, as t goes
from 2 to 2 h when h is .01? When h is .001? .0001?
.00001?
(c) What is the average change of f (t) ln t, as t goes
from 4 to 4 h when h is .01? When h is .001? .0001?
.00001?
(d) Approximate the average change of f (t) ln t, as t goes
from 5 to 5 h for very small values of h.
(e) Work some more examples like those above. What is
the average rate of change of f(t) ln t, as t goes from
x to x h for very small values of h?
74. (a) Find the average rate of change of f (x) ln x
2
, as x
goes from .5 to 2.
(b) Find the average rate of change of g(x) ln (x 3)
2
, as
x goes from 3.5 to 5.
(c) What is the relationship between your answers in parts
(a) and (b) and why is this so?
75. Show that g(x) ln
1
x
x
is the inverse function of
f (x)
1
1
e
x
. (See Section 3.7.)
76. The doubling function D(x)
ln (
l
1
n
2
x)
gives the years re-
quired to double your money when it is invested at interest
rate x (expressed as a decimal), compounded annually.
(a) Find the time it takes to double your money at each of
these interest rates: 4%, 6%, 8%, 12%, 18%, 24%,
36%.
(b) Round the answers in part (a) to the nearest year and
compare them with these numbers: 72/4, 72/6, 72/8,
72/12, 72/18, 72/24, 72/36. Use this evidence to
state a rule of thumb for determining approximate dou-
bling time, without using the function D. This rule of
thumb, which has long been used by bankers, is called
the rule of 72.
77. Suppose f (x) A ln x B, where A and B are constants. If
f (1) 10 and f (e) 1, what are A and B?
78. If f (x) A ln x B and f (e) 5 and f (e
2
) 8, what are
A and B?
79. The height h above sea level (in meters) is related to air tem-
perature t (in degrees Celsius), the atmospheric pressure p
(in centimeters of mercury at height h), and the atmospheric
pressure c at sea level by
h (30t 8000) ln (c/p).
If the pressure at the top of Mount Rainier is 44 centime-
ters on a day when sea level pressure is 75.126 centime-
ters and the temperature is 7°C, what is the height of
Mount Rainier?
80. Mount Everest is 8850 meters high. What is the atmospheric
pressure at the top of the mountain on a day when the tem-
perature is 25°C and the atmospheric pressure at sea level
is 75 centimeters? [See Exercise 79.]
81. Beef consumption in the United States (in billions of
pounds) in year x can be approximated by the function
f (x) 154.41 39.38 ln x (x 90).
where x 90 corresponds to 1990.*
(a) How much beef was consumed in 1999 and in 2002?
(b) According to this model when will beef consumption
reach 35 billion pounds per year?
82. Students in a precalculus class were given a final exam.
Each month thereafter, they took an equivalent exam. The
class average on the exam taken after t months is given by
F(t) 82 8
ln (t 1).
(a) What was the class average after six months?
(b) After a year?
(c) When did the class average drop below 55?
83. One person with a flu virus visited the campus. The
number T of days it took for the virus to infect x people
was given by:
T .93 ln
70
6
0
9
0
99
x
x
.
(a) How many days did it take for 6000 people to become
infected?
(b) After two weeks, how many people were infected?
84. The population of St. Petersburg, Florida (in thousands) can
be approximated by the function
g(x) 127.9 81.91 ln x (x 70),
where x 70 corresponds to 1970.
(a) Estimate the population in 1995 and 2003.
(b) If this model remains accurate, when will the popula-
tion be 260,000?
85. A bicycle store finds that the number N of bikes sold is
related to the number d of dollars spent on advertising by
N 51 100
ln (d/100 2).
(a) How many bikes will be sold if nothing is spent on
advertising? If $1000 is spent? If $10,000 is spent?
(b) If the average profit is $25 per bike, is it worthwhile to
spend $1000 on advertising? What about $10,000?
(c) What are the answers in part (b) if the average profit per
bike is $35?
86. Approximating Logarithmic Functions by Polynomials.
For each positive integer n, let f
n
be the polynomial function
whose rule is
f
n
(x) x
x
2
2
x
3
3
x
4
4
x
5
5
x
n
n
*Based on data from the U.S. Department of Agriculture.

where the sign of the last term is if n is odd and if n is
even. In the viewing window with 1 x 1 and
4 y 1, graph g(x) ln (1 x) and f
4
(x) on the same
screen. For what values of x does f
4
appear to be a good
approximation of g?
87. Using the viewing window in Exercise 86, find a value of n
for which the graph of the function f
n
(as defined in Exercise
86) appears to coincide with the graph of g(x) ln (1 x).
Use the trace feature to move from graph to graph to see
how good this approximation actually is.
88. Aharmonic sum is a sum of this form:
1
1
2
1
3
1
4
1
k
.
(a) Compute 1
1
2
1
3
1
4
, 1
1
2
1
3
1
4
1
5
, and
1
1
2
1
3
1
4
1
5
1
6
(b) How many terms do you need in a harmonic sum for it
to exceed three?
(c) It turns out to be hard to determine how many terms
you would need for the sum to exceed 10. It will take
thousands of terms, more than you would want to plug
into a calculator. Using calculus, we can derive this
lower-bound formula:
n
i1
1
i
ln n. It means that the
harmonic sum with n terms is always greater than ln n.
Use this formula to find a value of n such that the har-
monic sum with n terms is greater than ten.
(d) Calculus also gives us an upper-bound formula:
n
i1
1
i
ln n 1. Estimate the harmonic sum with
100,000 terms. How close is your estimate to the real
number?
89. The ancient Sumerians started using a place-value system
around 3000 BC. Assume that in 3000 BC you started adding
1
1
2
1
3
1
4
. . .
at the rate of ten additions per second.
(a) What would the value be today? Make your best guess.
(b) Use the upper-bound and lower-bound formulas given
in Exercise 88 to estimate what the value would be
today. Was your guess close?
(c) In what year are you guaranteed to be above 28.187?
SECTION 5.4 Properties of Logarithms 385
5.4 Properties of Logarithms
■ Use the Product, Quotient, and Power Laws for logarithms to
simplify logarithmic expressions.
■ Use logarithms to solve applied problems.
Logarithms have several important properties beyond those presented in Sec-
tion 5.3. These properties, which we shall call logarithm laws, arise from the fact
that logarithms are exponents. Essentially, they are properties of exponents trans-
lated into logarithmic language.
The first law of exponents says that b
m
b
n
b
mn
, or in words,
The exponent of a product is the sum of the exponents of the factors.
Since logarithms are just particular kinds of exponents, this statement translates as
follows.
The logarithm of a product is the sum of the logarithms of the factors.
Here is the same statement in symbolic language.
Before proving the Product Law, we illustrate it in the case when v 10
2
and
w 10
3
.
Section Objectives
Product Law
for Logarithms
For all v, w 0,
ln(vw) ln v ln w
and
log(vw) log v log w.
