Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


EXAMPLE 13
The number of pounds of fish (in billions) used for human consumption in the
United States in year x is approximated by the function
f (x) 10.57 1.75 ln x,
where x 5 corresponds to 1995.*
(a) How many pounds of fish were used in 2004?
(b) When will fish consumption reach 16 billion pounds?
SOLUTION
(a) Since 2004 corresponds to x 14, we evaluate f (x) at 14.
f (14) 10.57 1.75 ln 14 15.19 billion pounds.
(b) Fish consumption is 16 billion pounds when f (x) 16, so we must solve the
equation
10.57 1.75 ln x 16
Subtract 10.57 from both sides: 1.75 ln x 5.43
Divide both sides by 1.75: ln x
5
1
.
.
4
7
3
5
Exponentiate both sides: e
ln x
e
5.43/1.75
Use the basic property of logarithms (
*
): x 22.26.
Since x 22 corresponds to 2012, fish consumption will reach 16 billion
pounds in 2012. ■
406 CHAPTER 5 Exponential and Logarithmic Functions
*Based on data from the U.S. National Oceanic and Atmospheric Administration and the National
Marine Fisheries Service.
EXERCISES 5.5
In Exercises 1–8, solve the equation without using logarithms.
1. 3
x
81 2. 5
x
2 23 3. 3
x1
9
5x
4. 3
7x
9
2x5
5. 3
5x
9
x
2
27
6. 7
x
2
3x
1/49 7. 9
x
2
3
5x2
8. 5
2x
2
3x
25
6x
In Exercises 9–22, solve the equation. First express your
answer in terms of natural logarithms (for instance,
x (2 ln 5)/(ln 3)). Then use a calculator to find an approx-
imation for the answer.
9. 3
x
5 10. 2
x
9 11. 2
x
3
x1
12. 9
x1
8
x3
13. 3
12x
5
x5
14. 2
13x
7
x3
15. 2
13x
3
x1
16. 5
x3
2
x
17. e
2x
5
18. e
9x
3 19. 6e
1.4x
21
20. 27e
x/4
67.5 21. 2.1e
(x/2)ln 3
5
22. 2.7e
(x/3)ln 7
21
In Exercises 23–29, solve the equation for x by first making an
appropriate substitution, as in the Hint for Exercise 23.
23. 9
x
4
3
x
3 0[Hint: Let u 3
x
and note that
9
x
(3
2
)
x
3
2x
(3
x
)
2
. Hence, the equation becomes
u
2
4u 3 0. Solve this equation for u. In each solution,
replace u by 3
x
and solve for x.]
24. 25
x
8
5
x
12
25. e
2x
5e
x
6 0[Hint: Let u e
x
.]

26. 3e
2x
16e
x
5 0 27. 6e
2x
16e
x
6
28. 6e
2x
7e
x
10 29. 4
x
6
4
x
5
In Exercises 30–32, solve the equation for x.
30.
e
e
x
x
e
e
x
x
t 31.
e
x
2
e
x
t
32.
e
e
x
x
e
e
x
x
t
33. (a) Prove that if ln u ln v, then u v. [Hint: Property (
*
)
on page 404.]
(b) Is it always the case that if u v then ln u ln v? Why
or why not?
34. (a) Solve 7
x
3, using natural logarithms. Leave your
answer in logarithmic form; don’t approximate with a
calculator.
(b) Solve 7
x
3, using common (base 10) logarithms.
Leave your answer in logarithmic form.
(c) Use the change of base formula in Special Topics 5.4.A
to show that your answers in parts (a) and (b) are the
same.
In Exercises 35–44, solve the equation as in Example 8.
35. ln (3x 5) ln 11 ln 2
36. log (3x 8) log (2x 1) log 3
37. log (3x 1) log 2 log 4 log (x 2)
38. ln (2x 1) ln 2 ln (3x 6) ln 6
39. 2 ln x ln 36
40. 2 log x 3 log 9
41. ln x ln (x 1) ln 3 ln 4
42. ln (5x 2) ln x ln 3
43. ln x ln 3 ln (x 5)
44. ln (3x 4) ln x ln e
In Exercises 45–52, solve the equation.
45. ln (x 9) ln x 1
46. ln (3x 5) 1 ln (2x 3)
47. log x log (x 3) 1
48. log (x 4) log (x 1) 1
49. log
x
2
1
2
50. log
5
x
2
1
5x
2/5
51. ln (x
2
1) ln (x 1) 1 ln (x 1)
52.
l
l
n
n
(
(
2
3
x
x
1
1
)
)
2
Exercises 53–62 deal with radioactive decay and the function
M(x) c(.5
x/h
); see Examples 4 and 5.
53. A sample of 300 grams of uranium decays to 200 grams in
.26 billion years. Find the half-life of uranium.
SECTION 5.5 Algebraic Solutions of Exponential and Logarithmic Equations 407
54. It takes 1000 years for a sample of 300 mg of radium-226 to
decay to 195 mg. Find the half-life of radium-226.
55. A 3-gram sample of an isotope of sodium decays to 1 gram
in 23.7 days. Find the half-life of the isotope of sodium.
56. The half-life of cobalt-60 is 5.3 years. How long will it take
for 100 grams to decay to 33 grams?
57. After six days a sample of radon-222 decayed to 33.6% of
its original mass. Find the half-life of radon-222. [Hint:
When x 6, then M(x) .336P.]
58. Krypton-85 loses 6.44% of its mass each year. What is its
half-life?
59. How old is a piece of ivory that has lost 36% of its
carbon-14?
60. How old is a mummy that has lost 62% of its carbon-14?
61. A Native American mummy was found recently. If it has
lost 26.4% of its carbon-14, approximately how long ago
did the Native American die?
62. How old is a wooden statue that has only one-third of its
original carbon-14?
Exercises 63–68 deal with the compound interest formula
A P(1 r)
t
, which was discussed in Special Topics 5.2.A.
63. At what annual rate of interest should $1000 be invested so
that it will double in 10 years if interest is compounded
quarterly?
64. How long does it take $500 to triple if it is invested at 6%
compounded: (a) annually, (b) quarterly, (c) daily?
65. (a) How long will it take to triple your money if you
invest $500 at a rate of 5% per year compounded
annually?
(b) How long will it take at 5% compounded quarterly?
66. At what rate of interest (compounded annually) should you
invest $500 if you want to have $1500 in 12 years?
67. How much money should be invested at 5% interest, com-
pounded quarterly, so that 9 years later the investment will
be worth $5000? This amount is called the present value of
$5000 at 5% interest.
68. Find a formula that gives the time needed for an investment
of P dollars to double, if the interest rate is r% compounded
annually. [Hint: Solve the compound interest formula for t,
when A 2P.]
Exercises 69–76 deal with functions of the form f (x) Pe
kx
,
where k is the continuous exponential growth rate (see
Example 6).
69. The present concentration of carbon dioxide in the atmo-
sphere is 364 parts per million (ppm) and is increasing
exponentially at a continuous yearly rate of .4% (that is,
k .004). How many years will it take for the concentration
to reach 500 ppm?

70. The amount P of ozone in the atmosphere is currently de-
caying exponentially each year at a continuous rate of
1
4
%
(that is, k .0025). How long will it take for half the
ozone to disappear (that is, when will the amount be P/2)?
[Your answer is the half-life of ozone.]
71. The population of Brazil increased from 151 million in
1990 to 180 million in 2002.*
(a) At what continuous rate was the population growing
during this period?
(b) Assuming that Brazil’s population continues to increase
at this rate, when will it reach 250 million?
72. Between 1996 and 2004, the number of United States sub-
scribers to cell-phone plans has grown nearly exponentially.
In 1996 there were 44,043,000 subscribers and in 2004
there were 182,140,000
†
.
(a) What is the continuous growth rate of the number of
cell-phone subscribers?
(b) In what year were there 60,000,000 cell-phone
subscribers?
(c) Assuming that this rate continuous, in what year will
there be 350,000,000 subscribers?
(d) In 2007 the United States population was approxi-
mately 300 million. Is your answer to part (c) realistic?
If not, what could have gone wrong?
73. The probability P percent of having an accident while driv-
ing a car is related to the alcohol level of the driver’s blood
by the formula P e
kt
, where k is a constant. Accident sta-
tistics show that the probability of an accident is 25% when
the blood alcohol level is t .15.
(a) Find k. [Use P 25, not .25.]
(b) At what blood alcohol level is the probability of having
an accident 50%?
74. Under normal conditions, the atmospheric pressure (in mil-
libars) at height h feet above sea level is given by P(h)
1015e
kh
, where k is a positive constant.
(a) If the pressure at 18,000 feet is half the pressure at sea
level, find k.
(b) Using the information from part (a), find the atmo-
spheric pressure at 1000 feet, 5000 feet, and 15,000
feet.
75. One hour after an experiment begins, the number of bacte-
ria in a culture is 100. An hour later, there are 500.
(a) Find the number of bacteria at the beginning of the
experiment and the number three hours later.
(b) How long does it take the number of bacteria at any
given time to double?
76. If the population at time t is given by S(t) ce
kt
, find a for-
mula that gives the time it takes for the population to double.
408 CHAPTER 5 Exponential and Logarithmic Functions
77. The spread of a flu virus in a community of 45,000 people
is given by the function
f(t)
1
4
2
5
2
,0
4
0
e
0
.899t
,
where f(t) is the number of people infected in week t.
(a) How many people had the flu at the outbreak of the
epidemic? After three weeks?
(b) When will half the town be infected?
78. The beaver population near a certain lake in year t is
approximately
p(t)
1 1
2
9
0
9
0
e
0
.5544t
.
(a) When will the beaver population reach 1000?
(b) Will the population ever reach 2000? Why?
79. Assume that you watched 1000 hours of television this year,
and will watch 750 hours next year, and will continue to
watch 75% as much every year thereafter.
(a) In what year will you be down to ten hours per year?
(b) In what year would you be down to one hour per year?
80. In the year 2009, Olivia’s bank balance is $1000. In the
year 2010, her balance is $1100.
(a) If her balance is growing exponentially, in what
year will it reach $2500?
(b) If her balance is instead growing linearly, in what
year will it reach $2500?
THINKERS
81. According to one theory of learning, the number of words
per minute N that a person can type after t weeks of practice
is given by N c(1 e
kt
), where c is an upper limit that
N cannot exceed and k is a constant that must be determined
experimentally for each person.
(a) If a person can type 50 wpm (words per minute) after
four weeks of practice and 70 wpm after eight weeks,
find the values of k and c for this person. According to
the theory, this person will never type faster than
c wpm.
(b) Another person can type 50 wpm after four weeks of
practice and 90 wpm after eight weeks. How many
weeks must this person practice to be able to type
125 wpm?
82. Kate has been offered two jobs, each with the same starting
salary of $32,000 and identical benefits. Assuming satisfac-
tory performance, she will receive a $1600 raise each year
at the Great Gizmo Company, whereas the Wonder Widget
Company will give her a 4% raise each year.
(a) In what year (after the first year) would her salary be the
same at either company? Until then, which company
pays better? After that, which company pays better?
(b) Answer the questions in part (a) assuming that the
annual raise at Great Gizmo is $2000.
*U.S. Census Bureau, International Data Base.
†
www.census.gov
SECTION 5.6 Exponential, Logarithmic, and Other Models 409
5.6 Exponential, Logarithmic, and Other Models*
■ Determine the best type of function to model a set of data.
■ Find a reasonable model for a set of data.
Many data sets can be modeled by suitable exponential, logarithmic, and related
functions. Most calculators have regression procedures for constructing the fol-
lowing models.
We begin by examining exponential models, such as y 3
2
x
. A table of
values for this model is shown below. Look carefully at the ratio of successive
entries (that is, each entry divided by its predecessor).
It should not be a surprise that the ratio of successive entries is constant. For at
each step, x changes from x to x 4 (from 0 to 4, from 4 to 8, and so on) and y
changes from 3
2
x
to 3
2
x4
. Hence, the ratio of successive terms is always
2
4
16.
A similar argument applies to any exponential model y ab
x
and shows that
if x changes by a fixed amount k, then the ratio of the corresponding y values is the
constant b
k
(in our example b was 2 and k was 4). This suggests that
when the ratio of successive, equally spaced, entries in a table of data is
approximately constant, an exponential model is appropriate.
3
2
x
2
4
3
2
x
3
2
x4
3
2
x
Section Objectives
Model Equation Examples
Power y ax
r
y 5x
2.7
y 3.5x
.045
Exponential y ab
x
or y ae
kx
y 2(1.64)
x
y 2
e
.4947x
Logistic y
1
a
be
kx
y
1
20
2
,
4
0
e
0
0
.25x
y
1
65
6
0
e
.3x
Logarithmic y a b ln xy 5 4.2 ln xy 2 3 ln x
xy 3
⭈
2
x
03
4
3
8
16
448
7
4
6
8
8
16
8 768
12
7
,
6
2
8
88
16
12 12,288
1
1
9
2
6
,
,
2
6
2
0
8
8
16
16 196,608
*This section is optional; its prerequisites are Section 2.5 and Special Topics 4.4.A. It will be used in
clearly identifiable exercises but not elsewhere in the text.
EXAMPLE 1
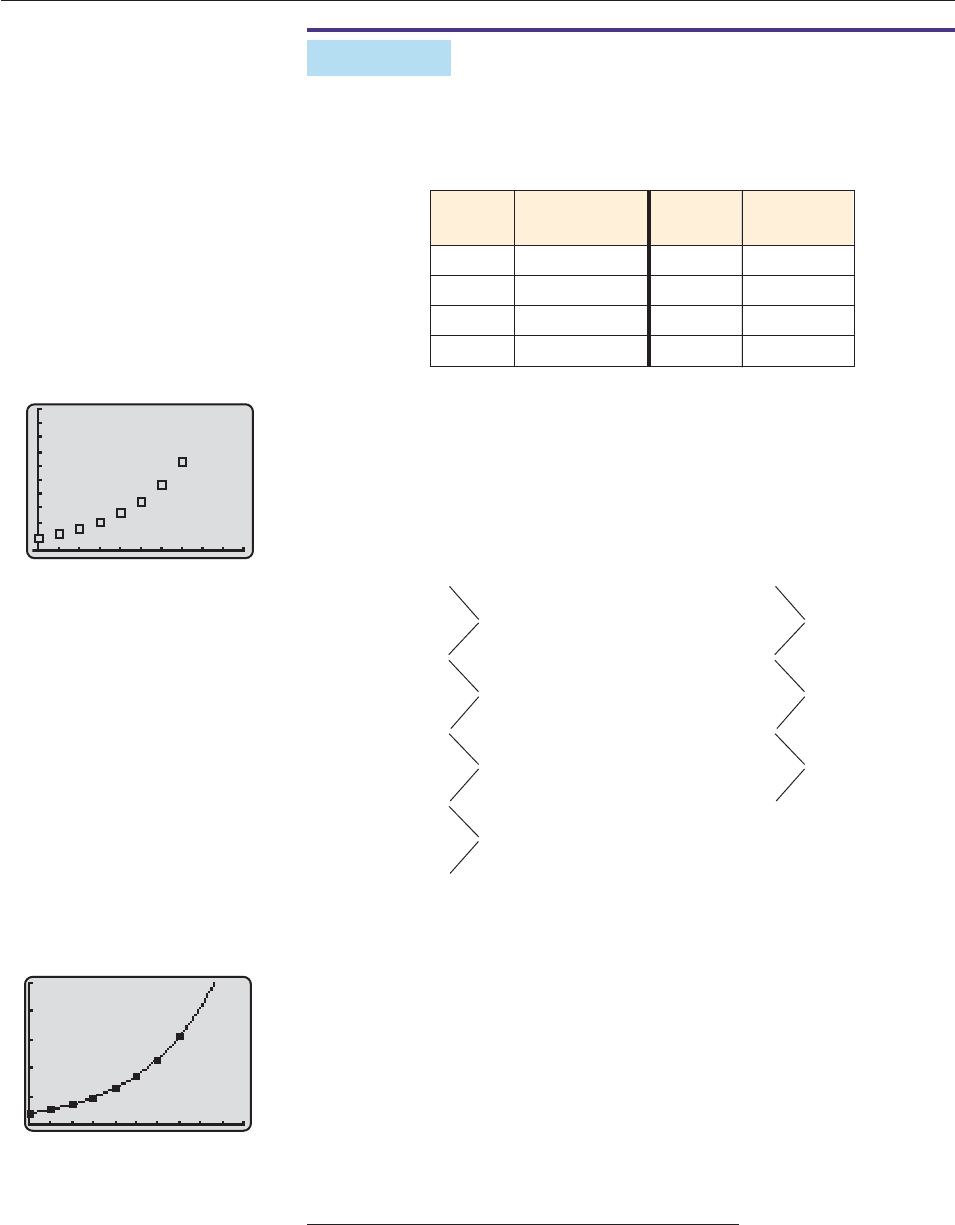
In the years before the Civil War, the population of the United States grew rapidly,
as shown in the following table from the U.S. Bureau of the Census. Find a model
for this growth.
SOLUTION The data points (with x 0 corresponding to 1790) are shown in
Figure 5–30. Their shape suggests either a polynomial graph of even degree or an
exponential graph. Since populations generally grow exponentially, an exponen-
tial model is likely to be a good choice. We can confirm this by looking at the
ratios of successive entries in the table.
Year Population Year Population
1790 3.93 1830 12.86
5
3
.
.
3
9
1
3
1.351
1
1
7
2
.
.
0
8
7
6
1.327
1800 5.31 1840 17.07
7
5
.
.
2
3
4
1
1.363
2
1
3
7
.
.
1
0
9
7
1.359
1810 7.24 1850 23.19
9
7
.
.
6
2
4
4
1.331
3
2
1
3
.
.
4
1
4
9
1.356
1820 9.64 1860 31.44
1
9
2
.
.
6
8
4
6
1.334
1830 12.86
The ratios are almost constant, as they would be in an exponential model. So we
use regression to find such an exponential model. The procedure is the same as for
linear and polynomial regression (see the Tips on pages 128 and 283). It produces
this model:*
y 3.9572 (1.0299
x
).
The graph in Figure 5–31 appears to fit the data quite well. In fact, you can
readily verify that the model has an error of less than 1% for each of the data
points. Furthermore, as discussed before the example, when x changes by 10, the
value of y changes by approximately 1.0299
10
1.343, which is very close to the
successive ratios of the data that were computed above. ■
410 CHAPTER 5 Exponential and Logarithmic Functions
Population Population
Year in Millions Year in Millions
1790 3.93 1830 12.86
1800 5.31 1840 17.07
1810 7.24 1850 23.19
1820 9.64 1860 31.44
−5
100
0
50
Figure 5–30
−5
100
0
50
Figure 5–31
*Throughout this section, coefficients are rounded for convenient reading, but the full expansion is
used for calculations and graphs.
EXAMPLE 2
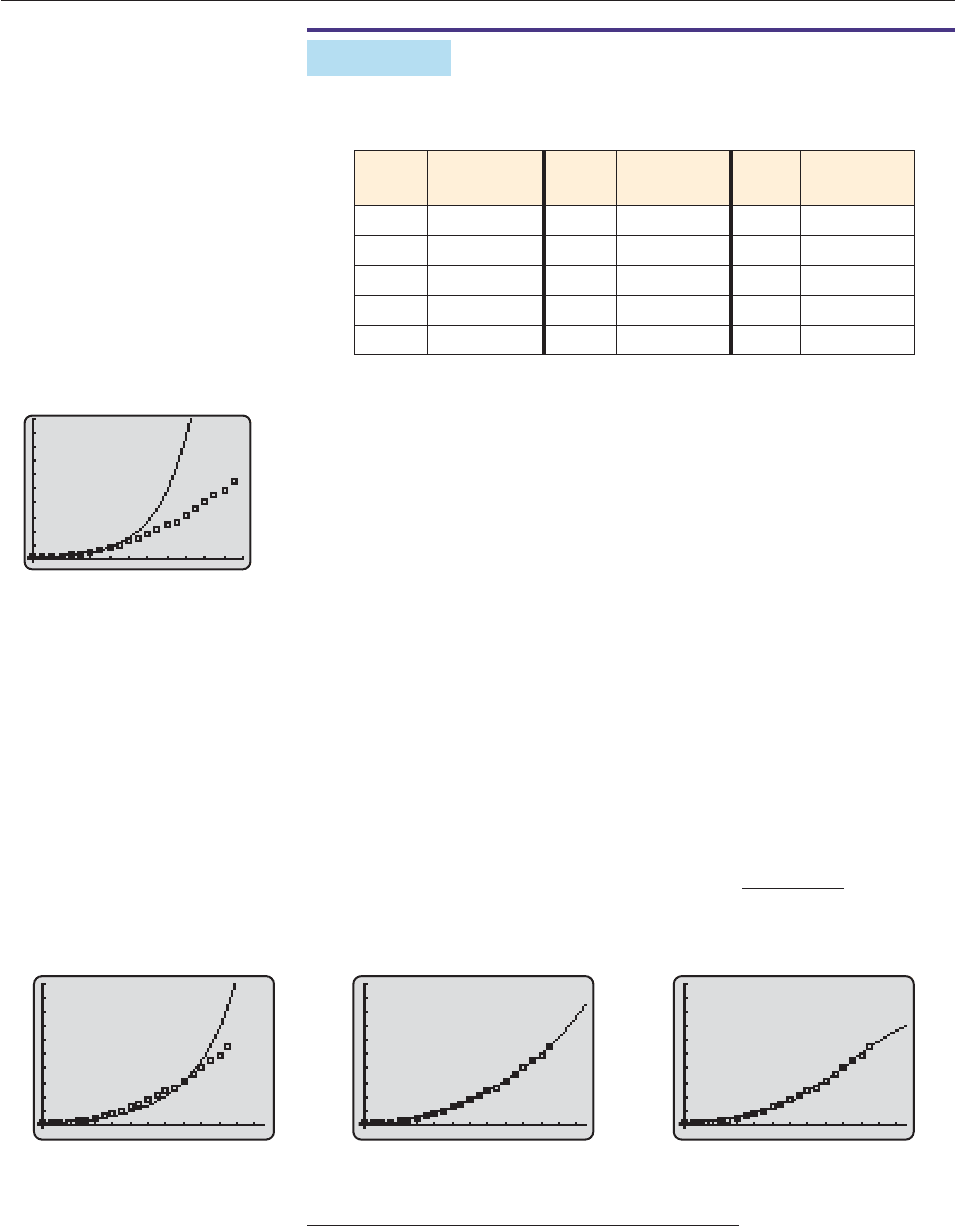
After the Civil War, the U.S. population continued to increase, as shown below.
However, the model from Example 1 does not remain valid, as can be seen in
Figure 5–32, which shows its graph together with all the data points from
1790 through 2000 (x 0 corresponds to 1790).
The problem is that the rate of growth has steadily decreased since the Civil
War. For instance, the ratio of the first two entries in the preceding table is
5
3
0
8
.
.
1
5
9
6
1.302,
and the ratio of the last two is
2
2
8
4
1
8
.
.
4
7
2
2
1.13.
So an exponential model may not be the best choice now. Other possibilities are
polynomial models (which grow at a slower rate) or logistic models (in which the
growth rate decreases with time). Figure 5–33 shows three possible models, each
obtained by using the appropriate regression program on a calculator, with all the
data points from 1790 through 2000.
Figure 5–33
500
0
y = 6.06616⋅1.02039
x
Exponential Model
250
−5
500
0
y = (7.94 × 10
−8
)x
4
− (2.76 × 10
−5
)x
3
+ .0093x
2
− .1621x + 5.462
Polynominal Model
250
−5
500
0
y =
1 + 56.33e
−.0216x
442.1
Logistic Model*
250
−5
SECTION 5.6 Exponential, Logarithmic, and Other Models 411
Population Population Population
Year in Millions Year in Millions Year in Millions
1870 38.56 1920 106.02 1960 179.32
1880 50.19 1930 123.20 1970 202.30
1890 62.98 1940 132.16 1980 226.54
1900 76.21 1950 151.33 1990 248.72
1910 92.23 2000 281.42
500
0
220
−5
Figure 5–32
*This model was obtained on a TI-83. Other calculators may produce a slightly different model or an
error message.
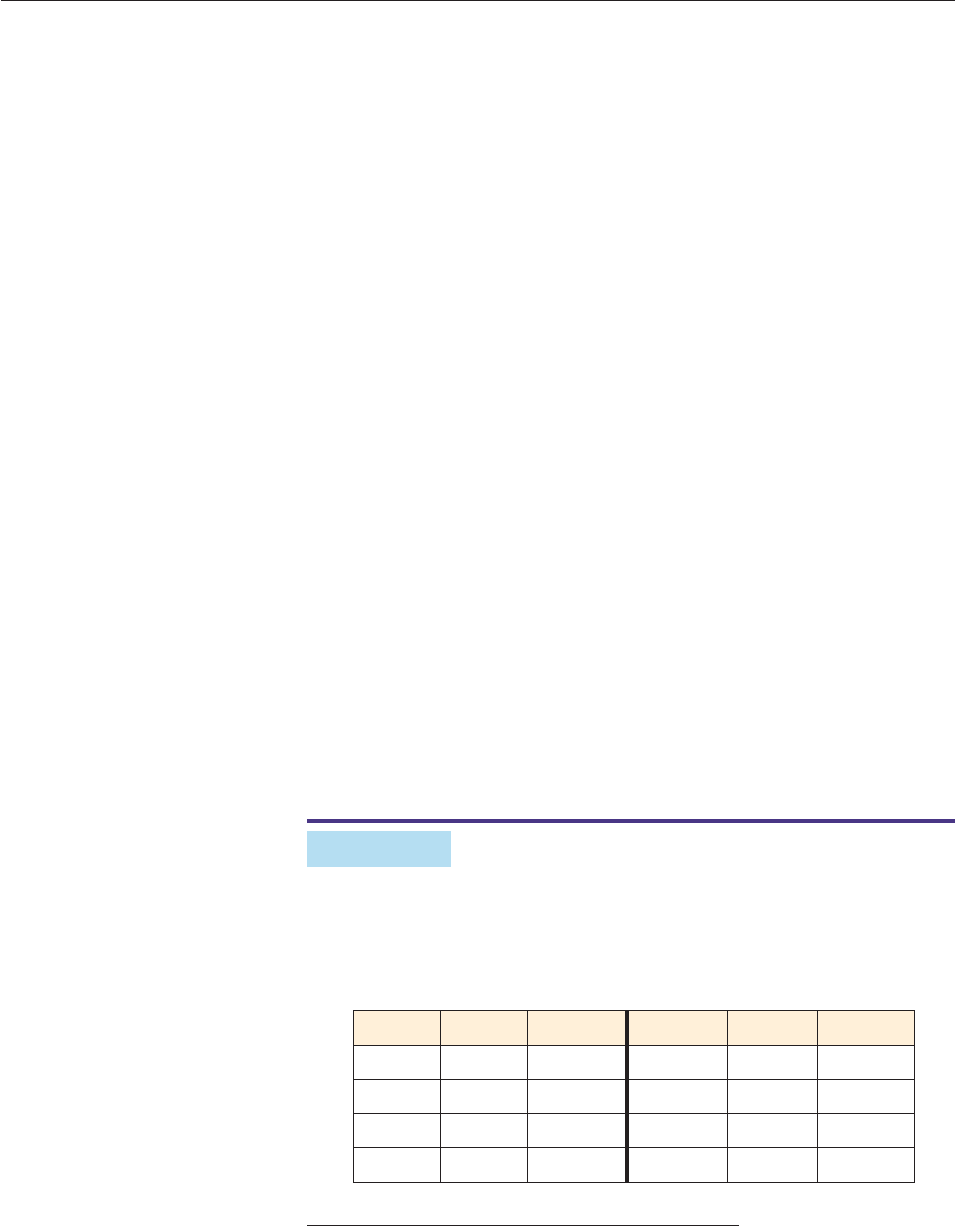
As expected, the polynomial and logistic models fit the data better than does the
exponential model. The main difference between them is that the polynomial
model indicates unlimited future growth, whereas the logistic model has the
population growing more slowly in the future (and eventually leveling off—see
Exercise 13). ■
In Example 1, we used the ratios of successive entries of the data table to
determine that an exponential model was appropriate. Here is another way to
make that determination. Consider the exponential function y ab
x
. Taking
natural logarithms of both sides and using the logarithm laws on the right side
shows that
ln y ln (ab
x
) ln a ln b
x
ln a x ln b.
Now ln a and ln b are constants, say, k ln a and m ln b, so
ln y mx k.
Thus, the points (x, ln y) lie on the straight line with slope m and y-intercept k.
Consequently, we have this guideline.
If (x, y) are data points and if the points (x, ln y) are approximately
linear, then an exponential model may be appropriate for the data.
Similarly, if y ax
r
is a power function, then
ln y ln (ax
r
) ln a r ln x.
Since ln a is a constant, say k ln a, we have
ln y r ln x k,
which means that the points (ln x, ln y) lie on a straight line with slope r and
y-intercept k. Consequently, we have this guideline.
If (x, y) are data points and if the points (ln x, ln y) are approximately
linear, then a power model may be appropriate for the data.
EXAMPLE 3
The length of time that a planet takes to make one complete rotation around the
sun is its year. The table shows the length (in earth years) of each planet’s year and
the distance of that planet from the sun (in millions of miles).* Find a model for
this data in which x is the length of the year and y the distance from the sun.
412 CHAPTER 5 Exponential and Logarithmic Functions
*Since the orbit of a planet around the sun is not circular, its distance from the sun varies through the
year. Each given number is the average of its maximum and minimum distances from the sun.
Planet Year Distance Planet Year Distance
Mercury .24 36.0 Jupiter 11.86 483.6
Venus .62 67.2 Saturn 29.46 886.7
Earth 1 92.9 Uranus 84.01 1783.0
Mars 1.88 141.6 Neptune 164.79 2794.0
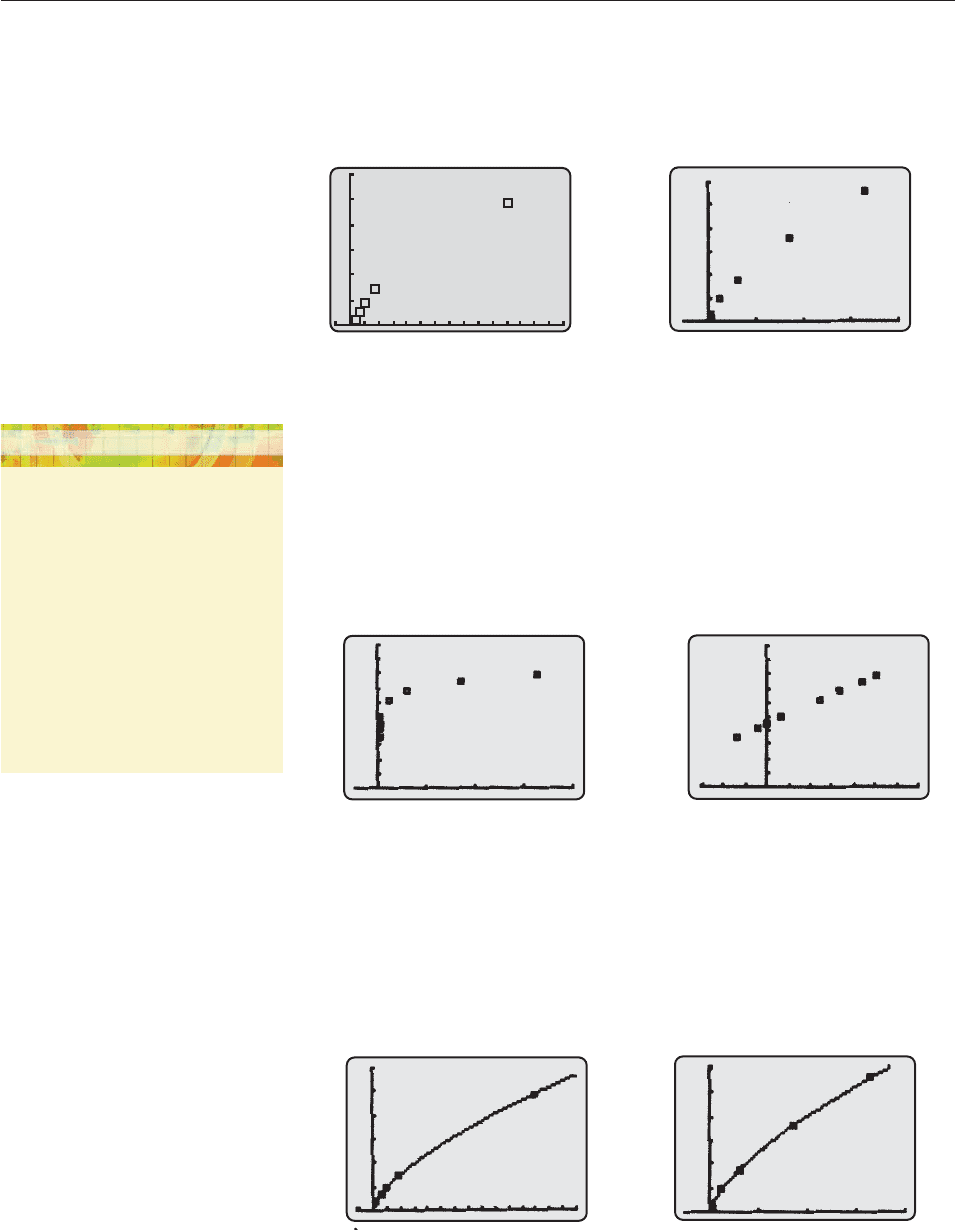
SOLUTION Figure 5–34 shows the data points for the five planets with the
shortest years. Figure 5–35 shows all the data points, but on this scale, the first
four points look like a single large one near the origin.
Figure 5–34 Figure 5–35
Plotting the point (x, ln y) for each data point (x, y) (see the Technology Tip in the
margin) produces Figure 5–36. Its points do not form a linear pattern (four of
them are almost vertical near the y-axis and the other five almost horizontal), so
an exponential function is not an appropriate model. On the other hand, the points
(ln x, ln y) in Figure 5–37 do form a linear pattern, which suggests that a power
model will work.
Figure 5–36 Figure 5–37
A calculator’s power regression feature produces this model.
y 92.8982 x
.6668
.
Its graph in Figure 5–38 shows that it fits the original data points quite well. ■
Figure 5–38
3,000
0
25
200
600
0
115
10
0
37
10
0
25 200
3,000
0
25 200
−1
15
0
600
SECTION 5.6 Exponential, Logarithmic, and Other Models 413
TECHNOLOGY TIP
Suppose the x- and y-coordinates of
the data points are stored in lists L
1
and L
2
, respectively. On calculators
other than TI-89, keying in
ln L
2
STO L
4
produces the list L
4
, whose entries are
the natural logarithms of the numbers
in list L
2
, and stores it in the statistics
editor. You can then use lists L
1
and L
4
to plot the points (x, ln y). For TI-89,
check your instruction manual.
If y a b ln x is a logarithmic model, then the points (ln x, y) lie on
the straight line with slope b and y-intercept a (why?). Thus, we have this
guideline.
If (x, y) are data points and if the points (ln x, y) are approximately
linear, then a logarithmic model may be appropriate for the data.
EXAMPLE 4
Find a model for population growth in El Paso, Texas, given the following data.*
SOLUTION The scatter plot of the data points (with x 50 corresponding to
1950) in Figure 5–39 bends slightly, suggesting a logarithmic curve. So we plot
the points (ln x, y), that is,
(ln 50, 130485), (ln 70, 322261), . . . , (ln 105, 598590),
in Figure 5–40. Since these points lie approximately on a straight line, a logarith-
mic model is appropriate. Using logarithmic regression on a calculator, we obtain
this model.
2,380,341.254 640,178.5447 ln x.
Its graph in Figure 5–41 is a good fit for the data. ■
Figure 5–39 Figure 5–40 Figure 5–41
700,000
0
40 120
700,000
0
3 6
700,000
0
40 120
414 CHAPTER 5 Exponential and Logarithmic Functions
There are three dwarf-planets in our solar system—Ceres, Pluto, and Eris. From its
discovery in 1930 until 2006, Pluto was considered a planet. The length of Pluto’s
year is 247.69 Earth years, and it is 3674.5 million miles from the sun. Does Pluto fit
the model we found using the 8 planets?
GRAPHING EXPLORATION
*U.S. Bureau of the Census.
Year 1950 1970 1980 1990 2000 2005
Population 130,485 322,261 425,259 515,342 563,662 598,590
CAUTION
When using logarithmic models, you
must have data points with positive
first coordinates (since logarithms of
negative numbers and 0 are not
defined).
SECTION 5.6 Exponential, Logarithmic, and Other Models 415
EXERCISES 5.6
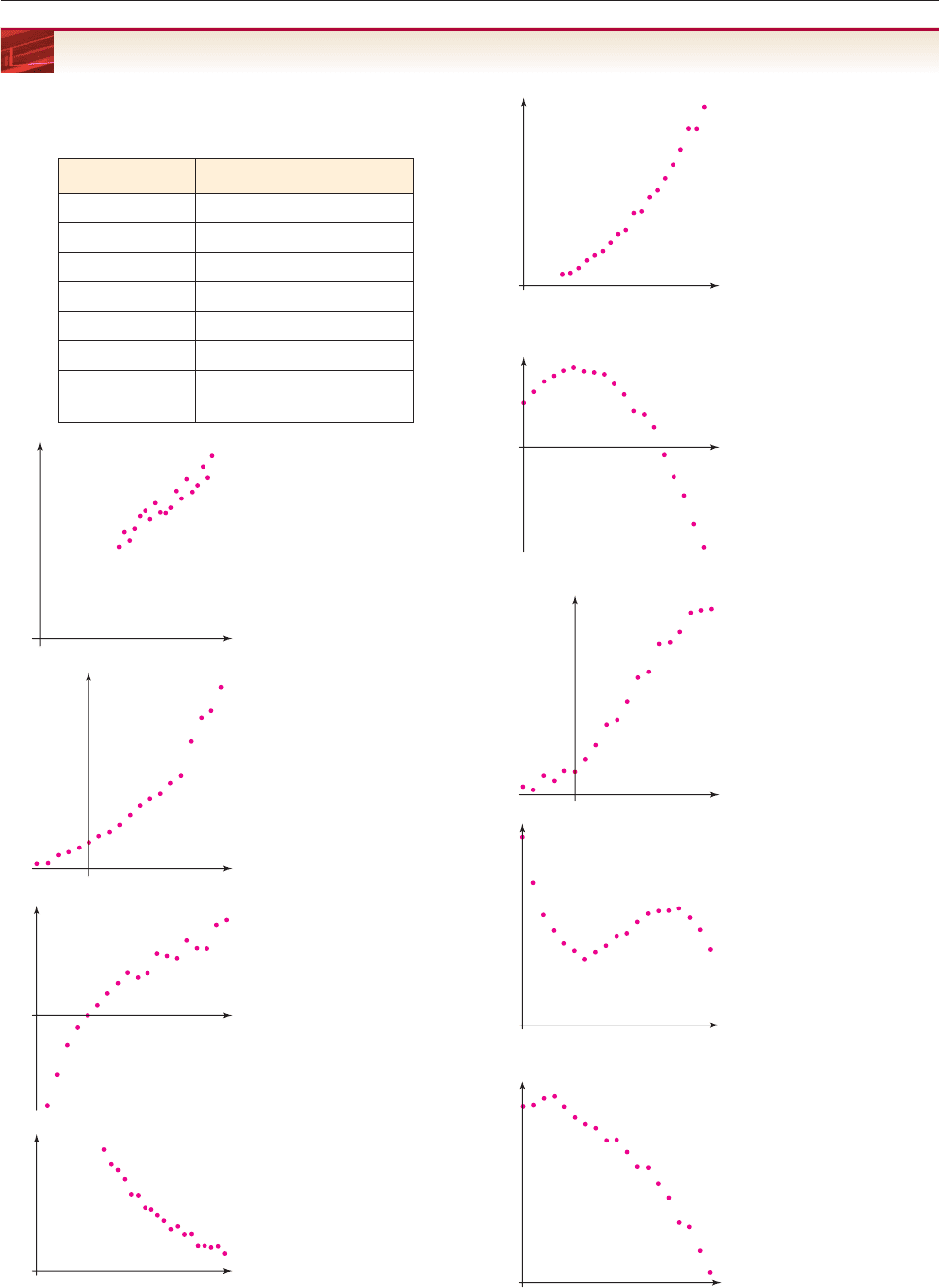
In Exercises 1–10, state which of the following models might be
appropriate for the given scatter plot of data (more than one
model may be appropriate).
1.
2.
3.
4.
x
y
x
y
x
y
y
x
5.
6.
7.
8.
9.
x
y
x
y
x
y
x
y
x
y
Model Corresponding Function
A. Linear y ax b
B. Quadratic y ax
2
bx c
C. Power y ax
r
D. Cubic y ax
3
bx
2
cx d
E. Exponential y ab
x
F. Logarithmic y a b ln x
G. Logistic y
1
a
be
kx
