Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

336 CHAPTER 4 Polynomial and Rational Functions
altitude h(t) of the rocket above the ground at given time
t is given by h(t) 10 112t 16t
2
(where h(t) is meas-
ured in feet).
(a) What is the altitude of the rocket the instant it is
launched?
(b) What is the altitude of the rocket 2 seconds after
launching?
(c) What is the maximum altitude attained by the rocket?
(d) At what time does the rocket return to the altitude at
which it was launched?
9. A rectangular garden next to a building is to be fenced with
120 feet of fencing. The side against the building will not be
fenced. What should the lengths of the other three sides be
to ensure the largest possible area?
10. A factory offers 100 calculators to a retailer at a price of $20
each. The price per calculator on the entire order will be
reduced 5¢ for each additional calculator over 100. What
number of calculators will produce the largest possible sales
revenue for the factory?
11. Which of the following are polynomials?
(a) 2
3
x
2
(b) x
1
x
(c) (2
)x
3
2x
2
1 (d)
x
1
1
2
0
0
3x
6
1
0
0
(e)
5
2x
8
(f) px 2p
3
(g) 3x
3
2x
2
1
2
x
1/2
1 (h) x x
12. What is the remainder when x
4
3x
3
1 is divided by
x
2
1?
13. What is the remainder when
x
112
2x
8
9x
5
4x
4
x 5
is divided by x 1?
14. Is x 1 a factor of f (x) 14x
87
65x
56
51? Justify your
answer.
15. Use synthetic division to show that x 2 is a factor of
x
6
5x
5
8x
4
x
3
17x
2
16x 4 and find the other
factor.
16. List the roots of the following polynomials and the multi-
plicities of each root:
(a) f(x) p (x 1)
3
(x
2
9)
2
(x 2)
(b) g(x) x
4
8x
3
18x
2
27 [Hint: Try computing
g(1).]
17. Find a polynomial f of degree 3 such that f(1) 0, f(1)
0, and f(0) 5.
18. Find the root(s) of 2
5
x
7
3x
x
5
2
4.
19. Find the roots of 3x
2
2x 5.
20. Factor the polynomial x
3
8x
2
9x 6. [Hint: 2 is a root.]
21. Find all real roots of x
6
4x
3
4.
22. Find all real roots of 9x
3
6x
2
35x 26. [Hint: Try
x 2].
23. Find all real roots of 3y
3
( y
4
y
2
5).
24. Find the rational roots of x
4
2x
3
4x
2
1.
25. Consider the polynomial 2x
3
8x
2
5x 3.
(a) List the only possible rational roots.
(b) Find one rational root.
(c) Find all the roots of the polynomial.
26. (a) Find all rational roots of x
3
2x
2
2x 2.
(b) Find two consecutive integers such that an irrational
root of x
3
2x
2
2x 2 lies between them.
27. How many distinct real roots does x
3
4x have?
28. How many distinct real roots does f(x) x
3
x
2
3x 3
have?
29. Find the roots of x
4
11x
2
18.
30. The polynomial x
3
2x 1 has
(a) no real roots. (d) only one rational root.
(b) only one real root. (e) none of the above.
(c) three rational roots.
31. Show that 5 is an upper bound for the real roots of
x
4
4x
3
16x 16.
32. Show that 1 is a lower bound for the real roots of
x
4
4x
3
15.
In Questions 33 and 34, find the real roots of the polynomial.
33. x
6
2x
5
x
4
3x
3
x
2
x 1
34. x
5
5x
4
8x
3
5x
2
13x 30
In Questions 35 and 36, compute and simplify the difference
quotient of the function.
35. f (x) x
2
x 36. g(x) 3x
3
2
37. Draw the graph of a function that could not possibly be the
graph of a polynomial function and explain why.
38. Draw a graph that could be the graph of a polynomial func-
tion of degree 5. You need not list a specific polynomial, nor
do any computation.
39. Which of the statements (a)–(c) is not true about the poly-
nomial function f whose graph is shown in the figure?
(a) f has three roots between 2 and 3.
(b) f (x) could possibly be a fifth-degree polynomial.
(c) ( f f )(0) 0.
(d) f (2) f (1) 3.
(e) f (x) is positive for all x in the interval [1, 0].
x
y
−2 −1−3 123
−1
−2
1
3
2
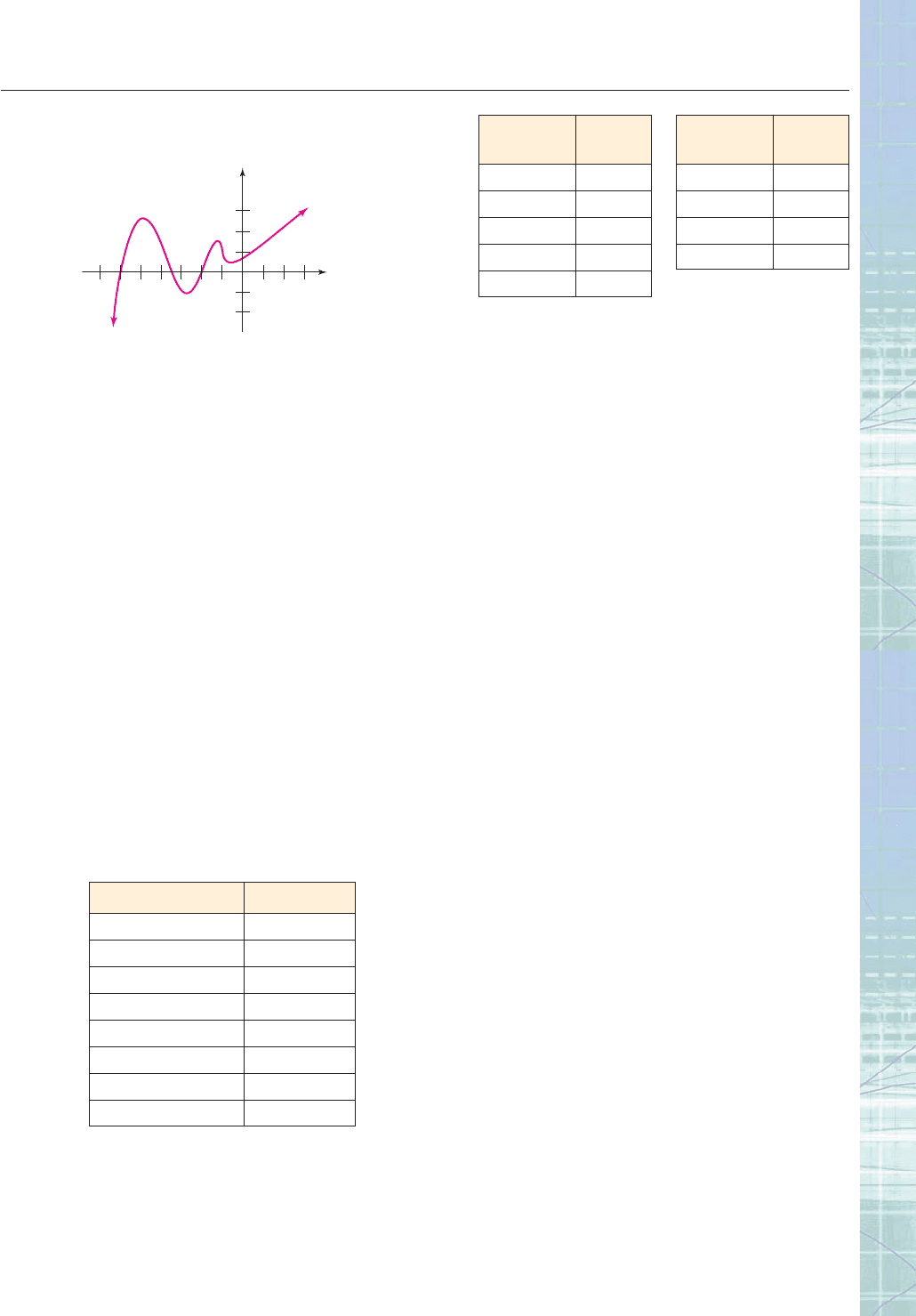
40. Which of the statements (i)–(v) about the polynomial func-
tion f whose graph is shown in the figure are false?
(i) f has 2 roots in the interval [6, 3).
(ii) f(3) f (6) 0.
(iii) f (0) f (1).
(iv) f (2) 2 0.
(v) f has degree 4.
In Questions 41–44, find a viewing window (or windows) that
shows a complete graph of the function. Be alert for hidden
behavior.
41. f (x) 32x
3
99x
2
100x 2
42. g(x) .3x
5
4x
4
x
3
4x
2
5x 1
43. h(x) 4x
3
100x
2
600x
44. f (x) x
7
11x
6
50x
5
120x
4
160x
3
112x
2
32x
45. HomeArt makes plastic replicas of famous statues. Their
total cost to produce copies of a particular statue are shown
in the table below.
(a) Make a scatter plot of the data.
(b) Use cubic regression to find a function C(x) that models
the data [that is, C(x) is the cost of making x statues].
Assume that C is reasonably accurate when x 100.
(c) Use C to estimate the cost of making the seventy-first
statue.
(d) Use C to approximate the average cost per statue when
35 are made and when 75 are made. [Recall that the
average cost of x statues is C(x)/x.]
46. The table gives the estimated cost of a college education at a
public institution. Costs include tuition, fees, books, and
room and board for four years. (Source: Teachers Insurance
and Annuity Association College Retirement Equities Fund)
x
y
−2 −1−3−5 −4−6−7123
−2
−4
2
6
4
CHAPTER 4 Review 337
(a) Make a scatter plot of the data (with x 0 correspon-
ding to 1990).
(b) Use quartic regression to find a function C that models
the data.
(c) Estimate the cost of a college education in 2007 and in
2015.
In Questions 47–54, sketch a complete graph of the function.
Label the x-intercepts, all local extrema, holes, and asymptotes.
47. f(x) x
3
9x 48. g(x) x
3
2x
2
3
49. h(x) x
4
3x
3
12x
2
20x 48
50. f(x) x
4
3x 2
51. g(x)
x
2
4
52.
3
x
x
3
3
3
2
x
x
2
2
2
8
x
x
53. k(x)
4
3
x
x
1
9
0
54. f(x)
x
x
2
1
1
In Questions 55 and 56, list all asymptotes of the graph of the
function.
55. f(x)
x
3
2
x
x
2
2
1
5x 6
56. g(x)
In Questions 57–60, find a viewing window (or windows) that
shows a complete graph of the function. Be alert for hidden
behavior.
57. f (x)
x
2
x
x
3
2
58. g(x)
x
3
x
2
3x
2
x
3x
6
1
59. h(x)
x
4
x
9
4
9x
2
4
100
60. k(x)
x
3
2
x
x
2
10
4x 8
61. It costs the Junkfood Company 50¢ to produce a
bag of Munchies. There are fixed costs of $500 per day for
building, equipment, etc. The company has found that if the
price of a bag of Munchies is set at 1.95
20
x
00
dollars,
where x is the number of bags produced per day, then all the
bags that are produced will be sold. What number of bags
can be produced each day if all are to be sold and the com-
pany is to make a profit? What are the possible prices?
x
4
6x
3
2x
2
6x 2
x
2
3
Number of Statues Total Cost
0 $2,000
10 2,519
20 2,745
30 2,938
40 3,021
50 3,117
60 3,269
70 3,425
Enrollment
Year Costs
1998 $46,691
2000 52,462
2002 58,946
2004 66,232
2006 74,418
Enrollment
Year Costs
2008 $83,616
2010 93,951
2012 105,564
2014 118,611

338 CHAPTER 4 Polynomial and Rational Functions
62. Sunnyvale village is proud of its Main Street, which is a 33
mile long street running from the northernmost point of the
village to its southernmost point. There is a 3 mile long
stretch that goes through “Downtown Sunnyvale.” They
have a law that requires the speed limit through downtown
to be 15 miles/hour less than the speed limit everywhere
else.
(a) If the speed limit through downtown is 20 miles/hour,
how long does it take to get from the northernmost point
of Sunnyvale to its southernmost point?
(b) Express the total time for the north-to-south journey as
a function of the speed limit through downtown.
(c) The Sunnyvale Chamber of Commerce would like the
time for a trip through Sunnyvale to take 1.5 hours.
What would the downtown speed limit have to be for
this to be the case? Do you think the citizens of Sunny-
vale would agree to their proposal?
63. The survival rate s of seedlings in the vicinity of a parent
tree is given by
s
1
.5
.
x
4x
2
,
where x is the distance from the seedling to the tree (in
meters) and 0 x 10.
(a) For what distances is the survival rate at least .21?
(b) What distance produces the maximum survival rate?
In Questions 64 and 65, find the average rate of change of the
function between x and x h.
64. f(x)
x
x
1
65. g(x)
x
2
1
1
66. Which of these statements about the graph of
f(x)
(x
(x
2
1
1
)
)
(
(
x
x
2
3
1
)
)
is true?
(a) The graph has two vertical asymptotes.
(b) The graph touches the x-axis at x 3.
(c) The graph lies above the x-axis when x 1.
(d) The graph has a hole at x 1.
(e) The graph has no horizontal asymptotes.
67. Solve for x: 3(x 4) 5 x.
68. Solve for y:
y
3
2
5.
69. Solve for x: 4 2x 5 9.
70. On which intervals is
2
3
x
x
1
1
1?
71. On which intervals is
x
2
1
x?
72. Solve for x:
1
1
x
2
1
2
.
73. Solve for x: x
2
x 12.
74. Solve for x: (x 1)
2
(x
2
1)x 0.
75. If 0 r s t, then which of these statements is false?
(a) s r t (b) t s r
(c) r s t (d)
s
r
t
0
(e) s r t
76. Solve and express your answer in interval notation:
2x 3 5x 9 3x 4.
In Questions 77–84, solve the inequality.
77. 3x 2 2
78. x
2
x 20 0
79.
x
x
2
4
3
80. (x 1)
2
(x 3)
4
(x 2)
3
(x 7)
5
0
81.
x
2
x
x
3
9
1
82.
x
2
x
x
3
6
1
83.
x
2
x
2
x
2
5
2
84.
x
4
3
x
x
2
2
4
2x 3
1
In Questions 85–92, solve the equation in the complex number
system.
85. x
2
3x 10 0
86. x
2
2x 5 0
87. 5x
2
2 3x
88. 3x
2
4x 5 0
89. 3x
4
x
2
2 0
90. 8x
4
10x
2
3 0
91. x
3
8 0
92. x
3
27 0
93. One root of x
4
x
3
x
2
x 2 is i. Find all the roots.
94. One root of x
4
x
3
5x
2
x 6 is i. Find all the roots.
95. Give an example of a fourth-degree polynomial with real
coefficients whose roots include 0 and 1 i.
96. Find a fourth-degree polynomial f whose only roots are
2 i and 2 i, such that f (1) 50.
CHAPTER 4 Test 339
Chapter
4
Test
Sections 4.1–4.4 including Special Topics 4.2.A and 4.4.A.
1. An object moves back and forth along a straight track. Its
distance in meters from its starting point is given by the
function f(t) 15t
4
5t
2
6t
3
2t, where t is in minutes.
At what time does it return to its starting point?
2. State the quotient and remainder when the first polynomial
is divided by the second.
(a) x
3
5x
2
5x 7, x 4
(b) 2x
4
5x
3
2x
2
x 2, x 2
(c) x
5
2x
3
2x
4
5x
2
7x 3, x
2
3
3. Without using a calculator, match the following functions
with their graphs:
(a) f(x) (x 1)
2
2 (b) f (x) (x 1)
2
2
(c) f(x) (x 1)
2
2 (d) f(x) (x 1)
2
2
(e) f(x) (x 1)
2
2 (f) f(x) (x 1)
2
2
(g) f(x) (x 1)
2
2 (h) f (x) (x 1)
2
2
4. A mime troupe decides to start charging admission to their
performances. They figure that if they charge $10 per ticket,
they can sell 75 tickets. For every quarter decrease in price,
they can sell 5 more tickets. Conversely, for every quarter
increase in price, they can sell 5 fewer tickets.
(a) Write a function that gives their total income if they
charge $x for a ticket.
(b) What should they charge to make as much money as
possible?
5. Find all real roots of the following polynomials
(a) 3x
3
x
2
3x 1
(b) x
4
11x
2
18
(c) x
4
x
3
x
2
3x 6
Sections 4.5–4.8 including Special Topics 4.5.A and 4.6.A
6. Two positive numbers, x and y sum to 30. If xy 200, what
are the possible values of x? (x need not be an integer)
7. Solve the following equations and write the answers in the
form a bi
(a) 2x 3 4i 3x 6 2i
(b) x
2
4x 13 0
(c) 4 x
2
5x
2
5
8. Consider the following function: f(x)
x
2
x
2x
1
8
(a) Find the y intercept of this function
(b) List the vertical and horizontal asymptotes of this
function.
(c) Find the zeros of this function.
(d) Sketch a complete graph of this function.
9. Solve the following inequalities
(a) 3x 6 4 2x
(b) x
2
3x 2 0
(c)
3
x
x
2
1
x
1
2
(d) 2x 1 5
(e) 4x 6 12
10. Find the nonvertical asymptote of the following function,
and sketch its graph:
3x
2
x
3x
1
1
11. Find a 5th degree polynomial with real coefficients whose
roots include 1 2i, 5 i and 0. You may leave it in fac-
tored form if you choose.
x
y
−2 −11
5
10
−5
−10
23−3
x
y
−2−31
5
10
−5
−10
23−1
x
y
−2−3 −11
−5
5
10
−10
23
x
y
−2−3 −11
10
5
−5
−10
23
x
y
−2−3 −11
−5
10
5
−10
23
x
y
−2−3 −11
−5
10
5
−10
23
x
y
−2−3 −11
−5
10
5
−10
23
x
y
−2−3 −11
10
5
−5
−10
23

Mike Mazzaschi/Stock, Boston Inc. /PictureQuest
340
DISCOVERY PROJECT 4 Architectural Arches
You can see arches almost everywhere you look—in windows, entryways, tun-
nels, and bridges. Common arch shapes are semicircles, semiellipses, and parabo-
las. When constructed on a level base, arches are symmetric from left to right.
This means that a mathematical function that describes an arch must be an even
function.
A semicircular arch always has the property that its base is twice as wide as
its height. This ratio can be modified by placing a rectangular area under the semi-
circle, giving a shape known as a Norman arch. This approach gives a tunnel or
room a vaulted ceiling. Parabolic arches can also be created to give a more
vaulted appearance.
For the following exercises in arch modeling, you should always set the
origin of your coordinate system to be the center of the base of the arch.
1. Show that the function that models a semicircular arch of radius r is
h(x)
r
2
x
2
.
2. Write a function h(x) that models a semicircular arch that is 15 feet tall.
How wide is the arch?
3. Write a function n(x) that models a Norman arch that is 15 feet tall and
16 feet wide at the base.
4. Parabolic arches are typically modeled by using the function
p(x) H ax
2
,
where H is the height of the arch. Write a function p(x) for an arch that is
15 feet tall and 16 feet wide at the base.
5. Would a truck that is 12 feet tall and 9 feet wide fit through all three
arches? How could you fix any of the arches that is too small so that the
truck would fit through?
Semicircular Norman Parabolic

EXPONENTIAL AND LOGARITHMIC FUNCTIONS
How old is that dinosaur?
Population growth (of humans, fish, bacteria, etc.),
compound interest, radioactive decay, and a host of
other phenomena can be mathematically described by
exponential functions (see Exercises 52, 65 and 67 on
pages 366 and 368). Archeologists sometimes use
carbon-14 dating to determine the approximate age of
an artifact (such as a dinosaur skeleton, a mummy, or
a wooden statue). This involves using logarithms to
solve an appropriate exponential equation. See
Exercise 75 on page 369.
341
Chapter
© Rudi Von Briel/PhotoEdit
15,000
16
−6
−3000

342
Chapter Outline
Interdependence of
Sections
5.1 Radicals and Rational Exponents
5.1.A Special Topics: Radical Equations
5.2 Exponential Functions
5.2.A Special Topics: Compound Interest and the
Number e
5.3 Common and Natural Logarithmic Functions
5.4 Properties of Logarithms
5.4.A Special Topics: Logarithmic Functions to
Other Bases
5.5 Algebraic Solutions of Exponential and
Logarithmic Equations
5.6 Exponential, Logarithmic, and Other Models
Exponential and logarithmic functions provide mathematical models of
many natural and scientific phenomena. Technology is usually needed to
evaluate these functions, but the calculations can sometimes be done by
hand. Knowing the domains and ranges of these functions and the
unique shapes of their graphs is essential for understanding why these
functions are so common in nature.
5.1 Radicals and Rational Exponents
■ Find exact and approximate roots of real numbers.
■ Simplify expressions with rational exponents.
■ Interpret radical notation.
■ Rationalize numerators and denominators.
A square root of a nonnegative number c is a number whose square is c, that is,
a solution of x
2
c. For a real number c and a positive integer n, we define the
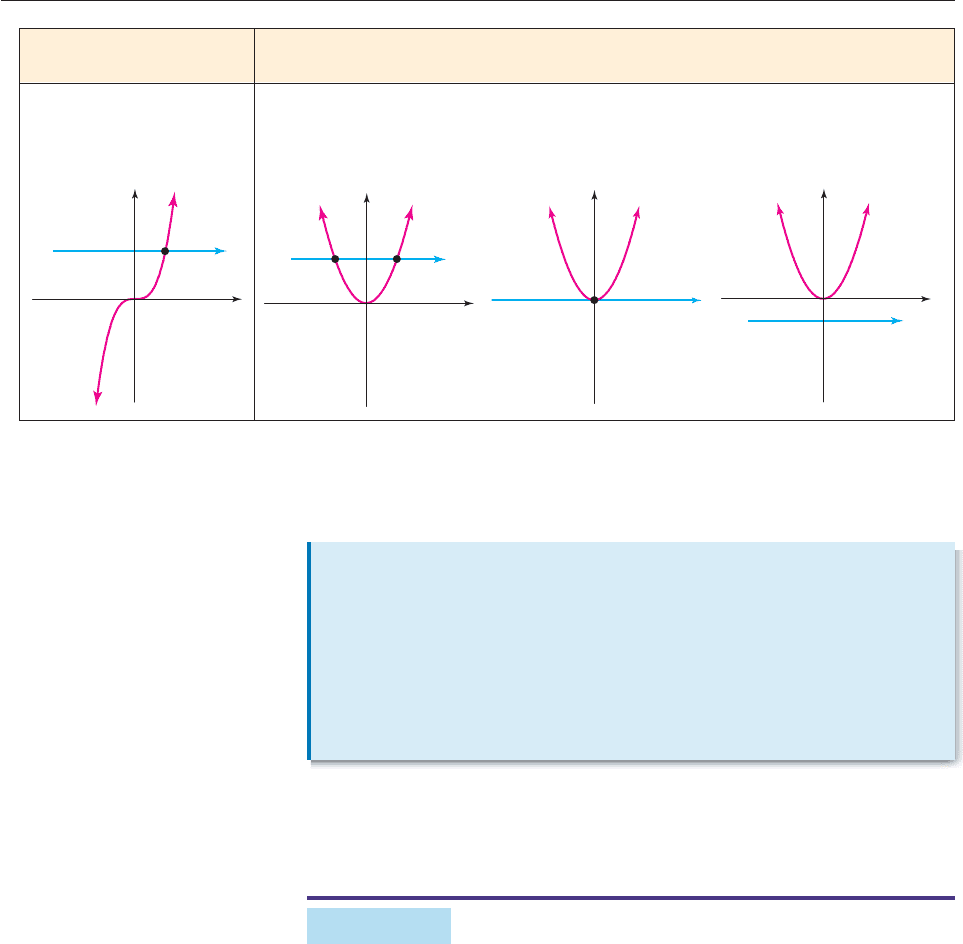
nth roots of c as the solutions of the equation x
n
c. The graphs on the next page
show that this equation may have two, one, or no solutions, depending on whether
n is even or odd and whether c is positive or negative.*
*The solutions of x
n
c are the x-coordinates of the intersection points of the graph of y x
n
and the
horizontal line y c. The graph of y x
n
was discussed on page 270.
Section Objectives
5.5
5.1 5.2 5.3 5.4
5.6
5.4.A can be covered
before 5.3 if desired.
SECTION 5.1 Radicals and Rational Exponents 343
Consequently, we have the following definition.
x
n
cx
n
c
n odd n even
x
y
c
y = c
y = x
n
x
y
c
y = c
y = x
n
x
y
y = 0
y = x
n
x
y
c
y = c
y = x
n
Exactly one c 0 c 0 c 0
solution for One positive and One solution No solution
any c one negative solution x 0
nth Roots
Let c be a real number and n a positive integer. The principal nth root of c
is denoted by either of the symbols
n
c
or c
1/n
and is defined to be
The solution of x
n
c, when n is odd;
The nonnegative solution of x
n
c, when n is even and c 0.
As before, principal square roots are denoted
rather than
2
.
EXAMPLE 1
Find the following roots.
(a)
3
8
(b) 81
1/4
(c)
5
32 (d)
1
4
SOLUTION
(a)
3
8
(8)
1/3
2 because 2 is the solution of x
3
8.
(b) 81
1/4
4
81 3 because 3 is the positive solution of x
4
81.
(c)
5
32 32
1/5
2 because 2 is the solution of x
5
32.
(d)
1
4
1
2
because
1
2
is the positive solution of x
2
1
4
. ■
344 CHAPTER 5 Exponential and Logarithmic Functions
Rational
Exponents
Let c be a positive real number and let t/k be a rational number in lowest
terms with positive denominator. Then,
c
t/k
is defined to be the number (c
t
)
1/k
(c
1/k
)
t
.
NOTE
The preceding definition is also valid when c is negative, provided that the exponent has an odd
denominator, such as (8)
2/3
(see Exercise 69). Nevertheless, if you try to compute (8)
2/3
on your
calculator, you may get an error message or a complex number (indicated by an ordered pair or an
expression involving i ) instead of the correct answer,
(8)
2/3
[(8)
2
]
1/3
3
(8)
2
3
64
4.
If this happens, you can probably get the correct answer by keying in either [(8)
2
]
1/3
or
[(8)
1/3
]
2
, each of which is equal to (8)
2/3
.
EXAMPLE 2
Use a calculator to approximate
(a) 40
1/5
(b) 225
1/11
SOLUTION
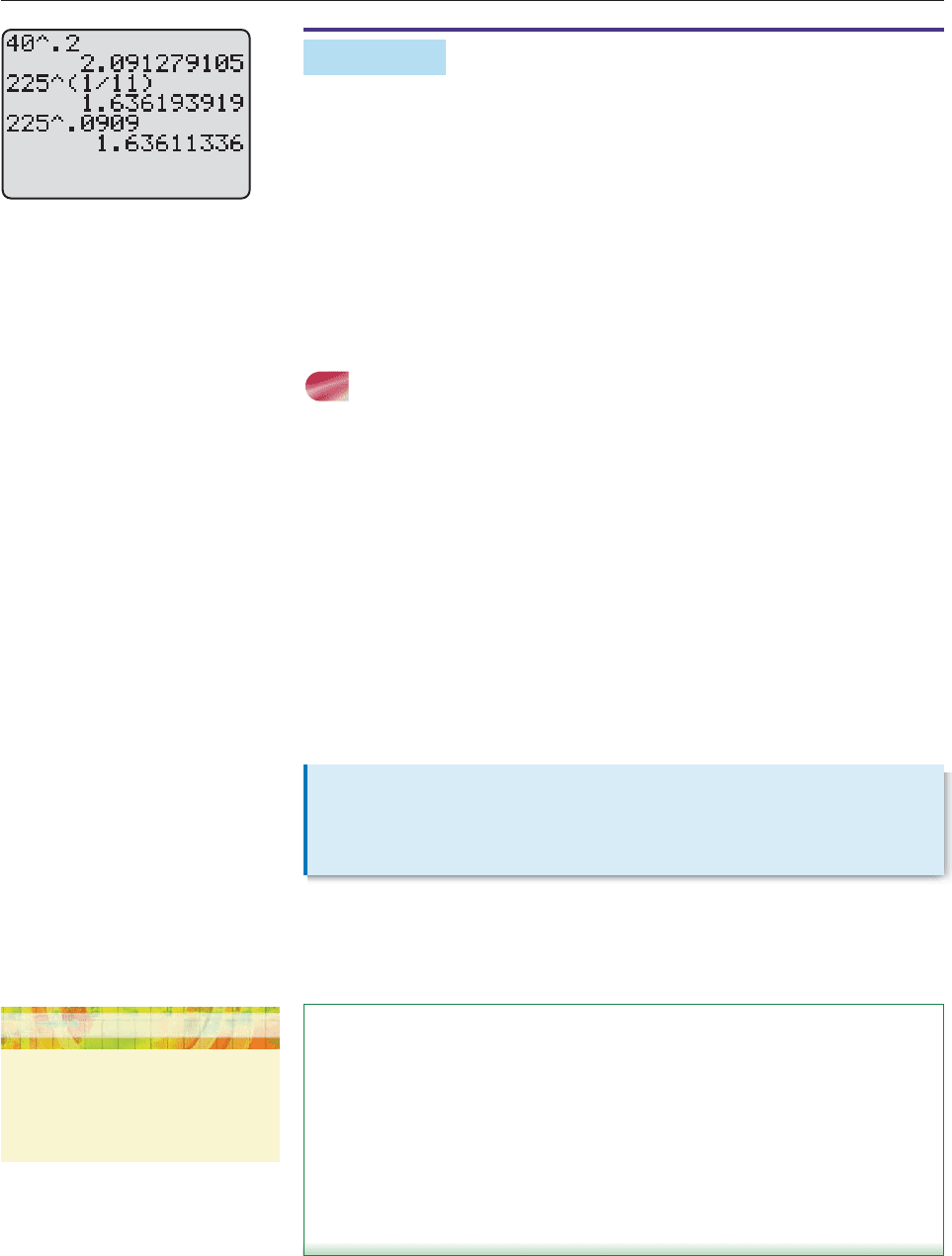
(a) Since 1/5 .2, you can compute 40
.2
, as in Figure 5–1.
(b) 1/11 is the infinite decimal .090909 . . . . In such cases, it is best to leave the
exponent in fractional form and use parentheses, as shown in Figure 5–1. If
you round off the decimal equivalent of 1/11, say as .0909, you will not get
the same answer, as Figure 5–1 shows. ■
RATIONAL EXPONENTS
The next step is to give a meaning to fractional exponents for any fraction, not just
those of the form 1/n. If possible, they should be defined in such a way that the
various exponent rules continue to hold. Consider, for example, how 4
3/2
might
be defined. The exponent 3/2 can be written as either
3
1
2
or
1
2
3.
If the power of a power property (c
m
)
n
c
mn
is to hold, we might define 4
3/2
as
either (4
3
)
1/2
or (4
1/2
)
3
. The result is the same in both cases:
(4
3
)
1/2
64
1/2
64 8 and (4
1/2
)
3
(4
)
3
2
3
8.
It can be proved that the same thing is true in the general case, which leads to this
definition.
Since every terminating decimal is a rational number, expressions such as
13
3.77
now have a meaning, namely, 13
377/100
. (Actually, we used this fact earlier
when we computed 40
.2
and 225
.0909
in Figure 5–1.)
TECHNOLOGY TIP
TI-89 will produce real number an-
swers to computations like (8)
2/3
if
you select “Real” in the COMPLEX
FORMAT submenu of the MODE menu.
Figure 5–1

Rational exponents were defined in a way that guaranteed that one of the
familiar exponent laws would remain valid. In fact, all exponent laws developed
for integer exponents are valid for rational exponents, as summarized here and
illustrated in Examples 3 through 5.
EXAMPLE 3
Compute the product x
1/2
(x
3/4
x
3/2
).
SOLUTION
Distributive law: x
1/2
(x
3/4
x
3/2
) x
1/2
x
3/4
x
1/2
x
3/2
Multiplication with exponents (law 1): x
1/23/4
x
1/23/2
1
2
3
4
5
4
and
1
2
3
2
2: x
5/4
x
2
. ■
EXAMPLE 4
Simplify (8r
3/4
s
3
)
2/3
, and express it without negative exponents.
SOLUTION
Product to a power (law 4): (8r
3/4
s
3
)
2/3
8
2/3
(r
3/4
)
2/3
(s
3
)
2/3
Power of a power (law 3): 8
2/3
r
(3/4)(2/3)
s
(3)(2/3)
3
4
2
3
1
2
and (3)
2
3
2: 8
2/3
r
1/2
s
2
Negative exponents (law 6):
8
2/
s
3
2
r
1/2
8
2/3
3
8
2
3
64 4:
4r
s
1
2
/2
or
4
s
2
r
. ■
EXAMPLE 5
Simplify
(
x
xy
7/
7
2
/
y
4
)
3
2
and express it without negative exponents.
SECTION 5.1 Radicals and Rational Exponents 345
Exponent
Laws
Let c and d be nonnegative real numbers, and let r and s be any rational
numbers. Then
1. c
r
c
s
c
rs
4. (cd)
r
c
r
d
r
2.
c
c
r
s
c
rs
(c 0) 5.
d
c
r
d
c
r
r
(d 0)
3. (c
r
)
s
c
rs
6. c
r
c
1
r
(c 0)
CAUTION
The exponent laws deal only with
products and quotients. There are no
analogous properties for sums. In
particular, if both c and d are nonzero,
then
(c d )
r
is not equal to
c
r
d
r
.
