Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

31. x
3
3x
2
x 3 0
32. x
4
14x
3
48x
2
0
33. x
4
5x
2
4 0
34. x
4
10x
2
9 0
35. 2x
4
3x
3
2x
2
4x 2
36. x
5
5x
4
4x
3
3x
2
2
37.
3
2
x
x
1
4
0 38.
2
x
x
2
2
4
x
x
1
4
0
39.
x
x
2
1
1 40.
2x
x
3
5
2
41.
x
2
3
x
1
1
42.
x
1
1
x
1
2
43. 3
44. 15
45.
2
2
x
x
2
2
6
5
x
x
8
3
1 [Be alert for hidden behavior.]
46.
x
2
1
x 6
x
x
2
3
x
x
3
2
In Exercises 47–48, solve the inequality using the method of
Example 9.
47. x(x 1)
3
(x 2)
4
0
48. x
4
5x
3
9x
2
7x 2 0
[Hint: First find the rational roots; then factor.]
In Exercises 49–51, read the solution of the inequality from the
given graph.
49. 3 2x .8x 7
50. 8 7 5x 3
10
10
−5
−10
(2.4, 3)
(.4, 3)
y = 8 –
|7 – 5x|
y = 3
8
5
−5
−
2
(–1.43, 5.86)
y = .8x + 7
y = 3 – 2x
x
4
3x
3
2x
2
2
x 2
x
3
3x
2
5x 29
x
2
7
316 CHAPTER 4 Polynomial and Rational Functions
51. x
2
3x 1 4
52. The graphs of the revenue and cost functions for a manu-
facturing firm are shown in the figure.
(a) What is the break-even point?
(b) Shade in the region representing profit.
(c) What does the y-intercept of the cost graph represent?
Why is the y-intercept of the revenue graph 0?
53. One freezer costs $723.95 and uses 90 kilowatt hours (kwh)
of electricity each month. A second freezer costs $600 and
uses 100 kwh of electricity each month. The expected life of
each freezer is 12 years. What is the minimum electric rate
(in cents per kwh) for which the 12-year total cost (purchase
price electricity costs) will be less for the first freezer?
54. A business executive leases a car for $300 per month. She
decides to lease another brand for $250 per month but has
to pay a penalty of $1000 for breaking the first lease. How
long must she keep the second car to come out ahead?
55. A sales agent is given a choice of two different compensa-
tion plans. The first plan has no salary, but a 10% commis-
sion on total sales. The second plan has a salary of $3000
per month, plus a 2% commission on total sales. What range
of monthly sales will make the first plan a better choice for
the sales agent?
56. A developer subdivided 60 acres of a 100-acre tract, leaving
20% of the 60 acres as a park. Zoning laws require that at
least 25% of the total tract be set aside for parks. For finan-
cial reasons, the developer wants to have no more than 30%
of the tract as parks. How many one-quarter-acre lots can
the developer sell in the remaining 40 acres and still meet
the requirements for the whole tract?
1000 2000
Revenue
Dollars
Cost
3000
Number of Items Produced
4000
20,000
40,000
60,000
10
5
−7
−2
(.79, 4)(–3.79, 4)
y = x
2
+ 3x + 1
y = 4

57. Emma and Aidan currently pay $60 per month for phone
service from AT&T. This fee gets them 900 minutes per
month. They look at their phone bills and realize that, at
most, they talk for 100 minutes per month. They find out
that they can go with Virgin Mobile and pay 18 cents per
minute. If they choose to switch services, they will have
to buy two new phones at $40 each, and pay a $175
“cancellation fee” to AT&T.
(a) Assuming that they talk for 100 minutes per month,
how many months would they have to talk before they
would be saving money?
(b) Assume they make the switch, and talk between zero
and 100 minutes per month. What is the range of possi-
ble savings?
58. How many gallons of a 12% salt solution should be added
to 10 gallons of an 18% salt solution to produce a solution
whose salt content is between 14% and 16%?
59. Find all pairs of numbers that satisfy these two conditions:
Their sum is 20, and the sum of their squares is less than 362.
60. The length of a rectangle is 6 inches longer than its width.
What are the possible widths if the area of the rectangle is
at least 667 square inches?
61. It costs a craftsman $5 in materials to make a medallion. He
has found that if he sells the medallions for 50 x dollars
each, where x is the number of medallions produced each
week, then he can sell all that he makes. His fixed costs are
$350 per week. If he wants to sell all he makes and show a
profit each week, what are the possible numbers of medal-
lions he should make?
62. A retailer sells file cabinets for 80 x dollars each, where x
is the number of cabinets she receives from the supplier
each week. She pays $10 for each file cabinet and has fixed
costs of $600 per week. How many file cabinets should she
order from the supplier each week to guarantee that she
makes a profit?
In Exercises 63–66, you will need the formula for the height h
of an object above the ground at time t seconds:
h 16t
2
v
0
t h
0
;
this formula was explained on page 249.
SPECIAL TOPICS 4.6.A Absolute Value Inequalities 317
63. A toy rocket is fired straight up from ground level with an
initial velocity of 80 feet per second. During what time
interval will it be at least 64 feet above the ground?
64. A projectile is fired straight up from ground level with an
initial velocity of 72 feet per second. During what time
interval is it at least 37 feet above the ground?
65. A ball is dropped from the roof of a 120-foot-high building.
During what time period will it be strictly between
56 feet and 39 feet above the ground?
66. A ball is thrown straight up from a 40-foot-high tower with
an initial velocity of 56 feet per second.
(a) During what time interval is the ball at least 8 feet
above the ground?
(b) During what time interval is the ball between 53 feet
and 80 feet above the ground?
67. (a) Solve the inequalities x
2
x and x
2
x.
(b) Use the results of part (a) to show that for any nonzero
real number c with c 1, it is always true that
c
2
c.
(c) Use the results of part (a) to show that for any nonzero
real number c with c 1, it is always true that
c
2
c.
68. (a) If 0 a b, prove that 1/a 1/b.
(b) If a b 0, prove that 1/a 1/b.
(c) If a 0 b, how are 1/a and 1/b related?
THINKERS
In Exercises 69–77, solve the inequality.
69. 4x 5 4x 2 70. 3x 4 3x 4
71. 3x 4 3x 4 72. (x p)
2
0
73. (x 2)
2
(x 3)
2
0 74. (2x 5)
2
0
75. (x 1)
2
0 76. 3 6x 6 2
77. 8 4x 2 8
78. We know that for large values of x, we can approximate
x
2
2x
2
x 1 by using x
3
.
(a) Compute the percent error in this approximation when
x 50 and when x 100.
(b) For what positive values of x is the error less than 10%?
4.6.A SPECIAL TOPICS Absolute Value Inequalities
■ Solve absolute value inequalities algebraically and graphically.
Polynomial and rational inequalities involving absolute value can be solved graph-
ically, just as was done earlier: Rewrite the inequality in an equivalent form that
has 0 on the right side of the inequality sign; then graph the function whose rule is
given by the left side and determine where the graph is above or below the x-axis.
Section Objective
EXAMPLE 1
Solve
x
x
4
2
3
SOLUTION We use the equivalent inequality
x
x
4
2
3 0
and graph the function f (x)
x
x
4
2
3 (Figure 4–58). The graph is above the
x-axis between the two x-intercepts, which can be found algebraically or graphically.
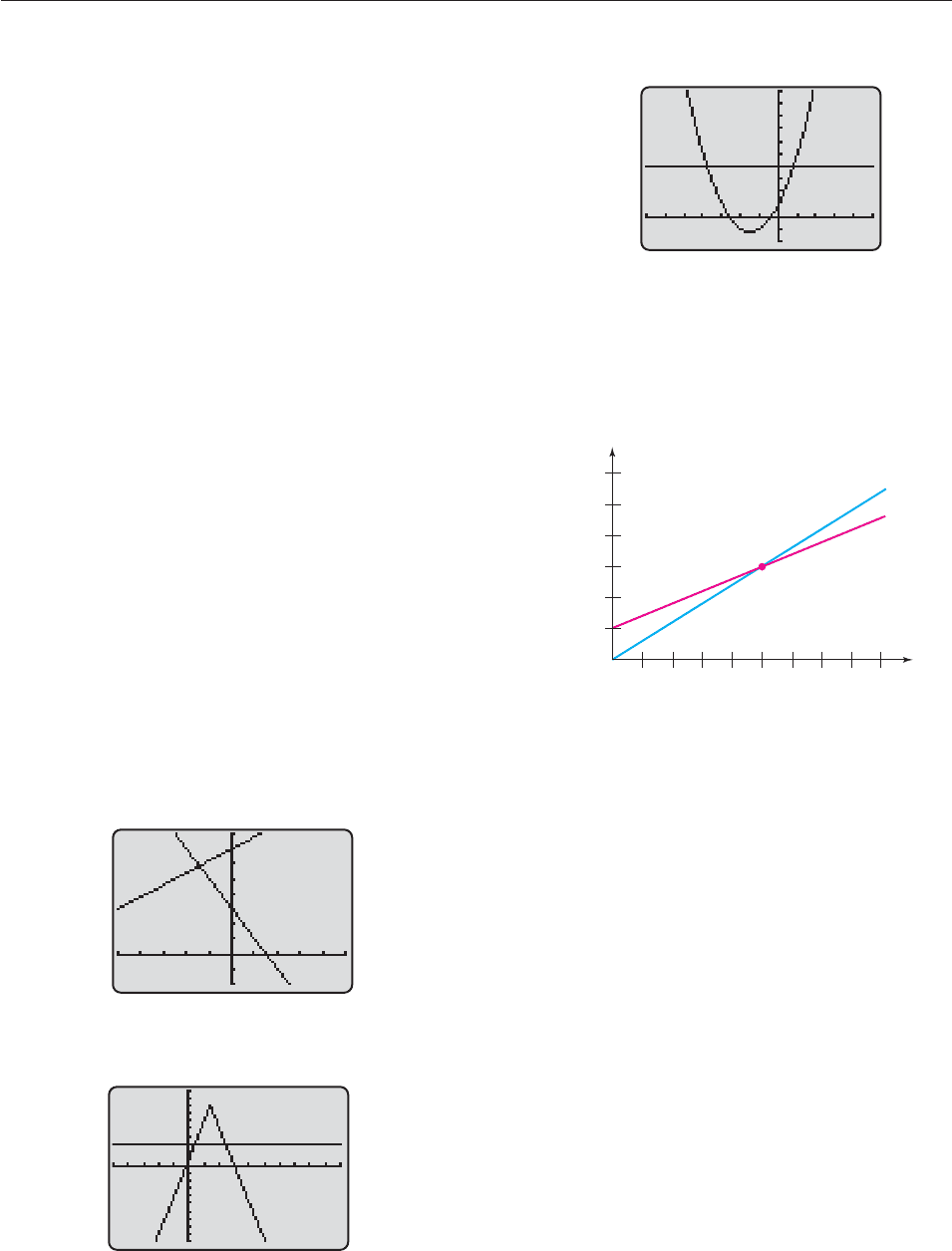
318 CHAPTER 4 Polynomial and Rational Functions
Verify that the x-intercepts are x 1/2 and x 5.
GRAPHING EXPLORATION
Since f (x) is not defined at x 2 (where the graph has a vertical asymptote),
the solutions of the original inequality are all x such that 1/2 x 2 or
2 x 5. ■
EXAMPLE 2
Solve x
4
2x
2
x 2 11x.
SOLUTION We determine the numbers for which the graph of
f (x) x
4
2x
2
x 2 11x
lies below the x-axis. (Why?) Convince yourself that the graph of f (x) in Fig-
ure 4–59 is complete.
8
6
−6
−8
Figure 4–59
10
9.6
−9.4
−10
Figure 4–58
A root finder shows that the approximate x-intercepts are x .17 and x 1.92.
Therefore, the approximate solutions of the original inequality (the numbers
where the graph is below the x-axis) are all x such that .17 x 1.92. ■
ALGEBRAIC METHODS
Most linear and quadratic inequalities involving absolute values can be solved
exactly by algebraic means. In fact, this is often the easiest way to solve such
inequalities. The key to the algebraic method is the fact that the absolute value of

a number can be interpreted as distance on the number line. For example, the
inequality r 5 states that the distance from r to 0 (namely, r ) is 5 units or less.
A glance at the number line in Figure 4–60 shows that these are the numbers r
with 5 r 5.
SPECIAL TOPICS 4.6.A Absolute Value Inequalities 319
−3 −2 −1−6 −5−8 −7 −4 0 1
5 units 5 units
2 3 4 5 6 7 8
Figure 4–60
Absolute Value
Inequalities
Let k be a positive number and r any real number.
r k is equivalent to k r k.
r k is equivalent to r k or r k.
EXAMPLE 3
To solve 3x 7 11, apply the first fact in the box, with 3x 7 in place of r and
11 in place of k, and obtain this equivalent inequality: 11 3x 7 11. Then
Add 7 to each part: 4 3x 18
Divide each part by 3: 4/3 x 6.
Therefore, the solutions of the original inequality are all numbers in the interval
[4/3, 6]. ■
EXAMPLE 4
To solve 5x 2 3, apply the second fact in the box, with 5x 2 in place of r,
and 3 in place of k, and in place of . This produces the equivalent statement:
5x 2 3or5x 2 3
5x 55x 1
x 1or x 1/5.
Therefore, the solutions of the original inequality are the numbers in either of the
intervals (, 1) or (1/5, ), as shown in Figure 4–61. ■
EXAMPLE 5
If a and d are real numbers with d positive, then the inequality x a d is
equivalent to d x a d. Adding a to each part shows that
a d x a d as shown in Figure 4–62. ■
1
1
5
Figure 4–61
a a a
Figure 4–62
Similarly, the numbers r such that r 5 are those whose distance to 0 is 5 or
more units, that is, the numbers r with r 5 or r 5. This argument works with
any positive number k in place of 5 and proves the following facts (which are also
true with and in place of and ).

EXAMPLE 6
To solve x
2
x 4 2, we use the fact in the box on the preceding page to re-
place it by an equivalent inequality:
x
2
x 4 2orx
2
x 4 2,
which is the same as
x
2
x 2 0orx
2
x 6 0.
The solutions are all numbers that are solutions of either one of the two inequalities.
To solve the first of these inequalities, note that the graph of
f (x) x
2
x 2 (x 1)(x 2)
is an upward-opening parabola that crosses the x-axis at 1 and 2 (the roots of
f (x)). Therefore, the solutions of
x
2
x 2 0
(the numbers for which the graph of f (x) is on or below the x-axis) are all x with
1 x 2. The second inequality above, x
2
x 6 0, is solved similarly.
320 CHAPTER 4 Polynomial and Rational Functions
What is the shape of the graph of g(x) x
2
x 6 and what are its x-intercepts?
GRAPHING EXPLORATION
This Graphing Exploration shows that the solutions of the second inequality (the
numbers for which the graph of g(x) is on or above the x-axis) are all x with
x 2 or x 3.
Consequently, the solutions of the original inequality are all numbers x such
that x 2 or 1 x 2 or x 3, as shown in Figure 4–63. ■
−2 −1 2
Solutions of x
2
− x − 2 < 0
3
Solutions of x
2
− x − 6 < 0
Solutions of either one
Figure 4–63
EXERCISES 4.6.A
In Exercises 1–30, solve the inequality. Find exact solutions
when possible and approximate ones otherwise.
1. 3x 2 2 2. 4x 2 8
3. 3 2x 2/3 4. 4 5x 4
5. 5x 2
3
4
6. 5 2x 7
7.
1
5
2
2x
1
4
8.
5
6
3x
7
6
9.
x
x
1
2
3 10.
3
x
x
1
5
2
11.
1
2
4
3
x
x
1 12.
3
1
x
2
1
x
2

■ Add, subtract and multiply complex numbers.
■ Use the conjugate of the denominator to express complex
fractions in standard form.
■ Express the square root of a negative number as an imaginary
number.
■ Find all solutions of a quadratic equation in the complex
number system.
Using mathematics to solve real-world problems is usually the same, regardless
of the application. A situation is modeled mathematically, then the model is
worked on using the tools of mathematics (algebra, trigonometry, calculus, dif-
ferential equations, etc.). Finally, some sort of real world prediction or answer is
taken from the result. In many applications (such as those dealing with electrical
impedance or sound waves with a fixed frequency), it is necessary to be able to
work with square roots in the model, even if negative numbers are involved.
Complex numbers were created to deal with this situation.
The first step in constructing the complex numbers is to define a number i
with the property that i
2
1 (or equivalently that i l
). Many people are
bothered when they see this definition, for no real number can produce a nega-
tive result when squared. The great mathematician Rene Descartes was one of
those people, and he derisively called i an “imaginary number,” a name which it
retains to this day even though, in many real contexts, i is just as important a
number as 5.
SECTION 4.7 Complex Numbers 321
13. x
2
2 1 14. x
2
4 3
15. x
2
2 4 16.
x
2
1
1
2
17. x
2
x 1 1 18. x
2
3x 4 6
19. x
5
x
3
1 2 20. 4x x
3
1
21. x
4
x
3
x
2
x 1 4
22. x
3
6x
2
4x 5 3
23.
x
x
2
3
4 24.
x
x
2
2
9
4
2
25.
x
2
3
x
2
x
2
2
x
x
12
2
2 26.
x
x
2
2
x
x
2
2
3
27. x
2
3x 2 0 28. x
2
3x 2 0
29. x
2
3x 2 0 30. x
2
3x 2 0
THINKERS
31. Let E be a fixed real number. Show that every solution of
x 3 E/5 is also a solution of (5x 4) 11 E.
32. Let a and b be fixed real numbers with a b. Show that the
solutions of
x
a
2
b
b
2
a
are all x with a x b.
33. A factory manufactures iron rods. The customer specifies
the length of the rod, and the factory produces the desired
item. Obviously, they aren’t going to be able to make
the length exact, but they guarantee that the manufactured
rod will be within 1 millimeter of the requested length.
(a) If a customer orders a rod of length 3 meters, what is
the range of acceptable lengths of rod for the factory to
produce?
(b) If a customer orders a rod of length d meters, what is
the acceptable range? Write your answer as a single
absolute value inequality, and label all variables you
use.
4.7 Complex Numbers
Section Objectives

The formal construction of the complex number system is rather involved,
and is presented in Exercise 81. For now, we simply summarize the results.
The real numbers are the complex numbers of the form a 0i, such as
7 7 0i. Following Descartes, complex numbers of the form 0 bi such as
5i and (1/4)i are called imaginary numbers. Since the usual laws of arith-
metic still hold, it’s easy to add, subtract, and multiply complex numbers. As
the following examples demonstrate, all symbols can be treated as if they were
real numbers, provided that i
2
is replaced by 1. Unless directed otherwise,
express your answers in the standard form a bi.
EXAMPLE 1
(a) (1 i) (3 7i) 1 i 3 7i
(1 3) (i 7i) 4 6i.
(b) (4 3i) (8 6i) 4 3i 8 (6i)
(4 8) (3i 6i) 4 9i.
(c) 4i
2
1
2
i
4i
2 4i
1
2
i
8i 4
1
2
i
2
8i 2i
2
8i 2(1)
2 8i.
(d) (2 i)(3 4i) 2
3 2(4i) i
3 i(4i)
6 8i 3i 4i
2
6 8i 3i 4(1)
(6 4) (8i 3i)
10 5i. ■
322 CHAPTER 4 Polynomial and Rational Functions
Properties of the Complex
Number System
1. The complex number system contains all real numbers.
2. The complex number system contains a number i such that i
2
1.
3. Addition, subtraction, multiplication, and division of complex numbers
obey the same rules of arithmetic that hold in the real number system,
with one exception: The exponent laws hold for integer exponents, but
not necessarily for fractional ones.
4. Every complex number can be written in the standard form a bi,
where a and b are real numbers.*
5. Two complex numbers a bi and c di are equal exactly when
a c and b d.
*Hereafter, whenever we write a bi or c di, it is assumed that a, b, c, d are real numbers and
i
2
1.
The familiar multiplication patterns and exponent laws for integer exponents
hold in the complex number system.
EXAMPLE 2
(a) (3 2i)(3 2i) 3
2
(2i)
2
9 4i
2
9 4(1)
9 4 13.
(b) (4 i)
2
4
2
2
4
i i
2
16 8i (1)
15 8i.
(c) To find i
54
, we first note that i
4
i
2
i
2
(1)(1) 1 and that
54 52 2 4
13 2.
Consequently,
i
54
i
522
i
52
i
2
i
4
13
i
2
(i
4
)
13
i
2
1
13
(1) 1. ■
The conjugate of the complex number a bi is the number a bi, and the
conjugate of a bi is a bi. For example, the conjugate of 3 4i is 3 4i and
the conjugate of 3i 0 3i is 0 3i 3i. Every real number is its own con-
jugate; for instance, the conjugate of 17 17 0i is 17 0i 17.
For any complex number a bi, we have
(a bi)(a bi) a
2
(bi)
2
a
2
b
2
i
2
a
2
b
2
(1) a
2
b
2
.
Since a
2
and b
2
are nonnegative real numbers, so is a
2
b
2
. Therefore, the prod-
uct of a complex number and its conjugate is a nonnegative real number. This fact
enables us to express quotients of complex numbers in standard form.
EXAMPLE 3
To express
3
1
4
2
i
i
in the form a bi, multiply both numerator and denominator
by the conjugate of the denominator, namely, 1 2i:
3
1
4
2
i
i
3
1
4
2
i
i
1
1
2
2
i
i
(
(
3
1
4
2
i
i
)
)
(
(
1
1
2
2
i
i
)
)
3
1
4
2
i
(
6
2
i
i)
2
8i
2
1
1
1
4
(
2i
1)
11
5
2i
1
5
1
2
5
i.
This is the form a bi with a 11/5 and b 2/5. ■
3 4i 6i 8(1)
1 4i
2
SECTION 4.7 Complex Numbers 323
TECHNOLOGY TIP
To do complex arithmetic on TI-86 and
HP-39gs, enter a bi as (a, b). On
other calculators, use the special i key
whose location is
TI-84+/89: keyboard
Casio: 9850: OPTN/CPLX

EXAMPLE 4
Express
1
1
i
in standard form.
SOLUTION We note that the conjugate of the denominator is 1 i, and
therefore
1
1
i
1
1
2
i
i
2
1
1
(
i
1)
1
2
i
1
2
1
2
i.
We can check this result by multiplying
1
2
1
2
i by 1 i to see whether the prod-
uct is 1
which it should be if
1
2
1
2
i
1
1
i
:
1
2
1
2
i
(1 i)
1
2
1
1
2
i
1
2
i
1
1
2
i
2
1
2
1
2
(1) 1. ■
Since i
2
1, we define 1
to be the complex number i. Similarly, since
(5i)
2
5
2
i
2
25(1) 25, we define 25
to be 5i. In general,
1
(1 i)
(1 i)(1 i)
324 CHAPTER 4 Polynomial and Rational Functions
Square Roots
of Negative Numbers
Let b be a positive real number.
b
is defined to be b
i
because (b
i)
2
(b
)
2
i
2
b(1) b.
EXAMPLE 5
Express the following in the form a bi:(a)3
(b)
1
3
7
SOLUTION
(a) 3
3
i 0 3
i or 0 i 3
.
(b)
1
3
7
1
3
7
i
1
3
3
7
i. ■
CAUTION
b
i is not the same as bi
. To avoid confusion it may help to write b
i as i b
.

EXAMPLE 6
(7 4
)(5 9
) (7 4
i)(5 9
i)
(7 2i)(5 3i)
35 21i 10i 6i
2
35 11i 6(1) 41 11i. ■
Since every negative real number has a square root in the complex number
system, we can now find complex solutions for equations that have no real
solutions. For example, the solutions of x
2
25 are x 25
5i.
In fact,
Every quadratic equation with real coefficients has solutions in
the complex number system.
EXAMPLE 7
To solve the equation 2x
2
x 3 0, we apply the quadratic formula.
x
1
4
23
.
Since 23
is not a real number, this equation has no real number solutions. But
23
is a complex number, namely, 23
23i. Thus, the equation does
have solutions in the complex number system.
x
1
4
23
1
4
23i
1
4
4
23
i.
Note that the two solutions,
1
4
4
23
i and
1
4
4
23
i, are conjugates of
each other. ■
1
1
2
4
2
3
2
2
SECTION 4.7 Complex Numbers 325
CAUTION
The property cd
c
d
(or equivalently in exponential notation, (cd )
1/2
c
1/2
d
1/2
),
which is valid for positive real numbers, does not hold when both c and d are negative.
20
5
20
i
5
i 20
5
i
2
20
5
(1)
100
(1) 10.
But (20)(
5)
100
10, so that
(20)(
5)
20
5
.
To avoid difficulty, always write square roots of negative numbers in terms of i before doing any
simplification.
TECHNOLOGY TIP
Most calculators that do complex
number arithmetic automatically return
a complex number when asked for the
square root of a negative number. On
TI-84+/89, however, the MODE must
be set to “rectangular” or “a bi.”
