Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

EXAMPLE 3
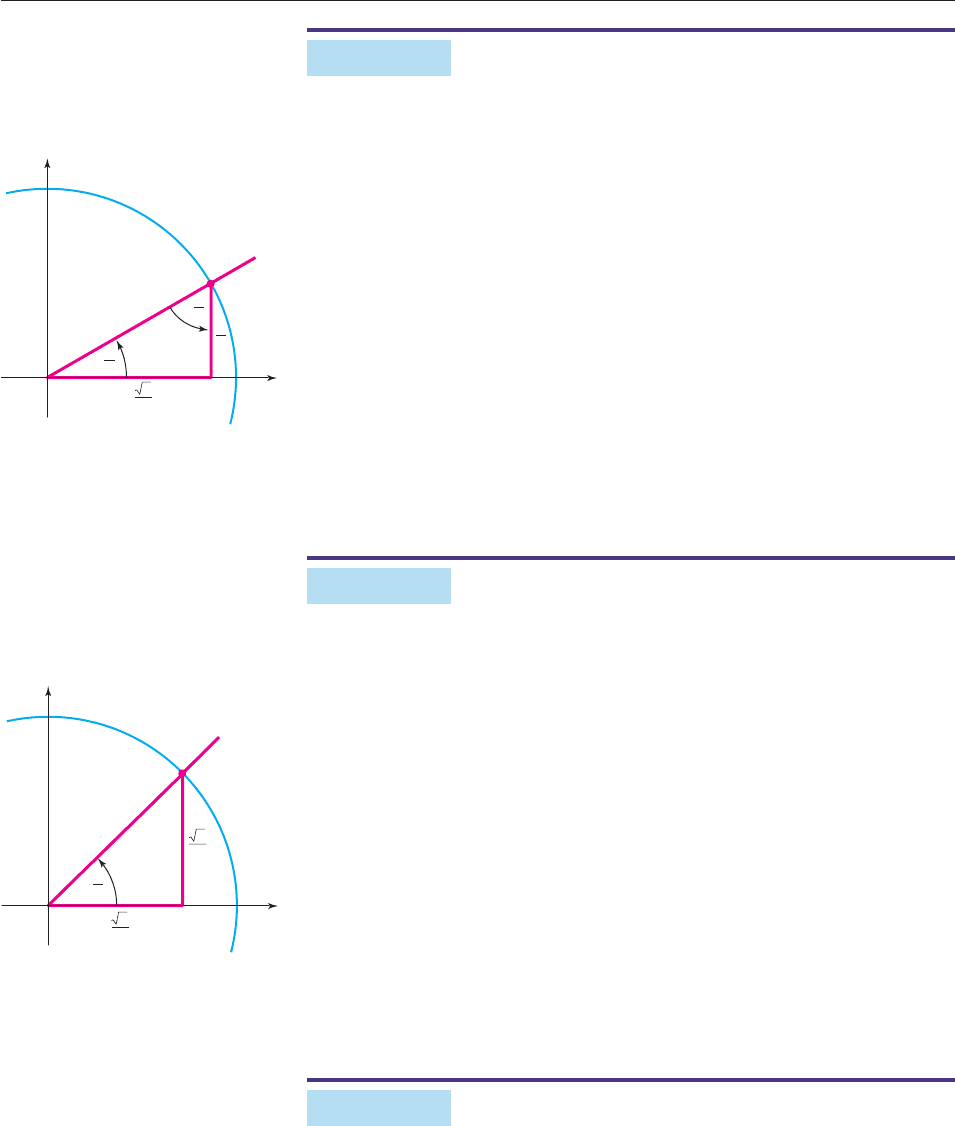
Evaluate the three trigonometric functions at t p6.
SOLUTION Construct an angle of p6 radians in standard position and let P
be the point where its terminal side intersects the unit circle. Draw a vertical line
from P to the x-axis, as shown in Figure 6–21, forming a right triangle that
matches the first triangle in Figure 6–20. The sides of this triangle show that P has
coordinates (
3
2, 12). By the definition,
sin
p
6
y-coordinate of P
1
2
cos
p
6
x-coordinate of P
2
3
tan
p
6
c
s
o
in
s
(
(
p
p
/
/
6
6
)
)
1/
3
/
2
2
1
3
3
3
. ■
EXAMPLE 4
Evaluate the trigonometric functions at t p4.
SOLUTION Construct an angle of p4 radians in standard position whose
terminal side intersects the unit circle at P. Draw a vertical line from P to the
x-axis to form a right triangle that matches the second triangle in Figure 6–20. As
Figure 6–22 shows, P has coordinates (2
2, 2
2) so that
sin
p
4
y-coordinate of P
2
2
cos
p
4
x-coordinate of P
2
2
tan
p
4
c
s
o
in
s
(
(
p
p
/
/
6
6
)
)
2
2
2
2
1. ■
EXAMPLE 5
Evaluate the trigonometric functions at 5p/4.
SOLUTION Construct an angle of 5p/4 radians in standard position and let P
be the point where the terminal side intersects the unit circle. Draw a vertical line
from P to the x-axis, as shown in Figure 6–23, forming a right triangle that matches
446 CHAPTER 6 Trigonometric Functions
1
2
3
1
1
2
π
3
π
6
1
x
P
y
Figure 6–21
2
1
1
2
π
4
2
2
1
x
P
y
Figure 6–22
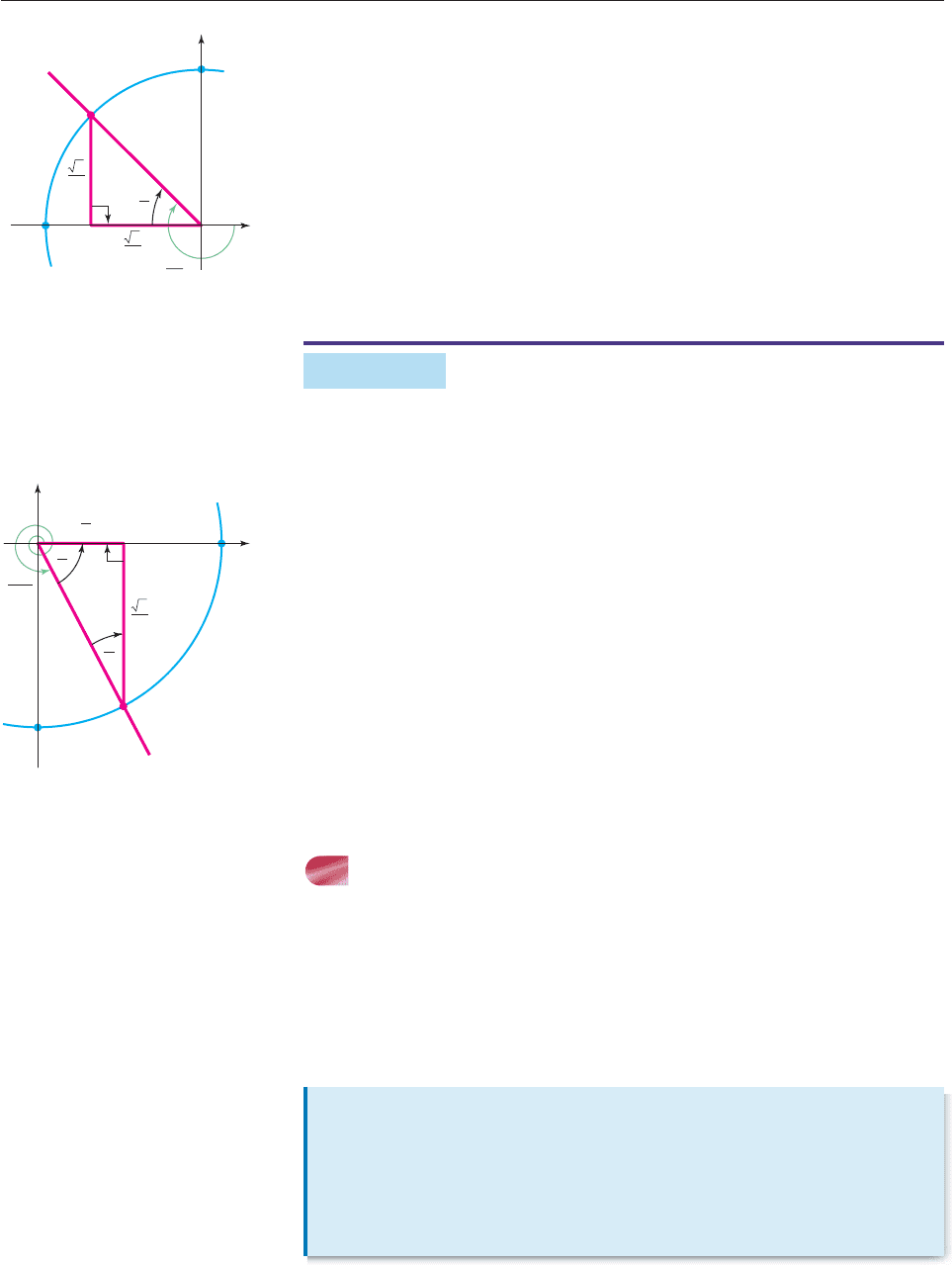
the second triangle in Figure 6–20. The sides of the triangle in Figure 6–23 show
that P has coordinates (2
/2, 2
/2). Hence,
sin
4
5p
y-coordinate of P
2
2
cos
4
5p
x-coordinate of P
2
2
tan
4
5p
c
s
o
in
s
t
t
2
2
/
/
2
2
1. ■
EXAMPLE 6
Evaluate the trigonometric functions at 11p/3.
SOLUTION Construct an angle of 11p/3 radians in standard position and
draw a vertical line from the x-axis to the point P where the terminal side of the
angle meets the unit circle, as shown in Figure 6–24. The right triangle formed in
this way matches the first triangle in Figure 6–20. The sides of the triangle in
Figure 6–24 show that the coordinates of P are (1/2, 3
/2). Therefore,
sin
11
3
p
y-coordinate of P
2
3
cos
11
3
p
x-coordinate of P
1
2
tan
11
3
p
(
(
c
s
o
in
s
1
1
1
1
p
p
/
/
3
3
)
)
1/
3
2
/2
3
. ■
POINT-IN-THE-PLANE DESCRIPTION
OF TRIGONOMETRIC FUNCTIONS
In evaluating sin t, cos t and tan t, from the definition, we use the point where the
unit circle intersects the terminal side of an angle of t radians in standard position.
Here is an alternative method of evaluating the trigonometric functions that uses
any point on the terminal side of the angle (except the origin); it is proved at the
end of this section.
SECTION 6.2 The Sine, Cosine, and Tangent Functions 447
2
1
⫺1
⫺
2
π
4
2
2
5π
4
1
x
P
y
Figure 6–23
Point-in-the-Plane
Description
Let t be a real number. Let (x, y) be any point (except the origin) on the
terminal side of an angle of t radians in standard position. Then,
sin t
y
r
cos t
x
r
tan t
y
x
where r
x
2
y
2
is the distance from (x, y) to the origin.
3
1
2
π
6
π
3
1
2
11π
3
1
−1
x
P
y
Figure 6–24

EXAMPLE 7
Figure 6–25 shows an angle of t radians in standard position. Evaluate the three
trigonometric functions at t.
SOLUTION Apply the facts in the box above with (x, y) (3, 4) and
r
x
2
y
2
3
2
(
4)
2
25 5.
Then we have
sin t
y
r
5
4
4
5
, cos t
x
r
3
5
, tan t
y
x
3
4
4
3
. ■
EXAMPLE 8
The terminal side of a first-quadrant angle of t radians in standard position lies on
the line with equation 2x 3y 0. Evaluate the three trigonometric functions at t.
SOLUTION Verify that the point (3, 2) satisfies the equation and hence lies on
the terminal side of the angle (Figure 6–26). Now we have
(x, y) (3, 2) and r
x
2
y
2
3
2
2
2
13.
Therefore,
sin t
y
r
2
13
, cos t
x
r
3
13
, tan t
y
x
2
3
/
/
1
1
3
3
2
3
. ■
Proof of the Point-in-the-Plane Description Let Q be the point on the ter-
minal side of the standard position angle of t radians and let P be the point where
the terminal side meets the unit circle, as in Figure 6–27. The definition of sine
and cosine shows that P has coordinates (cos t, sin t). The distance formula shows
that the segment OQ has length
x
2
y
2
, which we denote by r.
Figure 6–27
1
sin t
cos t
1
(x, y)
(cos t, sin t)
y
x
x
P
O
SR
Q
t
y
448 CHAPTER 6 Trigonometric Functions
(3, −4)
x
t
y
Figure 6–25
(3, 2)
1
1
x
t
y
Figure 6–26
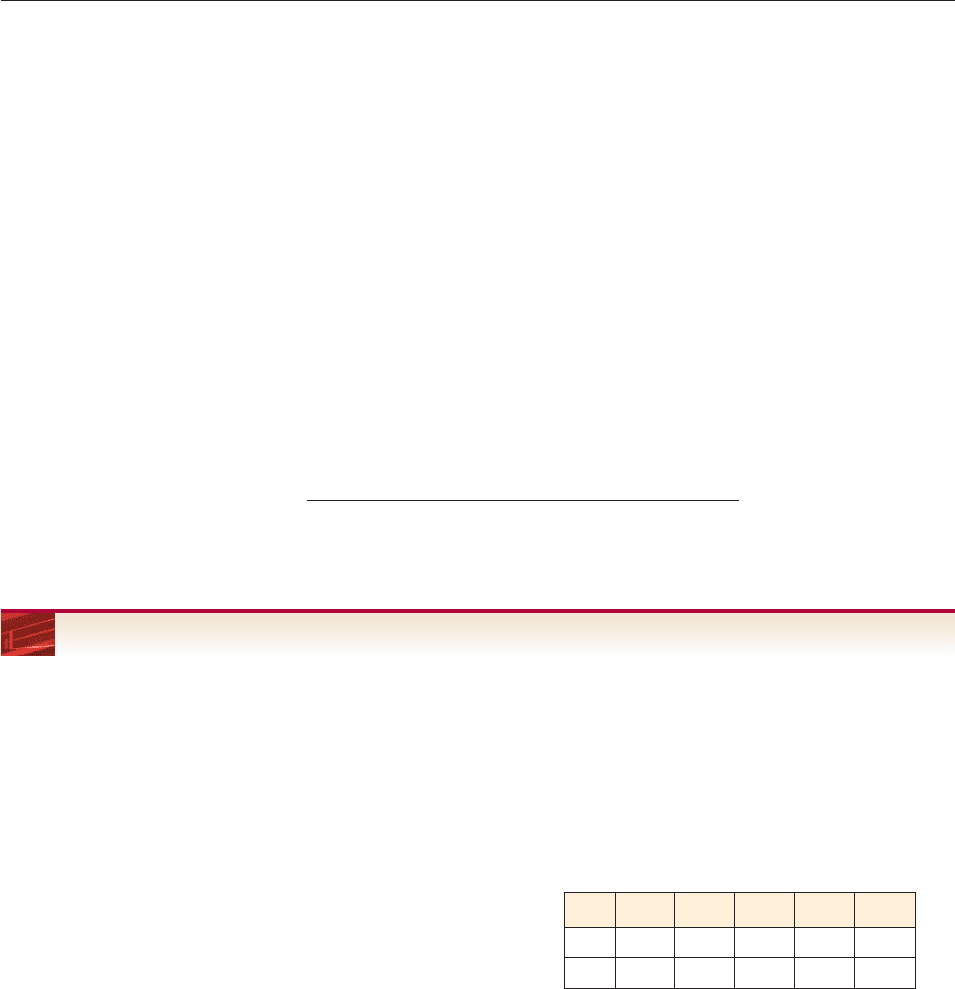
Both triangles QOR and POS are right triangles containing an angle of t radi-
ans. Therefore, these triangles are similar.* Consequently,
l
l
e
e
n
n
g
g
t
t
h
h
O
O
Q
P
l
l
e
e
n
n
g
g
t
t
h
h
Q
PS
R
and
l
l
e
e
n
n
g
g
t
t
h
h
O
O
Q
P
l
l
e
e
n
n
g
g
t
t
h
h
O
O
R
S
.
Figure 6–23 shows what each of these lengths is. Hence,
1
r
si
y
n t
and
1
r
co
x
s t
r sin t yrcos t x
sin t
y
r
cos t
x
r
Similar arguments work when the terminal side is not in the first quadrant.
In every case, tan t
c
s
o
in
s
t
t
y
x
/
/
r
r
y
x
. This completes the proof of the state-
ments in the box on page 447. ■
SECTION 6.2 The Sine, Cosine, and Tangent Functions 449
*See the Geometry Review Appendix for the basic facts about similar triangles.
EXERCISES 6.2
Note: Unless stated otherwise, all angles are in standard
position.
In Exercises 1–10, use the definition (not a calculator) to find
the function value.
1. sin(3p/2) 2. sin(p) 3. cos(3p/2)
4. cos(p/2) 5. tan(4p) 6. tan(p)
7. cos(3p/2) 8. sin(9p/2) 9. cos(11p/2)
10. tan(13p)
In Exercises 11–14, assume that the terminal side of an angle
of t radians passes through the given point on the unit circle.
Find sin t, cos t, tan t.
11. (2/5
, 1/5
) 12. (1/10, 3/10)
13. (3/5, 4/5) 14. (.6, .8)
In Exercises 15–29, find the exact value of the sine, cosine, and
tangent of the number, without using a calculator.
15. p/3 16. 2p/3 17. 7p/4
18. 5p/4 19. 3p/4 20. 7p/3
21. 5p/6 22. 3p 23. 23p/6
24. 11p/6 25. 19p/3 26. 10p/3
27. 15p/4 28. 25p/4 29. 17p/2
30. Fill the blanks in the following table. Write each entry as a
fraction with denominator 2 and with a radical in the
numerator. For example,
sin
p
2
1
2
4
.
Some students find the resulting pattern an easy way to
remember these functional values.
In Exercises 31–36, write the expression as a single real num-
ber. Do not use decimal approximations. [Hint: Exercises
15–21 may be helpful.]
31. sin(p/3) cos(p) sin(p) cos(p/3)
32. sin(p/6) cos(p/2) cos(p/6) sin(p/2)
33. cos(p/2) cos(p/4) sin(p/2) sin(p/4)
34. cos(2p/3) cos(p) sin(2p/3) sin(p)
35. sin(3p/4) cos(5p/6) cos(3p/4) sin(5p/6)
36. sin(7p/3) cos(5p/4) cos(7p/3) sin(5p/4)
t 0 p/6 p/4 p/3 p/2
sin t
cos t
450 CHAPTER 6 Trigonometric Functions
In Exercises 37–42, find sin t, cos t, tan t when the terminal
side of an angle of t radians in standard position passes
through the given point.
37. (3, 5) 38. (2, 1)
39. (4, 5) 40. (3, 4)
41. (3
, 8) 42. (2, p)
In Exercises 43–46, use a calculator in radian mode.
43. When a plane flies faster than the speed of sound, the sound
waves it generates trail the plane in a cone shape, as shown
in the figure. When the bottom part of the cone hits the
ground, you hear a sonic boom. The equation that describes
this situation is
sin
2
t
w
p
,
where t is the radian measure of the angle of the cone, w
is the speed of the sound wave, p is the speed of the plane,
and p w.
(a) Find the speed of the sound wave when the plane flies
at 1200 mph and t .8.
(b) Find the speed of the plane if the sound wave travels at
500 mph and t .7.
44. Suppose the batter in Example 2 hits the ball with an initial
velocity of 100 feet per second.
(a) Complete this table.
(b) By experimentation, find the value of t (to two decimal
places) that produces the longest distance.
(c) If t 1.6, what is d? Explain your answer.
45. The average daily temperature in St. Louis, Missouri (in
degrees Fahrenheit), is approximated by the function
T(x) 24.6 sin(.522x 2.1) 56.3 (1 x 13),
where x 1 corresponds to January 1, x 2 to February 1,
etc.*
t
(a) Complete this table.
(b) Make a table that shows the average temperature every
third day in June, beginning on June 1. [Assume that
three days 1/10 of a month.]
46. A regular polygon has n equal sides and n equal angles
formed by the sides. For example, a regular polygon of three
sides is an equilateral triangle, and a regular polygon of
four sides is a square. If a regular polygon of n sides is cir-
cumscribed around a circle of radius r, as shown in the figure
for n 4 and n 5, then the area of the polygon is given by
A nr
2
tan
p
n
.
(a) Find the area of a regular polygon of 12 sides circum-
scribed around a circle of radius 5.
(b) Complete the following table for a regular polygon of
n sides circumscribed around the unit circle (which, as
you recall, has radius 1).
(c) As n gets larger and larger, what number does the area
get very close to? [Hint: What is the area of the unit
circle?]
In Exercises 47–54, find the average rate of change of the func-
tion over the given interval. Exact answers are required.
47. f(t) cos t from t p2 to t p
48. g(t) sin t from t p2 to t p
49. g(t) sin t from t p6 to t 11p3
50. h(t) tan t from t p6 to t 11p3
51. f(t) cos t from t 5p4 to t p4
n 4 n 5
r
r
Average
Date Temperature
Jan. 1
Mar. 1
May 1
July 1
Sept. 1
Nov. 1
t .5 .6 .7 .8 .9
d
n 5 50 500 5000 10,000
Area
*Based on data from the National Climatic Data Center.
SECTION 6.2 The Sine, Cosine, and Tangent Functions 451
52. g(t) sin t from t 5p4 to t p4
53. h(t) tan t from t p6 to t p3
54. f(t) cos t from t p4 to t p3
55. (a) Use a calculator to find the average rate of change of
g(t) sin t from 2 to 2 h, for each of these values
of h: .01, .001, .0001, and .00001.
(b) Compare your answers in part (a) with the number
cos 2. What would you guess that the instantaneous rate
of change of g(t) sin t is at t 2?
56. (a) Use a calculator to find the average rate of change of
f(t) cos t from 5 to 5 h, for each of these values of
h: .01, .001, .0001, and .00001.
(b) Compare your answers in part (a) with the number
sin 5. What would you guess that the instantaneous
rate of change of f (t) cos t is at t 5?
In Exercises 57–62, assume that the terminal side of an angle
of t radians in standard position lies in the given quadrant on
the given straight line. Find sin t, cos t, tan t. [Hint: Find a
point on the terminal side of the angle.]
57. Quadrant IV; line with equation y 2x.
58. Quadrant III; line with equation 2y 5x 0.
59. Quadrant IV; line through (3, 5) and (9, 15).
60. Quadrant III; line through the origin parallel to
7x 2y 6.
61. Quadrant II; line through the origin parallel to
2y x 6.
62. Quadrant I; line through the origin perpendicular to
3y x 6.
63. The values of sin t, cos t, and tan t are determined by the point
(x, y) where the terminal side of an angle of t radians in stan-
dard position intersects the unit circle. The coordinates x and
y are positive or negative, depending on what quadrant (x, y)
lies in. For instance, in the second quadrant x is negative and
y is positive, so that cos t (which is x by definition) is negative.
Fill the blanks in this chart with the appropriate sign ( or ).
64. (a) Find two numbers c and d such that
sin(c d) sin c sin d.
(b) Find two numbers c and d such that
cos(c d) cos c cos d.
In Exercises 65–70, draw a rough sketch to determine if the
given number is positive.
65. sin 1 [Hint: The terminal side of an angle of 1 radian lies in
the first quadrant (why?), so any point on it will have a pos-
itive y-coordinate.]
66. cos 2 67. tan 3 68. (cos 2)(sin 2)
69. tan 1.5 70. cos 3 sin 3
In Exercises 71–76, find all the solutions of the equation.
71. sin t 1 72. cos t 1 73. tan t 0
74. sin t 1 75. sin t 1 76. cos t 1
THINKERS
77. Using only the definition and no calculator, determine
which number is larger: sin(cos 0) or cos(sin 0).
78. With your calculator in radian mode and function graphing
mode, graph the following functions on the same screen,
using the viewing window with 0 x 2p and 3 y
3: f (x) cos x
3
and g(x) (cos x)
3
. Are the graphs the
same? What do you conclude about the statement cos x
3
(cos x)
3
?
79. Figure R is a diagram of a merry-go-round that includes
horses A through F. The distance from the center P to A is
1 unit and the distance from P to D is 5 units. Define six
functions as follows:
A(t) vertical distance from horse A to the x-axis at
time t minutes;
Figure R
and similarly for B(t), C(t), D(t), E(t), F(t). The merry-
go-round rotates counterclockwise at a rate of 1 revolution
per minute, and the horses are in the positions shown in
Figure R at the starting time t 0. As the merry-go-round
rotates, the horses move around the circles shown in Figure R.
x
F
C
P
π
3
AD
B
E
y
π
4
Quadrant II
p /2 b t b p
Quadrant I
0 b t b p /2
sin t
cos t
tan t
sin t
cos t
tan t
Quadrant III
p b t b 3p /2
Quadrant IV
3p /2 b t b 2p
sin t
cos t
tan t
sin t
cos t
tan t
x
y

452 CHAPTER 6 Trigonometric Functions
(a) Show that B(t) A(t 1/8) for every t.
(b) In a similar manner, express C(t) in terms of the func-
tion A(t).
(c) Express E(t) and F(t) in terms of the function D(t).
(d) Explain why Figure S is valid and use it and similar
triangles to express D(t) in terms of A(t).
(e) In a similar manner, express E(t) and F(t) in terms of
A(t).
(f) Show that A(t) sin(2pt) for every t. [Hint:
Exercises 57–64 in Section 6.1 may be helpful.]
(g) Use parts (a), (b), and (f) to express B(t) and C(t) in
terms of the sine function.
(h) Use parts (d), (e), and (f) to express D(t), E(t), and F(t)
in terms of the sine function.
Figure S
P
x
5
1
A
A(t)
D(t)
D
6.2 ALTERNATE The Sine, Cosine, and Tangent Functions
■ Use the point-in-the-plane description to evaluate trigonometric
functions of real numbers.
■ Use the unit circle to define the sine, cosine and tangent
functions.
■ Find the exact values of sine, cosine, and tangent a p/3, p/4,
p/6, and integer multiples of these numbers.
Trigonometric functions of any angle are defined in Alternate Section 8.1, using a
point on the terminal side of the angle. According to that definition, the domains
of the sine, cosine, and tangent functions consist of angles. We now define
trigonometric functions whose domains consist of real numbers. The basic idea is
quite simple: If t is a real number, then
sin t is defined to be the sine of an angle of t radians.
cos t is defined to be the cosine of an angle of t radians.
tan t is defined to be the tangent of an angle of t radians.
In other words, instead of starting with an angle as in Chapter 8, we now start with
a number t and then move to an angle of t radians, as summarized here:
Trigonometric Functions of Real Numbers
64444444444444744444444444448
—— ——
144444442444444443
Trigonometric Functions of Angles
Adapting the definition of Alternate Section 8.1 to this new viewpoint, we have
the following.
Determine sin t,
cos t, tan t
Form an angle
of t radians
Begin with a
number t
NOTE
If you have not read Chapter 8, omit
this section. If you have read Chapter 8,
use this section in place of Section 6.2.
Section Objectives
Instructors who wish to cover all
six trigonometric functions
simultaneously should
incorporate Section 6.6 into
Sections 6.2–6.4, as follows.
Roadmap
Cover
Subsection of at the
Section 6.6 end of
Part I Section 6.2
Part II Section 6.3
Part III Section 6.4
EXAMPLE 1
Figure 6–28 shows an angle of t radians in standard position. Find sin t, cos t, and
tan t.
SOLUTION Apply the facts in the box above with (x, y) (3, 4) and
r
x
2
y
2
3
2
(
4)
2
25 5.
Then we have
sin t
y
r
5
4
4
5
. cos t
x
r
3
5
, tan t
y
x
3
4
4
3
. ■
EXAMPLE 2
The terminal side of a first-quadrant angle of t radians in standard position lies on
the line with equation 2x 3y 0. Evaluate the three trigonometric functions at t.
SOLUTION Verify that the point (3, 2) satisfies the equation and hence lies on
the terminal side of the angle (Figure 6–29). Now we have (x, y) (3, 2) and
r
x
2
y
2
3
2
2
2
13. Therefore,
sin t
y
r
2
13
, cos t
x
r
3
13
, tan t
y
x
2
3
/
/
1
1
3
3
2
3
. ■
For a few numbers, we can use our knowledge of special angles to evaluate the
trigonometric functions exactly.
EXAMPLE 3
Find the exact value of each of the following.
(a) sin
p
6
and cos
p
6
(b) sin
p
4
and cos
p
4
(c) tan
3
4
p
SOLUTION
(a) An angle of p6 radians is the same as an angle of 30. From Example 4(a)
of Section 8.1 we know the values of sine and cosine at 30:
sin
p
6
sin 30
1
2
and cos
p
6
cos 30
2
3
.
ALTERNATE 6.2 The Sine, Cosine, and Tangent Functions 453
Point-in-the-Plane
Description
Let t be a real number. Let (x, y) be any point (except the origin) on the ter-
minal side of an angle of t radians in standard position. Then
sin t
y
r
, cos t
x
r
, tan t
y
x
,
where r
x
2
y
2
is the distance from (x, y) to the origin.
(3, −4)
x
y
t
Figure 6–28
(3, 2)
1
1
x
t
y
Figure 6–29
(b) An angle of p4 radians is the same as an angle of 45. By Example 5 of
Section 8.1,
sin
p
4
sin 45
2
2
and cos
p
4
cos 45
2
2
.
(c) An angle of 3p4 radians is the same as an angle of 135, so from Example 12
of Alternate Section 8.1, we now have
tan
3
4
p
tan 1351. ■
In most cases, evaluating trigonometric functions is not as simple as it was in
the preceding examples. Usually, you must use a calculator (in radian mode) to
approximate the values of these functions, as illustrated in Figure 6–30.
EXAMPLE 4
When a baseball is hit by a bat, the horizontal distance d traveled by the ball is
approximated by
d
v
2
sin
16
t cos t
,
where the ball leaves the bat at an angle of t radians and has initial velocity v feet
per second, as shown in Figure 6–31.
(a) How far does the ball travel when the initial velocity is 90 feet per second and
t .7?
(b) If the initial velocity is 105 feet per second and t 1, how far does the ball
travel?
SOLUTION
(a) Let v 90 and t .7 in the formula for d. Then a calculator (in radian mode)
shows that
d
v
2
sin
16
t cos t
90
2
sin
1
.
6
7 cos .7
249.44 feet.
(b) Now let v 105 and t 1. Then
d
v
2
sin
16
t cos t
105
2
si
1
n
6
1 cos 1
313.28. ■
THE UNIT CIRCLE DESCRIPTION
We now develop a description of sine, cosine, and tangent that is based on the unit
circle, which is the circle of radius 1 with center at the origin, whose equation is
x
2
y
2
1. Let t be any real number and construct an angle of t radians in stan-
dard position. Let P (x, y) be the point where the terminal side of this angle
intersects the unit circle, as shown in Figure 6–32.
The distance from (x, y) to the origin is 1 unit because the radius of the unit
circle is 1. Using the point (x, y) and r 1, we see that
cos t
x
r
1
x
x and sin t
y
r
1
y
y.
In other words,
454 CHAPTER 6 Trigonometric Functions
TECHNOLOGY TIP
Throughout this chapter, be sure your
calculator is set for RADIAN mode. Use
the MODE(S) menu on TI and HP and
the SETUP menu Casio.
Figure 6–30
d
t
Figure 6–31
(x, y)
−1
−1
1
1
1
x
y
P
t
Figure 6–32
This description is often used as a definition of sine and cosine. To get a better
feel for it, do the following Graphing Exploration.
ALTERNATE 6.2 The Sine, Cosine, and Tangent Functions 455
Sine and
Cosine
If P is the point where the terminal side of an angle of t radians in standard
position meets the unit circle, then
P has coordinates (cos t, sin t).
GRAPHING EXPLORATION
With your calculator in radian mode and parametric graphing mode, set the range
values as follows:
0 t 2p, 1.8 x 1.8, 1.2 y 1.2*
Then graph the curve given by the parametric equations.
x cos t and y sin t.
The graph is the unit circle. Use the trace to move around the circle. At each point, the
screen will display three numbers: the values of t, x, and y. For each t, the cursor is on
the point where the terminal side of an angle of t radians meets the unit circle, so the
corresponding x is the number cos t and the corresponding y is the number sin t.
Suppose an angle of t radians in standard position intersects the unit circle at
the point (x, y), as in Figure 6–32. From our earlier definition, tan t y/x and by
the unit circle description, we have x cos t and y sin t. Therefore, we have
another description of the tangent function:
tan t
c
s
o
in
s
t
t
.
EXAMPLE 5
Use the unit circle description and the preceding equation to find the exact values
of sin t, cos t, and tan t when
(a) t p (b) t p/2.
SOLUTION
(a) Construct an angle of p radians, as in Figure 6–33. Its terminal side lies on
the negative x-axis and intersects the unit circle at P (1, 0). Hence,
sin p y-coordinate of P 0
cos p x-coordinate of P 1
tan p
c
s
o
in
s
p
p
0
1
0.
(x, y)
−1
−1
1
1
1
x
y
P
t
Figure 6–33
*Parametric graphing is explained in Special Topics 3.3.A. These settings give a square viewing
window on calculators with a screen measuring approximately 95 by 63 pixels (such as TI-84), and
hence the unit circle will look like a circle. For wider screens, adjust the x range settings to obtain a
square window.
