Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

RIGHT TRIANGLE DESCRIPTION
OF TRIGONOMETRIC FUNCTIONS
For angles between 0° and 90°, the trigonometric functions may be evaluated by
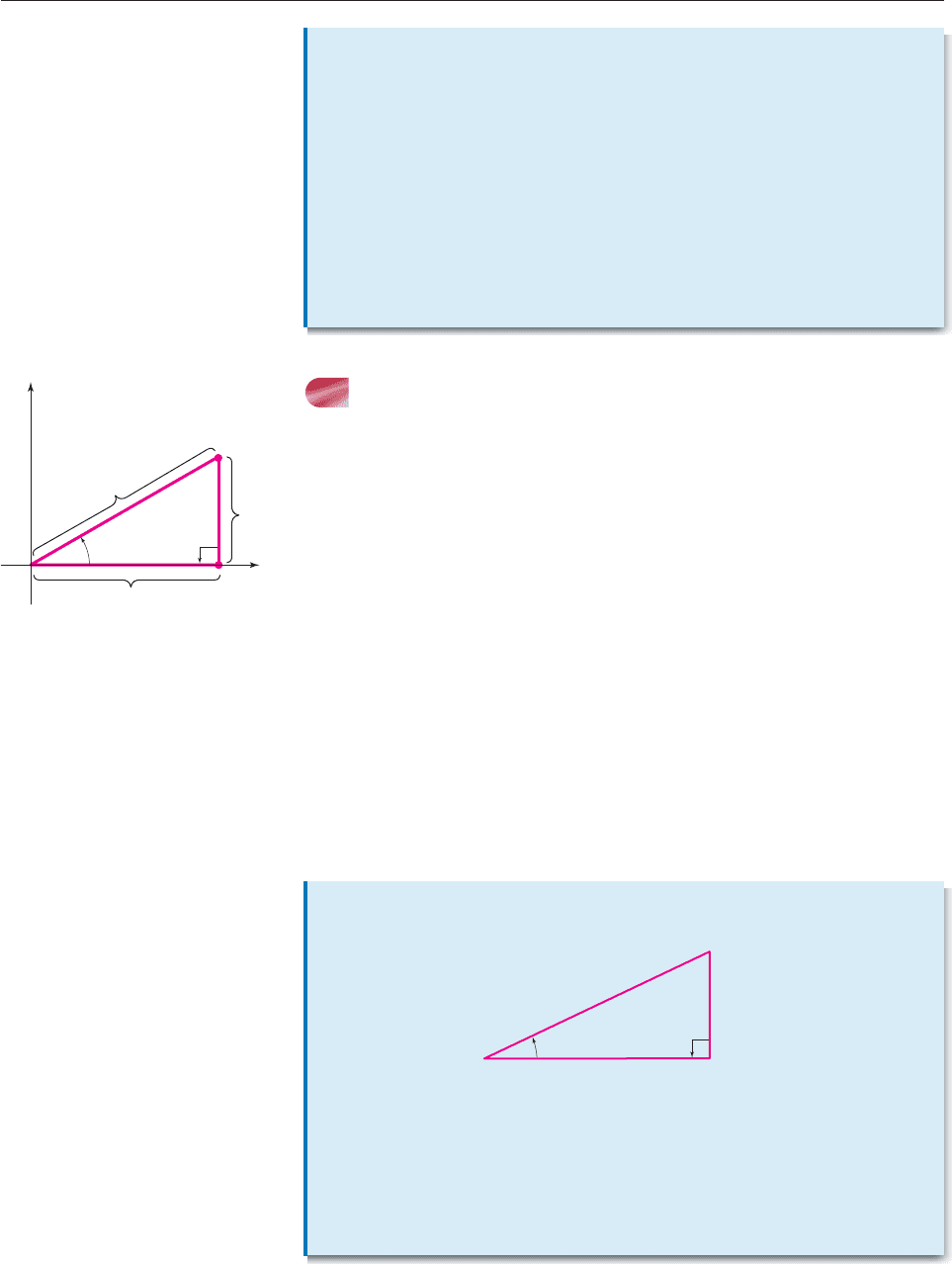
using right triangles as follows. Suppose u is an angle in a right triangle. Place the
triangle so that angle u is in standard position, with the hypotenuse as its terminal
side, as shown in Figure 8–2.
Denote the length of the side AB (the one adjacent to angle u) by u and the
length of side BC (the one opposite angle u) by v. Then the coordinates of C are
(u, v). Let r be the length of the hypotenuse AC (the distance from (u, v) to the ori-
gin). Then the point-in-the-plane description shows that
sin u
v
r
, cos u
u
r
,
tan u
u
v
,
and similarly for the other trigonometric functions. These facts can be summa-
rized as follows.
length of opposite side
length of adjacent side
length of adjacent side
length of hypotenuse
length of opposite side
length of hypotenuse
576 CHAPTER 8 Triangle Trigonometry
Identities for
Angles Measured
in Degrees
Periodicity Identities
sin(u 360°) sin u csc(u 360°) csc u
cos(u 360°) cos u sec(u 360°) sec u
tan(u 180°) tan u cot(u 180°) cot u
Pythagorean Identities
sin
2
u cos
2
u 11 tan
2
u sec
2
u 1 cot
2
u csc
2
u
Negative Angle Identities
sin(u) sin u cos(u) cos u tan(u) tan u
(u, v)
v
u
x
r
A
B
C
y
θ
Figure 8–2
Right Triangle
Description
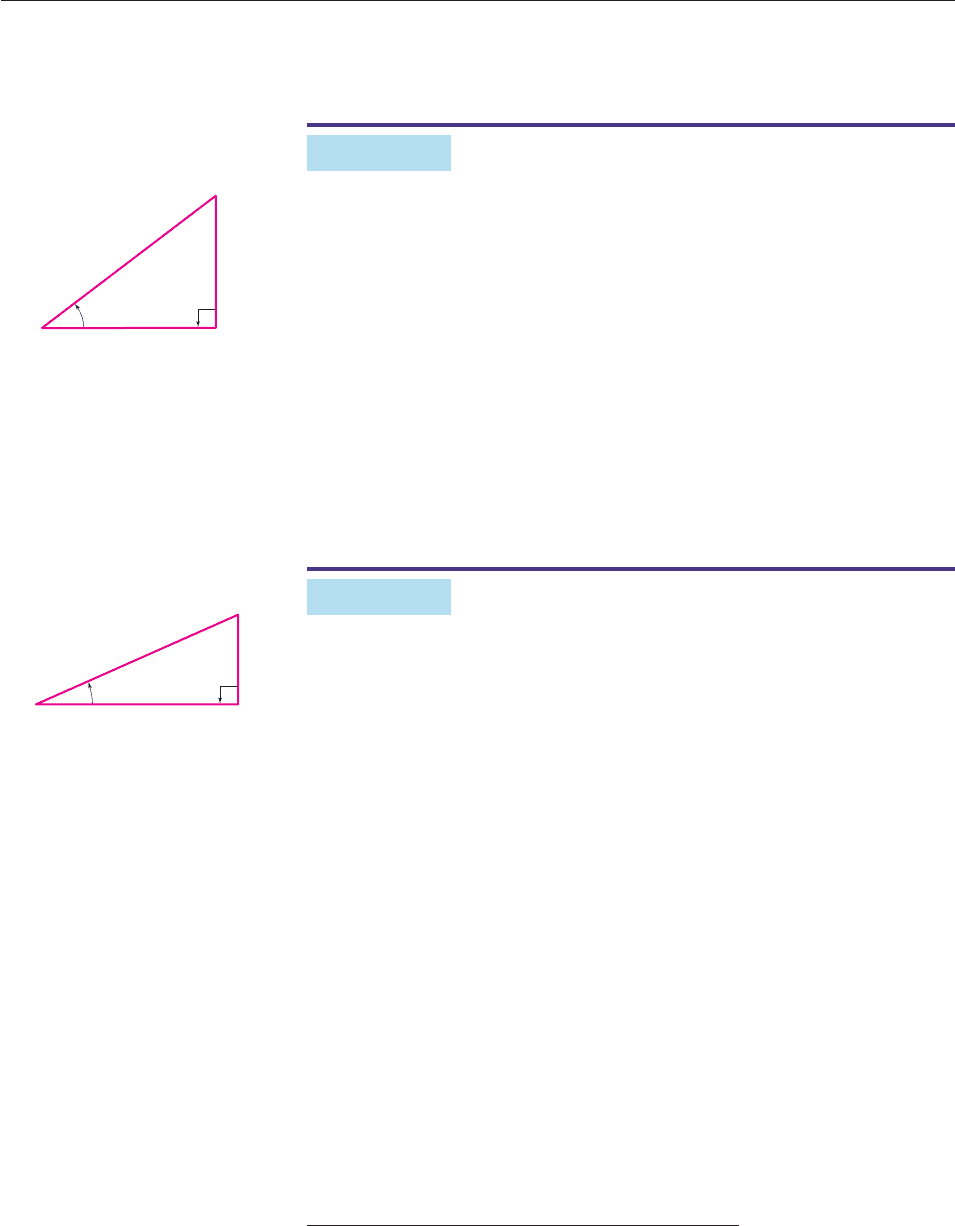
Consider a right triangle containing an angle u.
The values of the six trigonometric functions of the angle u are given by
sin u
hy
o
p
p
o
p
t
o
e
s
n
i
u
te
se
cos u
hy
a
p
d
o
ja
t
c
e
e
n
n
u
t
se
tan u
o
ad
p
j
p
a
o
c
s
e
i
n
te
t
csc u
hy
o
p
p
o
p
t
o
e
s
n
i
u
te
se
sec u
hy
a
p
d
o
ja
t
c
e
e
n
n
u
t
se
cot u
o
ad
p
j
p
a
o
c
s
e
i
n
te
t
Adjacent
Opposite
Hypotenuse
θ
This description of the trigonometric functions has the advantage of being
independent of both the unit circle and the coordinate system in the plane.
EXAMPLE 2
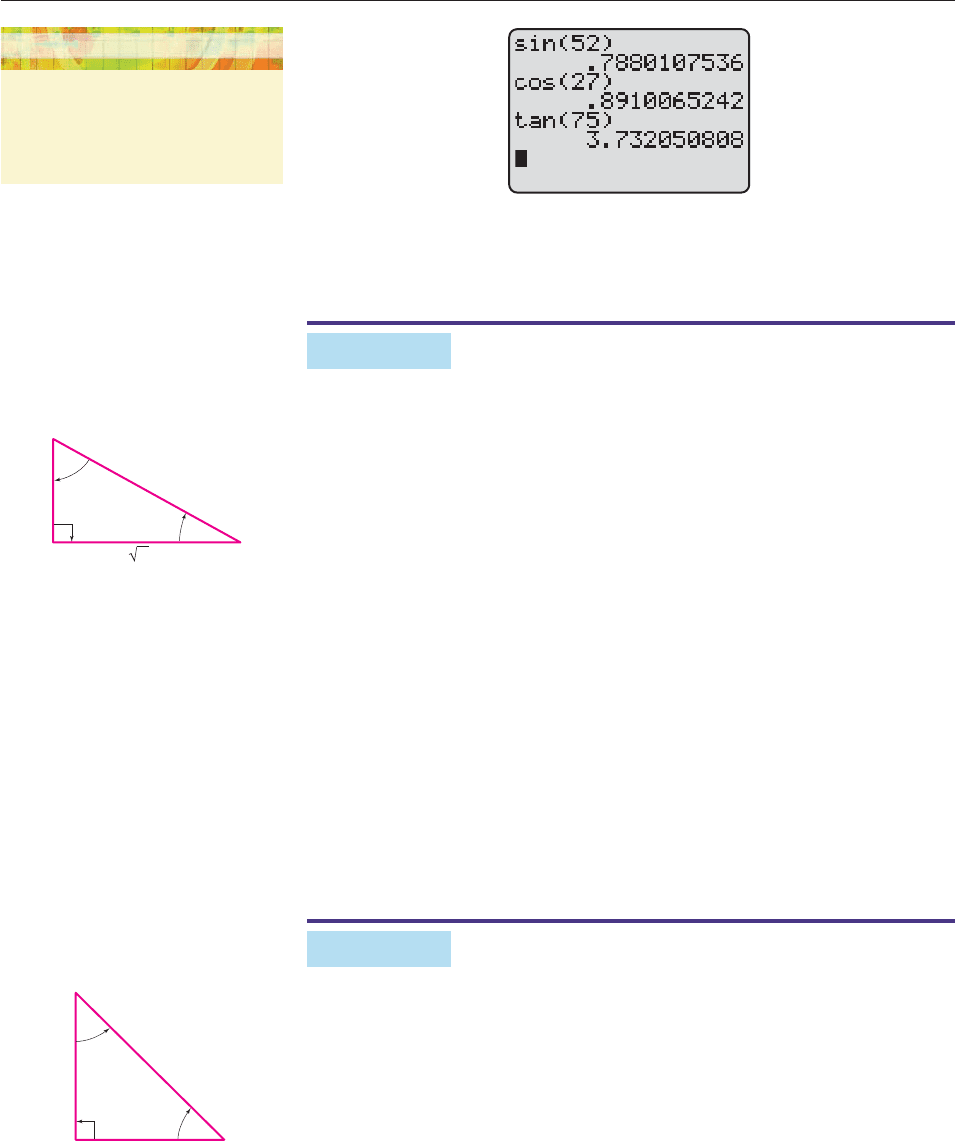
Evaluate sin u, cos u, and tan u for the angle u shown in Figure 8–3.
SOLUTION The side opposite angle u has length 3, and the side adjacent to
angle u has length 4. Hence,
sin u
3
5
cos u
4
5
tan u
3
4
. ■
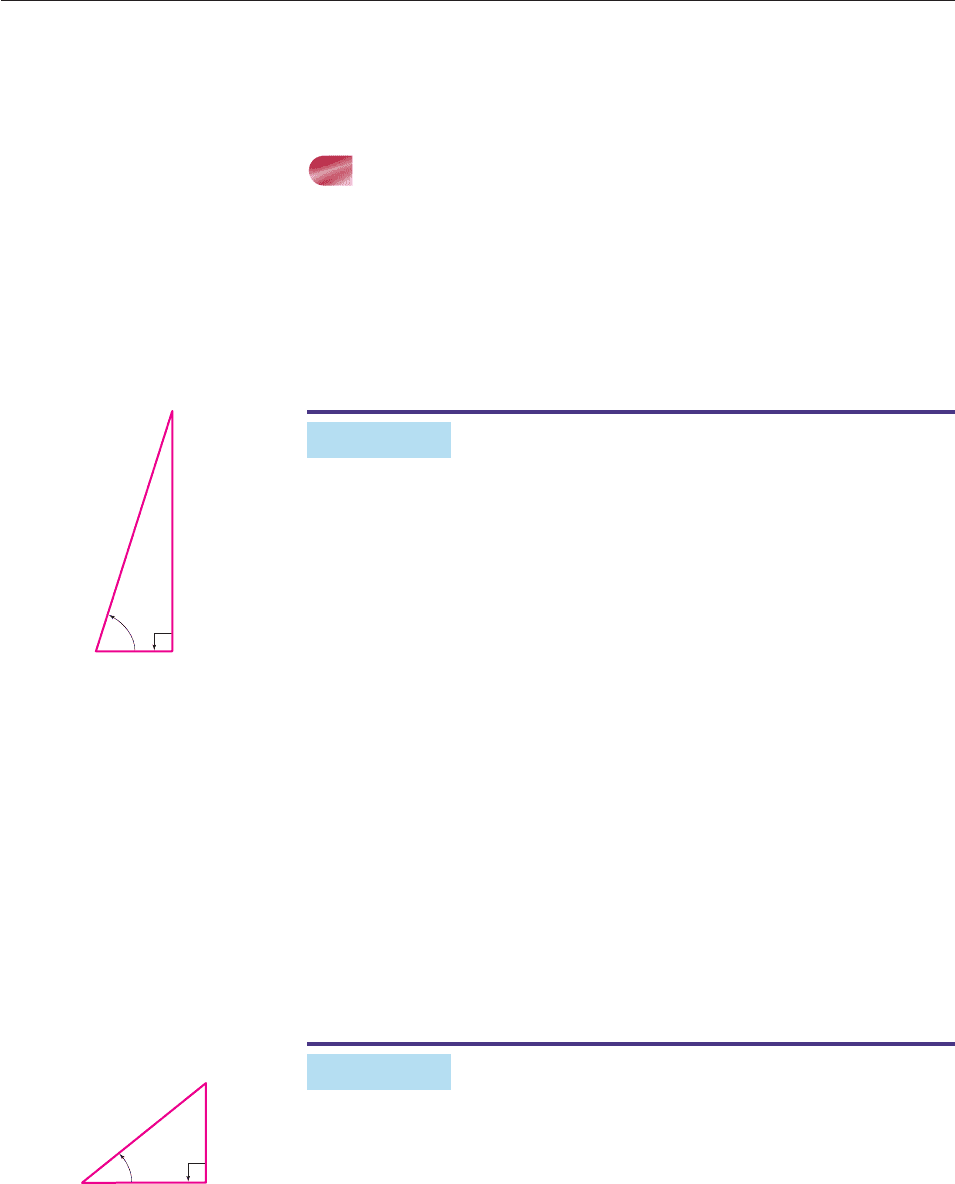
EXAMPLE 3
Evaluate sin u, cos u, and tan u when u is the angle shown in Figure 8–4.
SOLUTION First, we find the length of the third side a by using the
Pythagorean Theorem.
a
2
5
2
13
2
Multiply out terms: a
2
25 169
Subtract 25 from both sides: a
2
144
Take square roots on both sides.* a 144
12.
Now we can calculate the values of the trigonometric functions.
sin u
hy
o
p
p
o
p
t
o
e
s
n
i
u
te
se
1
5
3
, cos u
hy
a
p
d
o
ja
t
c
e
e
n
n
u
t
se
1
1
2
3
,
tan u
o
ad
p
j
p
a
o
c
s
e
i
n
te
t
1
5
2
. ■
Unless you are given an appropriate triangle, whose sides are known (or can
be computed) as in Example 3, it may be difficult to find the exact values of the
trigonometric functions at an angle u. Fortunately, however, your calculator can
provide good approximations, as illustrated in Figure 8–5 on the next page.
length of side opposite angle u
length of side adjacent to angle u
length of side adjacent to angle u
length of hypotenuse
length of side opposite angle u
length of hypotenuse
SECTION 8.1 Trigonometric Functions of Angles 577
5
4
3
θ
Figure 8–3
*The equation a
2
144 has two solutions, 12 and 12, but only the positive one applies here since
a is the side of a triangle.
13
5
a
θ
Figure 8–4
In a few cases, however, we can find the exact values of sine, cosine, and tangent.
EXAMPLE 4
Evaluate sin u, cos u, tan u when (a) u 30° (b) u 60°.
SOLUTION
(a) Consider a 30°-60°-90° triangle whose hypotenuse has length 2. As explained
in Example 3 of the Geometry Review Appendix, the side opposite the 30°
angle must have length 1 (half the hypotenuse) and the side adjacent to
this angle must have length 3
, as shown in Figure 8–6. According to the
right triangle description,
sin 30°
hy
o
p
p
o
p
t
o
e
s
n
i
u
te
se
1
2
, cos 30°
hy
a
p
d
o
ja
t
c
e
e
n
n
u
t
se
2
3
,
tan 30°
o
ad
p
j
p
a
o
c
s
e
i
n
te
t
1
3
3
3
.
(b) The same triangle can be used to evaluate the trigonometric functions at 60°.
In this case, the opposite side has length 3
and the adjacent side has length
1. Therefore,
sin 60°
hy
o
p
p
o
p
t
o
e
s
n
i
u
te
se
2
3
, cos 60°
hy
a
p
d
o
ja
t
c
e
e
n
n
u
t
se
1
2
,
tan 60°
o
ad
p
j
p
a
o
c
s
e
i
n
te
t
1
3
3
. ■
EXAMPLE 5
Evaluate sin 45°, cos 45°, tan 45°.
SOLUTION Consider a 45°-45°-90° triangle whose sides each have length 3
(Figure 8–7). According to the Pythagorean Theorem, the hypotenuse d satisfies
d
2
3
2
3
2
18,
so
d 18 9
2
9
2
3 2
.
Therefore,
sin 45°
hy
o
p
p
o
p
t
o
e
s
n
i
u
te
se
3
3
2
1
2
2
2
578 CHAPTER 8 Triangle Trigonometry
Figure 8–5
TECHNOLOGY TIP
Throughout this chapter, be sure your
calculator is set for DEGREE mode. Use
the MODE(S) menu on TI and HP and
the SETUP menu on Casio.
45°
45°
d
3
3
Figure 8–7
60°
30°
2
1
3
Figure 8–6
cos 45°
hy
a
p
d
o
ja
t
c
e
e
n
n
u
t
se
3
3
2
1
2
2
2
tan 45°
o
ad
p
j
p
a
o
c
s
e
i
n
te
t
3
3
1. ■
SOLVING RIGHT TRIANGLES
Many applications of trigonometry involve “solving a triangle.” This means find-
ing the lengths of all three sides and the measures of all three angles when only
some of these quantities are given. Solving the right triangles depends on this fact.
The right angle description of a trigonometric function
(such as sin u opposite/hypotenuse) relates three quantities:
the angle u and two sides of the right triangle.
When two of these three quantities are known, then the third can always be found.
EXAMPLE 6
Find the lengths of sides b and c in the right triangle shown in Figure 8–8.
SOLUTION Since the side c is opposite the 75° angle and the hypotenuse is 17,
we have
sin 75°
hy
o
p
p
o
p
t
o
e
s
n
i
u
te
se
1
c
7
.
We can solve this equation for c.
1
c
7
sin 75°
Multiply both sides by 17: c 17 sin 75°
Use a calculator (in degree mode) to evaluate sin 75°: c 17(.9659) 16.42.
Side b can now be found by the Pythagorean Theorem or by using the fact that
cos 75°
hy
a
p
d
o
ja
t
c
e
e
n
n
u
t
se
1
b
7
.
Solving this equation and using a calculator shows that
1
b
7
cos 75°
b 17 cos 75° 17(.2588) 4.40. ■
EXAMPLE 7
Solve the right triangle in Figure 8–9.
SOLUTION We must find the measure of ⭿ C and the lengths of sides b and c.
Since the sum of the angles of a triangle is 180°, we have
40° 90° ⭿ C 180°
⭿ C 180° 40° 90° 50°.
SECTION 8.1 Trigonometric Functions of Angles 579
75°
17
c
b
Figure 8–8
4
40°
c
b
B
A
C
Figure 8–9
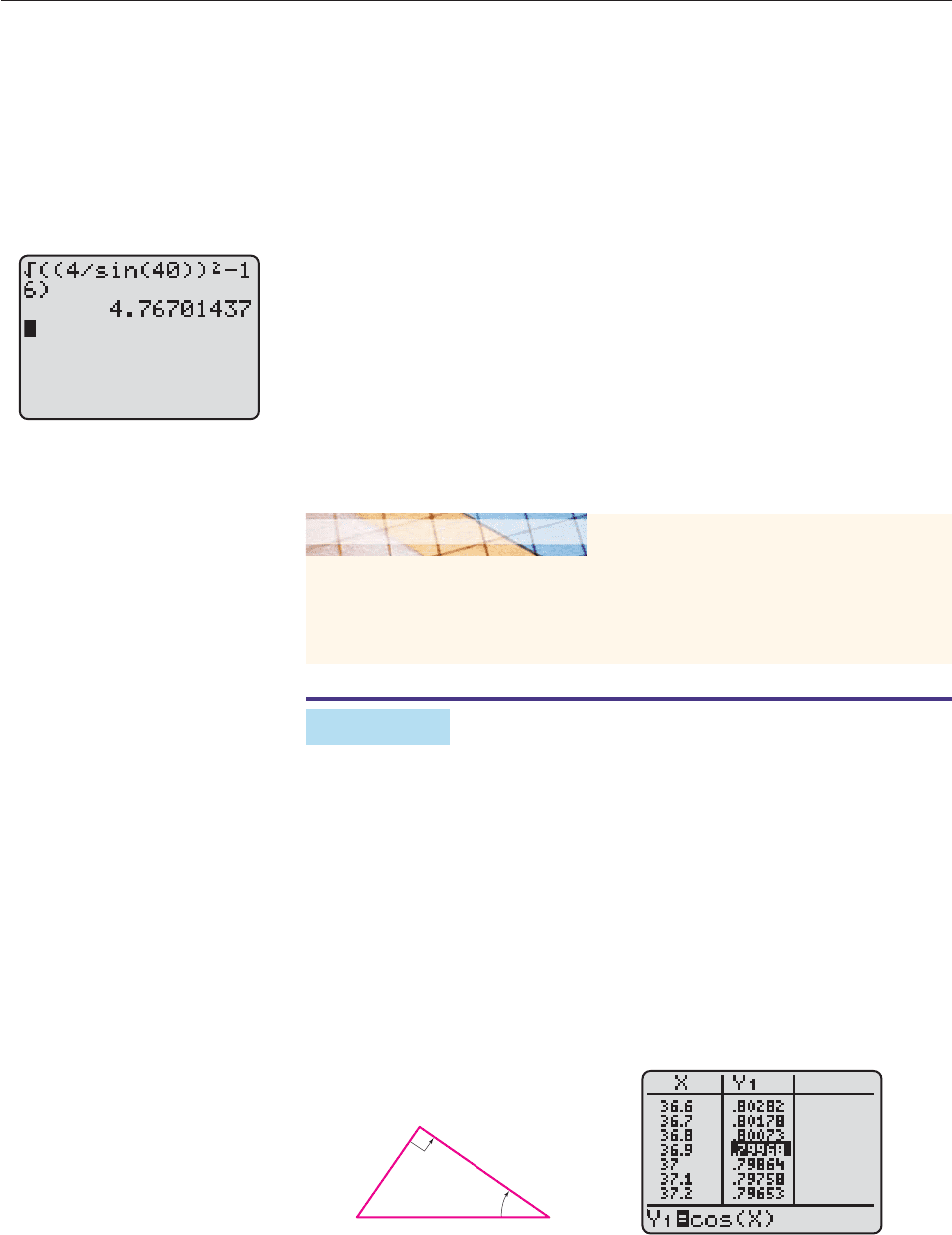
Furthermore, Figure 8–9 shows that
sin A
4
b
Since A 40°: sin 40°
4
b
Multiply both sides by b: b sin 40° 4
Divide both sides by sin 40°: b
sin
4
40°
6.22.
Now side c can be found by using the Pythagorean Theorem.
4
2
c
2
b
2
c
2
b
2
16
c
b
2
1
6
sin
4
40
°
2
16
.
A calculator shows that c 4.77 (Figure 8–10). ■
580 CHAPTER 8 Triangle Trigonometry
Figure 8–10
In Example 7, use the approximation b 6.22 and the Pythagorean Theorem to
find c. Is your answer the same as the length of c found in Figure 8–10? Why not?
The moral here is: Don’t use approximations in intermediate steps if you can avoid
it. However, rounding your final answer is usually appropriate.
CALCULATOR EXPLORATION
EXAMPLE 8
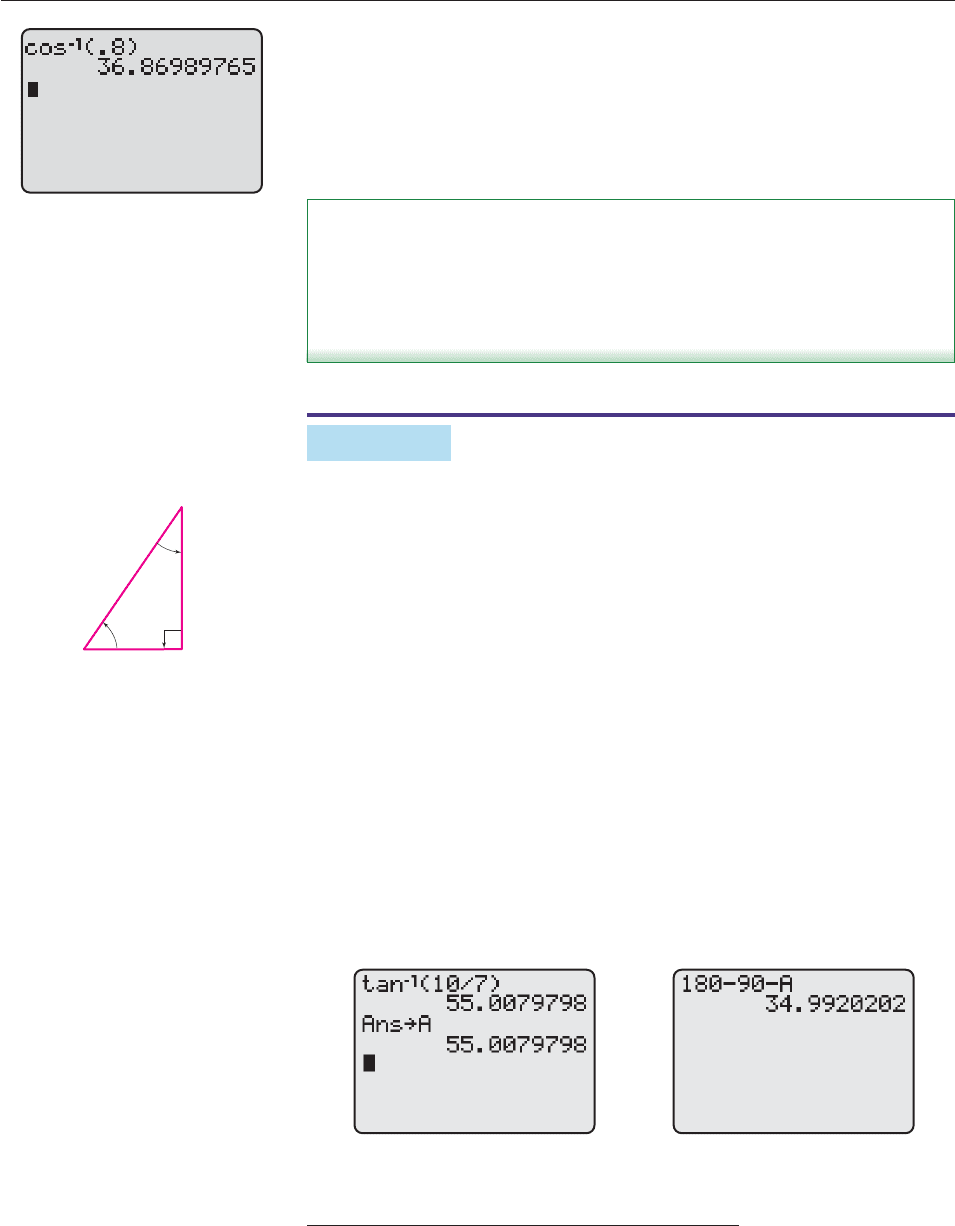
Find the degree measure of the angle u in Figure 8–11.
SOLUTION We first note that
cos u
hy
a
p
d
o
ja
t
c
e
e
n
n
u
t
se
4
5
.8.
Before calculators were available, u was found by using a table of cosine values,
as follows: Look through the column of cosine values for the closest one to .8,
then look in the first column for the corresponding value of u. You can do the
same thing by having your calculator generate a table for y
1
cos x, as in Fig-
ure 8–12. The closest entry to .8 in the cosine ( y
1
) column is .79968, which
corresponds to an angle of 36.9°. Hence, u 36.9°.
Figure 8–11 Figure 8–12
4
5
3
θ
SECTION 8.1 Trigonometric Functions of Angles 581
NOTE
In this chapter, we shall use the COS
1
key, and the analogous keys SIN
1
and TAN
1
, as they were
used in the preceding example: as a way to find an angle u in a triangle, when sin u or cos u or tan u
is known. The other uses of these keys are discussed in Section 7.4, which deals with the inverse
functions of sine, cosine, and tangent.
EXAMPLE 9
Without using the Pythagorean Theorem, find angles a and b and side c of the
triangle in Figure 8–14. Make your answers as accurate as your technology
allows.
SOLUTION We first note that
tan a
o
ad
p
j
p
a
o
c
s
e
i
n
te
t
1
7
0
.
We use the TAN
1
key on a calculator to approximate a and store the result
a 55.0079798°
in memory A (Figure 8–15).* Since the sum of the angles of a triangle is 180°, we
have
a b 90° 180°
b 180° 90° a.
Using a calculator and the stored value of a, we see that b 34.9920202°
(Figure 8–16).
Figure 8–15
Figure 8–16
10
7
c
α
β
Figure 8–14
*We are using a TI-84. Other calculators and computer programs may give answers with a different
degree of accuracy. For instance, a TI-89 gives a 55.0079798014°.
Figure 8–13
A faster, more accurate method of finding u is to use the COS
1
key on your
calculator (labeled ACOS on some models). When you key in COS
1
.8, as in
Figure 8–13, the calculator produces an acute angle whose cosine is .8, namely,
u 36.8699°. Thus, the COS
1
key provides the electronic equivalent of search-
ing the cosine table, without actually having to construct the table. ■

Finally, we use the fact that
sin a
hy
o
p
p
o
p
t
o
e
s
n
i
u
te
se
1
c
0
.
Multiplying both ends of this equation by c shows that
c sin a 10
c
si
1
n
0
a
.
Using a calculator and the stored value of a, we find that c 12.20655562
(Figure 8–17). ■
582 CHAPTER 8 Triangle Trigonometry
Figure 8–17
EXERCISES 8.1
Directions: When solving triangles here, all decimal approxi-
mations should be rounded off to one decimal place at the end
of the computation.
In Exercises 1–6, evaluate the trigonometric functions at the
angle (in standard position) whose terminal side contains the
given point.
1. (2, 3) 2. (4, 2) 3. (3, 7)
4. (2
, 3
) 5. (3, 2
) 6. (3, 5)
In Exercises 7–12, find sin u, cos u, tan u.
7.
8.
9.
7
3
2
θ
5
5
2
5
θ
3
2
11
θ
10.
11.
12.
In Exercises 13–18, find side c of the right triangle in the figure
under the given conditions.
13. cos A 12/13 and b 39
14. sin C 3/4 and b 12
15. tan A 5/12 and a 15
16. sec A 2 and b 8
17. cot A 6 and a 1.4
18. csc C 1.5 and b 4.5
a
b
c
C
B
A
t
1
θ
1 + t
2
m
h
d
θ
17
8
15
θ
In Exercises 19–24, find the length h of the side of the right
triangle, without using a calculator.
19.
20.
21.
22.
23.
24.
In Exercises 25–28, find the required side without using a
calculator.
c
b
a
C
A
B
20
h
60°
30°
100
h
12
45°
h
h
150
30°
h
72
60°
25
45°
h
SECTION 8.1 Trigonometric Functions of Angles 583
25. a 4 and angle A measures 60°; find c.
26. c 5 and angle A measures 60°; find a.
27. c 10 and angle A measures 30°; find a.
28. a 12 and angle A measures 30°; find c.
In Exercises 29–36, use the figure for Exercises 25–28. Solve
the right triangle under the given conditions.
29. b 10 and ⭿C 40°
30. c 12 and ⭿C 37°
31. a 16 and ⭿A 14°
32. a 8 and ⭿A 40°
33. c 5 and ⭿A 65°
34. c 4 and ⭿C 28°
35. b 3.5 and ⭿A 72°
36. a 4.2 and ⭿C 33°
In Exercises 37–40, find angle u.
37.
38.
39.
40.
In Exercises 41–48, use the figure for Exercises 25–28 to find
angles A and C under the given conditions.
41. a 8 and c 15
42. b 14 and c 5
200
144
θ
3
2
θ
10
12
θ
4
3
θ

43. a 7 and b 10
44. a 7 and c 3
45. b 18 and c 12
46. a 4 and b 9
47. a 2.5 and c 1.4
48. b 3.7 and c 2.2
49. Let u be an acute angle with sides a and b in a triangle, as in
the figure below.
(a) Find the area of the triangle (in terms of h and a).
(b) Find sin u.
(c) Use part (b) to show that h b sin u.
(d) Use parts (a) and (c) to show that the area A of a trian-
gle in which an acute angle u has sides a and b is
A
1
2
ab sin u.
In Exercises 50–54, use the result of Exercise 49 to find the
area of the given triangle.
50.
51.
25°
14
10
65°
8
4
a
b
h
θ
584 CHAPTER 8 Triangle Trigonometry
52.
53.
54.
55.
Let u and a be acute angles of a right triangle, as shown in
the figure.
(a) Find sin u and cos a.
(b) Explain why u a 90°.
(c) Use parts (a) and (b) to conclude that for any acute
angle u,
cos(90° u) sin u.
56. (a) Using the figure for Exercise 55, find cos u and sin a.
(b) Use part (a) and part (b) of Exercise 55 to show that for
any acute angle u,
sin(90° u) cos u.
This equation and the one in Exercise 55(c) are called
cofunction identities.
c
a
b
θ
α
38°
12
9
30°
44
20
59°
140
72
8.1 ALTERNATE Trigonometric Functions of Angles
■ Use right triangles to evaluate the trigonometric functions of
acute angles.
■ Use the point-in-the-plane description to evaluate trigonometric
functions of any angle.
Before reading this section, it might be a good idea to read the Geometry Review
Appendix, which presents the basic facts about angles and triangles that fre-
quently are used here. In particular, recall that a right triangle is one that contains
a right angle, that is, an angle of 90°. An acute angle is an angle whose measure
is less than 90°. Consider the right triangles in Figure 8–18, each of which has an
acute angle of u degrees.
Section Objectives
NOTE
If you have read Chapter 6, omit this
section. If you have not read Chapter 6,
use this section in place of Section 8.1.
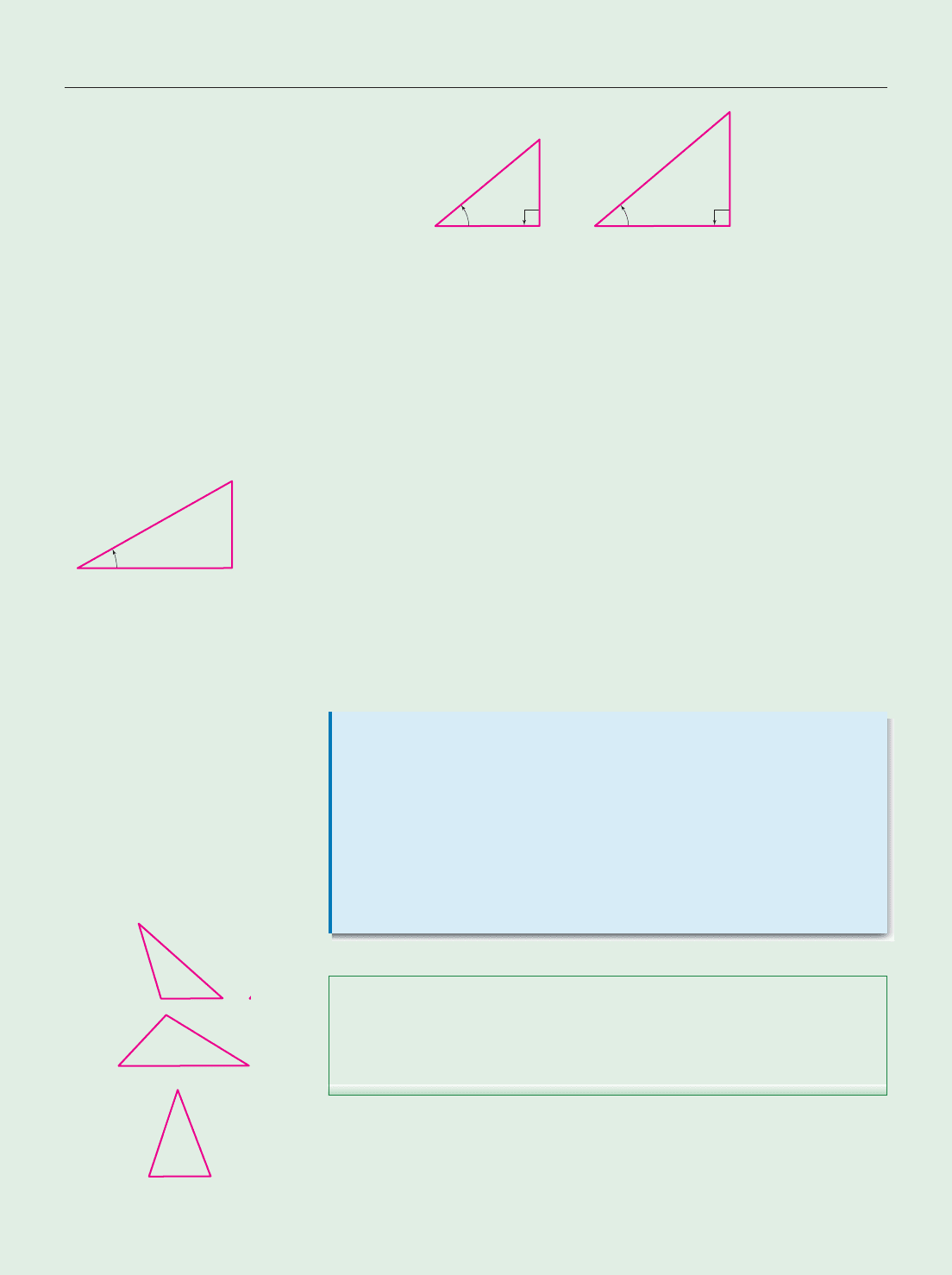
Since the sum of the angles of any triangle is 180°, we see that the third angle
in each of these triangles has the same measure, namely, 180° 90° u. Thus,
both triangles have equal corresponding angles and, therefore, are similar.
Consequently, by the Ratios Theorem of the Geometry Review Appendix, we
know that the ratio of corresponding sides is the same, that is
a
c
a
c
.
Each of these fractions is the ratio
,
as indicated in Figure 8–19. Consequently, this ratio depends only on the angle u
and not on the size of the triangle. Similar remarks apply to the ratios of other
sides of the triangle in Figure 8–19 and make it possible to define three new func-
tions. For each function, the input is an acute angle u, and the corresponding out-
put is a ratio of sides in any right triangle containing angle u, as summarized here.
length of the side opposite angle u
length of the hypotenuse
ALTERNATE 8.1 Trigonometric Functions of Angles 585
c
a
θ
c
′
a
′
θ
Figure 8–18
Side adjacent
to angle
Side
opposite
angle
Hypotenuse
θ
θ
θ
Figure 8–19
Trigonometric Functions
of Acute Angles
Name of Abbre-
Function viation Rule of Function
sine sin sin u
cosine cos cos u
tangent tan tan u
length of side opposite angle u
length of side adjacent to angle u
length of side adjacent to angle u
length of hypotenuse
length of side opposite angle u
length of hypotenuse
NOTE
Now turn to page 577 and begin reading at Example 2. When you have finished Example 9 on
page 582, return here and continue reading below. [If you prefer, you can delay reading the mate-
rial below until Section 8.3, where it will first be used.]
The preceding discussion applies only to right triangles. The next step is to
learn how to solve other triangles, such as those in Figure 8–20. To do this, we
must find a description of the trigonometric functions that is not limited to acute
angles of a right triangle. First, we introduce some terminology.
Figure 8–20
