Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

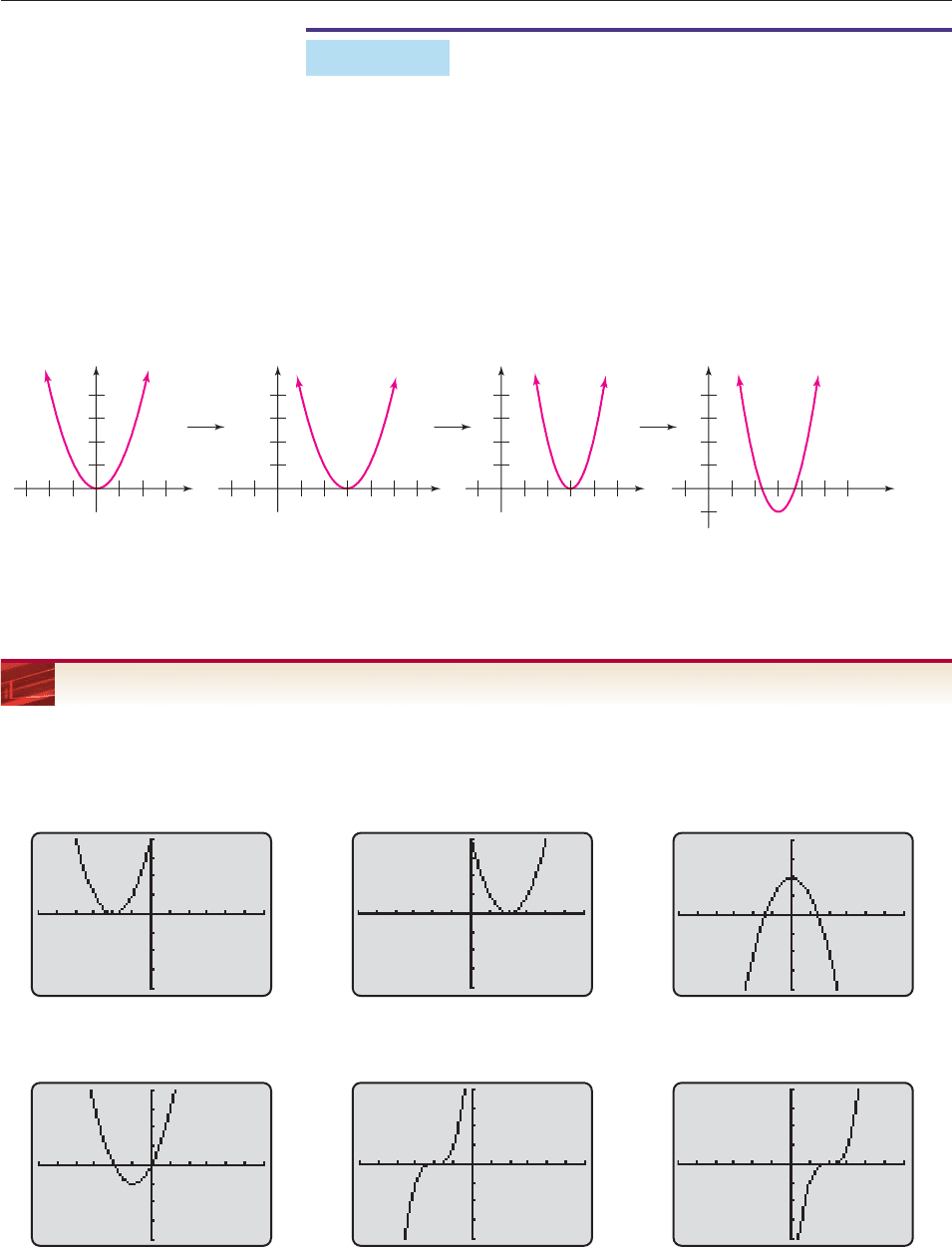
EXAMPLE 4
To understand the graph of g(x) 2(x 3)
2
1, note that the rule of g may be
obtained from the rule of f (x) x
2
in three steps:
Step 1 Step 2 Step 3
f (x) x
2
—– (x 3)
2
—– 2(x 3)
2
—– 2(x 3)
2
1 g(x).
Step 1 shifts the graph of f horizontally 3 units to the right; step 2 stretches the
resulting graph away from the x-axis by a factor of 2; step 3 shifts this graph 1 unit
downward, thus producing the graph of g in Figure 3–46. ■
Figure 3–46
f(x) = x
2
g(x) = 2(x − 3)
2
− 1
−3 −2 −11
Step 1 Step 2
23
1
x
y
(x − 3)
2
123
1
456
x
y
2(x − 3)
2
1
Step 3
2345
1
x
y
−1
123
1
456
x
y
186 CHAPTER 3 Functions and Graphs
EXERCISES 3.4
In Exercises 1–8, use the catalog of functions at the end of Section 3.3 and information from this section to match each function with
its graph, which is one of A–L.
4
−4
−66
4
−4
−66
4
−4
−66
4
−4
−66
4
−4
−66
4
−4
−66
A. B. C.
D. E. F.
4
−4
−66
4
−4
−66
4
−4
−66
4
−4
−66
4
−4
−66
4
−4
−66
SECTION 3.4 Graphs and Transformations 187
1. f (x) x
2
2 2. f (x) x 2
3. g(x) (x 2)
3
4. g(x) (x 2)
2
5. f (x) x
6. f (x) (x 1)
2
1
7. g(x) x
2
2 8. g(x) x
3
2
9. The figure shows the graphs of f(x) 2, 2f(x), and f(x 1).
Sketch a graph of the function f.
10. Fill in the entries in the following table
x
y
2244
2
2
4
4
11. Fill in the entries in the following table. If it is impossible to
fill in an entry, put an X in it.
In Exercises 12–15, use the graph of y x and information
from this section (but not a calculator) to sketch the graph of
the function.
12. f(x) x 2 13. g(x) x 2
14. g(x) x 15. f(x) x 2 2
In Exercises 16–19, find a single viewing window that shows
complete graphs of the functions f, g, and h.
16. f (x) .25x
3
9x 5; g(x) f (x) 15;
h(x) f (x) 20
17. f (x)
x
2
9
5; g(x) 3f (x);
h(x) .5f (x)
18. f (x) x
2
5; g(x) f (x 8);
h(x) f (x 6)
19. f (x) .125x
3
.25x
2
1.5x 5;
g(x) f (x) 5; h(x) 5 f (x)
xf(x) g(x) f(x) 2 h(x)
1
2
f(x) i(x) 3f(x) 2
1 1/2
01
12
26
38
tf(t) g(t) f(t) 3 h(t) 4 f(t) i(t) f (t 1) 2
23
16
08
10
25
G. H. I.
J. K. L.
In Exercises 20 and 21, find complete graphs of the functions
f and g in the same viewing window.
20. f (x)
4
x
2
5x
1
2
; g(x) f (x)
21. f (x) x
4
4x
3
2x
2
3; g(x) f (x)
In Exercises 22–25, describe a sequence of transformations
that will transform the graph of the function f into the graph
of the function g.
22. f(x) x
2
x; g(x) (x 3)
2
(x 3) 2
23. f(x) x
2
5; g(x) (x 2)
2
10
24. f(x)
x
3
5
; g(x)
1
2
x
3
5
6
25. f (x)
x
4
x
2
1
; g(x) 10
4x
4
4x
2
4
In Exercises 26–29, write the rule of a function g whose graph
can be obtained from the graph of the function f by performing
the transformations in the order given.
26. f(x) x
2
2; shift the graph horizontally 5 units to the left
and then vertically upward 4 units.
27. f(x) x
2
x 1; reflect the graph in the x-axis, then shift
it vertically upward 3 units.
28. f(x) x
; shift the graph horizontally 6 units to the right,
stretch it away from the x-axis by a factor of 2, and shift it
vertically downward 3 units.
29. f(x) x
; shift the graph horizontally 3 units to the left,
then reflect it in the x-axis, and shrink it toward the
x-axis by a factor of 1/2.
30. Let f (x) x
2
3x, and let g(x) f (x) 2.
(a) Write the rule of g(x).
(b) Find the difference quotients of f (x) and g(x). How are
they related?
31. Let f (x) x
2
5, and let g(x) f (x 1).
(a) Write the rule of g(x) and simplify.
(b) Find the difference quotients of f (x) and g(x).
(c) Let d(x) denote the difference quotient of f (x). Show
that the difference quotient of g(x) is d(x 1).
In Exercises 32–35, use the graph of the function f in the figure
to sketch the graph of the function g.
32. g(x) f (x) 3 33. g(x) f (x) 1
34. g(x) 3f (x) 35. g(x) .25f (x)
x
y
188 CHAPTER 3 Functions and Graphs
In Exercises 36–39, use the graph of the function f in the figure
to sketch the graph of the function h.
36. h(x) f (x) 37. h(x) 4f (x)
38. h(x) f (x) 39. h(x) f (x) 2
In Exercises 40–45, use the graph of the function f in the figure
to sketch the graph of the function g.
40. g(x) f (x 3) 41. g(x) f (x 2)
42. g(x) f (x 2) 3 43. g(x) f (x 1) 3
44. g(x) 2 f (x) 45. g(x) f (x) 2
46. Graph f(x) x 3 x 17 20 in the window with
0 x 20 and 2 y 12. Think of the x-axis as a table
and the graph as a side view of a fast-food carton placed
upside down on the table (the flat part of the graph is the bot-
tom of the carton). Find the rule of a function g whose graph
(in this viewing window) looks like another fast-food carton,
which has been placed right side up on top of the first one.
47. A factory has a linear cost function c(x) ax b, where b
represents fixed costs and a represents the variable costs
(labor and materials) of making one item, both in thousands
of dollars.
(a) If property taxes (part of the fixed costs) are increased
by $35,000 per year, what effect does this have on the
graph of the cost function?
(b) If variable costs increase by 12 cents per item, what
effect does this have on the graph of the cost function?
In Exercises 48–50, assume f (x) (.2x)
6
4. Use the standard
viewing window to graph the functions f and g on the same
screen.
48. g(x) f (2x) 49. g(x) f (3x) 50. g(x) f (4x)
51. On the basis of the results of Exercises 48–50, describe the
transformation that transforms the graph of a function f (x)
x
y
x
y

into the graph of the function f (cx), where c is a constant
with c 1. [Hint: How are the two graphs related to the
y-axis? Stretch your mind.]
In Exercises 52–55, assume f (x) x
2
3. Use the standard
viewing window to graph the functions f and g on the same
screen.
52. g(x) f
1
2
x
53. g(x) f
1
3
x
54. g(x) f
1
4
x
55. g(x) f
1
1
0
x
56. On the basis of the results of Exercises 52–55, describe the
transformation that transforms the graph of a function f (x) into
the graph of the function f (cx), where c is a constant with 0
c 1. [Hint: How are the two graphs related to the y-axis?]
In Exercises 57–60, use the standard viewing window to graph
the function f and the function g(x) f (x) on the same screen.
57. f (x) x 4 58. f (x) x
3
3
59. f (x) .5(x 4)
2
9 60. f (x) x
3
2x
61. On the basis of the results of Exercises 57–60, describe the
relationship between the graph of a function f (x) and the
graph of the function f (x).
In Exercises 62–65, use the standard viewing window to graph
the function f and the function g(x) f (x) on the same
screen. Exercise 66 may be helpful for interpreting the results.
SPECIAL TOPICS 3.4.A Symmetry 189
62. f (x) .5x
2
5 63. f (x) x
3
4x
2
x 3
64. f (x) x 3 65. f (x) x
3
2x
66. (a) Let f be a function, and let g be the function defined by
g(x) f (x). Use the definition of absolute value
(page 9) to explain why the following statement is true:
f (x)iff (x) 0
g(x)
f (x)iff (x) 0
(b) Use part (a) and your knowledge of transformations to
explain why the graph of g consists of those parts of the
graph of f that lie above the x-axis together with the re-
flection in the x-axis of those parts of the graph of f that
lie below the x-axis.
67. Because of a calculator’s small screen size, it is not always
easy (or even possible!) to find a viewing window that
displays what its user desires.
(a) Graph f(x) x
2
x 6 in the standard viewing win-
dow. Let h(x) f(x 1000). What should h(x) look like?
(b) Find an appropriate viewing window for the graph of h(x).
(c) Try to find a viewing window that clearly displays both
the graph of f and the graph of h. What makes this prob-
lem difficult?
(d) Let g(x) 1000 f(x). What should g(x) look like?
(e) Find an appropriate viewing window for the graph of
g(x). Can you find a viewing window that clearly dis-
plays both the graph of f and the graph of g?
3.4.A SPECIAL TOPICS Symmetry
■ Recognize symmetries of a graph with respect to the x- and
y-axes and the origin.
■ Identify even and odd functions, given a formula or a graph.
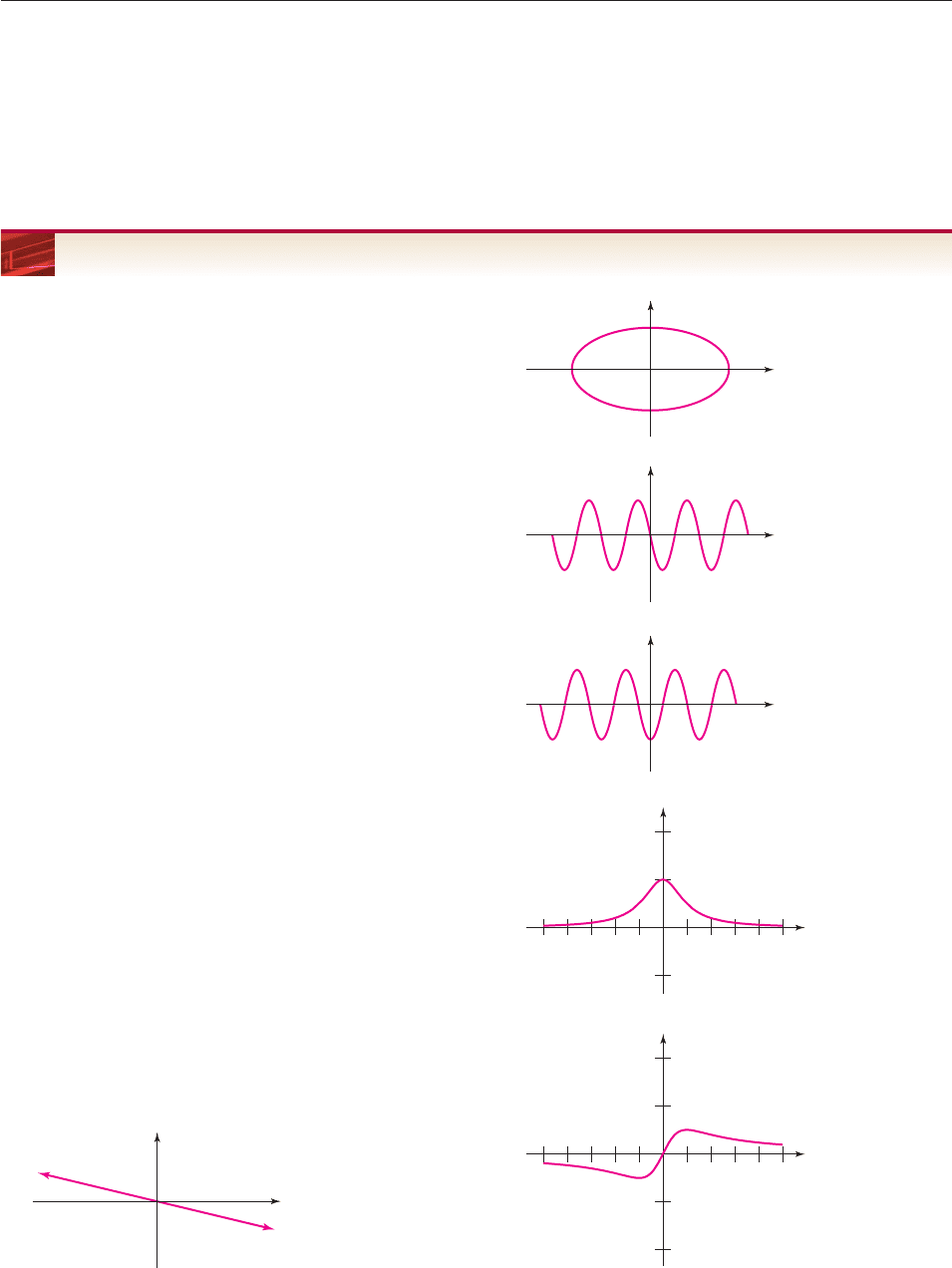
A graph is symmetric with respect to the y-axis if the part of the graph on the
right side of the y-axis is the mirror image of the part on the left side of the y-axis
(with the y-axis being the mirror), as shown in Figure 3–47.
Figure 3–47
x
2
+ 4y
2
= 24y
(−6, 3) (6, 3)
(−x, y)(x, y)
x
y
P
Q
Section Objectives

Each point P on the left side of the graph has a mirror image point Q on the right
side of the graph, as indicated by the dashed lines. Note that:
Their second coordinates are the same (P and Q are on the same side of the
x-axis and the same distance from it);
Their first coordinates are negatives of each other (P and Q lie on opposite
sides of the y-axis and the same distance from it).
Thus, a graph is symmetric with respect to the y-axis provided that
Whenever (x, y) is on the graph, then (⫺x, y) is also on it.
In algebraic terms, this means that replacing x by x in the equation leads to the
same number y. In other words, replacing x by x produces an equivalent equation.
EXAMPLE 1
Replacing x by x in the equation y x
4
5x
2
3 produces
y (x)
4
5(x)
2
3,
which is the same equation because (x)
2
x
2
and (x)
4
x
4
. Therefore, the
graph is symmetric with respect to the y-axis.
190 CHAPTER 3 Functions and Graphs
Confirm this fact by graphing the equation y x
4
5x
2
3.
■
GRAPHING EXPLORATION
x-AXIS SYMMETRY
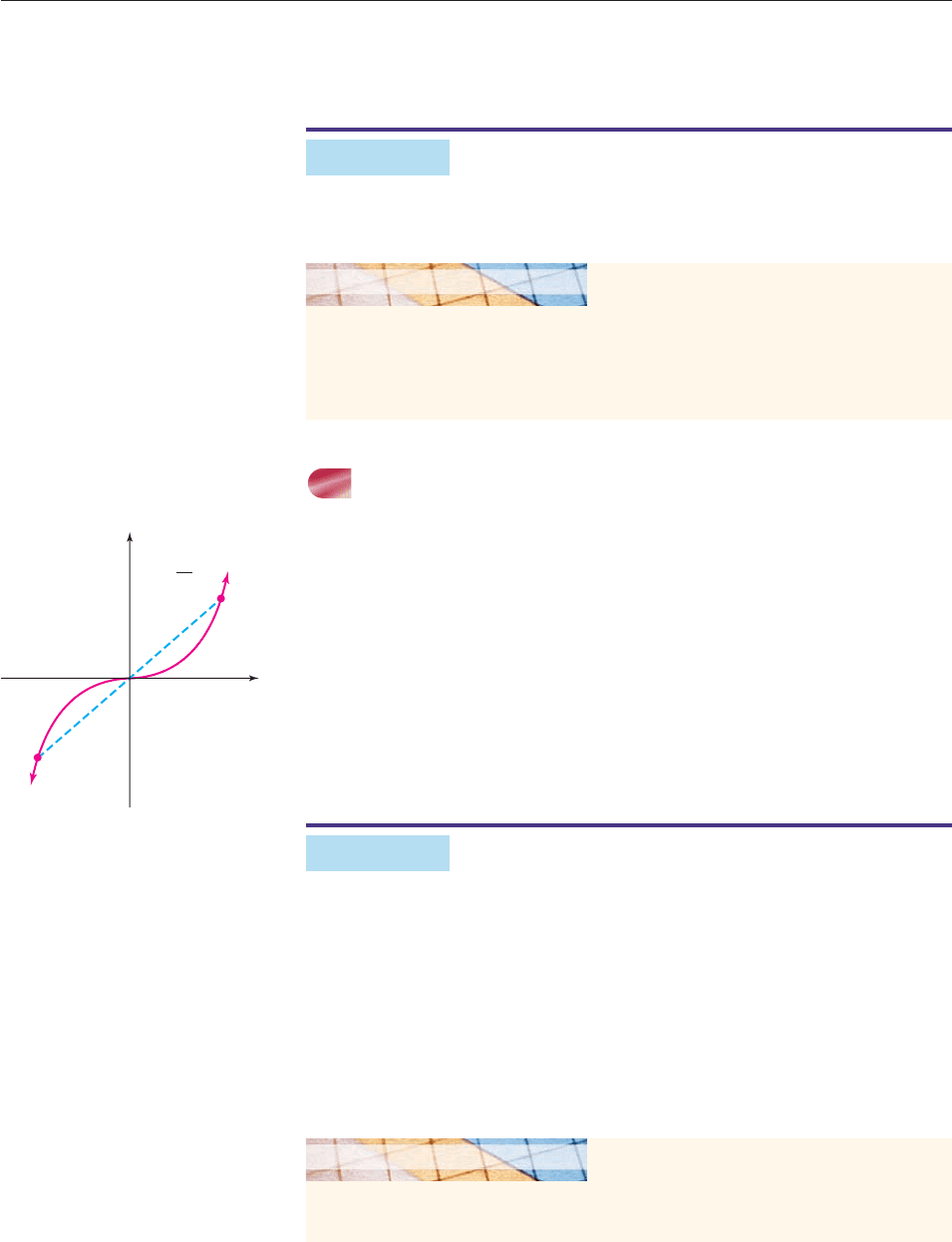
A graph is symmetric with respect to the x-axis if the part of the graph above the
x-axis is the mirror image of the part below the x-axis (the x-axis being the mirror),
as shown in Figure 3–48.
Figure 3–48
Using Figure 3–48 and argument analogous to the one preceding Example 1,
we see that a graph is symmetric with respect to the x-axis provided that
Whenever (x, y) is on the graph, then (x, ⫺y) is also on it.
x = y
2
− 3
(x, y)
(x, −y)
(2,
(2, −
5)
x
y
P
Q
5)
In algebraic terms, this means that replacing y by y in the equation leads to
the same number x. In other words, replacing y by y produces an equivalent
equation.
EXAMPLE 2
Replacing y by y in the equation y
2
4x 12 produces (y)
2
4x 12,
which is the same equation, so the graph is symmetric with respect to the x-axis.
ORIGIN SYMMETRY
A graph is symmetric with respect to the origin if a straight line through the ori-
gin and any point P on the graph also intersects the graph at a point Q such that
the origin is the midpoint of segment PQ, as shown in Figure 3–49.
Here is a way to visualize origin symmetry: Picture hammering a nail into the
origin and rotating the graph 180°. If the graph winds up looking the same, then it
is symmetric about the origin.
Using Figure 3–49, we can also describe symmetry with respect to the origin
in terms of coordinates and equations (as proved in Exercise 38):
Whenever (x, y) is on the graph, then (⫺x, ⫺y) is also on it.
In algebraic terms, this means that replacing x by x and y by y in the equation
produces an equivalent equation.
EXAMPLE 3
Replacing x with x and y with y in the equation y
1
x
0
3
x yields
y
(
10
x)
3
(x)
y
1
x
0
3
x
y
1
x
0
3
x
Therefore the graph of y
1
x
0
3
x is symmetric with respect to the origin.
SPECIAL TOPICS 3.4.A Symmetry 191
(x, y)
(−x, −y)
O
P
Q
x
3
4
x
y
y =
Figure 3–49
Confirm this fact by graphing the equation. To do this, note that every point
on the graph of y
2
4x 12 is also on the graph of either y
4x 1
2
or
y
4x 1
2
. Each of these latter equations defines a function; graph them
both on the same screen.
■
GRAPHING EXPLORATION
Confirm this fact by graphing the equation y
1
x
0
3
x.
■
GRAPHING EXPLORATION
Here is a summary of the various tests for symmetry:
EVEN AND ODD FUNCTIONS
For functions, the algebraic description of symmetry takes a different form.
A function f whose graph is symmetric with respect to the y-axis is called an
even function. To say that the graph of y f (x) is symmetric with respect to the
y-axis means that replacing x by x produces the same y value. In other words,
the function takes the same value at both x and x. Therefore,
For example, f (x) x
4
x
2
is even because
f (x) (x)
4
(x)
2
x
4
x
2
f (x).
Thus, the graph of f is symmetric with respect to the y-axis, as you can easily ver-
ify with your calculator (do it!).
Except for zero functions ( f (x) 0 for every x in the domain), the graph of
a function is never symmetric with respect to the x-axis. The reason is the vertical
line test: The graph of a function never contains two points with the same first co-
ordinate. If both (5, 3) and (5, 3), for instance, were on the graph, this would say
that f (5) 3 and f (5) 3, which is impossible when f is a function.
A function whose graph is symmetric with respect to the origin is called an
odd function. If both (x, y) and (x, y) are on the graph of such a function f,
then we must have both
y f (x) and y f (x),
so f (x) y f (x). Therefore,
192 CHAPTER 3 Functions and Graphs
Symmetry
Tests
Symmetry with Coordinate Test Algebraic Test
Respect to for Symmetry for Symmetry
y-axis (x, y) on graph implies Replacing x by x produces
(x, y) on graph. an equivalent equation.
x-axis (x, y) on graph implies Replacing y by y produces
(x, y) on graph. an equivalent equation.
origin (x, y) on graph implies Replacing x by x and y by
(x, y) on graph. y produces an equivalent
equation.
Even
Functions
A function f is even provided that
f (x) f (x) for every number x in the domain of f.
The graph of an even function is symmetric with respect to the y-axis.
Odd
Functions
A function f is odd provided that
f (x) f (x) for every number x in the domain of f.
The graph of an odd function is symmetric with respect to the origin.
For example, f (x) x
3
is an odd function because
f (x) (x)
3
x
3
f (x).
Hence, the graph of f is symmetric with respect to the origin (verify this with your
calculator).
SPECIAL TOPICS 3.4.A Symmetry 193
EXERCISES 3.4.A
In Exercises 1–4, sketch the graph of the equation. If the graph
is symmetric with respect to the x-axis, the y-axis, or the origin,
say so.
1. y x
2
2 2. x ( y 3)
2
3. y x
3
2 4. y (x 2)
3
In Exercises 5–16, determine whether the given function is
even, odd, or neither.
5. f (x) 4x 6. k(t) 5t
7. f (x) x
2
x 8. h(u) 3u
9. k(t) t
4
6t
2
5
10. f (x) x(x
4
x
2
) 4
11. f (x) x(x
4
x
2
) 4x
12. f(t)
t
2
5
13. h(x)
7 2x
2
14. f (x)
x
x
2
7
2
15. g(x)
x
x
2
2
1
1
16. L(a)
In Exercises 17–20, determine algebraically whether or not the
graph of the given equation is symmetric with respect to the
x-axis.
17. x
2
6x y
2
8 0
18. x
2
8x y
2
15
19. x
2
2x y
2
2y 2
20. x
2
x y
2
y 0
In Exercises 21–28, determine whether the given graph is
symmetric with respect to the y-axis, the x-axis, or the
origin.
21.
x
y
a
a
22.
23.
24.
25.
26.
x
y
2244
1
2
1
2
x
y
2244
1
1
2
x
y
x
y
x
y

32. Odd
33. (a) Draw some coordinate axes, and plot the points (0, 1),
(1, 3), (5, 2), (3, 5), (2, 3), and (4, 1).
(b) Suppose the points in part (a) lie on the graph of an even
function f. Plot the points (0, f (0)), (1, f (1)),
(5, f (5)), (3, f (3)), (2, f (2)), and (4, f (4)).
34. Draw the graph of an even function that includes the
points (0, 3), (3, 0), (2, 0), (1, 4), (2.5, 1), (4, 3),
and (5, 3).*
35. (a) Plot the points (0, 0); (2, 3); (3, 4); (5, 0); (7, 3);
(1, 1); (4, 1); (6, 1).
(b) Suppose the points in part (a) lie on the graph of an
odd function f. Plot the points (2, f (2));
(3, f (3)); (5, f (5)); (7, f (7)); (1, f (1));
(4, f (4)); (6, f (6)).
(c) Draw the graph of an odd function f that includes all the
points plotted in parts (a) and (b).*
36. Draw the graph of an odd function that includes the points
(3, 5), (1, 1), (2, 6), (4, 9), and (5, 5).*
37. Show that any graph that has two of the three types of sym-
metry (x-axis, y-axis, origin) necessarily has the third type
also.
38. Use the midpoint formula to show that (0, 0) is the midpoint
of the segment joining (x, y) and (x, y). Conclude that
the coordinate test for symmetry with respect to the origin
(page 192) is correct.
THINKER
39. In the first half of 2005, Ford Motor company spent
768 million dollars on advertising. Presumably, if they had
spent more money, they would have sold more cars, and if
they had spent less money, they would have sold fewer cars.
Let x be the change in their advertising budget for the first
half of 2006, in millions of dollars. If x is 10, that would cor-
respond to Ford spending 778 million dollars, for example,
and if x is 10 then that corresponds to Ford spending
758 million.
Let f(x) be the number of cars that Ford sells in the first
half of 2006, with 100 x 100.
(a) Would it be realistic for f (x) to be an even function?
Why or why not?
(b) Would it be realistic for f(x) to be an odd function? Why
or why not?
x
y
27.
28.
In Exercises 29–32, complete the graph of the given function,
assuming that it satisfies the given symmetry condition.
29. Even
30. Even
31. Odd
x
y
x
y
x
y
x
y
x
y
2244
2
2
4
6
194 CHAPTER 3 Functions and Graphs
*There are many correct answers.

SECTION 3.5 Operations on Functions 195
3.5 Operations on Functions
Section Objectives
■ Find the sum, difference, product, and quotient of two
functions.
■ Compose functions to create a new function.
■ Write a function as the composite of two or more
functions.
We now examine ways in which two or more given functions can be used to cre-
ate new functions. If f and g are functions, then their sum is the function h defined
by the rule
h(x) f (x) g(x).
For example, if f (x) 3x
2
x and g(x) 4x 2, then
h(x) f (x) g(x)
(3x
2
x) (4x 2)
3x
2
5x 2.
Instead of using a different letter h for the sum function, we shall usually denote
it by f g. Thus, the sum f g is defined by the rule
( f g)(x) f (x) g(x).
This rule is not just a formal manipulation of symbols. If x is a number, then so are
f (x) and g(x). The plus sign in f (x) g(x) is addition of numbers, and the result is
a number. But the plus sign in f g is addition of functions, and the result is a new
function.
The difference f g is the function defined by the rule
( f g)(x) f (x) g(x).
The domain of the sum and difference functions is the set of all real numbers that
are in both the domain of f and the domain of g.
EXAMPLE 1
If f (x)
9 x
2
and g(x) x 2
, find the rules of the functions f g and
f g and their domains.
SOLUTION We have
( f g)(x) f (x) g(x)
9 x
2
x 2
;
( f g)(x) f (x) g(x)
9 x
2
x 2
.
The domain of f consists of all x such that 9 x
2
0 (so that the square root
will be defined), that is, all x with 3 x 3. Similarly, the domain of g con-
sists of all x such that x 2. The domain of f g and f g consists of all real
numbers in both the domain of f and the domain of g, namely, all x such that
2 x 3. ■
TECHNOLOGY TIP
If you have two functions entered in
the equation memory as y
1
and y
2
,
you can graph their sum by entering
y
1
y
2
as y
3
in the equation memory
and graphing y
3
. Differences, products,
and quotients are graphed similarly.
To find the correct keys for y
1
and y
2
,
see the Tip on page 153.
