Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

DOMAINS
When the rule of a function is given by a formula, as in Examples 3–7, its domain
(set of inputs) is determined by the following convention.
Thus, the domain of a polynomial function such as f (x) x
3
4x 1 is the
set of all real numbers, since f (x) is defined for every value of x. In cases in which
applying the rule of a function leads to division by zero or to the square root of a
negative number, however, the domain may not consist of all real numbers, as
illustrated in the next example.
EXAMPLE 8
Find the domain of the function given by
(a) k(x)
x
x
2
1
5
(b) f (u) u 2
SOLUTION
(a) When x 1, the denominator of
x
x
2
1
5
is 0, and the fraction is not defined.
When x 1, however, the denominator is nonzero and the fraction is defined.
Therefore, the domain of the function k consists of all real numbers except 1.
(b) Since negative numbers do not have real square roots, u 2
is a real num-
ber only when u 2 0, that is, when u 2. Therefore, the domain of f
consists of all real numbers greater than or equal to 2, that is, the interval
[2, ). ■
EXAMPLE 9
A piecewise-defined function is one whose rule includes several formulas, such
as
2x 3ifx 4
f(x)
x
2
1if4 x 10.
Find each of the following.
(a) f (5) (b) f (8) (c) f (k) (d) The domain of f.
SOLUTION
(a) Since 5 4, the first part of the rule applies:
f (5) 2(5) 3 7.
(b) Since 8 is between 4 and 10, the second part of the rule applies:
f (8) 8
2
1 63.
156 CHAPTER 3 Functions and Graphs
Domain
Convention
Unless specific information to the contrary is given, the domain of a func-
tion f includes every real number (input) for which the rule of the function
produces a real number as output.
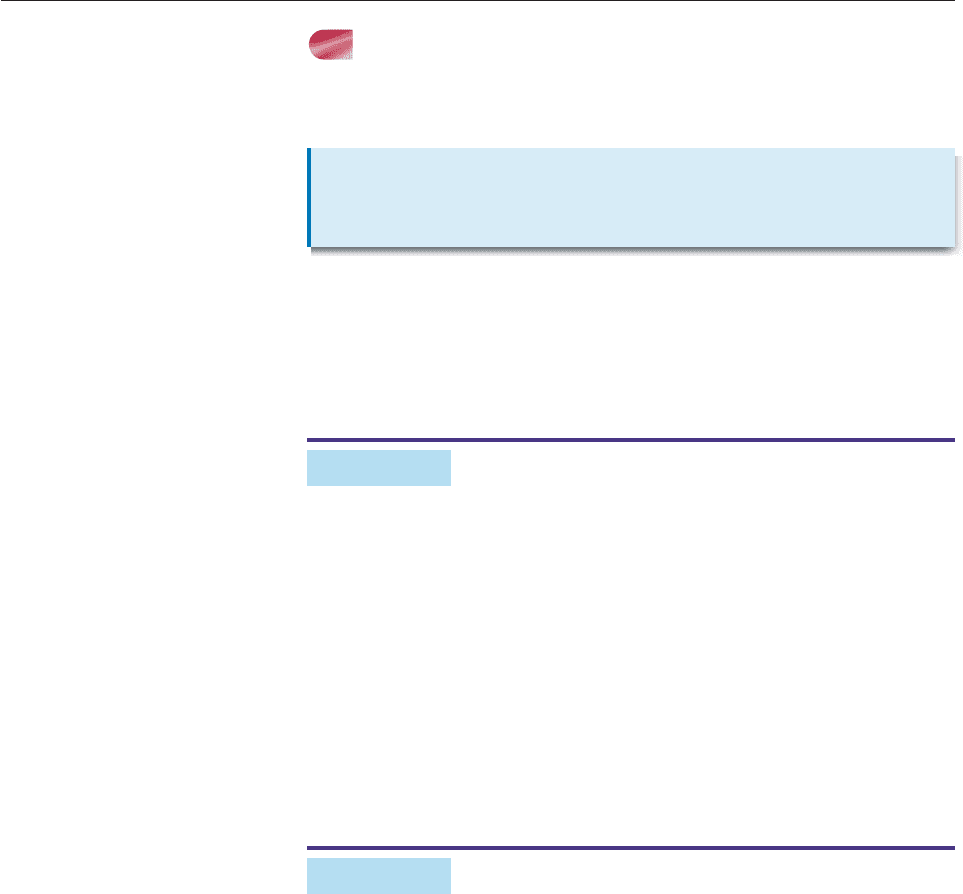
(c) We cannot find f (k) unless we know whether k 4 or 4 k 10.
(d) The rule of f gives no directions when x 10, so the domain of f consists of
all real numbers x with x 10, that is, (, 10]. ■
EXAMPLE 10
Use Example 1 to write the rule of the piecewise-defined function T that gives the
Louisiana state income tax T(x) on an income of x dollars.
SOLUTION By translating the information in the table in Example 1 into func-
tional notation, we obtain
.021x if 0 x 12,500
T(x)
262.50 .0345(x 12,500) if 12,500 x 25,000
693.75 .048(x 25,000) if x 25,000. ■
APPLICATIONS
The domain convention does not always apply when dealing with applications.
Consider, for example, the distance function for falling objects, d(t) 16t
2
(see
Example 2). Since t represents time, only nonnegative values of t make sense
here, even though the rule of the function is defined for all values of t.
A real-life situation may lead to a function whose domain
is smaller than the one dictated by the domain convention.
EXAMPLE 11
A glassware factory has fixed expenses (mortgage, taxes, machinery, etc.) of
$12,000 per week. It costs 80 cents to make one cup (labor, materials, shipping).
A cup sells for $1.95. At most 18,000 cups can be manufactured and sold each
week.
(a) Express the weekly revenue as a function of the number x of cups made.
(b) Express the weekly costs as a function of x.
(c) Find the domain and the rule of the weekly profit function.
SOLUTION
(a) If R(x) is the weekly revenue from selling x cups, then
R(x) (price per cup) (number sold)
R(x) 1.95x.
(b) If C(x) is the weekly cost of manufacturing x cups, then
C(x) (cost per cup) (number sold) (fixed expenses)
C(x) .80x 12,000.
SECTION 3.2 Functional Notation 157

(c) If P(x) is the weekly profit from selling x cups, then
P(x) Revenue Cost
P(x) R(x) C(x)
P(x) 1.95x (.80x 12,000) 1.95x .80x 12,000
P(x) 1.15x 12,000.
Although this rule is defined for all real numbers x, the domain of the func-
tion P consists of the possible number of cups that can be made each week.
Since you can make only whole cups and the maximum production is 18,000,
the domain of P consists of all integers from 0 to 18,000. ■
EXAMPLE 12
Let P be the profit function in Example 11.
(a) What is the profit from selling 5000 cups? From 14,000 cups?
(b) What is the break-even point?
SOLUTION
(a) We evaluate the function P(x) 1.15x 12,000 at the required values of x:
P(5000) 1.15(5000) 12,000 $6250
P(14,000) 1.15(14,000) 12,000 $4100.
Thus, sales of 5000 cups produce a loss of $6250, while sales of 14,000 pro-
duce a profit of $4100.
(b) The break-even point occurs when revenue equals costs (that is, when profit
is 0). So we set P(x) 0 and solve for x:
1.15x 12,000 0
1.15x 12,000
x
12
1
,
.
0
1
0
5
0
10,434.78.
Thus, the break-even point occurs between 10,434 and 10,435 cups. There is
a slight loss from selling 10,434 cups and a slight profit from selling 10,435.
■
158 CHAPTER 3 Functions and Graphs
EXERCISES 3.2
In Exercises 1 and 2, find the indicated values of the function
by hand and by using the table feature of a calculator (or the
EVAL key on TI-85/86). If your answers do not agree with
each other or with those at the back of the book, you are either
making algebraic mistakes or incorrectly entering the function
in the equation memory.
1. f (x)
x
x
2
3
4
(a) f (1) (b) f (0) (c) f (1) (d) f (2) (e) f (3)
2. g(x) x 4
2
(a) g(2) (b) g(0) (c) g(4) (d) g(5) (e ) g(12)
Exercises 3–24 refer to these three functions:
f (x) x 3
x 1
g(t) t
2
1
h(x) x
2
1
x
2.
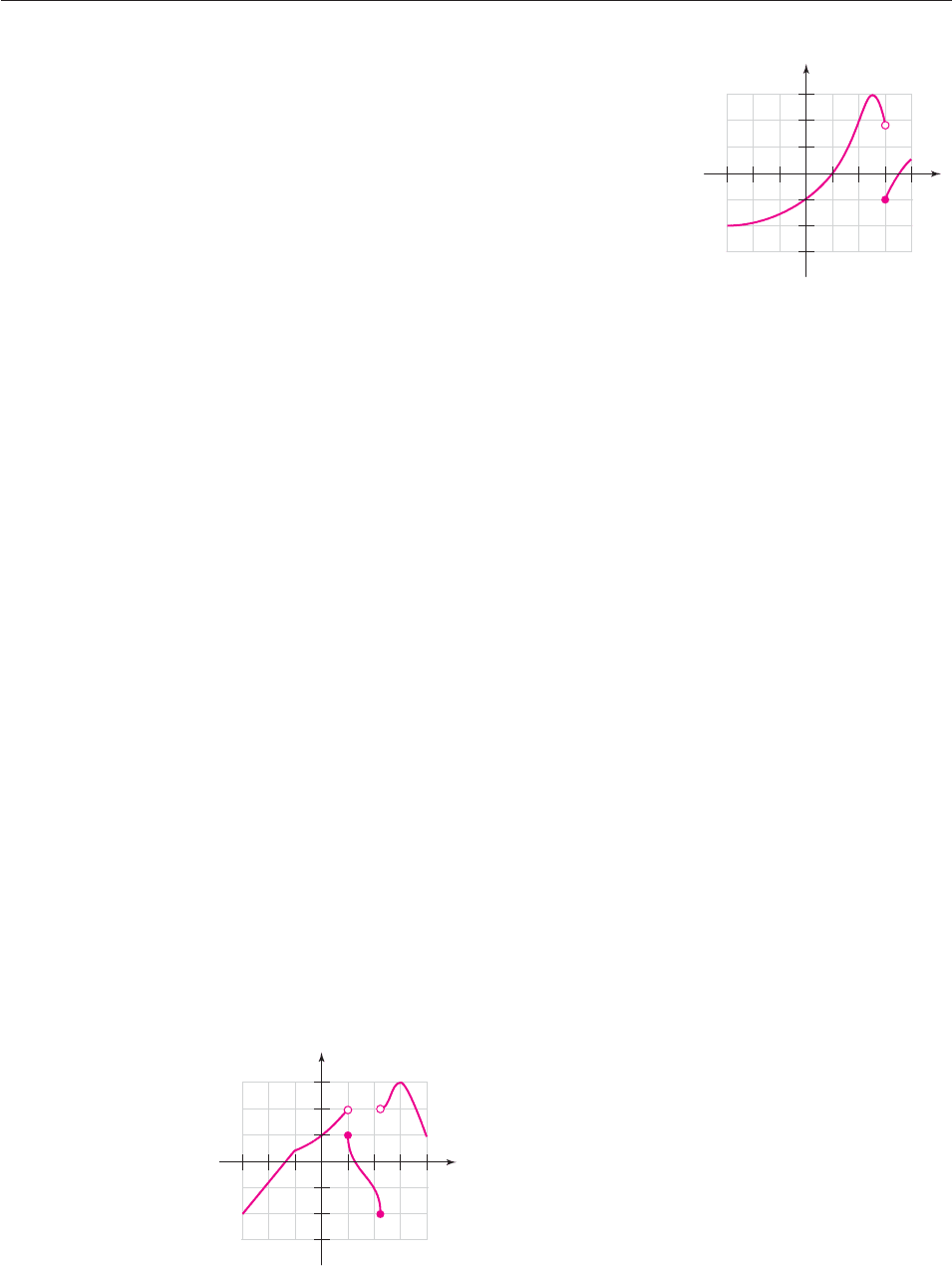
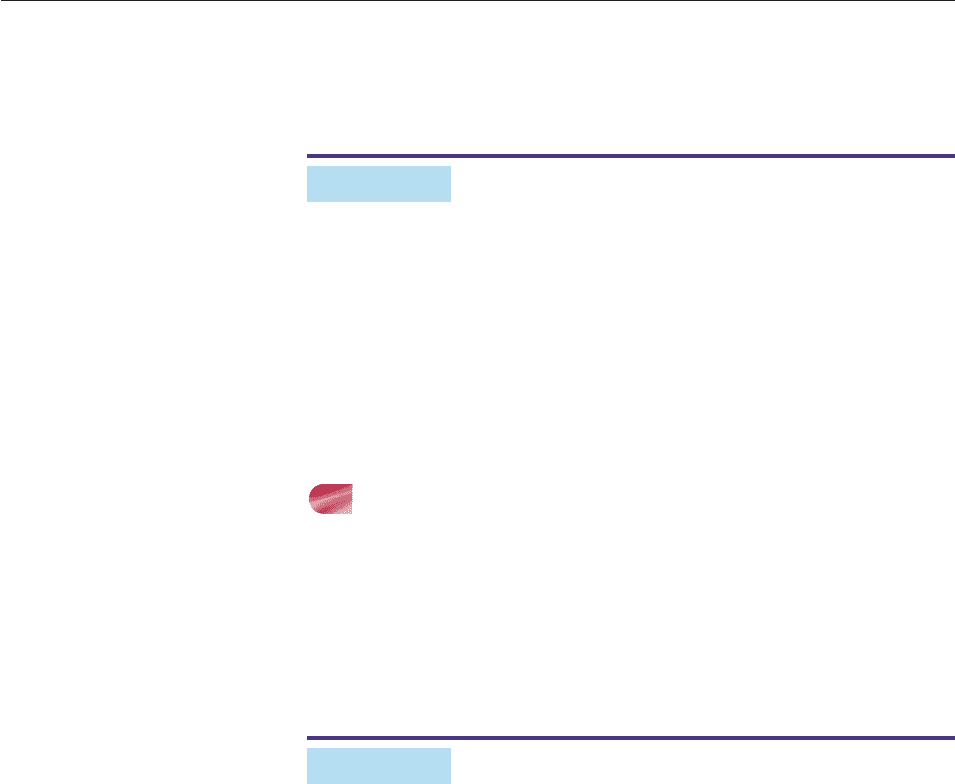
In each case, find the indicated value of the function.
3. f (0) 4. f (1)
5. f (2
) 6. f (2
1)
7. f (2) 8. f (3/2)
9. h(4) 10. h(3/2)
11. h(p 1) 12. h(m)
13. h(a k) 14. f (a)
15. h(x) 16. h(2 x)
17. h(x 3) 18. g(3)
19. g(s 1) 20. g(1 r)
21. g(t) 22. g(t h)
23. f(g(3)) 24. f(g(t))
In Exercises 25–34, assume h 0. Compute and simplify the
difference quotient
f(x h
h
) f(x)
25. f (x) x 1 26. f (x) 10x
27. f (x) 3x 7 28. f (x) x
2
29. f (x) x x
2
30. f (x) x
3
31. f (x) x
32. f (x) 1/x
33. f (x) x
2
3 34. f (x) 3
35. In each part, compute f (a), f (b), and f (a b), and deter-
mine whether the statement “f (a b) f (a) f (b)” is true
or false for the given function.
(a) f (x) x
2
(b) f (x) 3x (c) f (x) 5
36. In each part, compute g(a), g(b), and g(ab), and determine
whether the satement “g(ab) g(a)
g(b)” is true or false
for the given function.
(a) g(x) x
3
(b) g(x) 5x (c) g(x) 2
37. If f (x) x
3
cx
2
4x 1 for some constant c and
f (1) 2, find c. [Hint: Use the rule of f to compute f (1).]
38. If f (x)
d
x
x
3
5
and f (4) 3, find d.
39. The rule of the function f is given by the graph, as in Exam-
ple 4 of Section 3.1. Find
(a) The domain of f
(b) The range of f
(c) f (3)
(d) f (1)
(e) f (1)
(f) f (2)
40. The rule of the function g is given by the graph. Find
(a) The domain of g
(b) The range of g
(c) g(3)
(d) g(1)
(e) g(1)
(f) g(4)
x if x 2
41. Let f (x)
x if x 0
This function is identical to a function you already know.
What is that function?
1x if x 0
42. Let f (x)
2ifx 0
Find the domain of f.
x
2
2x if x 2
43. If f (x)
find
3x 5if2 x 20
(a) The domain of f
(b) f (3) (c) f (1) (d) f (2) (e) f (7/3)
2x 3ifx 1
44. If g(x)
x 5if1 x 2 find
x
2
if x 2
(a) The domain of g
(b) g(2.5) (c) g(1) (d) g(2) (e) g(4)
In Exercises 45–58, determine the domain of the function
according to the usual convention.
45. f(x) x
2
46. g(x)
x
1
2
2
47. h(t) t 1 48. k(u) u
49. k(x) x x
1 50. h(x)
(x 1
)
2
51. g(u)
u
u
52. h(x)
x
2
x
1
1
53. g( y) y 54. f (t) t
55. g(u)
u
2
u
2
u
1
6
56. f(t)
4 t
2
57. f(x)
9 (x
9)
2
58. f(x) x
x
2
1
59. Give an example of two different functions f and g that have
all of the following properties:
f (1) 1 g(1) and f (0) 0 g(0)
and f (1) 1 g(1).
SECTION 3.2 Functional Notation 159
1
−1
−2
−3
−2−3
2
3
3421
x
y
−1
1
−1
−2
−3
−2−3
2
3
421
x
y
−1
3
60. Give an example of a function g with the property that
g(x) g(x) for every real number x.
61. Give an example of a function g with the property that
g(x) g(x) for every real number x.
In Exercises 62–65, find the values of x for which f(x) g(x).
62. f (x) 2x
2
4x 4; g(x) x
2
12x 6
63. f (x) 2x
2
13x 14; g(x) 8x 2
64. f (x) 3x
2
x 5; g(x) x
2
2x 26
65. f (x) 2x
2
x 1; g(x) x
2
4x 4
In Exercises 66–68, the rule of a function f is given. Write an
algebraic formula for f(x).
66. Triple the input, subtract 8, and take the square root of the
result.
67. Square the input, multiply by 3, and subtract the result
from 8.
68. Cube the input, add 6, and divide the result by 5.
69. A potato chip factory has a daily overhead from salaries
and building costs of $1800. The cost of ingredients
and packaging to produce a pound of potato chips is 50¢.
A pound of potato chips sells for $1.20. Show that the fac-
tory’s daily profit is a function of the number of pounds
of potato chips sold, and find the rule of this function.
(Assume that the factory sells all the potato chips it produces
each day.)
70. Jack and Jill are salespersons in the suit department of a
clothing store. Jack is paid $200 per week plus $5 for each
suit he sells, whereas Jill is paid $10 for every suit she
sells.
(a) Let f (x) denote Jack’s weekly income, and let g(x)
denote Jill’s weekly income from selling x suits. Find
the rules of the functions f and g.
(b) Use algebra or a table to find f (20) and g(20), f (35) and
g(35), f (50) and g(50).
(c) If Jack sells 50 suits a week, how many must Jill sell to
have the same income as Jack?
71. A person who needs crutches can determine the correct
length as follows: a 50-inch-tall person needs a 38-inch-
long crutch. For each additional inch in the person’s height,
add .72 inch to the crutch length.
(a) If a person is y inches taller than 50 inches, write an
expression for the proper crutch length.
(b) Write the rule of a function f such that f (x) is the
proper crutch length (in inches) for a person who is
x inches tall. [Hint: Replace y in your answer to
part (a) with an expression in x. How are x and y
related?]
72. The table shows the 2006 federal income tax rates for a
single person.
160 CHAPTER 3 Functions and Graphs
(a) Write the rule of a piecewise-defined function T such
that T(x) is the tax due on a taxable income of x dollars.
(b) Find T(24,000), T(35,000), and T(200,000).
73. Suppose a car travels at a constant rate of 55 mph for
2 hours and travels at 45 mph thereafter. Show that distance
traveled is a function of time, and find the rule of the
function.
74. A man walks for 45 minutes at a rate of 3 mph, then jogs for
75 minutes at a rate of 5 mph, then sits and rests for
30 minutes, and finally walks for 1
1
2
hours. Find the rule of
the function that expresses his distance traveled as a func-
tion of time. [Caution: Don’t mix up the units of time; use
either minutes or hours, not both.]
75. Suppose that the width and height of the box in the figure
are equal and that the sum of the length and the girth is 108
(the maximum size allowed by the post office).
(a) Express the length y as a function of the width x.
[Hint: Use the girth.]
(b) Express the volume V of the box as a function of the
width x. [Hint: Find a formula for the volume and use
part (a).]
76. A rectangular region of 6000 square feet is to be fenced in
on three sides with fencing costing $3.75 per foot and on the
fourth side with fencing costing $2.00 per foot. Express the
cost of the fence as a function of the length x of the fourth
side.
Girth
Length
Width
Height
Taxable Income
Over But Not Over Tax
0 $7,300 10% of income
$7,300 $29,700 $730.00 15% of amount
over $7,300
$29,700 $71,950 $4090.00 25% of amount
over $29,700
$71,950 $150,150 $14,652.50 28% of
amount over $71,950
$150,150 $326,450 $36,548.50 33% of
amount over $150,150
$326,450 $94,727.50 35% of
amount over $326,450
77. A box with a square base measuring t t ft is to be made of
three kinds of wood. The cost of the wood for the base is
85¢ per square foot; the wood for the sides costs 50¢ per
square foot, and the wood for the top $1.15 per square foot.
The volume of the box is to be 10 cubic feet. Express the
total cost of the box as a function of the length t.
78. Average tuition and fees in private four-year colleges in
recent years were as follows.*
(a) Use linear regression to find the rule of a function f that
gives the approximate average tuition in year x, where
x 0 corresponds to 1990.
t
t
SECTION 3.3 Graphs of Functions 161
(b) Find f (6), f (8), and f (10). How do they compare with
the actual figures?
(c) Use f to estimate tuition and fees in 2011.
79. The number of U.S. commercial radio stations whose pri-
mary format is top 40 hits has been increasing in recent
years, as shown in the table.*
(a) Use linear regression to find the rule of a function g
that gives the number of top-40 stations in year x, where
x 0 corresponds to 1990.
(b) Find g(8) and g(11). How do they compare with the
actual figures?
(c) Data for the year 2000 is missing. Estimate the number
of stations in 2000.
(d) Assuming that this function remains accurate, estimate
the number of stations in 2011.
Tuition
Year and Fees
1995 $12,432
1996 $12,823
1997 $13,664
1998 $14,709
Tuition
Year and Fees
1999 $15,380
2000 $16,332
2001 $17,727
2002 $18,723
Number of
Year Stations
1998 379
1999 401
2001 468
2002 474
2003 491
2004 497
2005 502
*The College Board. *World Almanac and Book of Facts 2006.
3.3 Graphs of Functions
■ Recognize the general shape and behavior of graphs of basic
functions.
■ Graph step functions and piecewise-defined functions.
■ Find local maxima and minima.
■ Determine intervals on which a function is increasing or
decreasing.
■ Use the vertical line test to identify the graph of a
function.
■ Interpret information presented in a graph.
The graph of a function f is the graph of the equation y f (x). Hence
The graph of the function f consists of the points (x, f (x))
for every number x in the domain of f.
When the rule of a function is given by an algebraic formula, the graph is easily
obtained with technology. However, machine-generated graphs can sometimes be
Section Objectives
incomplete or misleading. So the emphasis here is on using your algebraic knowl-
edge before reaching for a calculator. Doing so will often tell you that a calculator
is inappropriate or help you to interpret screen images when a calculator is used.
Some functions appear so frequently that you should memorize the shapes of
their graphs, which are easily obtained by hand-graphing or by using technology.
Regardless of how you first find these graphs, you should be able to reproduce them
without looking them up or resorting to technology. These basic graphs are summa-
rized in the catalog of functions at the end of this section. A title on an example
(such as “linear function” in Example 1) indicates a function that is in the catalog.
EXAMPLE 1
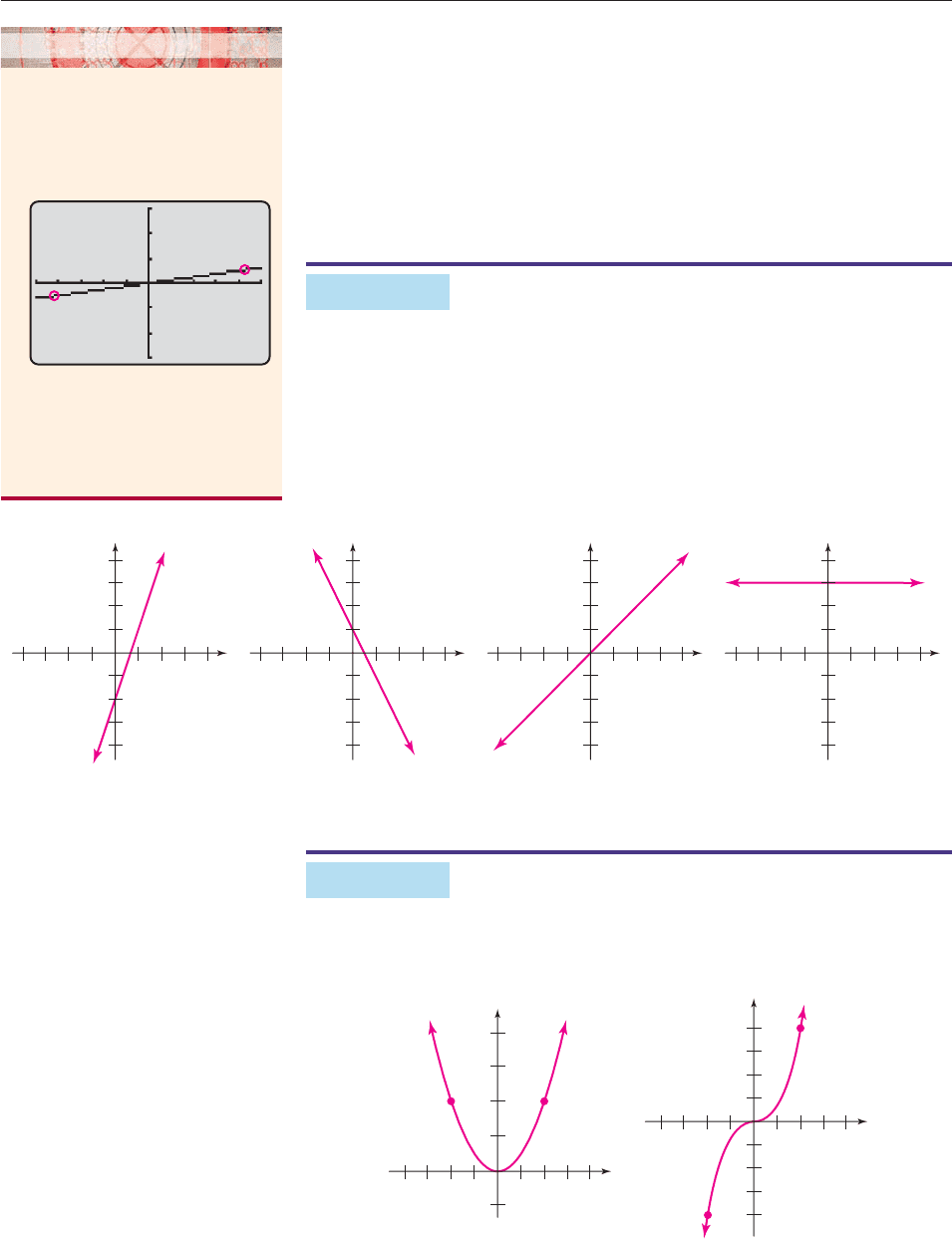
Linear Functions The graph of a function of the form
f (x) mx b (with m and b constants)
is the graph of the equation y mx b. As we saw in Section 1.4, the graph is a
straight line with slope m and y-intercept b that can easily be obtained by hand.
Some typical linear functions are graphed in Figure 3–8 (several of them have
special names). ■
Figure 3–8
EXAMPLE 2
Square and Cube Functions Figure 3–9 shows the graphs of f (x) x
2
and
g(x) x
3
. They can be obtained by plotting points (as was done for f in Example 1
of Section 2.1) or by using technology. ■
Figure 3–9
−6
−8
2
f(x) = x
2
143
−2 −1−3−4
−2
2
4
6
8
x
y
2
(2, 4)(−2, 4)
(2, 8)
(−2, −8)
g(x) = x
3
143
−2 −1−3−4
−2
−4
2
4
6
8
x
y
2
f(x) = 3x − 2
143
−2−3−4
−2
−1
1
2
3
4
−3
−4
x
y
2
f(x) = −2x + 1
143
−2−3−4
−2
−1
1
2
3
4
−3
−4
x
y
2
f(x) = x
143
−2−3−4
−2
−1
1
2
3
4
−3
−4
x
y
2
f(x) = 3
143
−2−3−4
−2
−1
1
2
3
4
−3
−4
x
y
Identity Function Constant Function
162 CHAPTER 3 Functions and Graphs
CAUTION
Due to the resolution of your calculator’s
screen, its graphs will suffer from
pixellation. For example, it may graph
y
1
8
x like so:
In reality, nothing special is happening
at the indicated points, it just happens
that a calculator can’t draw a smooth,
straight line with that shape.
3
5
5
3

EXAMPLE 3
Square Root Function The graph of f (x) x
in Figure 3–10 is easily found.
Why does it lie entirely in the first quadrant? ■
STEP FUNCTIONS
The greatest integer function f (x) x was introduced in Example 7 of
Section 3.1. It can easily be graphed by hand, as in the next example.
EXAMPLE 4
Greatest Integer Function We graph f (x) x by considering the values of
the function between each two consecutive integers. For instance,
Thus, between x 2 and x 1, the value of f (x) x is always 2, so the
graph there is a horizontal line segment, all of whose points have second coordi-
nate 2. The rest of the graph is obtained similarly (Figure 3–11). An open circle
in Figure 3–11 indicates that the endpoint of the segment is not on the graph,
whereas a closed circle indicates that the endpoint is on the graph. ■
A function whose graph consists of horizontal line segments, such as
Figure 3–11, is called a step function. Graphing step functions with reasonable
accuracy on a calculator requires some care. Even then, some features of the
graph might not be shown.
EXAMPLE 5
As of this writing, United States postage rates for large envelopes are 80 cents
for the first ounce (or fraction thereof) plus 17 cents for each additional ounce
or fraction thereof. Verify that the postage P(x) for a letter weighing x ounces is
given by P(x) .80 .171 x. For instance, the postage for a 2.5 ounce
large envelope is
P(2.5) .80 .171 2.5 .80 .17(2) 1.14
Although the rule of P makes sense for all real numbers, the domain of the func-
tion consists of positive numbers (why?). The graph of P is in Figure 3–12. ■
SECTION 3.3 Graphs of Functions 163
4
f(x) = x
286
1
2
3
4
x
y
Figure 3–10
x 2 x 1 1 x 00 x 11 x 22 x 3
x 2 1012
2
2
13
3
4
1
−2 −1−3
−2
−1
−4
−3
x
y
Figure 3–11
Graph the greatest integer function f (x) x on your calculator (see the Technol-
ogy Tip on page 145). Does your graph look like Figure 3–11, or does it include
vertical segments? Now change the graphing mode of your calculator to “dot” rather
than “connected”, and graph again. How does this graph compare with Figure 3–11?
Can you tell from the graph which endpoints are included and which are excluded?
GRAPHING EXPLORATION
214365
0.80
1.14
1.48
1.82
x
y
Figure 3–12

PIECEWISE-DEFINED FUNCTIONS
Piecewise-defined functions were introduced in Example 9 of Section 3.2. Graph-
ing them correctly requires some care.
EXAMPLE 6
The graph of the piecewise-defined function
x
2
if x 1
f(x)
x 2 if 1 x 4
is made up of parts of two graphs, corresponding to the different parts of the rule
of the function:
x 1 For these values of x, the graph of f coincides with the graph of
y x
2
, which was sketched in Figure 3–9.
1 x 4 For these values of x, the graph of f coincides with the graph of
y x 2, which is a straight line.
Therefore, we must graph
y x
2
when x 1 and y x 2 when 1 x 4.
Combining these partial graphs produces the graph of f in Figure 3–13. ■
Piecewise-defined functions can be graphed on a calculator, provided that you use
the correct syntax. Once again, however, the screen does not show which end-
points are included or excluded from the graph.
164 CHAPTER 3 Functions and Graphs
Use the Technology Tip in the margin and the directions here to graph the function f
of Example 6 on a calculator. On TI-84/86 and HP-39gs, graph these two equa-
tions on the same screen:
y
1
(x
x
2
1)
y
2
(x
(x
1
)(x
2
)
4)
.
On TI-89, graph the following equations on the same screen (the symbol is on the
keyboard; “and” is in the TESTS submenu of the MATH menu):
y
1
x
2
x 1
y
2
x 2x 1 and x 4.
To graph f on Casio, with the viewing window of Figure 3–13, graph these equations
on the same screen (including commas and square brackets):
y
1
x
2
, [6, 1]
y
2
x 2, [1, 4].
How does your graph compare with Figure 3–13?
GRAPHING EXPLORATION
1
3
6
1
y
x
4
⫺2
Figure 3–13
TECHNOLOGY TIP
Inequality symbols can be found in the
following menu/submenu:
TI-84+/86: TEST
TI-89: MATH/TEST
HP-39gs: MATH/TESTS
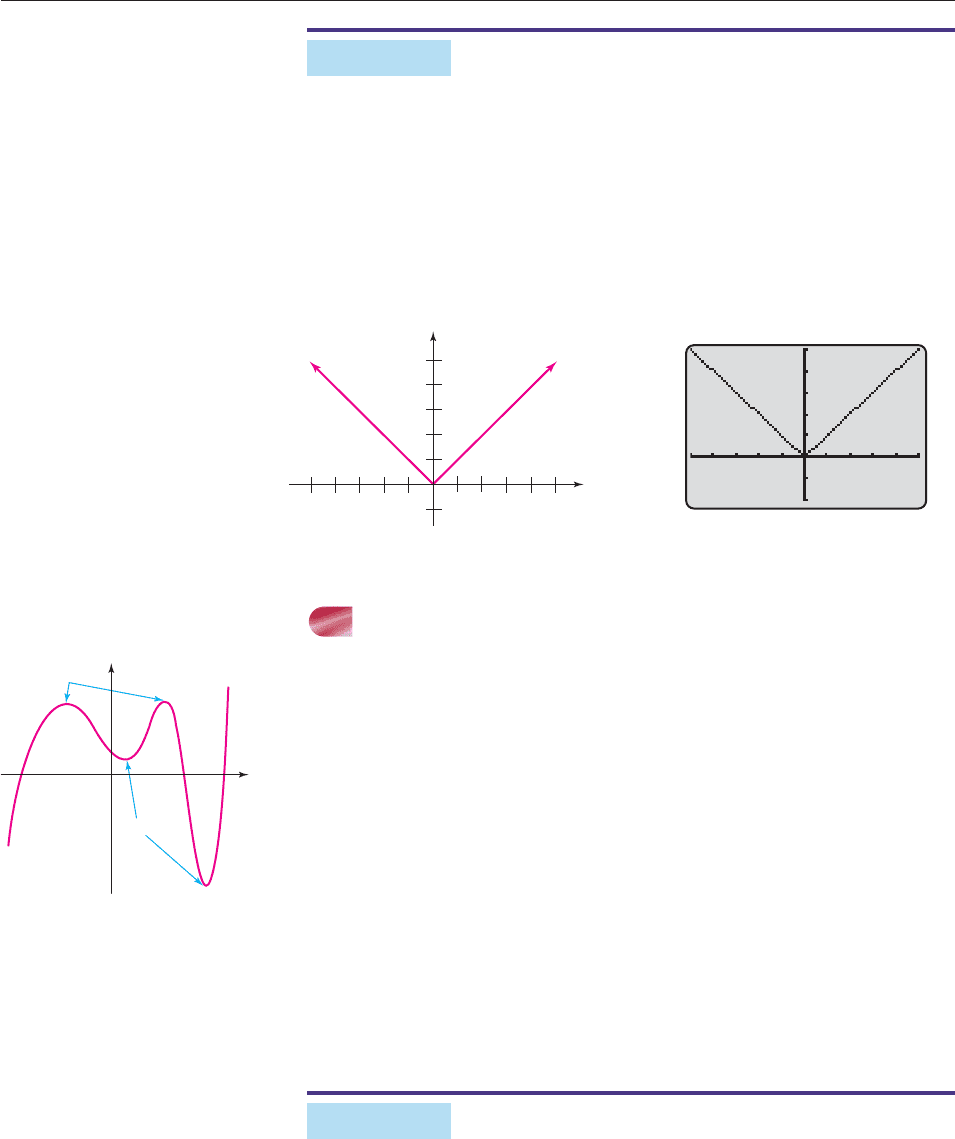
EXAMPLE 7
Absolute Value Function The absolute value function f (x) x is also a
piecewise-defined function, since by definition,
x if x 0
x
x if x 0.
Its graph can be obtained by drawing the part of the line y x to the right of the
origin and the part of the line y x to the left of the origin (Figure 3–14) or by
graphing y ABS x on a calculator (Figure 3–15). ■
Figure 3–14 Figure 3–15
LOCAL MAXIMA AND MINIMA
The graph of a function may include some peaks and valleys (Figure 3–16). A
peak is not necessarily the highest point on the graph, but it is the highest point in
its neighborhood. Similarly, a valley is the lowest point in the neighborhood but
not necessarily the lowest point on the graph.
More formally, we say that a function f has a local maximum at x c if the
graph of f has a peak at the point (c, f (c)). This means that all nearby points
(x, f (x)) have smaller y-coordinates, that is,
f (x) f (c) for all x near c.
Similarly, a function has a local minimum at x d provided that
f (x) f (d) for all x near d.
In other words, the graph of f has a valley at (d, f (d )) because all nearby points
(x, f (x)) have larger y-coordinates.
Calculus is usually needed to find the exact location of local maxima and
minima (the plural forms of maximum and minimum). However, they can be accu-
rately approximated by the maximum finder or minimum finder of a calculator.
EXAMPLE 8
The graph of f (x) x
3
1.8x
2
x 1 in Figure 3–17 on the next page does not
appear to have any local maxima or minima. However, if you use the trace feature to
move along the flat segment to the right of the y-axis, you find that the y-coordinates
increase, then decrease, then increase (try it!). To see what’s really going on, we
change viewing windows (Figure 3–18) and see that the function actually has a
5
5
⫺5
⫺2
1
4
3
2
5
1
0
23
y
x
45
⫺2⫺3 ⫺1
⫺1
⫺5 ⫺4
x
y
Peaks
Valleys
SECTION 3.3 Graphs of Functions 165
Figure 3–16
