Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

176 CHAPTER 3 Functions and Graphs
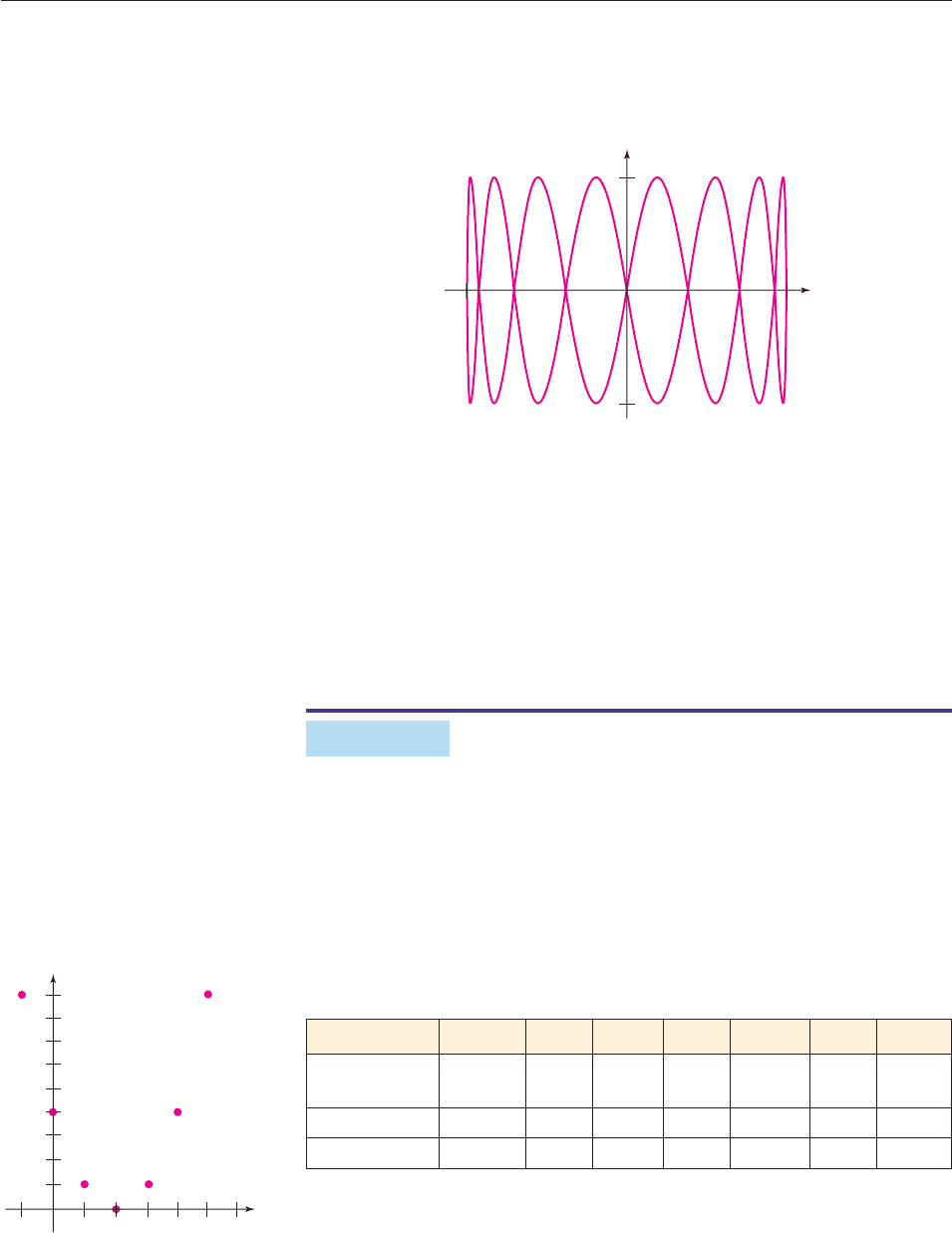
that fail the vertical line test. For example, Figure 3–30 shows a curve (called a
Lissajous Figure) that is important in electrical engineering, yet would be trou-
blesome to describe in functional notation.
Figure 3–30
When we describe a curve by y f(x), we are thinking of the curve as the set of
points satisfying that equation—the set of all the points where the y coordinate is
equal to the value of the function f at the x coordinate. Now we take a different
approach. We picture a point moving on the plane, and let the curve be the path
the point has taken. The equations that describe the coordinates of this point at
a given time t are called parametric equations, and the variable t is called the
parameter.
EXAMPLE 1
Let x
1
2
t 1 and y t
2
.
(a) Make a table of values of x and y for t 3, 2, 1, 0, 1, 2, and 3.
(b) Plot the points in the table.
(c) Connect the points to find the curve traced out by this set of parametric
equations.
SOLUTION
(a)
(b) We plot the points from the final row of the table to obtain Figure 3–31.
(c) We may plot a few more points to see the shape of the curve before we connect
them all. The resultant curve is shown in Figure 3–32.
0
−1
1
1
−1
x
y
t 3 2 10123
x
1
2
t 1 .50.511.522.5
y t
2
9 410149
The point (x, y)(.5, 9) (0, 4) (.5, 1) (1, 0) (1.5, 1) (2, 4) (2.5, 9)
10.50.5 21.5 32.5
2
4
6
8
x
y
Figure 3–31
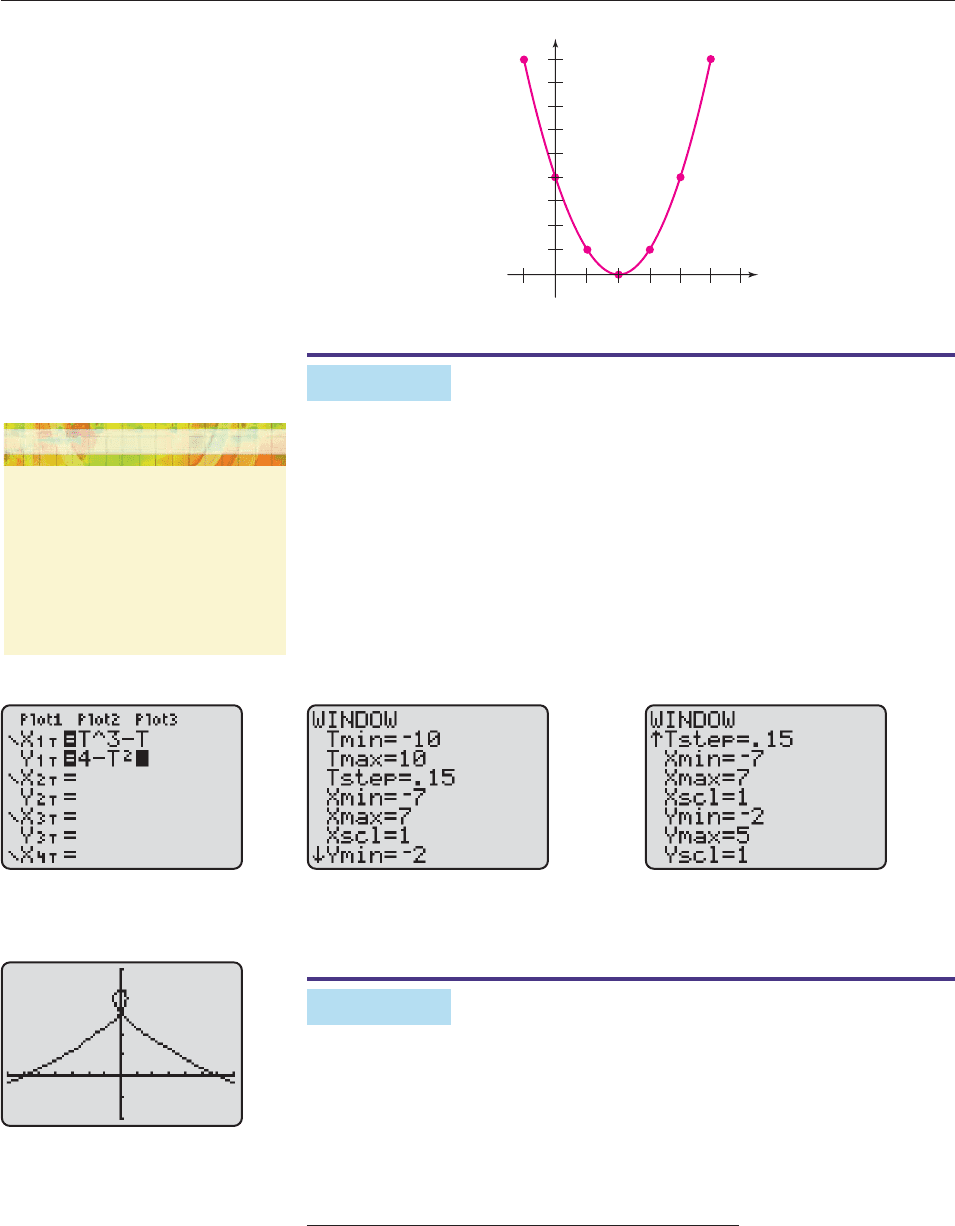
Figure 3–32 ■
EXAMPLE 2
Use a calculator to graph the parametric equations
x t
3
ty 4 t
2
in the window 7 x 7, 2 y 5.
SOLUTION We change to parametric graphing mode, as suggested in the Tech-
nology Tip, and enter the equations (Figure 3–33). Setting up the viewing window
requires some additional steps (first three lines of Figure 3–34). We don’t know a
suitable t-range, so we choose 10 t 10. The t-step (called t-pitch on Casio)
determines how much t changes after a point is plotted; we set it at .15*. Both the
t-range and t-step can be adjusted later if necessary.
Figure 3–33 Figure 3–34 Figure 3–35
Finally, we obtain the graph in Figure 3–36. ■
EXAMPLE 3
Graph the curve given by
x t
2
t 1 and y t
3
4t 6(2 t 3).
SOLUTION Using the standard viewing window, we obtain the graph in Fig-
ure 3–37 on the next page. Note that the graph crosses over itself at one point and
that it does not extend forever to the left and right but has endpoints.
10.50.5 21.5 32.5
2
4
6
8
x
y
SPECIAL TOPICS 3.3.A Parametric Graphing 177
TECHNOLOGY TIP
To change to parametric graphing
mode, select PAR(AMETRIC) in the fol-
lowing menu/submenu:
TI: MODE
Casio: GRAPH/TYPE
HP-39gs: APLET
Figure 3–36
*If the t-step is much smaller than .15, the graph may take a long time to plot. If it is too large, the
graph may look like a series of connected line segments rather than a smooth curve.
As we have seen, when given y as a function of x, we can graph it using the
standard mode on our calculator. When we have x as a function of y, we can graph
the curve using parametric equations.
EXAMPLE 4
Graph x y
3
3y
2
4y 7
SOLUTION Let t be any real number. If y t, then x t
3
3t
2
4t 7.
So the graph of x y
3
3y
2
4y 7 is the same as the graph of the parametric
equations
x t
3
3t
2
4t 7 y t
As before, we change to parametric mode, enter the equations, set up the
viewing window, and graph (Figures 3–38, 3–39). ■
178 CHAPTER 3 Functions and Graphs
TECHNOLOGY TIP
If you have trouble finding appropriate
ranges for t, x, and y, it might help to
use the TABLE feature to display a
table of t-x-y values produced by the
parametric equations.
Graph these same parametric equations, but set the range of t values so that
4 t 4. What happens to the graph? Now change the range of t values so that
10 t 10. Find a viewing window large enough to show the entire graph,
including endpoints.
■
GRAPHING EXPLORATION
10
10
⫺10
⫺10
Figure 3–37
EXERCISES 3.3.A
In Exercises 1–6, find a viewing window that shows a complete
graph of the curve determined by the parametric equations.
1. x 3t
2
5 and y t
2
(4 t 4)
2. The Zorro curve: x .1t
3
.2t
2
2t 4 and
y 1 t (5 t 6)
3. x t
2
3t 2 and y 8 t
3
(4 t 4)
4. x t
2
6t and y t 7
(5 t 9)
5. x 1 t
2
and y t
3
t 1(4 t 4)
6. x t
2
t 1 and y 1 t t
2
In Exercises 7–12, use parametric graphing. Find a viewing
window that shows a complete graph of the equation.
7. x y
3
5y
2
4y 5 8.
3
y
2
y
1
x 2 0
9. xy
2
xy x y
3
2y
2
4
[Hint: First solve for x.]
Figure 3–38
6
10
⫺10
⫺6
Figure 3–39
Any function of the form y f (x) can be expressed in terms of parametric
equations and graphed that way. For instance, to graph f (x) x
2
1, let x t and
y f (x) t
2
1. Parametric graphing will be used hereafter whenever it is con-
venient and will be studied more thoroughly in Section 10.5.

10. 2y xy
2
180x 11. x y
y
2
8 0
12. y
2
x y 5
4 0
THINKERS
13. Graph the curve given by
x (t
2
1)(t
2
4)(t 5) t 3
y (t
2
1)(t
2
4)(t
3
4) t 1
(2.5 t 2.5)
How many times does this curve cross itself?
SECTION 3.4 Graphs and Transformations 179
14. Use parametric equations to describe a curve that crosses
itself more times than the curve in Exercise 13. [Many
correct answers are possible.]
3.4 Graphs and Transformations
■ Recognize the basic geometric transformations of a
graph.
■ Explore the relationship between algebraic changes in the
rule of a function and geometric transformations of its
graph.
If we know the rule of a function, then we can obtain new, related functions by
carefully modifying the rule. In this section, we will explore how certain algebraic
changes to a function’s rule affect its graph. The same format will be used for each
kind of change.
First: You will assemble some evidence by doing a graphing exploration on
your calculator.
Second: We will draw some general conclusions from the evidence you
obtained.
Third: We may discuss how these conclusions can be proved.
Section Objectives
Consider the functions
f(x) x
2
g(x) x
2
5 h(x) x
2
7
Graph f in the standard window and look at the graph, then graph g and see how the
5 changed the basic graph. Then graph h and notice the change the 7 made. Now
answer these questions:
Do the graphs of g and h look very similar to the graph of f in shape?
How do their vertical positions differ?
Where would you predict that the graph of k(x) x
2
9 is located relative to
the graph f (x) x
2
, and what is its shape?
Confirm your prediction by graphing k on the same screen as f, g, and h.
GRAPHING EXPLORATION
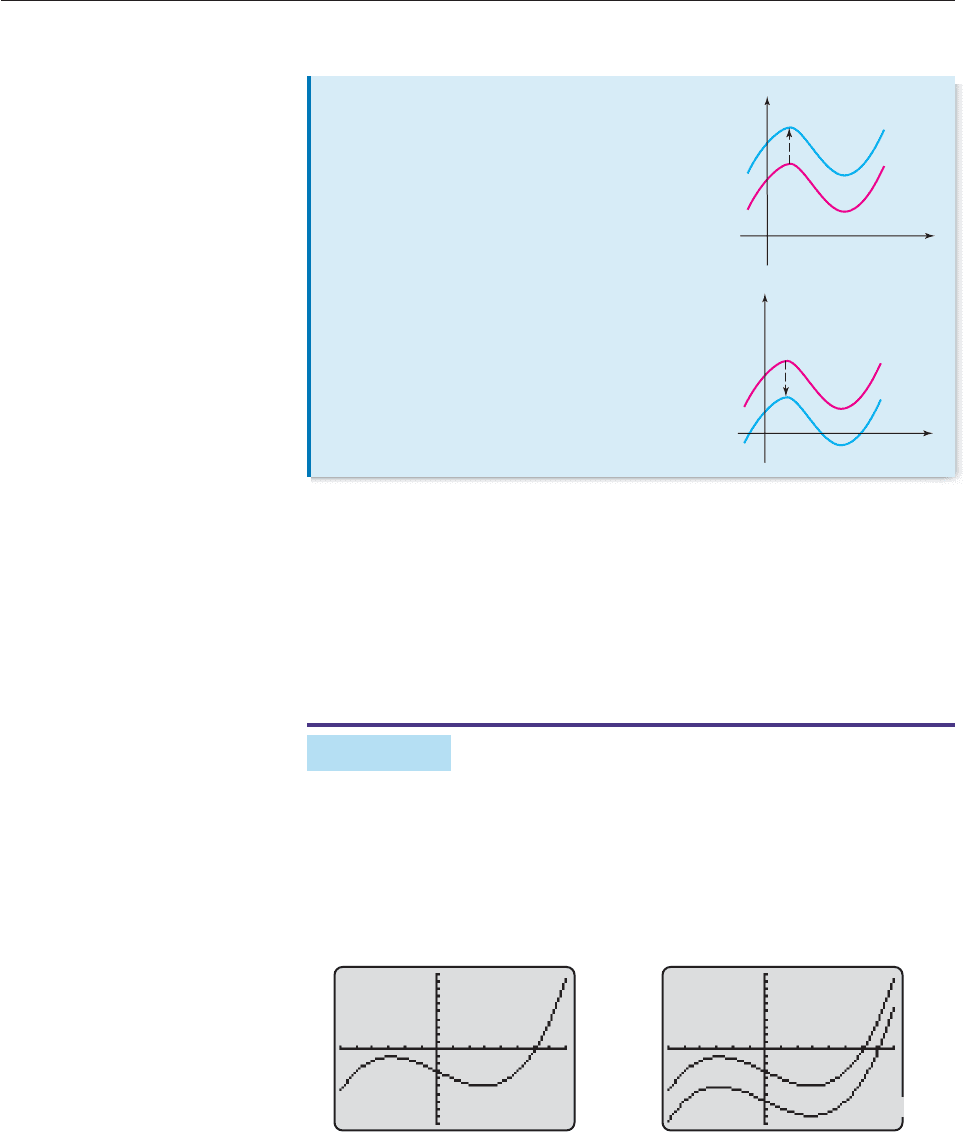
The results of this Exploration should make the following statements plausible.
To see why these statements are true, suppose f (x) x
2
and g(x) x
2
5. For any
given value of x, consider the points
P (x, x
2
) on the graph of f and Q (x, x
2
5) on the graph of g.
The x-coordinates show that P and Q lie in the same vertical line. The y-coordinates
show that Q lies 5 units directly above P. Thus, the graph of g(x) f (x) 5 is just
the graph of f shifted 5 units upward.
EXAMPLE 1
A calculator was used to obtain a graph of f (x) .04x
3
x 3 in Figure 3–40.
The graph of
h(x) f (x) 4 (.04x
3
x 3) 4
is the graph of f shifted 4 units downward, as shown in Figure 3–41.
Figure 3–40 Figure 3–41
Although it may appear that the graph of h is closer to the graph of f at the right
edge of Figure 3–41 than in the center, this is an optical illusion. The vertical dis-
tance between the graphs is always 4 units.
10
8
6
10
f(x)
h(x) f(x) 4
10
8
6
10
F(x)
180 CHAPTER 3 Functions and Graphs
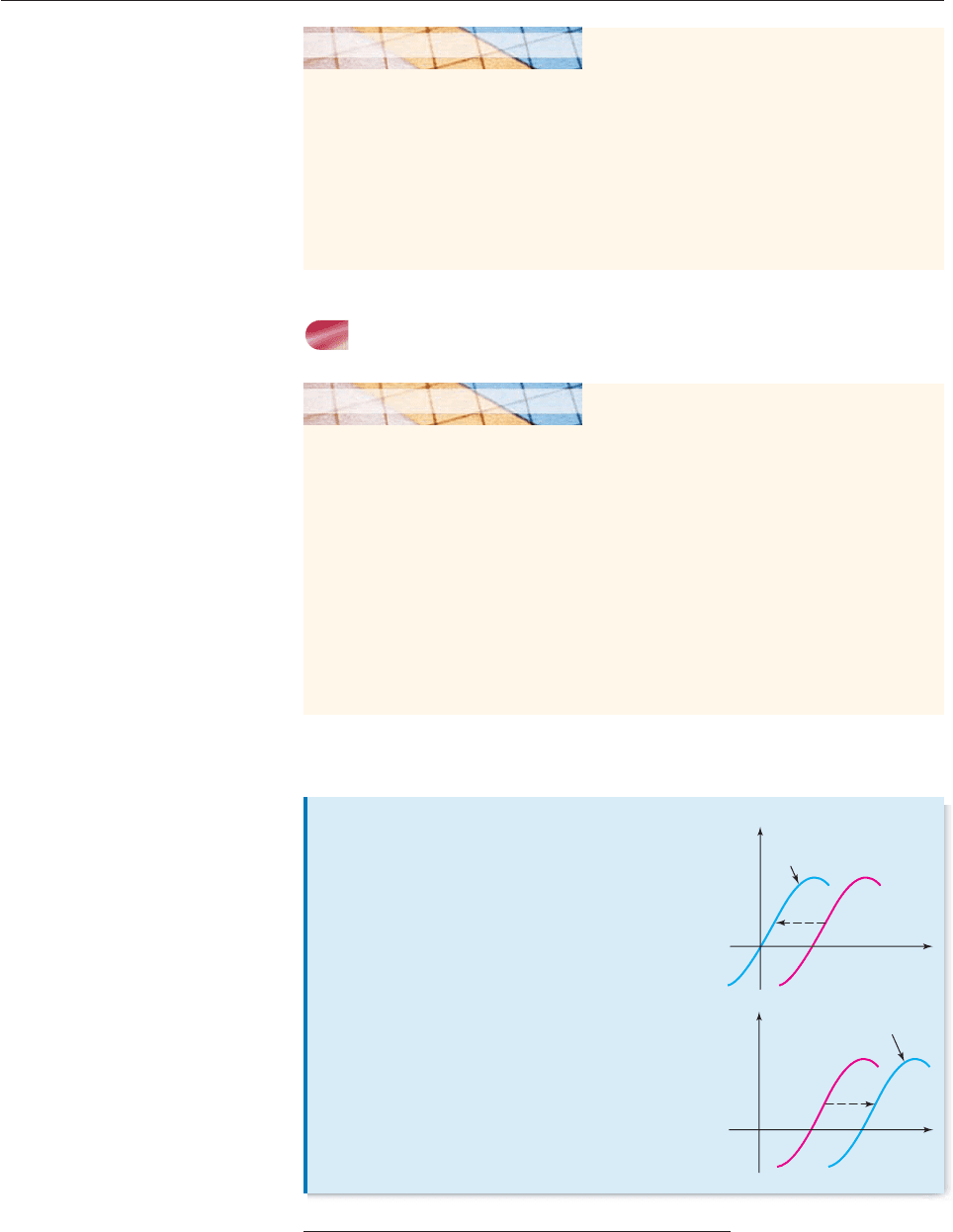
Vertical
Shifts
Let f be a function and c a positive constant.
The graph of g(x) f (x) c is the graph of f
shifted c units upward.
The graph of h(x) f (x) c is the graph of f
shifted c units downward.
x
y
c
f(x)
g(x) = f(x) + c
0
x
y
f(x)
h(x) = f(x) − c
0
c
HORIZONTAL SHIFTS
The results of this Exploration should make the following statements plausible.
SECTION 3.4 Graphs and Transformations 181
Use the trace feature of your calculator as follows to confirm that the vertical dis-
tance is always 4:*
Move the cursor to any point on the graph of f, and note its coordinates.
Use the down arrow to drop the cursor to the graph of h, and note the coordi-
nates of the cursor in its new position.
The x-coordinates will be the same in both cases, and the new y-coordinate will be
4 less than the original y-coordinate.
■
GRAPHING EXPLORATION
Consider the functions
f (x) 2x
3
g(x) 2(x 6)
3
h(x) 2(x 8)
3
Graph f in the standard window and look at the graph, then graph g and see how the
6 changed the basic graph. Then graph h and notice the change the 8 made. Now
answer these questions:
Do the graphs of g and h look very similar to the graph of f in shape?
How do their horizontal positions differ?
Where would you predict that the graph of k(x) 2(x 2)
3
is located relative
to the graph of f (x) 2x
3
, and what is its shape?
Confirm your prediction by graphing k on the same screen as f, g, and h.
GRAPHING EXPLORATION
*The trace cursor can be moved vertically from graph to graph by using the up and down arrows.
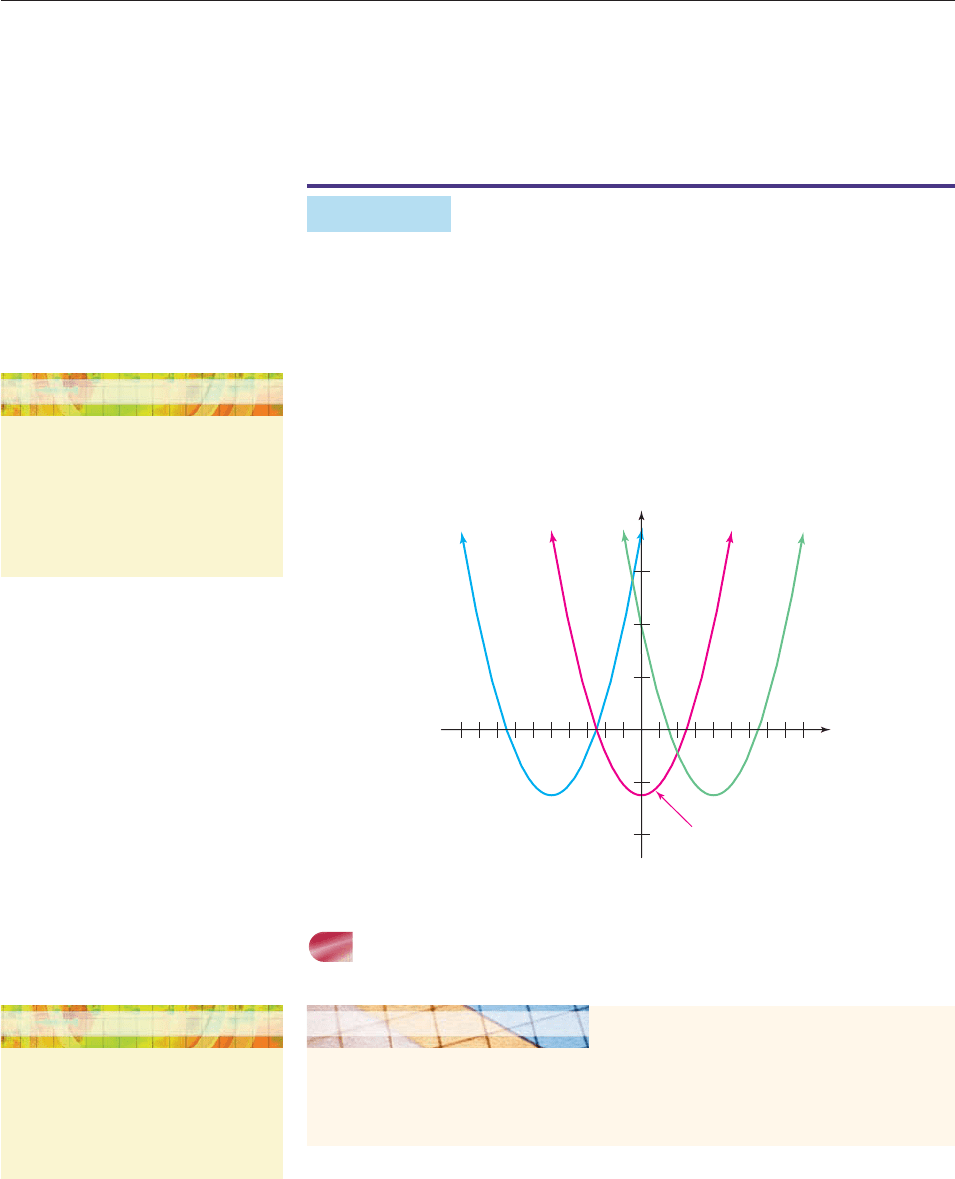
Horizontal
Shifts
Let f be a function and c a positive constant.
The graph of g(x) f (x c) is the graph of f
shifted horizontally c units to the left.
The graph of h(x) f (x c) is the graph of f
shifted horizontally c units to the right.
x
y
f(x)
g(x) = f(x + c)
0
c
c
x
y
f(x)
h(x) = f(x − c)
0
To see why the first statement is true, suppose g(x) f (x 4). Then the value
of g at x is the same as the value of f at x 4, which is 4 units to the right of x on
the horizontal axis. So the graph of f is the graph of g shifted 4 units to the right,
which means that the graph of g is the graph of f shifted 4 units to the left. An anal-
ogous argument works for the second statement in the box.
EXAMPLE 2
In some cases, shifting the graph of a function f horizontally may produce a graph
that overlaps the graph of f. For instance, a graph of f (x) x
2
7 is shown in red
in Figure 3–42. The graph of
g(x) f (x 5) (x 5)
2
7
is the graph of f shifted 5 units to the left, and the graph of
h(x) f (x 4) (x 4)
2
7
is the graph of f shifted 4 units to the right, as shown in Figure 3–42. ■
Figure 3–42
EXPANSIONS AND CONTRACTIONS
The table of values in Figure 3–43 shows that the y-coordinates on the graph of
Y
2
g(x) are always 3 times the y-coordinates of the corresponding points on the
graph of Y
1
f (x). To translate this into visual terms, imagine that the graph of f
is nailed to the x-axis at its intercepts (2). The graph of g is then obtained by
4
g
(x) = f(x + 5)
h(x) = f(x − 4)
f(x) = x
2
− 7
−5
−5
5
10
15
x
y
182 CHAPTER 3 Functions and Graphs
TECHNOLOGY TIP
If the function f of Example 2 is en-
tered as y
1
x
2
7, then the func-
tions g and h can be entered as
y
2
y
1
(x 5) and y
3
y
1
(x 4) on
calculators other than TI-86 and
Casio.
In the viewing window with 5 x 5 and 15 y 15, graph these functions
on the same screen:
f (x) x
2
4 g(x) 3f (x) 3(x
2
4).
GRAPHING EXPLORATION
TECHNOLOGY TIP
On most calculators, you can graph
both functions in the Exploration at the
same time by keying in
y {1, 3}(x
2
4).
“stretching” the graph of f away from the x-axis (with the nails holding the
x-intercepts in place) by a factor of 3, as shown in Figure 3–44.
Figure 3–44
2
3 times as
far from
x-axis
3 times as far
from x-axis
g(x) = 3f(x)
f(x) = x
2
− 4
−2
−5
−10
5
10
15
x
y
SECTION 3.4 Graphs and Transformations 183
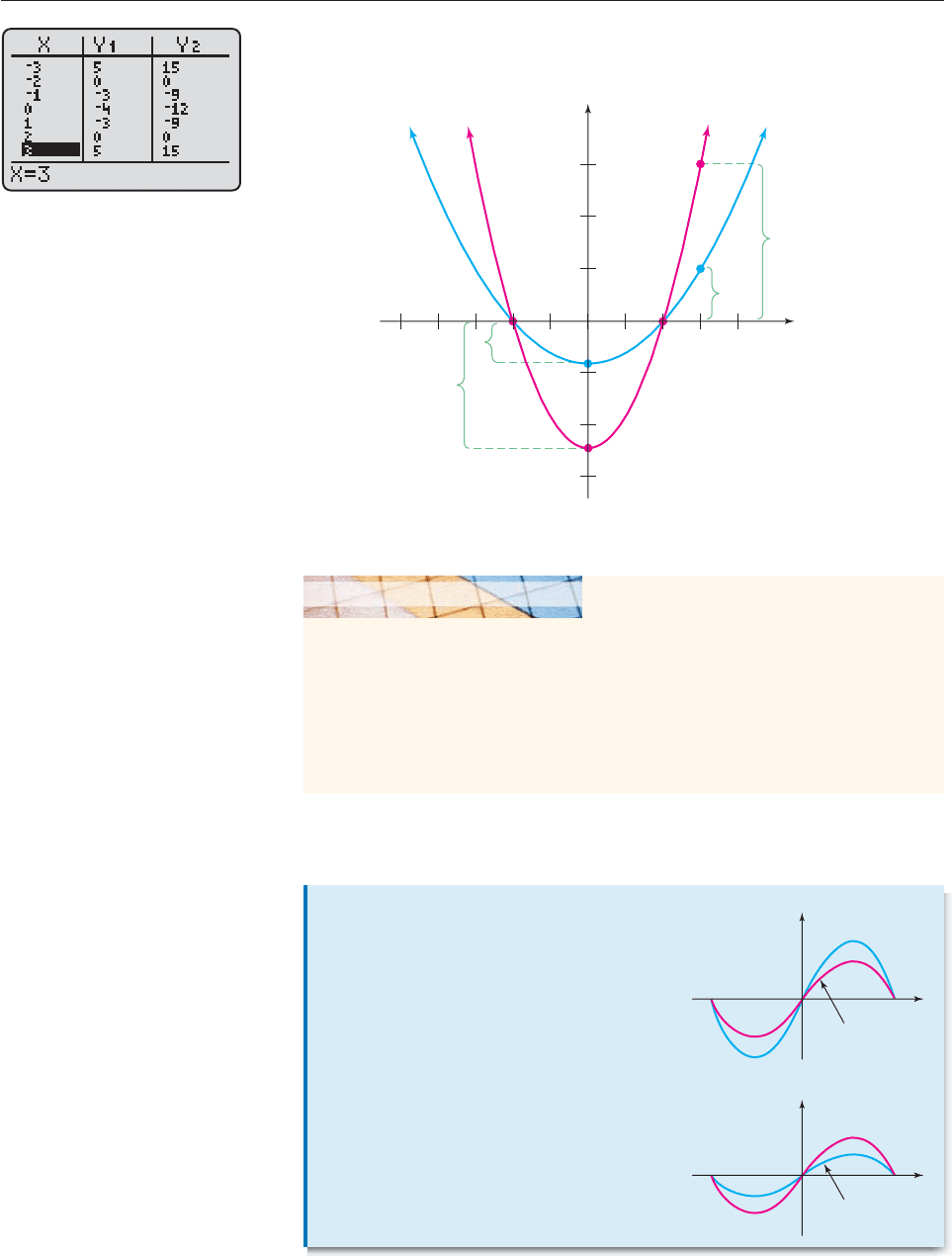
Expansions
and Contractions
If c 1, then the graph of g(x) cf(x) is the
graph of f stretched vertically away from the
x-axis by a factor of c.
If 0 c 1, then the graph of h(x) cf(x)
is the graph of f shrunk vertically toward the
x-axis by a factor of c.
x
y
f(x)
g(x) = cf(x)
0
h(x) = cf(x)
x
y
f(x)
0
Analogous facts are true in the general case.
In the viewing window with 4 x 4 and 5 y 12, graph these functions
on the same screen:
f(x) x
2
4 h(x)
1
4
(x
2
4).
Your screen should suggest that the graph of h is the graph of f “shrunk” vertically
toward the x-axis by a factor of 1/4.
GRAPHING EXPLORATION
Figure 3–43
REFLECTIONS
This Exploration shows that the graph of g is the mirror image (reflection) of the
graph of f, with the x-axis being the mirror. The same thing is true in the general
case.
EXAMPLE 3
If f (x) x
2
3, then the graph of
g(x) f (x) (x
2
3)
is the reflection of the graph of f in the x-axis, as shown in Figure 3–45. ■
184 CHAPTER 3 Functions and Graphs
In the standard viewing window, graph these functions on the same screen.
f (x) .04x
3
xg(x) f (x) (.04x
3
x).
By moving your trace cursor from graph to graph, verify that for every point on the
graph of f, there is a point on the graph of g with the same first coordinate that is on
the opposite side of the x-axis, the same distance from the x-axis.
GRAPHING EXPLORATION
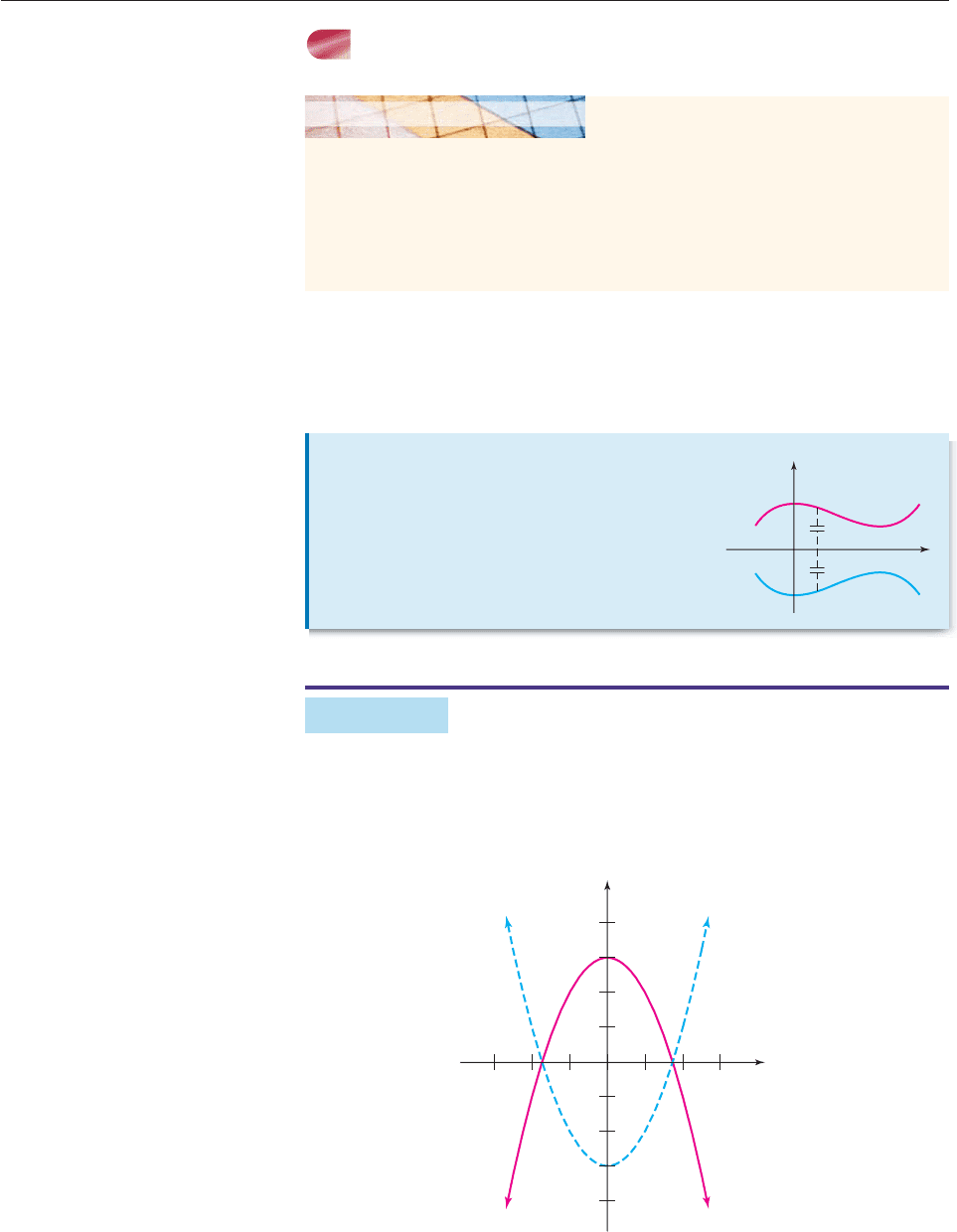
Reflections
Let f be a function. The graph of g(x)
f (x) is the graph of f reflected in the x-axis.
x
y
f(x)
g
(x) = −
f
(x)
0
g(x) = −(x
2
− 3)
f(x) = x
2
− 3
x
y
Figure 3–45

We now examine a different kind of reflection.
This Exploration shows that the graph of h in each case is the mirror image
(reflection) of the graph of f, with the y-axis as the mirror. The same thing is true
in the general case.
To see why this is true, let a be any number. Then
(a, f (a)) is on the graph of f and (a, h(a)) is on the graph of h.
However, h(a) f ((a)) f (a), so the two points are
(a, f (a)) on the graph of f and (a, f (a)) on the graph of h.
These points lie on opposite sides of the y-axis, the same distance from the axis,
because their first coordinates are negatives of each other. The points are on the
same horizontal line because their second coordinates are the same. Thus, every
point on the graph of f has a mirror-image point on the graph of h, the y-axis being
the mirror.
Other algebraic operations and their graphical effects are considered in Exer-
cises 48–61.
COMBINING TRANSFORMATIONS
The transformations described above may be used in sequence to analyze the
graphs of functions whose rules are algebraically complicated.
SECTION 3.4 Graphs and Transformations 185
In the standard viewing window, graph these functions on the same screen:
f (x) 5x 1
0
and h(x) f (x) 5(x)
10
.
Think carefully: How are the two graphs related to the y-axis? Now graph these two
functions on the same screen:
f (x) x
2
3x 3
h(x) f (x) (x)
2
3(x) 3 x
2
3x 3.
Are the graphs of f and h related in the same way as the first pair?
GRAPHING EXPLORATION
Reflections
Let f be a function. The graph of h(x)
f (x) is the graph of f reflected in the y-axis.
x
y
f(x)
h(x) = f(−x)
0
