Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


local maximum and a local minimum (Figure 3–19). The calculator’s minimum
finder shows that the local minimum occurs when x .7633 (Figure 3–20). ■
166 CHAPTER 3 Functions and Graphs
Graph the function in Example 8 in the viewing window of Figure 3–18. Use the
maximum finder to approximate the location of the local maximum.
GRAPHING EXPLORATION
EXAMPLE 9
A box with no top is to be made from a 44 28 inch sheet of cardboard by cut-
ting squares of equal size from each corner and folding up the flaps, as shown in
Figure 3–21.
What size square maximizes the volume of the box?
Figure 3–21
28
44
44 − 2x
xx
x
x
28 − 2x
1.2
1
.2
1.1
Figure 3–19
Figure 3–20
Figure 3–18
10
10
⫺10
⫺10
Figure 3–17

SECTION 3.3 Graphs of Functions 167
SOLUTION The situation here is similar to the one in Example 10 of Sec-
tion 2.3. As that example shows, the function that gives the volume of the box is
V(x) Length Width Height
(44 2x)(28 2x)x
4x
3
144x
2
1232x.
We graph the function and use the maximum finder to determine that the local
maximum occurs when the squares are approximately 5.57 inches on a side
(Figure 3–22). ■
INCREASING AND DECREASING FUNCTIONS
A function is said to be increasing on an interval if its graph always rises as you
move from left to right over the interval. It is decreasing on an interval if its
graph always falls as you move from left to right over the interval. A function is
said to be constant on an interval if its graph is horizontal over the interval.
EXAMPLE 10
Figure 3–23 suggests that f (x) x x 2 is decreasing on the interval (, 0),
increasing on (2, ), and constant on [0, 2]. You can confirm that the function is
actually constant between 0 and 2 by using the trace feature to move along the
graph there (the y-coordinates remain the same, as they should on a horizontal
segment). For an algebraic proof that f is constant on [0, 2], see Exercise 25. ■
Figure 3–22
4000
140
0
Maximum
xc:5.5709
yc:3085.89
CAUTION
A horizontal segment on a calculator graph does not always mean that the function is constant
there. There may be hidden behavior, as was the case in Example 8. When in doubt, either
change the viewing window, or use the trace feature to see if the y-coordinates remain constant
as you move along the “horizontal” segment.
10
6
⫺6
⫺2
Figure 3–23
EXAMPLE 11
On what (approximate) intervals is the function g(x) .5x
3
3x increasing or
decreasing?
SOLUTION The (complete) graph of g in Figure 3–24 shows that g has a local
maximum at P and a local minimum at Q. The maximum and minimum finders
show that the approximate coordinates of P and Q are
P (1.4142, 2.8284) and Q (1.4142, 2.8284).
Therefore, f is increasing on (, 1.4142) and (1.4142, ). It is decreasing on
(1.4142, 1.4142). ■
4
5
⫺5
⫺4
Q
P
Figure 3–24

GRAPH READING
Until now, we have concentrated on translating statements into functional nota-
tion and functional notation into graphs. It is just as important, however, to be able
to translate graphical information into equivalent statements in English or func-
tional notation.
EXAMPLE 12
The entire graph of a function f is shown in Figure 3–25. Find the domain and
range of f.
SOLUTION The graph of f consists of all points of the form (x, f (x)). Thus, the
first coordinates of points on the graph are the inputs (numbers in the domain
of f ) and the second coordinates are the outputs (the numbers in the range of f ).
Figure 3–25 shows that the first coordinates of points on the graph all satisfy
1 x 1, so these numbers are the domain of f. Similarly, the range of f con-
sists of all numbers y such that 0 y p, because these are the second coordi-
nates of points on the graph. ■
EXAMPLE 13
The consumer confidence level reflects people’s feelings about their employment
opportunities and income prospects. Let C(t) be the consumer confidence level at
time t (with t 0 corresponding to 1970) and consider the graph of the function
C in Figure 3–26.*
Figure 3–26
(a) How did the consumer confidence level vary in the 1980s?
(b) What was the lowest level of consumer confidence during the 1990s?
(c) When was the biggest drop in consumer confidence in the 2000s?
(d) During what time periods was the confidence level above 110?
(e) What is the range of C?
SOLUTION
(a) The 1980s correspond to the interval 10 t 20, so we consider the part of
the graph that lies between the vertical lines t 10 and t 20. The second
coordinates of these points range from approximately 60 to 115. So the
5
y
10 15 20 25
100
120
80
60
140
30 35
t
168 CHAPTER 3 Functions and Graphs
1
f(x)
−1
π
x
y
Figure 3–25
*The consumer confidence level is scaled to be 100 in 1985.

consumer confidence level varied from a low of 60 to a high of 115 during
the 1980s.
(b) The 1990s correspond to the interval 20 t 30. Figure 3–26 shows that the
graph has local minimums at t 22 and t 29. The lowest of these three
points is the one at t 22. Hence, the lowest level of consumer confidence in
the 1990s occurred at the beginning of 1992.
(c) The 2000s correspond to the interval 30 t 37. Figure 3–26 shows the
fastest drop occurred between 2001 and 2002.
(d) We must find the values of t for which the graph lies above the horizontal
line through 110. Figure 3–26 shows that this occurs approximately when
17.5 t 19.5 and when 26.5 t 31.5. Thus, the confidence level was
above 110 from the middle of 1987 to the middle of 1989 and from the mid-
dle of 1996 to the middle of 2001.
(e) The range of C will be all numbers y such that (t, y) appears on the graph.
Examining the graph gives an approximate range of 60 y 140. ■
THE VERTICAL LINE TEST
The following fact distinguishes graphs of functions from other graphs.
To see why this is true, consider Figure 3–27, in which the graph intersects the
vertical line at two points. If this were the graph of a function f, then we would
have f (3) 2 [because (3, 2) is on the graph] and f (3) 1 [because (3, 1) is
on the graph]. This means that the input 3 produces two different outputs, which
is impossible for a function. Therefore, Figure 3–27 is not the graph of a function.
A similar argument works in the general case.
Care must be used when applying the Vertical Line test to a calculator graph.
For example, if we graph g(x) 4 x
10
2 in the standard viewing window, it
looks like it fails the vertical line test near x 1, among other places (Figure
3–28). But if we use the window with 1 x 1.25, 5 y 5 we see that g(x)
does pass the vertical line test at x 1 (Figure 3–29).
SECTION 3.3 Graphs of Functions 169
Vertical
Line Test
The graph of a function y f (x) has this property:
No vertical line intersects the graph more than once.
Conversely, any graph with this property is the graph of a function.
3
(3, 2)
(3, −1)
x
y
Figure 3–27
5
1.25
1
5
Figure 3–29
10
10
10
10
Figure 3–28
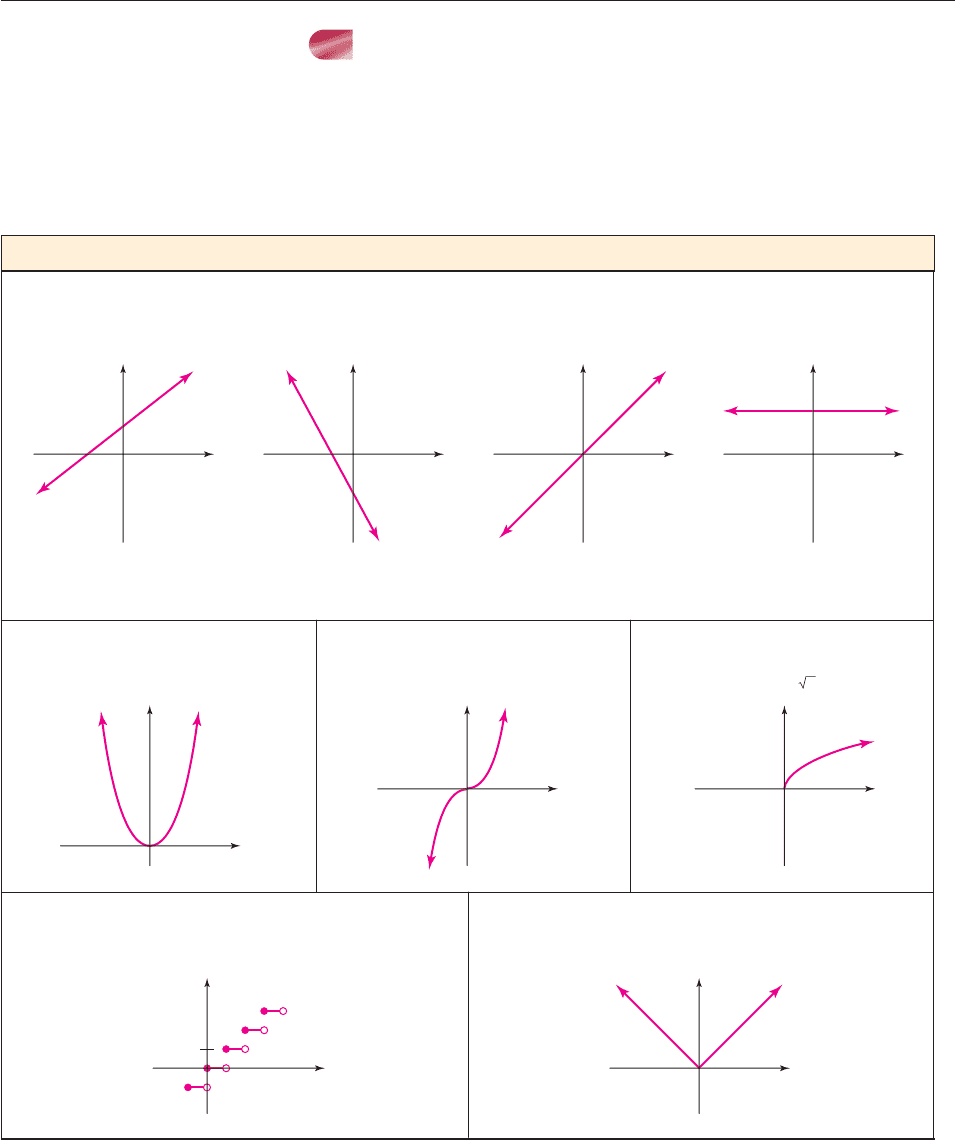
CATALOG OF BASIC FUNCTIONS
As was noted at the beginning of this section, there are a number of functions
whose graphs you should know by heart. The ones in this section are listed below;
others will be added as we go along. The entire catalog appears on the inside front
cover of this book.
170 CHAPTER 3 Functions and Graphs
Positive Slope
(m > 0)
f(x) = mx + b
x
y
Negative Slope
(m < 0)
Linear Functions
Square Root Function
f(x) = mx + b
x
y
Identity Function
(m = 1)
f(x) = x
x
y
x
y
Cube Function
Greatest Integer Function Absolute Value Function
f(x) = x
3
x
y
Square Function
f(x) = x
2
x
y
Constant Function
(m = 0)
f(x) = b
x
y
b
f(x) = x
f(x) = ⏐x⏐
x
y
f(x) = x
x
y
1
1
CATALOG OF BASIC FUNCTIONS—PART 1

SECTION 3.3 Graphs of Functions 171
EXERCISES 3.3
In Exercises 1–4, state whether or not the graph is the graph of
a function. If it is, find f (3).
1.
2.
3.
4.
In Exercises 5–11, sketch the graph of the function, being sure
to indicate which endpoints are included and which ones are
excluded.
5. f (x) 2 x 6. f (x) x
7. g(x) x [This is not the same function as in Exercise 6.]
x
2
if x 1
8. f (x)
2x 3ifx 1
2
0
2
x
y
2
0
2
x
y
2−2
−2
0
1
x
y
231−1−2−3
0
2
−2
x
y
2u 2ifu 3
9. k(u)
u u if 3 u 1
2u
2
if u 1
10. As of this writing, U.S. postage rates for large envelopes are
80 cents for the first ounce (or fraction thereof) plus 17 cents
for each additional ounce or fraction thereof (see Example 5).
Assume that each large envelope carries one 80 cent stamp
and as many 17 cent stamps as necessary. Then the number of
stamps required for a large envelope is a function of the
weight of the envelope in ounces. Call this function the
postage stamp function.
(a) Describe the rule of the postage stamp function alge-
braically.
(b) Sketch the graph of the postage stamp function.
11. A common mistake is to graph the function f in Exam-
ple 6 by graphing both y x
2
and y x 2 on the same
screen (with no restrictions on x). Explain why this graph
could not possibly be the graph of a function.
Exercises 12–21 deal with the graph of g shown in the figure.
12. Is g a function? Why or why not?
13. What is the domain of g?
14. What is the range of g?
15. Find the approximate intervals where g is increasing.
16. Find the approximate intervals where g is decreasing.
17. If t 2, then g(t 1.5) ?
18. If t 2, then g(t) g(1.5) ?
19. If t 2, then g(t) 1.5 ?
20. For what values of x is g(x) 0?
21. For what values of a is g(a) 1?
In Exercises 22–24, (a) Use the fact that the absolute value func-
tion is piecewise-defined (see Example 7) to write the rule of the
given function as a piecewise-defined function whose rule does
not include any absolute value bars. (b) Graph the function.
22. g(x) x 4 23. h(x) x/2 2
24. g(x) x 3
25. Show that the function f (x) x x 2 is constant on
the interval [0, 2]. [Hint: Use the definition of absolute
value (see Example 7) to compute f (x) when 0 x 2.]
1
−1
−2
−2
2
3
3421
−1−3
5

In Exercises 26–31, find the approximate location of all local
maxima and minima of the function.
26. f (x) x
3
x 27. g(t) 16 t
2
28. h(x)
x
2
x
1
29. k(x) x
3
3x 1
30. l(x)
1
1
x
2
31. m(x) x
3
In Exercises 32–35, find the approximate intervals on which
the function is increasing, those on which it is decreasing, and
those on which it is constant.
32. f(x) x 1 x 1
33. f(x) x
3
8x
2
8x 5
34. f(x)
x
35. f(x)
1
x
36. Let F(x) the U.S. federal debt in year x, and let p(x) the
federal debt as a percent of the gross domestic product in
year x. The graphs of these functions appear below.* Explain
why the graph of F is increasing from 1996–2001, while the
graph of p is decreasing during that period.
Gross Federal Debt
(billions of dollars)
F(x)
9000
8000
6000
7000
4000
5000
3000
2000
1000
0
Federal Debt as a Percent of Gross Domestic Product
1990 1992 1994 1996
p(x)
1998 2000
80
70
50
60
40
30
20
10
1990 1992 1994 1996 1998 2000
2002
2002
2004
2004
Percent
172 CHAPTER 3 Functions and Graphs
37. Find the dimensions of the rectangle with perimeter
100 inches and largest possible area, as follows.
(a) Use the figure to write an equation in x and z that ex-
presses the fact that the perimeter of the rectangle is
100.
(b) The area A of the rectangle is given by A xz (why?).
Write an equation that expresses A as a function of x.
[Hint: Solve the equation in part (a) for z, and substitute
the result in the area equation.]
(c) Graph the function in part (b), and find the value of x
that produces the largest possible value of A. What is z
in this case?
38. Find the dimensions of the rectangle with area 240 square
inches and smallest possible perimeter, as follows.
(a) Using the figure for Exercise 37, write an equation for
the perimeter P of the rectangle in terms of x and z.
(b) Write an equation in x and z that expresses the fact that
the area of the rectangle is 240.
(c) Write an equation that expresses P as a function of x.
[Hint: Solve the equation in part (b) for z, and substitute
the result in the equation of part (a).]
(d) Graph the function in part (c), and find the value of x
that produces the smallest possible value of P. What is z
in this case?
39. Find the dimensions of a box with a square base that has a
volume of 867 cubic inches and the smallest possible sur-
face area, as follows.
(a) Write an equation for the surface area S of the box in
terms of x and h. [Be sure to include all four sides, the
top, and the bottom of the box.]
(b) Write an equation in x and h that expresses the fact that
the volume of the box is 867.
(c) Write an equation that expresses S as a function of x.
[Hint: Solve the equation in part (b) for h, and substi-
tute the result in the equation of part (a).]
(d) Graph the function in part (c), and find the value of x
that produces the smallest possible value of S. What is h
in this case?
40. Find the radius r and height h of a cylindrical can with a sur-
face area of 60 square inches and the largest possible vol-
ume, as follows.
x
x
h
x
z
*Graphs prepared by U.S. Census Bureau, based on data from the U.S.
Office of Management and Budget.

(a) Write an equation for the volume V of the can in terms
of r and h.
(b) Write an equation in r and h that expresses the fact that
the surface area of the can is 60. [Hint: Think of cutting
the top and bottom off the can; then cut the side of the
can lengthwise and roll it out flat; it’s now a rectangle.
The surface area is the area of the top and bottom plus
the area of this rectangle. The length of the rectangle is
the same as the circumference of the original can
(why?).]
(c) Write an equation that expresses V as a function of r.
[Hint: Solve the equation in part (b) for h, and substi-
tute the result in the equation of part (a).]
(d) Graph the function in part (c), and find the value of r
that produces the largest possible value of V. What is h
in this case?
41. Match each of the functions (a)–(e) with the graph that best
fits the situation.
x
(i)
y
(ii)
x
y
(v)
x
y
(iii)
x
y
(iv)
x
y
r
h
SECTION 3.3 Graphs of Functions 173
(a) The phases of the moon as a function of time;
(b) The demand for a product as a function of its price;
(c) The height of a ball thrown from the top of a building as
a function of time;
(d) The distance a woman runs at constant speed as a func-
tion of time;
(e) The temperature of an oven turned on and set to 350° as
a function of time.
In Exercises 42 and 43, sketch a plausible graph of the given
function. Label the axes and specify a reasonable domain and
range.
42. The distance from the top of your head to the ground as you
jump on a trampoline as a function of time.
43. The temperature of an oven that is turned on, set to
350°, and 45 minutes later turned off as a function of
time.
44. A plane flies from Austin, Texas, to Cleveland, Ohio, a
distance of 1200 miles. Let f be the function whose rule is
f (t) distance (in miles) from Austin at time t hours.
Draw a plausible graph of f under the given circum-
stances. [There are many possible correct answers for
each part.]
(a) The flight is nonstop and takes less than 4 hours.
(b) Bad weather forces the plane to land in Dallas (about
200 miles from Austin), remain overnight (for 8 hours),
and continue the next day.
(c) The flight is nonstop, but owing to heavy traffic, the
plane must fly in a holding pattern over Cincinnati
(about 200 miles from Cleveland) for an hour before
going on to Cleveland.
In Exercises 45–46, the graph of a function f is shown. Find
and label the given points on the graph.
45. (a) (k, f (k))
(b) (k, f (k))
(c) (k, f (k))
46. (a) (k, f (k))
(b) (k, .5f (k))
(c) (.5k, f (.5k))
(d) (2k, f (2k))
k
k

47. The graph of the function f, whose rule is f(x) average
interest rate on a 30-year fixed-rate mortgage in year x, is
shown in the figure.* Use it to answer these questions (rea-
sonable approximations are OK).
(a) Compute f (1977), f (1982) and f (2000)
(b) In what year between 1990 and 2006 were rates the
lowest? The highest?
(c) During what three-year period were rates changing
the fastest? How do you determine this from the
graph?
48. The annual percentage changes in various consumer price
indexes (CPIs) are shown in the figure.
†
Use it to answer the
following questions. In each case, explain how you got your
answer from the graph.
(a) Did the CPI for medical care increase or decrease from
1990 to 1996?
(b) During what time intervals was the CPI for fuel oil
increasing?
(c) If the CPI for fuel oil stood at 91 at the beginning of
1999, approximately what was it at the beginning of
2000?
50
40
60
20
10
30
1990
Percent
1992 1994 1996
Fuel oil
All items
Medical care
1998 2000
−10
−20
0
1976 1980 1984 1988 1992 1996
15
18%
12
9
6
2000 2004
174 CHAPTER 3 Functions and Graphs
49. The Cleveland temperature graph from Example 2 of
Section 3.1, is reproduced below. Let T(x) denote the
temperature at time x hours after midnight.
Determine whether the following statements are true or
false.
(a) T(4
3) T(4)
T(3)
(b) T(4
3) 4
T(3)
(c) T(4 14) T(4) T(14)
50. Draw the graph of a function f that satisfies the following
four conditions:
(i) domain f [2, 4]
(ii) range f [5, 6]
(iii) f(1) f(3)
(iv) f
1
2
0
51. Sketch the graph of a function f that satisfies these five con-
ditions:
(i) f (1) 2
(ii) f (x) 2 when x is in the interval 1,
1
2
(iii) f (x) starts decreasing when x 1
(iv) f (3) 3 f (0)
(v) f (x) starts increasing when x 5
[Note: The function whose graph you sketch need not be
given by an algebraic formula.]
52. Wireless telephone services are growing rapidly. The table
shows the industry’s revenue (in billions of dollars) over a
five-year period.*
4812
A.M. P.M.
Noon
Time of Day
Temperature (degrees Fahrenheit)
16 20 24
x
y
40°
50°
60°
70°
*Federal Home Mortgage Corporation.
†
Graph prepared by U.S. Census Bureau, based on data from the Bureau
of Labor Statistics.
Year Revenue
1999 40.018
2000 52.966
2002 76.508
2003 87.624
2004 100.600
*New York Times 2006 Almanac.

(a) Make a scatter plot of the data, with x 0 correspon-
ding to 1999.
(b) Use linear regression to find a function that models this
data. Assume that the model remains accurate.
(c) Use the model to estimate the revenue in 2001.
(d) When will revenue reach $170 billion?
53. The percentage of adults in the United States who smoke
has been decreasing, as shown in the table.*
(a) Make a scatter plot of the data, with x 0 correspon-
ding to 1965.
(b) Use linear regression to find a function that models this
data.
(c) Use the model to estimate the percentage of smokers in
1991 and 2013. [For comparison purposes, the actual
figure for 1991 is 25.8%.]
(d) If this model remains accurate, when will less than 15%
of adults smoke?
(e) According to this model, will smoking even disappear
entirely? If so, when?
In Exercises 54 and 55, sketch the graph of the equation.
54. x y 1 55. y x
2
THINKERS
56. Assume that on Sunday you read a long book containing a
lot of factual material. Assume that by Monday you only
remember 2/3 of the material. On Tuesday you remember
2/3 of what you remembered on Monday. On Wednesday
SPECIAL TOPICS 3.3.A Parametric Graphing 175
Year Percent Who Smoke
1965 42.5
1974 37.0
1980 33.3
1987 29.2
1994 25.4
2000 22.9
2005 20.9
*
Centers for Disease Control and Prevention.
you remember 2/3 of what you remembered on Tuesday, and
so on. Let f(t) be the percent of the material you remember t
days after Sunday. (So f(0) 100, and f(1) 66
2
3
). Sketch
f(t) from t 0 to t 12.
57. For each m, let f(m) be the largest real solution to this equation:
x
2
4x m 0.
(a) Find the domain of f
(b) Find the range of f
(c) Sketch a graph of f
x
2
if x is an integer
58. Let f(x)
x if x is not an integer
Sketch f.
59. A jogger begins her daily run from her home. The graph
shows her distance from home at time t minutes. The graph
shows, for example, that she ran at a slow but steady pace
for 10 minutes, then increased her pace for 5 minutes, all
the time moving farther from home. Describe the rest of
her run.
60. The graph shows the speed (in mph) at which a driver is
going at time t minutes. Describe his journey.
Speed
Time
1791115
10
20
30
40
3020
Distance
Time
10
605040
■ Obtain graphs of parametric equations.
■ Graph equations that define x as a function of y.
As we have seen, functional notation is an excellent way to describe certain kinds
of relationships and curves. It is less helpful, however, when describing curves
3.3.A SPECIAL TOPICS Parametric Graphing
Section Objectives
