Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.


The product and quotient of functions f and g are the functions defined by
the rules
( fg)(x) f (x)g(x) and
g
f
(x)
g
f(
(
x
x
)
)
.
The domain of fg consists of all real numbers in both the domain of f and the do-
main of g. The domain of f/g consists of all real numbers x in both the domain of
f and the domain of g such that g(x) 0.
EXAMPLE 2
If f (x) 3x
and g(x) x
2
1, find the rules of the functions fg and f/g and
their domains.
SOLUTION The rules are
( fg)(x) f (x)g(x)
g
f
(x)
g
f (
(
x
x
)
)
3x
(x
2
1)
(3x
) x
2
3x
x
2
3x
1
The domain of fg consists of all numbers x in both the domain of f (all nonnega-
tive real numbers) and the domain of g (all real numbers), that is, all x 0. The
domain of f/g consists of all these x for which g (x) 0, that is, all nonnegative
real numbers except x 1. ■
If c is a real number and f is a function, then the product of f and the constant
function g(x) c is usually denoted cf. For example, if the function
f (x) x
3
x 2,
and c 5, then 5f is the function given by
(5f )(x) 5
f (x)
5(x
3
x 2)
5x
3
5x 10
COMPOSITION OF FUNCTIONS
Another way of combining functions is illustrated by the function h(x)
x
3
.
To compute h(4), for example, you first find 4
3
64 and then take the square
root 64 8. So the rule of h may be rephrased as follows:
First apply the function f (x) x
3
,
Then apply the function g(t) t
to the result.
The same idea can be expressed in functional notation like this:
first apply f then apply g to the result
x ———— f (x) ————————— g( f (x)).
xx
3
x
3
apply h
196 CHAPTER 3 Functions and Graphs

So the rule of h may be written as h(x) g( f(x)), where f (x) x
3
and g(t) t
.
We can think of h as being made up of two simpler functions f and g, or we can think
of f and g being “composed” to create the function h. Both viewpoints are useful.
EXAMPLE 3
Suppose f (x) 4x
2
1 and g(t)
t
1
2
. Define a new function h whose rule is
“first apply f; then apply g to the result.” In functional notation,
first apply f then apply g to the result
x ———— f (x) ————————— g( f (x)).
So the rule of the function h is h(x) g( f (x)). Evaluating g( f (x)) means that
whenever t appears in the formula for g(t), we must replace it by f (x) 4x
2
1:
h(x) g( f (x))
f (x)
1
2
(4x
2
1
1) 2
4x
2
1
3
■
The function h in Example 3 is an illustration of the following definition.
The symbol “g f ” is read “g circle f ” or “f followed by g.” (Note the order
carefully; the functions are applied right to left.) So the rule of the composite
function is
(g f )(x) g( f (x)).
EXAMPLE 4
If f (x) 2x 5 and g(t) 3t
2
2t 4, then find
( f
g)(2), (g
f )(1), (g
f )(5), (g
f )(x).
SOLUTION
( f g)(2) f (g(2))
f (3
2
2
2
2 4)
f (20)
2
20 5
45.
SECTION 3.5 Operations on Functions 197
Composite
Functions
Let f and g be functions. The composite function of f and g defined as
follows.
For input x, the output is g( f (x)).
This composite function is denoted g f.
Similarly, (g f )(1) g( f (1))
g(2(1) 5)
g(3)
3
3
2
2
3 4
37.

The value of a composite function can also be computed like this:
(g f )(5) g( f (5)) 3( f (5)
2
) 2( f (5)) 4 3(15
2
) 2(15) 4 709.
and
(g f )(x) g( f (x)) 3(2x 5)
2
2(2x 5) 4 12x
2
64x 89. ■
The domain of g f is determined by this convention.
EXAMPLE 5
Find the rule and domain of g f, when f (x) x
and g(t) t
2
5.
SOLUTION
(g f )(x) g( f (x)) ( f (x))
2
5 (x
)
2
5 x 5.
Although x 5 is defined for every real number x, the domain of g f is not the
set of all real numbers. The domain of g is the set of all real numbers, but the func-
tion f (x) x
is defined only when x 0. So the domain of g f is the set of non-
negative real numbers, that is, the interval [0, ). ■
EXAMPLE 6
Write the function h(x)
3x
2
1
in two different ways as the composite of
two functions.
SOLUTION Let f (x) 3x
2
1 and g(x) x
.* Then
(g f )(x) g( f (x)) g(3x
2
1)
3x
2
1
h(x).
Similarly, h is also the composite j k, where j(x) x 1
and k(x) 3x
2
:
( j k)(x) j(k(x)) j(3x
2
)
3x
2
1
h(x). ■
EXAMPLE 7
If k(x) (x
2
2x x
)
3
, then k is g f, where f (x) x
2
2x x
and
g(x) x
3
because
(g f )(x) g( f (x)) g(x
2
2x x
) (x
2
2x x
)
3
k(x). ■
198 CHAPTER 3 Functions and Graphs
Domain of
g f
The domain of the composite function g f is the set of all real numbers x
such that x is in the domain of f and f (x) is in the domain of g.
*Now that you have the idea of composite functions, we’ll use the same letter for the variable in both
functions.
TECHNOLOGY TIP
Evaluating composite functions is easy
on calculators other than TI-86 and
most Casio calculators. If the func-
tions are entered in the equation mem-
ory as y
1
g(x ) and y
2
h(x)
(with f in place of y on HP-39gs), then
keying in y
2
(y
1
(5)) ENTER produces the
number h(g(5)).
On TI-86 and most Casio calcu-
lators, this syntax does not produce
h(g(5)); it produces
h(x )
g(x )
5
for whatever number is stored in the
x-memory.

By using the function operations above, a complicated function may be con-
sidered as being built up from simple parts.
EXAMPLE 8
The function
f (x)
3x
2
x
3
4x
1
5
may be considered as the composite f g h, where
h(x)
3x
2
x
3
4x
1
5
and g(x) x
,
since
(g h)(x) g(h(x)) g
3x
2
x
3
4x
1
5
3x
2
x
3
4x
1
5
f (x).
The function
h(x)
3x
2
x
3
4x
1
5
is the quotient , where
p(x) 3x
2
4x 5 and q(x) x
3
1.
The function p(x) 3x
2
4x 5 may be written p k s r, where
k(x) 3x
2
, s(x) 4x, r(x) 5.
The function k, in turn, can be considered as the product 3I
2
, where I is the iden-
tity function [whose rule is I(x) x]:
(3I
2
)(x) 3(I
2
(x)) 3(I(x)I(x)) 3
x
x 3x
2
k(x).
Similarly, s(x) (4I)(x) 4I (x) 4x. The function q(x) x
3
1 may be
“decomposed” in the same way.
Thus, the complicated function f is just the result of performing suitable
operations on the identity function I and various constant functions. ■
As you may have noticed, there are two possible ways to form a compos-
ite function from two given functions. If f and g are functions, we can consider
either
(g f )(x) g( f (x)), [the composite of f and g]
( f g)(x) f (g(x)). [the composite of g and f]
The order is important, as we shall now see:
g f and f g usually are not the same function.
p
q
SECTION 3.5 Operations on Functions 199

EXAMPLE 9
If f (x) x
2
and g(x) x 3, then
( f g)(x) f (g(x)) (g f )(x) g( f (x))
f (x 3) g(x
2
)
(x 3)
2
x
2
3,
x
2
6x 9.
Obviously, g f f g, since, for example, they have different values at x 0.
■
200 CHAPTER 3 Functions and Graphs
APPLICATIONS
Compositions of functions arise in applications involving several functional rela-
tionships simultaneously. In such cases, one quantity may have to be expressed as
a function of another.
EXAMPLE 10
A circular puddle of liquid is evaporating and slowly shrinking in size. After t
minutes, the radius r of the puddle measures
2t
1
8
3
inches; in other words, the
radius is a function of time. The area A of the puddle is given by A pr
2
, that is,
area is a function of the radius r. We can express the area as a function of time
by substituting r
2t
1
8
3
in the area equation:
A pr
2
p
2t
1
8
3
2
.
This amounts to forming the composite function f g, where f (r) pr
2
and
g(t)
2t
1
8
3
:
( f g)(t) f (g(t)) f
2t
1
8
3
p
2t
1
8
3
2
.
When area is expressed as a function of time, it is easy to compute the area of the
puddle at any time. For instance, after 12 minutes, the area of the puddle is
A p
2t
1
8
3
2
p
2
4
9
p
1.396 square inches. ■
18
2
12 3
CAUTION
Don’t confuse the product function fg with the composite function f g (g followed by f ). For
instance, if f (x) 2x
2
and g(x) x 3, then the product fg is given by
(fg)(x) f (x)g(x) 2x
2
(x 3) 2x
3
6x
2
.
It is not the same as the composite f g because
(f g)(x) f(g(x )) f (x 3) 2(x 3)
2
2x
2
12x 18.

EXAMPLE 11
At noon, a car leaves Podunk on a straight road, heading south at 45 mph, and a
plane 3 miles above the ground passes over Podunk heading east at 350 mph.
(a) Express the distance r traveled by the car and the distance s traveled by the
plane as functions of time.
(b) Express the distance d between the plane and the car in terms of r and s.
(c) Express d as a function of time.
(d) How far apart were the plane and the car at 1:30 P.M.?
SOLUTION
(a) Traveling at 45 mph for t hours, the car will go a distance of 45t miles. Hence,
the equation r 45t expresses the distance r as a function of the time t. Sim-
ilarly, the equation s 350t expresses the distance s as a function of the time t.
(b) To express the distance d as a function of r and s, consider Figure 3–50.
Figure 3–50
Right triangle PQD and the Pythagorean Theorem show that (PD)
2
r
2
s
2
;
hence, PD
r
2
s
2
. Applying the Pythagorean Theorem to right triangle
PDC, we have
d
2
3
2
(PD)
2
d
2
3
2
(r
2
s
2
)
2
d
2
9 r
2
s
2
d
9 r
2
s
2
.
(c) The preceding equation expresses d in terms of r and s. By substituting r 45t
and s 350t in this equation, we can express d as a function of the time t:
d
9 r
2
s
2
d 9 (4
5t)
2
(350t)
2
d 9 20
25t
2
122,50
0t
2
9 12
4,525t
2
.
(d) At 1:30 P.M., we have t 1.5 (since noon is t 0). At this time,
d
9 12
4,525t
2
9 12
4,525(
1.5)
2
280,19
0.25
529.33 miles. ■
QP
P
ss
r
r
d
DD
C
C
South
East
Podunk
33
SECTION 3.5 Operations on Functions 201

202 CHAPTER 3 Functions and Graphs
EXERCISES 3.5
In Exercises 1–4, find ( f g)(x), ( f g)(x), and (g f )(x).
1. f(x) 3x 2, g(x) x
3
2. f(x) x
2
2, g(x) x
2
4x 2
3. f(x) 1/x, g(x) x
2
2x 5
4. f(x) x
, g(x) x
2
1 x
In Exercises 5–8, find ( fg)(x), ( f/g)(x), and (g/f )(x).
5. f(x) 3x 2, g(x) x
3
6. f(x) 4x
2
x
4
, g(x)
x
2
4
7. f(x) x 5, g(x) x 5
8. f(x)
x
2
1
, g(x) x 1
In Exercises 9–12, find the domains of fg and f/g.
9. f(x) x
2
1, g(x) 1/x
10. f(x) x
2
2, g(x)
x
2
1
2
11. f(x) 4 x
2
, g(x) 3x 4
12. f(x) 3x
2
x
4
2, g(x) 4x 3
In Exercises 13–16, find the indicated values, where
g(t) t
2
t and f(x) 1 x.
13. g( f(0))
14. ( f g)(3)
15. g( f(2) 3)
16. f(2g(1))
In Exercises 17–20, find (g f )(3), ( f g)(1), and ( f f )(0).
17. f(x) 3x 2, g(x) x
2
18. f(x) x 2, g(x) x
2
19. f(x) x, g(x) 3
20. f(x) x
2
1, g(x) x
In Exercises 21–24, find the rule of the function f g, the
domain of f g, the rule of g f, and the domain of g f.
21. f(x) 3x 2, g(x) x
3
22. f(x) 1/x, g(x) x
23. f(x)
2x
1
1
, g(x) x
2
1
24. f(x) (x 3)
2
, g(x) x
3
In Exercises 25–28, find the rules of the functions ff and f f.
25. f(x) x
3
26. f(x) (x 1)
2
27. f(x) 1/x 28. f (x)
x
1
1
In Exercises 29–32, verify that ( f g)(x) x and (g f )(x) x
for every x.
29. f(x) 9x 8, g(x)
x
9
8
30. f(x)
3
x 1
, g(x) x
3
1
31. f(x)
3
x
2, g(x) (x 2)
3
32. f(x) 2x
3
5, g(x)
3
x
2
5
Exercises 33 and 34 refer to the function f whose graph is
shown in the figure.
33. Let g be the composite function f f.
Use the graph of f to fill in the following table (approximate
where necessary).
34. Use the information obtained in Exercise 33 to sketch the
graph of the function g.
In Exercises 35–38, fill the blanks in the given table. In each
case the values of the functions f and g are given by these tables:
−2 −1
−1
−2
1
2
−3
123−3
xf(x) g(x) f( f(x))
4
3
20 1
1
0
1
2
3
4
xf(x)
13
25
31
42
53
tg(t)
15
24
34
43
52
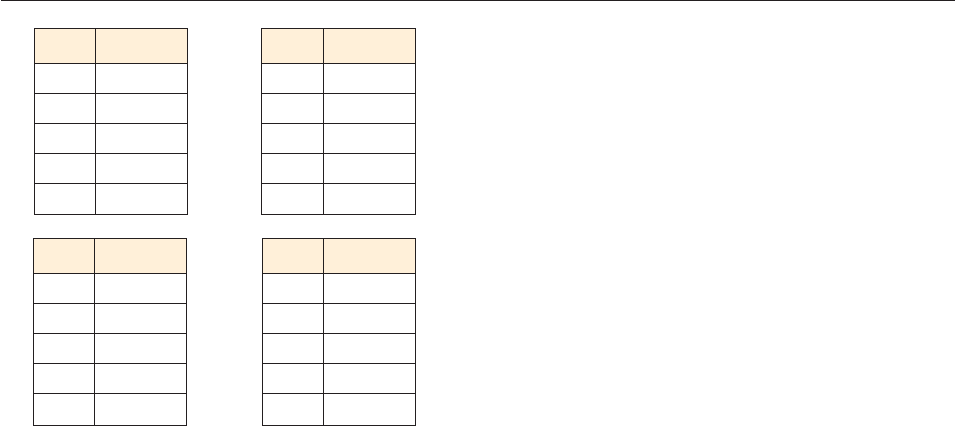
x ( f f )(x)
1
2
33
4
5
t (g g)(t)
1
2
3
44
5
x (g f )(x)
14
2
35
4
5
t ( f g)(t)
1
22
3
4
5
35. 36.
37. 38.
In Exercises 39–42, write the given function as the composite
of two functions, neither of which is the identity function, as in
Examples 6 and 7. (There may be more than one way to do
this.)
39. f(x)
3
x
2
2
40. g(x) x 3
3
x 3
41. h(x) (7x
3
10x 17)
7
42. f(x)
3x
2
1
5x 7
43. If f(x) x 1 and g(t) t
2
, then
(g f )(x) g( f(x)) g(x 1) (x 1)
2
x
2
2x 1
Find two other functions h(x) and k(t) such that
(k h)(x) x
2
2x 1.
44. If f is any function and I is the identity function, what are
f I and I f ?
In Exercises 45–48, determine whether the functions f g and
g f are defined. If a composite is defined, find its domain.
45. f(x) x
3
, g(x) x
46. f(x) x
2
1, g(x) x
47. f(x) x 10
, g(x) 5x
48. f(x) x
2
, g(x) x
49. (a) If f(x) 2x
3
5x 1, find f(x
2
).
(b) If f (x) 2x
3
5x 1, find ( f (x))
2
.
(c) Are the answers in parts (a) and (b) the same? What can
you conclude about f(x
2
) and ( f (x))
2
?
50. Give two examples of functions f such that
f
1
x
f(
1
x)
.
SECTION 3.5 Operations on Functions 203
In Exercises 51 and 52, graph both f g and g f on the same
screen. Use the graphs to determine whether f g is the same
function as g f.
51. f(x) x
5
x
3
x; g(x) x 2
52. f(x) x
3
x; g(x)
3
x 1
In Exercises 53–56, find g f, and find the difference quotient
of the function g f.
53. f(x) x 3; g(x) x
2
1
54. f(x) 2x; g(x) 8x
55. f(x) x 1; g(x)
x
2
1
56. f(x) x
3
; g(x) x 2
57. (a) What is the area of the puddle in Example 10 after one
day? After a week? After a month?
(b) Does the puddle ever totally evaporate? Is this realistic?
Under what circumstances might this area function be
an accurate model of reality?
58. In a laboratory culture, the number N(d ) of bacteria (in
thousands) at temperature d degrees Celsius is given by the
function
N(d)
d
90
1
20 (4 d 32).
The temperature D(t) at time t hours is given by the function
D(t) 2t 4(0 t 14).
(a) What does the composite function N D represent?
(b) How many bacteria are in the culture after 4 hours?
After 10 hours?
59. A certain fungus grows in a circular shape. Its diameter
after t weeks is 6
t
2
50
10
inches.
(a) Express the area covered by the fungus as a function of
time.
(b) What is the area covered by the fungus when t 0?
What area does it cover at the end of 8 weeks?
(c) When is its area 25 square inches?
60. Tom left point P at 6 A.M. walking south at 4 mph. Anne left
point P at 8
A.M. walking west at 3.2 mph.
(a) Express the distance between Tom and Anne as a func-
tion of the time t elapsed since 6
A.M.
(b) How far apart are Tom and Anne at noon?
(c) At what time are they 35 miles apart?
61. As a weather balloon is inflated, its radius increases at the
rate of 4 centimeters per second. Express the volume of the
balloon as a function of time and determine the volume of
the balloon after 4 seconds. [Hint: The volume of a sphere
of radius r is 4pr
3
/3.]
62. Express the surface area of the weather balloon in Exercise
61 as a function of time. [Hint: The surface area of a sphere
of radius r is 4pr
2
.]
63. Charlie, who is 6 feet tall, walks away from a streetlight that
is 15 feet high at a rate of 5 feet per second, as shown in the
figure on the next page. Express the length s of Charlie’s

shadow as a function of time. [Hint: First use similar trian-
gles to express s as a function of the distance d from the
streetlight to Charlie.]
64. A water-filled balloon is dropped from a window 120 feet
above the ground. Its height above the ground after t sec-
onds is 120 16t
2
feet. Laura is standing on the ground
40 feet from the point where the balloon will hit the ground,
as shown in the figure.
d
40 feet
6 feet
ds
15 feet
204 CHAPTER 3 Functions and Graphs
(a) Express the distance d between Laura and the balloon
as a function of time.
(b) When is the balloon exactly 90 feet from Laura?
THINKER
65. Find a function f (other than the identity function) such that
( f f f )(x) x for every x in the domain of f. [Several cor-
rect answers are possible.]
66. If f is an increasing function, does f f have to be increasing?
Why or why not?
67. Let f(x) x
2
.2
(a) Using a calculator, compute f(0), ( f f )(0),
( f f f )(0),... etc. What happens as you keep going?
(b) Does the same thing happen if you look at f(1), (f f ) (1),
( f f f )(1),...?
(c) Repeat parts (a) and (b) using f(x) x
2
.9.
(d) Repeat parts (a) and (b) using f(x) x
2
1.3.
[Hint: You may be able to save yourself some keystrokes
using the ANS and ENTRY keys on your calculator.]
3.6 Rates of Change
■ Determine the average rate of change of a function on an
interval.
■ Understand average rate of change as applied to real-life
situations.
■ Interpret average rate of change graphically.
■ Use the difference quotient to find the average rate of change
over very small intervals.
■ Approximate the instantaneous rate of change of a function at a
point.
Section Objectives

Rates of change play a central role in the analysis of many real-world situations.
To understand the basic ideas involved in rates of change, we take another look at
the falling rock from Sections 3.1 and 3.2. We saw that when the rock is dropped
from a high place, then the distance it travels (ignoring wind resistance) is given
by the function
d(t) 16t
2
with distance d(t) measured in feet and time t in seconds. The following table
shows the distance the rock has fallen at various times:
To find the distance the rock falls from time t 1 to t 3, we note that at the
end of three seconds, the rock has fallen d(3) 144 feet, whereas it had fallen
only d(1) 16 feet at the end of one second. So during this time interval, the rock
traveled
d(3) d(1) 144 16 128 feet.
The distance traveled by the rock during other time intervals can be found
similarly:
The same procedure works in general:
The distance traveled from time t a to time t b is d(b) d(a) feet.
In the preceding chart, the length of each time interval can be computed by
taking the difference between the two times. For example, from t 1 to t 4 is
a time interval of length 4 1 3 seconds. Similarly, the interval from t 2 to
t 3.5 is of length 3.5 2 1.5 seconds, and in general,
The time interval from t a to t b is an interval of b a seconds.
Since Distance Average speed Time,
Average speed
Di
T
s
i
t
m
an
e
ce
in
t
t
r
e
a
r
v
v
e
a
l
l
ed
.
Hence, the average speed over the time interval from t a to t b is
Average speed
Di
T
s
i
t
m
an
e
ce
in
t
t
r
e
a
r
v
v
e
a
l
l
ed
d(b
b
)
d
a
(a)
.
For example, to find the average speed from t 1 to t 4, apply the preceding
formula with a 1 and b 4:
Average speed
d(4
4
)
d
1
(1)
25
4
6
1
16
24
3
0
80 ft per second.
SECTION 3.6 Rates of Change 205
Time t 0 1 2 3 3.5 4 4.5 5
Distance d(t) 0 16 64 144 196 256 324 400
Time Interval Distance Traveled
t 1 to t 4 d(4) d(1) 256 16 240
t 2 to t 3.5 d(3.5) d(2) 196 64 132
t 2 to t 4.5 d(4.5) d(2) 324 64 260
