Hungerford T.W., Shaw D.J. Contemporary Precalculus: A Graphing Approach
Подождите немного. Документ загружается.

Similarly, the average speed from t 2 to t 4.5 is
d(4
4
.5
.5
)
d
2
(2)
3
4
2
.
4
5
6
2
4
2
2
6
.5
0
104 ft per second.
The units in which average speed is measured here (feet per second) indi-
cate the number of units of distance traveled during each unit of time, that is,
the rate of change of distance (feet) with respect to time (seconds). The
preceding discussion can be summarized by saying that the average speed (rate
of change of distance with respect to time) as time changes from t a to t b
is given by
Average speed Average rate of change
Ch
C
a
h
n
a
g
n
e
g
i
e
n
in
di
t
s
i
t
m
an
e
ce
d(b
b
)
d
a
(a)
.
Although speed is the most familiar example, rates of change play a role in many
other situations as well, as illustrated in Examples 1–3 below. Consequently, we
define the average rate of change of any function as follows.
EXAMPLE 1
Heidi started a big driving trip at 3 P.M. The odometer reading on her car said
103,846. She finished her trip at 9 P.M., and now the odometer read 104,176. What
was her average speed during the trip?
SOLUTION
Her average speed was
Di
T
s
i
t
m
an
e
ce
in
t
t
r
e
a
r
v
v
e
a
l
l
ed
. Her distance traveled was 104,176
103,846 miles. Her time interval was 9 3 hours. So her average speed was
104,176
9
1
3
03,846
3
6
30
ho
m
u
i
r
l
s
es
55 miles per hour. ■
EXAMPLE 2
A large heavy-duty balloon is being filled with water. Its approximate volume (in
gallons) is given by
V(x)
5
x
5
3
,
206 CHAPTER 3 Functions and Graphs
Average Rate
of Change
Let f be a function. The average rate of change of f (x) with respect to x as
x changes from a to b is the number
C
C
ha
h
n
a
g
n
e
ge
in
in
f (
x
x)
f (b
b
)
f
a
(a)
.
where x is the radius of the balloon (in inches). Find the average rate of change of
the volume of the balloon as the radius increases from 5 to 10 inches.
SOLUTION
C
C
h
h
a
a
n
n
g
g
e
e
in
in
v
r
o
a
l
d
u
i
m
us
e
V(1
1
0
0
)
V
5
(5)
18.1
1
8
0
2
5
.27
15
5
.91
3.182 gallons per inch. ■
EXAMPLE 3
According to the Encyclopedia Britannica almanac, these are the estimated num-
ber of cell phone users in the United States, from 1993 to 2004.
Let f (t) be the number of cell phone users in year t. Find the average rate of
change in cell-phone use during the following time periods:
(a) 1993–1998 (b) 2002–2004
SOLUTION
(a) Average rate of change
f(19
1
9
9
8
9
)
8
1
f
9
(1
9
9
3
93)
53,20
5
0,000
10,640,000 users/year.
(b) Average rate of change
f(2
2
0
0
0
0
4
4
)
f
2
(
0
2
0
0
2
02)
41,37
2
3,000
20,686,500 users/year. ■
182,140,000 140,767,000
2004 2002
69,209,000 16,009,000
19981993
SECTION 3.6 Rates of Change 207
Year 1993 1994 1995 1996 1997 1998
Millions of 16.009 24.134 33.786 44.043 55.312 69.209
subscribers
Year 1999 2000 2001 2002 2003 2004
Millions of 86.047 109.478 128.375 140.767 158.722 182.140
subscribers

EXAMPLE 4
Figure 3–51 is the graph of the temperature function f during a particular day; f(x)
is the temperature at x hours after midnight. What is the average rate of change of
the temperature (a) from 4 A.M. to noon? (b) from 3 P.M. to 8 P.M.?
Figure 3–51
SOLUTION
(a) The graph shows that the temperature at 4 A.M.isf (4) 40° and the temper-
ature at noon is f (12) 58°. The average rate of change of temperature is
f (1
1
2
2
)
f
4
(4)
5
1
8
2
4
4
0
1
8
8
2.25° per hour.
The rate of change is positive because the temperature is increasing at an
average rate of 2.25° per hour.
(b) Now 3 P.M. corresponds to x 15 and 8 P.M.tox 20. The graph shows that
f (15) 68° and f (20) 53°. Hence, the average rate of change of tempera-
ture is
f (2
2
0
0
)
f
1
(
5
15)
5
2
3
0
6
1
8
5
5
15
3° per hour.
The rate of change is negative because the temperature is decreasing at an
average rate of 3° per hour. ■
GEOMETRIC INTERPRETATION
OF AVERAGE RATE OF CHANGE
If P and Q are points on the graph of a function f, then the straight line determined
by P and Q is called a secant line. Figure 3–52 shows the secant line joining the
points (4, 40) and (12, 58) on the graph of the temperature function f of Example 4.
Change in temperature
Change in time
Change in temperature
Change in time
40°
44°
48°
52°
56°
60°
64°
68°
4812
A.M.
Time of Day
P. M .Noon
16 20 24
Temperature
208 CHAPTER 3 Functions and Graphs
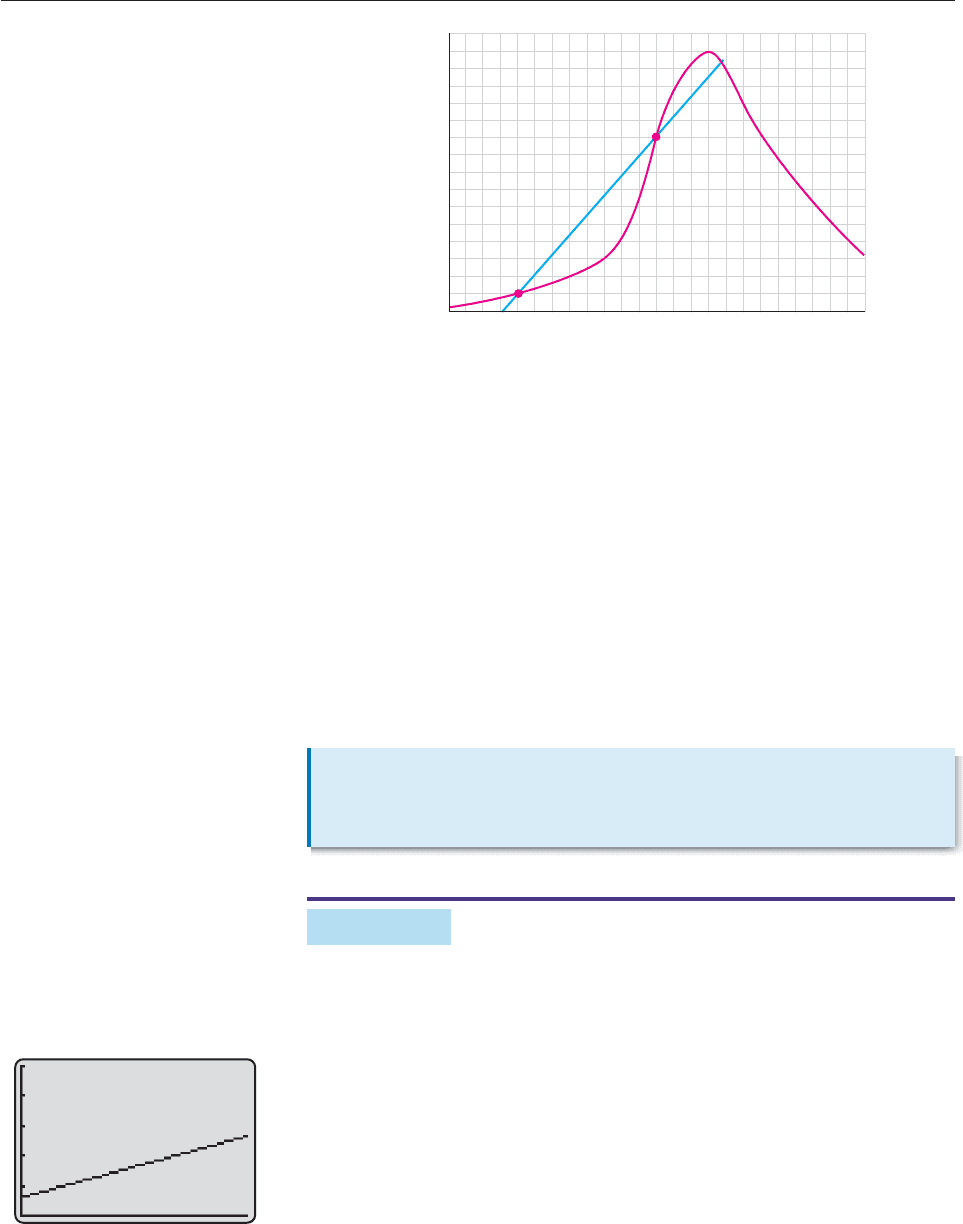
Figure 3–52
Using the points (4, 40) and (12, 58), we see that the slope of this secant line is
5
1
8
2
4
4
0
1
8
8
2.25.
To say that (4, 40) and (12, 58) are on the graph of f means that f (4) 40 and
f (12) 58. Thus,
Slope of secant line 2.25
5
1
8
2
4
4
0
f (1
1
2
2
)
f
4
(4)
Average rate of change as x goes from 4 to 12.
The same thing happens in the general case.
EXAMPLE 5
Assume we have 20 liters of oxygen gas in a thick, unmoving container. The pres-
sure exerted on the walls of the container is a function of the temperature in the
room:
p(T) .00411T 1.1213
where T is in degrees Celsius and p(T) is in atmospheres. So at zero degrees
Celsius (the temperature at which water freezes) the pressure is 1.1213 atmos-
pheres, and at 100 degrees Celsius (the temperature at which water boils) the pres-
sure is 1.5323 atmospheres.
At what average rate does the pressure change as the temperature increases?
SOLUTION The graph of p(T) .00411T 1.1213 is a straight line (Fig-
ure 3–53). So the secant line joining any two points on the graph is just the graph
40
44
48
52
56
60
64
68
4812
A.M.
0
Midnight
Time of Day
P. M .Noon
16 20 24
Temperature
(4, 40)
(12, 58)
SECTION 3.6 Rates of Change 209
Secant Lines and
Average Rates
of Change
If f is a function, then the average rate of change of f (x) with respect to x as
x changes from x a to x b is the slope of the secant line joining the
points (a, f (a)) and (b, f (b)) on the graph of f.
2
100
1
0
Figure 3–53
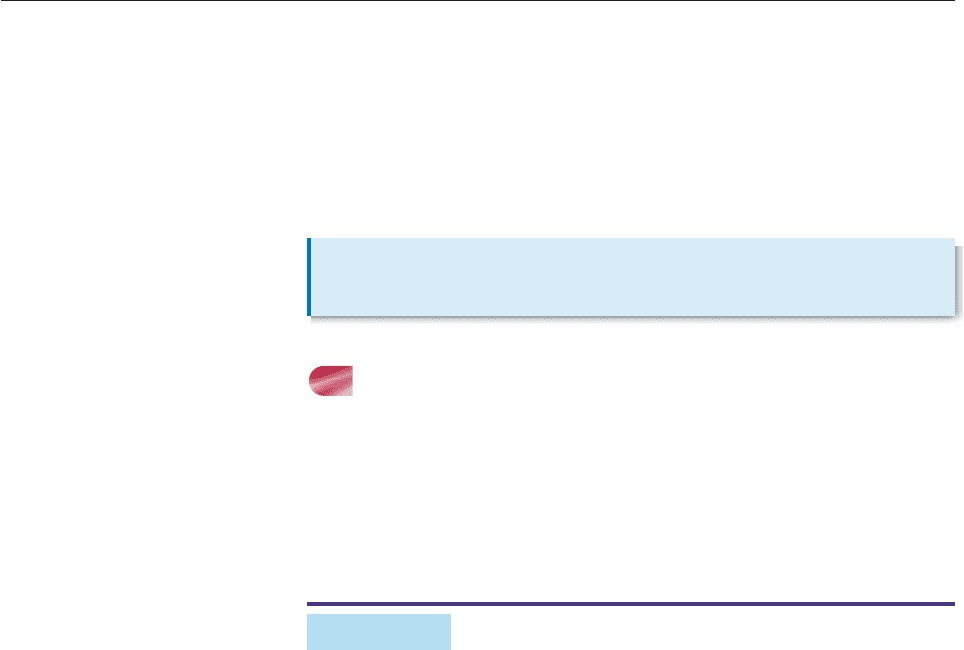
itself, the line y .00411T 1.1213. As we saw in Section 1.4, the slope of this
line is .00411. Therefore, the average rate of change of the pressure function
between any two values of T is .00411. In other words, at any temperature, the
pressure will increase at a rate of .00411 atmospheres per degree. ■
The argument used in Example 5 works for any function whose graph is a
straight line and leads to this conclusion.
THE DIFFERENCE QUOTIENT
Average rates of change are often computed for very small intervals. For instance,
we might compute the rate from 4 to 4.01 or from 4 to 4.001. Since
4.01 4 .01 and 4.001 4 .001, we are doing essentially the same thing in
both cases: computing the rate of change over the interval from 4 to 4 h for
some small nonzero quantity h. Furthermore, it’s often possible to use a single cal-
culation to determine the average rate for all possible values of h.
EXAMPLE 6
Consider the falling rock with which this section began. The distance the rock has
traveled at time t is given by d(t) 16t
2
, and its average speed (rate of change)
from t 4 to t 4 h is
Average speed
d(4
(4
h
h
)
)
d
4
(4)
128h
h
16h
2
h(128
h
16h)
128 16h.
Thus, we can quickly compute the average speed over the interval from 4 to
4 h seconds for any value of h by using the formula
Average speed 128 16h.
For example, the average speed from 4 seconds to 4.001 seconds (here h .001)
is
128 16h 128 16(.001) 128 .016 128.016 feet per second. ■
Similar calculations can be done with any number in place of 4. In each such
case, we are dealing with an interval from x to x h for some number x. As in
Example 6, a single computation can often be used for all possible x and h.
256 128h 16h
2
256
h
16(16 8h h
2
) 256
h
16(4 h)
2
16
4
2
h
210 CHAPTER 3 Functions and Graphs
Rates of Change
of Linear Functions
The average rate of change of a linear function f (x) mx b. as x changes
from one value to another, is the slope m of the line.

EXAMPLE 7
The average speed of the falling rock of Example 6 from time x to time x h is:*
Average speed
d(x
(x
h
h
)
)
d
x
(x)
16(x h
h
)
2
16x
2
32xh
h
16h
2
h(32x
h
16h)
32x 16h.
When x 4, then this result states that the average speed from 4 to 4 h is
32(4) 16h 128 16h, which is exactly what we found in Example 4. To find
the average speed from 3 to 3.1 seconds, apply the formula
Average speed 32x 16h
with x 3 and h .1:
Average speed 32
3 16(.1) 96 1.6 97.6 feet per second. ■
More generally, we can compute the average rate of change of any function f
over the interval from x to x h just as we did in Example 7: Apply the definition
of average rate of change in the box on page 206 with x in place of a and
x h in place of b:
Average rate of change
f(b
b
)
f
a
(a)
f (x
(x
h
h
)
)
f
x
(x)
f (x h
h
) f (x)
.
This last quantity is just the difference quotient of f (see page 154). Therefore,
EXAMPLE 8
Find the difference quotient of V(x) x
3
/55, and use it to find the average rate of
change of V as x changes from 8 to 8.01.
16x
2
32xh 16h
2
16x
2
h
16(x
2
2xh h
2
) 16x
2
h
SECTION 3.6 Rates of Change 211
Difference Quotients and
Rates of Change
If f is a function, then the average rate of change of f over the interval from
x to x h is given by the difference quotient
f (x h
h
) f (x)
.
*Note that this calculation is the same as in Example 6 except that 4 has been replaced by x.

SOLUTION Use the definition of the difference quotient and algebra:
V(x h) V(x)
64748 678
V(x h
h
) V(x)
5
1
5
(x h
h
)
3
x
3
5
1
5
5
1
5
3x
2
h 3
h
xh
2
h
3
5
1
5
h(3x
2
h
3xh h
2
)
3x
2
5
3
5
xh h
2
.
When x changes from 8 to 8.01 8 .01, we have x 8 and h .01. So the
average rate of change is
3x
2
5
3
5
xh h
2
3.495. ■
If you’ve been reading carefully, you might be thinking that this process makes
something simple (computing the average rate of change of a function from x 8
to x 8.01) into something difficult (FIRST computing the average rate of
change from x to x h, using some messy algebra, and then letting x 8 and
h .01). If all we wanted to do was compute one such rate, you would be right.
We usually use this technique when we want to look at the same function for
many values of h, as we will in the next example. We basically are doing an ugly
calculation one time to make a series of future calculations simpler.
INSTANTANEOUS RATE OF CHANGE
Rates of change are a major theme in calculus—not just the average rate of change
discussed above, but also the instantaneous rate of change of a function (that is,
its rate of change at a particular instant). Even without calculus, however, we can
obtain quite accurate approximations of instantaneous rates of change by using
average rates appropriately.
EXAMPLE 9
A rock is dropped from a high place. What is its speed exactly 3 seconds after it is
dropped?
SOLUTION The distance the rock has fallen at time t is given by the function
d(t) 16t
2
. The exact speed at t 3 can be approximated by finding the average
speed over very small time intervals, say, 3 to 3.01 or even shorter intervals. Over
a very short time span, such as a hundredth of a second, the rock cannot change
speed very much, so these average speeds should be a reasonable approximation
of its speed at the instant t 3. Example 7 shows that the average speed is given
3
8
2
3
8(.01) (.01)
2
55
x
3
3x
2
h 3xh
2
h
3
x
3
h
5
1
5
[(x h)
3
x
3
]
h
(x
55
h)
3
5
x
5
3
h
212 CHAPTER 3 Functions and Graphs
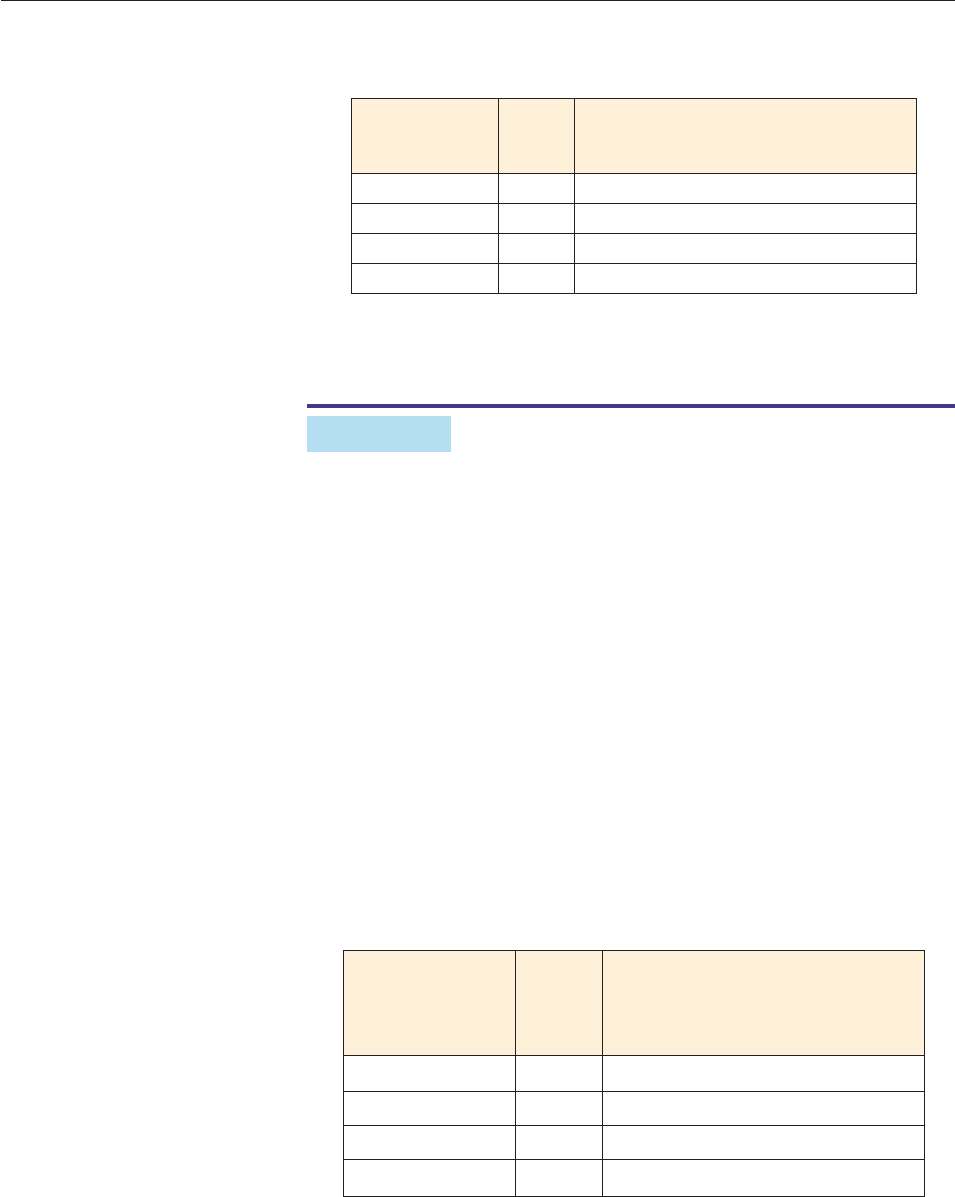
The table suggests that the exact speed of the rock at the instant t 3 seconds is
very close to 96 feet per second. ■
EXAMPLE 10
A balloon is being filled with water in such a way that when its radius is x inches,
then its volume is V(x) x
3
/55 gallons. In Example 2, we saw that the average
rate of change of the volume as the radius increases from 5 inches to 10 inches is
3.182 gallons per inch. What is the rate of change at the instant when the radius is
7 inches?
SOLUTION The average rate of change when the radius goes from x to
x h inches is given by the difference quotient of V(x), which was found in
Example 8:
V(x h
h
) V(x)
3x
2
5
3
5
xh h
2
.
Therefore, when x 7, the difference quotient is
147
5
2
5
1h h
2
,
and we have these average rates of change over small intervals near 7:
The chart suggests that at the instant the radius is 7 inches, the volume is chang-
ing at a rate of approximately 2.673 gallons per inch. ■
3
7
2
3
7
h h
2
55
SECTION 3.6 Rates of Change 213
Average Speed
Change in Time [Difference Quotient at x 3]
3 to 3 hh 96 16h
3 to 3.1 .1 96 16(.1) 97.6 ft per second
3 to 3.01 .01 96 16(.01) 96.16 ft per second
3 to 3.005 .005 96 16(.005) 96.08 ft per second
3 to 3.00001 .00001 96 16(.00001) 96.00016 ft per second
Average Rate of Change of Volume
[Difference Quotient at x 7]
Change in Radius
7 to 7 hh
147
5
2
5
1h h
2
7 to 7.01 .01 2.6765 gallons per inch
7 to 7.001 .001 2.6731 gallons per inch
7 to 7.0001 .0001 2.6728 gallons per inch
7 to 7.00001 .00001 2.6727 gallons per inch
by the difference quotient 32x 16h. When x 3, the difference quotient is
32
3 16h 96 16h, and we have the following:
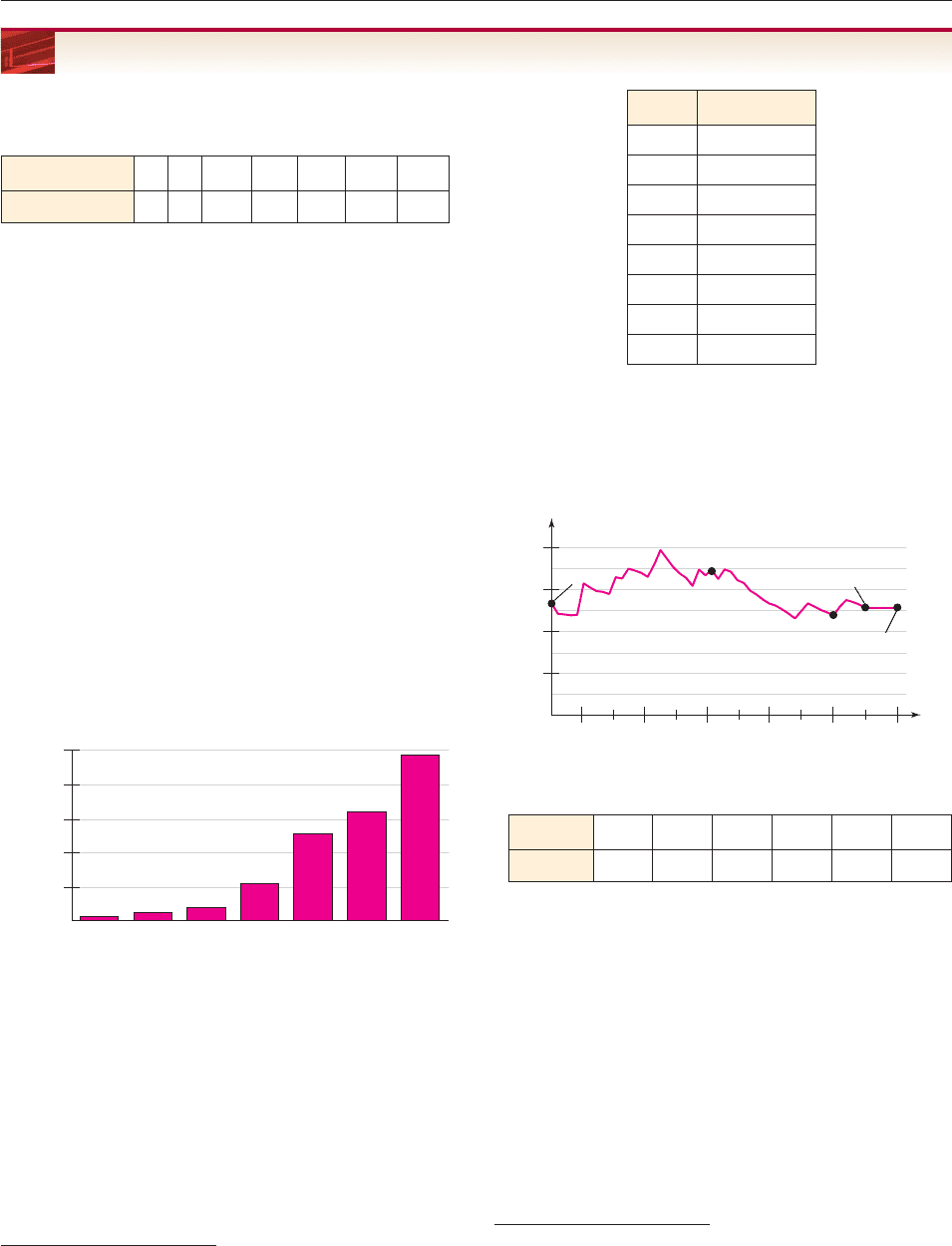
214 CHAPTER 3 Functions and Graphs
EXERCISES 3.6
1. A car moves along a straight test track. The distance trav-
eled by the car at various times is shown in this table:
Find the average speed of the car over the interval from
(a) 0 to 10 seconds (b) 10 to 20 seconds
(c) 20 to 30 seconds (d) 15 to 30 seconds
2. Find the average rate of change of the volume of the balloon
in Example 2 as the radius increases from
(a) 2 to 5 inches (b) 4 to 8 inches
3. Use the function of Example 3 to find the average rate of
change in cell-phone use from
(a) 1994–1996 (b) 1999–2004
4. The graph shows the total amount spent on advertising (in
millions of dollars) in the United States, as estimated by
a leading advertising publication.* Find the average rate of
change in advertising expenditures over the following time
periods:
(a) 1950–1970 (b) 1970–1980
(c) 1980–2000 (d) 1950–2000
(e) During which of these periods were expenditures
increasing at the fastest rate?
5. The following table shows the total projected elementary
and secondary school enrollment (in thousands) for se-
lected years.
†
Find the average rate of change of enrollment
from
(a) 1980 to 1985 (b) 1985 to 1995
(c) 1995 to 2005 (d) 2005 to 2014
(e) During which of these periods was enrollment increas-
ing at the fastest rate? At the slowest rate?
1950
$5,700
1960
$11,960
1970
$19,550
1980
$54,780
1990
$128,640
1995
$160,930
2000
$243,680
250,000
200,000
150,000
100,000
50,000
6. The graph shows the minimum wage (in constant 2000 dol-
lars), with x 0 corresponding to 1950.* Find the average
rate of change in the minimum wage from
(a) 1950 to 1976 (b) 1976 to 1995
(c) 1995 to 2000 (d) 1976 to 2000
7. The table shows the total number of shares traded (in bil-
lions) on the New York Stock Exchange in selected years.
†
Find the average rate of change in share volume from
(a) 1995 to 1999 (b) 1999 to 2001
(c) 2001 to 2005 (d) 1995 to 2005
(e) During which of these periods did share volume
increase at the fastest rate?
8. The graph in the figure
‡
shows the popularity of the name
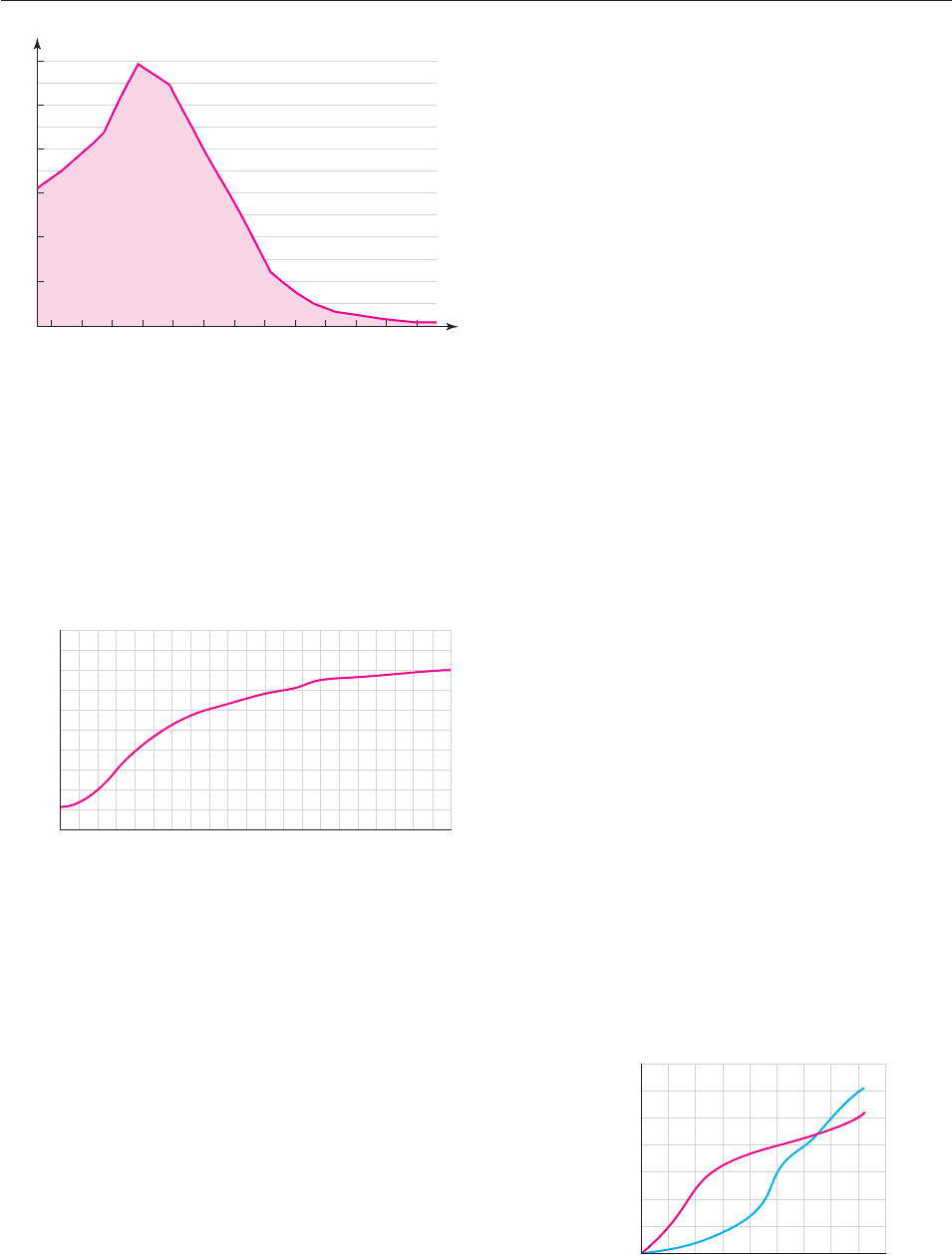
Frances since the 1880s, when records started to be kept. The
y-axis shows the usage of “Frances” per million babies. The
name increased in popularity until the 1910s, and then its
popularity decreased. Estimate the average rate of change of
popularity (in usage per million per year) over the interval:
(a) 1880 to 1890 (b) 1880 to 1930
(c) 1930 to 1950 (d) 1950 to 1990
5 10152025303540455055
x
y
$8
$6
$4
$2
(0, 5.36)
(26, 6.96)
(50, 5.15)
(55, 5.15)
(45, 4.80)
Time (seconds) 0 5 10 15 20 25 30
Distance (feet) 0 20 140 400 680 1400 1800
Year Enrollment
1980 40,877
1985 39,422
1990 41,217
1995 44,840
2000 47,204
2005 48,375
2010 48,842
2014 49,993
*Advertising Age.
†
U.S. National Center for Education Statistics.
Year 1995 1997 1999 2001 2003 2005
Volume 87.2 133.3 203.9 307.5 352.4 403.8
*U.S. Employment Standards Administration.
†
NYSE Factbook.
‡
Baby Name Wizard.
9. The Pennyfarthing Bicycle Company has found that its
sales are related to the amount of advertising it does in trade
magazines. The graph in the figure shows the sales (in thou-
sands of dollars) as a function of the amount of advertising
(in number of magazine ad pages). Find the average rate of
change of sales when the number of ad pages increases from
(a) 10 to 20 (b) 20 to 60
(c) 60 to 100 (d) 0 to 100
(e) Is it worthwhile to buy more than 70 pages of ads, if the
cost of a one-page ad is $2000? If the cost is $5000? If
the cost is $8000?
10. When blood flows through an artery (which can be thought
of as a cylindrical tube) its velocity is greatest at the center
of the artery. Because of friction along the walls of the tube,
the blood’s velocity decreases as the distance r from the
center of the artery increases, finally becoming 0 at the wall
of the artery. The velocity (in centimeters per second) is
given by the function v 18,500(.000065 r
2
), where r is
measured in centimeters. Find the average rate of change of
the velocity as the distance from the center changes from
(a) r .001 to r .002 (b) r .002 to r .003
(c) r 0 to r .005
In Exercises 11–17, find the average rate of change of the func-
tion f over the given interval.
11. f(x) 3 x
3
from x 0 to x 2
12. f(x) .25x
4
x
2
2x 4 from x 1 to x 4
13. f(x) x
3
3x
2
8x 6 from x 1 to x 3
200
100
Sales
605040 90 10080703020100
Pages
5,000
4,000
3,000
2,000
1,000
1880
x
y
1890 1900 1910 1920 1930 1940 1950 1960 1970 1980 1990 2004
6,000
SECTION 3.6 Rates of Change 215
14. f(x) x
4
x
3
2x
2
x
4
from x 0 to x 3
15. f(x)
x
3
2
x
2
6
x 5
from x 1 to x 1.01
16. f(x)
x
3
2
x
2
6
x 5
from x 1 to x 1.00001
17. f(x)
2
x
x
2
3
4
from x 3 to x 8
In Exercises 18–25, compute and simplify the difference
quotient of the function.
18. f(x) x 5 19. f (x) 7x 2
20. f(x) x
2
3 21. f(x) x
2
3x 1
22. f(t) 160,000 8000t t
2
23. V(x) x
3
24. A(r) pr
2
25. V( p) 5/p
26. Water is draining from a large tank. After t minutes, there
are 160,000 8000t t
2
gallons of water in the tank.
(a) Use the results of Exercise 22 to find the average rate at
which the water runs out in the interval from 10 to
10.1 minutes.
(b) Do the same for the interval from 10 to 10.01 minutes.
(c) Estimate the rate at which the water runs out after
exactly 10 minutes.
27. Use the results of Exercise 23 to find the average rate of
change of the volume of a cube whose side has length x as x
changes from
(a) 4 to 4.1 (b) 4 to 4.01 (c) 4 to 4.001
(d) Estimate the rate of change of the volume at the instant
when x 4.
28. Use the results of Exercise 24 to find the average rate of
change of the area of a circle of radius r as r changes from
(a) 4 to 4.5 (b) 4 to 4.2 (c) 4 to 4.1
(d) Estimate the rate of change at the instant when r 4.
(e) How is your answer in part (d) related to the circumfer-
ence of a circle of radius 4?
29. Under certain conditions, the volume V of a quantity of air
is related to the pressure p (which is measured in kilopas-
cals) by the equation V 5/p. Use the results of Exer-
cise 25 to estimate the rate at which the volume is changing
at the instant when the pressure is 50 kilopascals.
30. Two cars race on a straight track, beginning from a dead
stop. The distance (in feet) each car has covered at each
time during the first 16 seconds is shown in the figure.
1200
1000
800
400
600
200
Distance
24681012
D
C
14 16 18
Time
Car C
Car D
